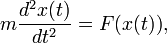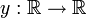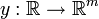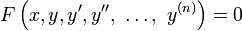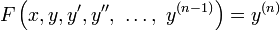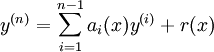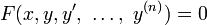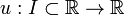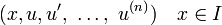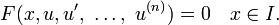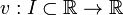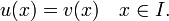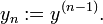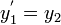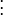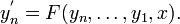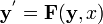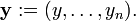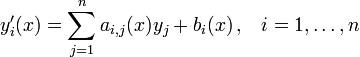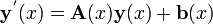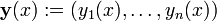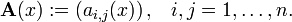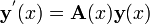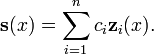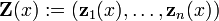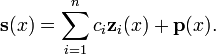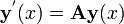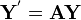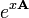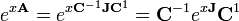??quation diff??rentielle ordinaire

?? propos de ce ??coles s??lection Wikipedia

Ce contenu de Wikipedia a ??t?? s??lectionn?? par SOS Enfants d'aptitude dans les ??coles ?? travers le monde. Parrainer un enfant de faire une r??elle diff??rence.

En math??matiques , une ??quation diff??rentielle ordinaire (ou ODE) est une relation qui contient des fonctions d'un seul variable ind??pendante, et une ou plusieurs de ses d??riv??s par rapport ?? cette variable.

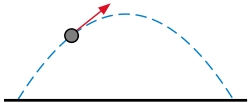
Un exemple simple est la deuxi??me loi de Newton de mouvement, ce qui conduit ?? l'??quation diff??rentielle

$m \ frac {d ^ 2 x (t) dt} {^ 2} = F (x (t)), \,$

pour le mouvement d'une particule de masse m. En g??n??ral, la force F d??pend de la position de la particule x (t) au temps t, et par cons??quent la fonction inconnue x (t) appara??t sur les deux c??t??s de l'??quation diff??rentielle, comme cela est indiqu?? dans la notation F (x (t )).

??quations diff??rentielles ordinaires sont ?? distinguer des ??quations aux d??riv??es partielles o?? il ya plusieurs variables ind??pendantes impliquant d??riv??es partielles.

??quations diff??rentielles ordinaires se posent dans de nombreux contextes diff??rents, y compris la g??om??trie, la m??canique, l'astronomie et la mod??lisation de la population. Beaucoup de math??maticiens c??l??bres ont ??tudi?? ??quations diff??rentielles et a contribu?? sur le terrain, y compris Newton , Leibniz , le Famille Bernoulli, Riccati, Clairaut, d'Alembert et Euler .

Beaucoup d'??tude a ??t?? consacr??e ?? la solution d'??quations diff??rentielles ordinaires. Dans le cas o?? l'??quation est lin??aire, il peut ??tre r??solu par des m??thodes analytiques. Malheureusement, la plupart des ??quations diff??rentielles sont int??ressants non lin??aire et, ?? quelques exceptions pr??s, ne peut ??tre r??solu exactement. Solutions approximatives sont arriv??s ?? l'aide d'approximations de l'ordinateur (voir ??quations diff??rentielles ordinaires num??riques).

Le une trajectoire de projectile lanc?? ?? partir d'un canon suit une courbe d??termin??e par une ??quation diff??rentielle ordinaire qui est d??riv??e de la seconde loi de Newton.

D??finitions

??quation diff??rentielle ordinaire

Soit y une fonction inconnue

$Y: \ mathbb {R} \ to \ mathbb {R}$

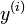en x avec $y ^ {(i)}$ la i i??me d??riv??e de y, puis une fonction

$F (x, y, y ', \ \ dots, \ y ^ {(n-1)}) = {y ^ (n)}$

est appel?? une ??quation diff??rentielle ordinaire (ODE) d'ordre n. Pour fonctions vectorielles valeur

$Y: \ mathbb {R} \ to \ mathbb {R} ^ m$

F est appel?? un syst??me d'??quations diff??rentielles ordinaires de dimension m.

Quand une ??quation diff??rentielle d'ordre n est de la forme

$F \ left (x, y, y ', y' ', \ \ dots, \ y ^ {(n)} \ right) = 0$

il est appel?? une ??quation diff??rentielle implicite alors que la forme

$F \ left (x, y, y ', y' ', \ \ dots, \ y ^ {(n-1)} \ right) = y ^ {(n)}$

est appel?? une ??quation diff??rentielle explicite.

Une ??quation diff??rentielle non en fonction de x est appel??e autonome.

Une ??quation diff??rentielle est dite lin??aire si F peut ??tre ??crit comme une combinaison lin??aire des d??riv??s de y

$^ {y (n)} = \ sum_ {i = 1} ^ {n-1} a_i (x) ^ {y (i)} + r (x)$

avec un _i (x) et R (x) des fonctions continues en x. La fonction r (x) est appel?? le terme source; si r (x) = 0 alors l'??quation diff??rentielle lin??aire est dit homog??ne, sinon il est appel?? non homog??ne ou h??t??rog??ne.

Solutions

Compte tenu d'une ??quation diff??rentielle

$F (x, y, y ', \ \ dots, \ ^ {y (n)}) = 0$

une fonction

$u: Je \ subset \ mathbb {R} \ ?? \ mathbb {R}$

est appel?? solution ou courbe int??grale F, si u est n -Times d??rivable sur I, F est d??fini pour tous

$(X, u, u ', \ \ dots, \ u ^ {(n)}) \ quad x \ in I$

$F (x, u, u ', \ \ dots, \ u ^ {(n)}) = 0 \ quad x \ in I.$

Compte tenu des deux solutions

$u: J \ subset \ mathbb {R} \ ?? \ mathbb {R}$

$v: Je \ subset \ mathbb {R} \ ?? \ mathbb {R}$

u est appel?? une extension de v si je ⊂ J et

$u (x) = v (x) \ quad x \ in I. \,$

Une solution qui n'a pas d'extension se appelle une solution mondiale.

Une solution g??n??rale d'une ??quation d'ordre de n -i??me est une solution contenant $n$ des variables arbitraires, correspondant ?? n constantes d'int??gration. Une solution particuli??re est d??riv?? de la solution g??n??rale en d??finissant les constantes ?? des valeurs particuli??res, souvent choisi pour remplir SET 'conditions initiales ou aux limites ??. Un solution unique est une solution qui ne peut ??tre d??riv?? de la solution g??n??rale.

Exemples

R??duction ?? un premier syst??me de commande

Toute ??quation diff??rentielle d'ordre n peut ??tre ??crit comme un syst??me d'??quations diff??rentielles du premier ordre n. Compte tenu d'une ??quation diff??rentielle ordinaire explicite d'ordre n et une dimension,

$F \ left (x, y, y ', y' ', \ \ dots, \ y ^ {(n-1)} \ right) = y ^ {(n)}$

nous d??finissons une nouvelle famille de fonctions inconnues

$y_n: = y ^ {(n-1)} \.!$

Nous pouvons alors r????crire l'??quation diff??rentielle d'origine comme un syst??me d'??quations diff??rentielles ?? l'ordre 1 et la dimension n.

$y_1 ^ '= Y_2$

$\ vdots$

$y_n ^ '= F (y_n, \ dots, y_1, x).$

qui peut ??tre ??crite de fa??on concise dans la notation de vecteur

$\ Mathbf {y} ^ '= \ mathbf {F} (\ mathbf {y}, x)$

avec

$\ Mathbf {y}: = (y, \ ldots, y_n).$

Lin??aires des ??quations diff??rentielles ordinaires

Une classe particuli??re bien compris des ??quations diff??rentielles sont des ??quations diff??rentielles lin??aires. Nous pouvons toujours r??duire une ??quation explicite diff??rentiel lin??aire de ne importe quel ordre ?? un syst??me d'??quations diff??rentielles d'ordre 1

$y_i '(x) = \ sum_ {j = 1} ^ n a_ {i, j} (x) + y_j b_i (x) \, \ mathrm {,} \ quad i = 1, \ ldots, n$

que nous pouvons ??crire de mani??re concise en utilisant la notation de vecteur

$\ Mathbf {y} ^ '(x) = \ mathbf {A} (x) \ mathbf {y} (x) + \ mathbf {b} (x)$

avec

$\ Mathbf {y} (x): = (y_1 (x), \ ldots, y_n (x))$

$\ Mathbf {b} (x): = (b_1 (x), \ ldots, b_n (x))$

$\ Mathbf {A} (x): = (a_ {i, j} (x)) \, \ mathrm {,} \ quad i, j = 1, \ ldots, n.$

??quations homog??nes

L'ensemble des solutions pour un syst??me d'??quations diff??rentielles lin??aires homog??nes d'ordre 1 et la dimension n

$\ Mathbf {y} ^ '(x) = \ mathbf {A} (x) \ mathbf {y} (x)$

forme un n de dimension espace vectoriel . Compte tenu d'une base de cet espace vectoriel 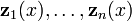$\ Mathbf {z} _1 (x), \ ldots, \ mathbf {z} _n (x)$ , Qui est appel?? un syst??me fondamental, toutes les solutions 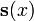$\ Mathbf {s} (x)$ peut se ??crire

$\ Mathbf {s} (x) = \ sum_ {i = 1} ^ {n} c_i \ mathbf {z} _i (x).$

La matrice n ?? n

$\ Mathbf {Z} (x): = (\ mathbf {z} _1 (x), \ ldots, \ mathbf {z} _n (x))$

est appel??e matrice fondamentale. En g??n??ral, il ne existe aucune m??thode pour construire explicitement un syst??me fondamental, mais si une solution est connue r??duction d'Alembert peut ??tre utilis?? pour r??duire la dimension de l'??quation diff??rentielle par un.

??quations non homog??nes

L'ensemble des solutions pour un syst??me d'??quations diff??rentielles lin??aires homog??nes d'ordre 1 et la dimension n

$\ Mathbf {y} ^ '(x) = \ mathbf {A} (x) \ mathbf {y} (x) + \ mathbf {b} (x)$

peut ??tre construite en trouvant le syst??me fondamental 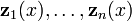$\ Mathbf {z} _1 (x), \ ldots, \ mathbf {z} _n (x)$ ?? l'??quation homog??ne correspondante et une solution particuli??re 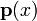$\ Mathbf {p} (x)$ ?? l'??quation inhomog??ne. Chaque solution 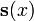$\ Mathbf {s} (x)$ l'??quation inhomog??ne peut alors ??tre ??crite comme

$\ Mathbf {s} (x) = \ sum_ {i = 1} ^ {n} c_i \ mathbf {z} _i (x) + \ mathbf {p} (x).$

Une solution particuli??re de l'??quation inhomog??ne se trouve sous la m??thode des coefficients ind??termin??s ou Proc??d?? de variation de param??tres.

Syst??mes fondamentaux pour les ??quations homog??nes ?? coefficients constants

Pour un syst??me d'??quations diff??rentielles lin??aires homog??nes ?? coefficients constants

$\ Mathbf {y} ^ '(x) = \ mathbf {A} \ mathbf {y} (x)$

nous pouvons explicitement construire un syst??me fondamental. Le syst??me peut ??tre ??crite comme une ??quation diff??rentielle matrice

$\ Mathbf {Y} ^ '= \ mathbf {A} \ mathbf {Y}$

avec une solution comme matrice exponentielle

$e ^ {x \ mathbf {A}}$

qui est une matrice fondamentale de l'??quation diff??rentielle d'origine. Pour calculer explicitement cette expression nous transformons A en premier R??duction de Jordan

$e ^ {x \ mathbf {A}} = e ^ {x \ mathbf {C} ^ {- 1} \ mathbf {J} \ mathbf {C} ^ {1}} = \ mathbf {C} ^ {- 1 } e ^ {x \ mathbf {J}} \ mathbf {C} ^ {1}$

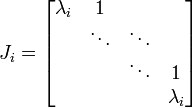
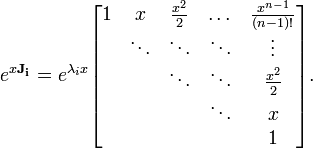
puis ??valuer la Blocs de Jordan

$J_i = \ begin {bmatrix} \ lambda_i & 1 & \; & \; \\ \; & \ & Ddots \ ddots & \; \\ \; & \; & \ & Ddots 1 \\ \; & \; & \; & \ Lambda_i \ end {} bmatrix$

de J s??par??ment en tant que

$e ^ {x \ mathbf {}} J_i = e ^ {\ lambda_i x} \ begin {} bmatrix 1 & x & \ frac {x ^ 2} {2} \ & points et \ frac {x ^ {n-1 }} {(n-1)} \\ \!; & \ & Ddots \ ddots & \ & ddots \ vdots \\ \; & \; & \ Ddots & \ & ddots \ frac {x ^ 2} {2} \\ \; & \; & \; & \ & Ddots x \\ \; & \; & \; & \; & 1 \ end {} bmatrix.$

Th??ories de EDO

Solutions singuli??res

La th??orie de la solutions singuli??res des ??quations diff??rentielles ordinaires et partielles ??tait un sujet de recherche ?? partir du moment de Leibniz, mais seulement depuis le milieu du XIXe si??cle at-elle re??oivent une attention particuli??re. Un travail pr??cieux, mais peu connu sur le sujet est celle de Houtain (1854). Darboux (?? partir de 1873) ??tait un chef de file dans la th??orie et dans l'interpr??tation g??om??trique de ces solutions, il a ouvert un champ qui a ??t?? travaill?? par divers auteurs, notamment Casorati et Cayley. Pour ce dernier est due (1872) la th??orie de solutions singuli??res des ??quations diff??rentielles du premier ordre comme accept??e vers 1900.

R??duction ?? quadratures

La tentative primitive dans le traitement des ??quations diff??rentielles avait en vue une r??duction quadratures. Comme il avait ??t?? l'espoir de alg??bristes du XVIIIe si??cle pour trouver une m??thode pour r??soudre l'??quation g??n??rale de la $n$ e degr??, donc ce ??tait l'espoir d'analystes de trouver une m??thode g??n??rale pour l'int??gration de toute ??quation diff??rentielle. Gauss (1799) a montr??, cependant, que l'??quation diff??rentielle rencontre ses limites tr??s bient??t moins nombres complexes sont introduits. D'o?? les analystes ont commenc?? ?? remplacer l'??tude des fonctions, ouvrant ainsi un champ nouveau et fertile. Cauchy ??tait le premier ?? appr??cier l'importance de ce point de vue. Par la suite, la v??ritable question ??tait d'??tre, pas si une solution est possible au moyen de fonctions connues ou leurs int??grales, mais de savoir si une ??quation diff??rentielle donn??e suffit pour la d??finition d'une fonction de la variable ind??pendante ou des variables, et si oui, quelles sont les propri??t??s caract??ristiques de cette fonction.

Th??orie fuchsien

Deux m??moires par Fuchs (Crelle, 1866, 1868), a inspir?? une nouvelle approche, par la suite ??labor?? par Thom?? et Frobenius. Collet a ??t?? un contributeur de premier plan ?? partir de 1869, bien que sa m??thode d'int??gration d'un syst??me non-lin??aire a ??t?? communiqu??e ?? Bertrand en 1868. Clebsch (1873) a attaqu?? la th??orie long de lignes parall??les ?? celles suivies dans sa th??orie de Int??grales ab??liennes. Comme celui-ci peuvent ??tre class??s en fonction des propri??t??s de la courbe fondamentale qui reste inchang?? par une transformation rationnelle, afin de Clebsch propos?? de classer les fonctions transcendantes d??finies par les ??quations diff??rentielles selon les propri??t??s invariantes des surfaces correspondantes F = 0 sous rationnelle une -??-une transformations.

La th??orie de Lie

De 1870 Le travail de Lie mis la th??orie des ??quations diff??rentielles sur une base plus satisfaisante. Il a montr?? que les th??ories de l'int??gration des math??maticiens ??g??s peuvent, par l'introduction de ce qu'on appelle aujourd'hui groupes de Lie, ??tre soumis ?? une source commune; et que les ??quations diff??rentielles ordinaires qui admettent m??me transformations infinit??simales pr??sentent des difficult??s d'int??gration comparables. Il a ??galement soulign?? l'objet de transformations de contact (Ber??hrungstransformationen).

Th??orie de Sturm-Liouville

Th??orie de Sturm-Liouville est une m??thode g??n??rale pour la r??solution des ??quations du second ordre lin??aires ?? coefficients variables.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Ordinary_differential_equation&oldid=198824413 "