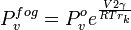La tension de surface

Sujets connexes: Science des mat??riaux ; Physique

Renseignements g??n??raux

Cette s??lection ??coles a ??t?? choisi par SOS Enfants pour les ??coles dans le monde en d??veloppement ne ont pas acc??s ?? Internet. Il est disponible en t??l??chargement intranet. SOS Enfants a regard?? des enfants en Afrique depuis quarante ans. Pouvez-vous aider dans leur travail en Afrique ?

M??canique des milieux continus

Lois Conservation de la masse Conservation du moment Conservation de l'??nergie Entropy in??galit??s
M??canique des solides Solides Stress D??formation Compatibilit?? D??formation finie Souche infinit??simale ??lasticit?? lin??aire Plasticit?? Fl??chissement La loi de Hooke La th??orie de la d??faillance des mat??riaux M??canique de la rupture M??canique du contact Friction Frictionnel
M??canique des fluides Fluides Statique des fluides La dynamique des fluides ??quations de Navier-Stokes Le principe de Bernoulli Flottabilit?? Viscosit?? Newtonien Non-Newtonian Le principe d'Archim??de La loi de Pascal Pression Liquides La tension de surface L'action capillaire Gaz Atmosph??re La loi de Boyle Loi de Charles Loi de Gay-Lussac Loi des gaz combin??e Plasma
Rh??ologie Visco??lasticit?? Fluides intelligents Magnetorheological ??lectrorh??ologique Ferrofluides Rh??om??trie Rh??om??tre
Les scientifiques Bernoulli Boyle Cauchy Charles Euler Gay-Lussac Hooke Pascal Newton Navier Stokes

La tension superficielle est une propri??t?? de la surface d'un liquide qui l'am??ne ?? se comporter comme un feuille ??lastique. Il permet insectes , tels que la araign??e d'eau (??tang de patineur, Royaume-Uni ), de marcher sur l'eau . Il permet de petits objets, m??me m??talliques, tels que des aiguilles, des lames de rasoir, ou des fragments de feuilles, de flotter ?? la surface de l'eau, et elle est la cause de l'action capillaire.

Le comportement physique et chimique des liquides ne peut ??tre comprise sans prendre la tension de surface en compte. Elle r??git la forme que de petites masses de liquide peuvent assumer et le degr?? de contact d'un liquide peut faire avec une autre substance.

Application de la physique newtonienne aux forces qui se posent en raison de la tension de surface pr??dit avec pr??cision de nombreux comportements liquides, qui sont tellement banal que la plupart des gens prennent pour acquis. Application de la thermodynamique ?? ces m??mes forces pr??dit en outre d'autres comportements liquides plus subtiles.

Cause

Diagramme des forces sur une mol??cule de liquide.

La tension de surface est provoqu??e par l'attraction entre les mol??cules du liquide par diverses des forces intermol??culaires. Dans la majeure partie du liquide est tir?? chaque mol??cule dans toutes les directions par les mol??cules liquides voisine, r??sultant en une force nette de z??ro. A la surface du liquide, les mol??cules sont tir??s vers l'int??rieur par d'autres mol??cules plus profondes ?? l'int??rieur du liquide et ne sont pas attir??s par le plus intens??ment les mol??cules dans le milieu voisin (que ce soit sous vide, de l'air ou un autre liquide). Par cons??quent, la totalit?? des mol??cules ?? la surface sont soumises ?? une force vers l'int??rieur de l'attraction mol??culaire qui peuvent ??tre en ??quilibre que par la r??sistance du liquide de compression. Cette traction vers l'int??rieur tend ?? diminuer l'aire de surface, et ?? cet ??gard une surface liquide ressemble ?? une membrane ??lastique ??tir??. Ainsi, le liquide lui-m??me comprime ensemble jusqu'?? ce qu'il a le plus bas Superficie localement possible de surface.

Une autre fa??on de voir cela est que la mol??cule en contact avec un voisin est dans un ??tat d'??nergie plus faible que si elle ne ??tait pas en contact avec un voisin. Les mol??cules d'int??rieur ont tous comme de nombreux voisins, car ils peuvent avoir. Mais les mol??cules limites ont moins de voisins que de mol??cules int??rieures et sont donc dans un ??tat d'??nergie sup??rieure. Pour minimiser le liquide ?? son ??tat d'??nergie, il faut minimiser le nombre de mol??cules limites et doit donc minimiser sa surface.

?? la suite de surface minimisation, une surface assumera la forme lisse, il peut (preuve math??matique que les formes "lisses" minimiser surface repose sur l'utilisation de la Euler-Lagrange ??quation). Depuis toute courbure dans les r??sultats de forme de surface de grande r??gion, une ??nergie plus ??lev??e entra??nera ??galement. En cons??quence, la surface sera repousser contre toute courbure dans la m??me mani??re comme une boule pouss??e en mont??e va repousser ?? minimiser son ??nergie potentielle gravitationnelle.

Effets de la vie quotidienne

perles d'eau sur une feuille

chute d'eau du robinet

Quelques exemples des effets de la tension de surface vu l'eau ordinaire:

Perles d'eau de pluie sur la surface d'une automobile cir??. Eau adh??re faiblement ?? la cire et fortement ?? lui-m??me, de sorte clusters d'eau en gouttes. La tension de surface leur donne leur forme quasi-sph??rique, parce que une sph??re a la plus petite surface possible par rapport au volume.

Formation de gouttes se produit quand une masse de liquide est ??tir??e. L'animation montre adh??rente de l'eau ?? la masse du robinet gagner ce qu'il soit tendu ?? un point o?? la tension de surface ne peuvent plus se lient au robinet. On s??pare alors la tension de surface et la chute en forme d'une sph??re. Si un courant d'eau ont ??t?? en cours d'ex??cution du robinet, le flux se briserait en gouttes lors de sa chute. Gravity ??tend le flux, puis la tension superficielle pince en sph??res.

Flottaison des objets plus denses que l'eau se produit lorsque l'objet est non mouillable et son poids est assez petit pour ??tre n?? par les forces r??sultant de la tension de surface.

La s??paration de l'huile et de l'eau est provoqu??e par une tension dans la surface entre les liquides dissemblables. Ce type de tension de surface va par le nom ??tension d'interface??, mais ses physique sont les m??mes.

Larmes de vin est la formation de gouttes et des ruisseaux sur le c??t?? d'un verre contenant une boisson alcoolis??e. Sa cause est une interaction complexe entre les tensions de surface diff??rentes de l'eau et de l'??thanol .

La tension de surface est visible dans d'autres ph??nom??nes commune, surtout quand certaines substances, tensioactifs, sont utilis??s pour diminuer:

Les bulles de savon ont de tr??s grandes surfaces avec tr??s peu en vrac. Bulles dans l'eau pure sont instables. L'utilisation d'agents tensio-actifs, bien que, indroducir un effet de stabilisation ?? bulle (voir Effet Marangoni). Notez que les agents tensio-actifs r??duisent effectivement la tension superficielle de l'eau par un facteur de trois ou plus.

Les emulsions sont d'un type de solution dans laquelle la tension de surface joue un r??le. De minuscules fragments d'huile en suspension dans l'eau pure spontan??ment se assembler en beaucoup plus grandes masses. Mais la pr??sence d'un agent tensio-actif fournit une diminution de la tension superficielle, ce qui permet la stabilit?? de gouttelettes d'huile minutes dans la masse d'eau (ou vice versa).

La physique de base

Deux d??finitions

Sch??ma spectacles, dans crossection, une aiguille flottant ?? la surface de l'eau. Son poids, $\ Scriptstyle f_w$ , Appuie sur la surface, et qui est ??quilibr??e par les forces de tension de surface de chaque c??t??, $\ f_s de scriptstyle$ , Qui sont chacune parall??le ?? la surface de l'eau au niveau des points o?? elle contacte l'aiguille. Notez que les composantes horizontales des deux $\ f_s de scriptstyle$ fl??ches pointent dans des directions oppos??es, de sorte qu'ils se annulent l'un l'autre, mais les composantes verticales pointent dans la m??me direction et donc ajouter jusqu'?? ??quilibrer $\ Scriptstyle f_w$ .

La tension de surface, repr??sent??e par le symbole σ, γ ou T, est d??finie comme la force le long d'une ligne de longueur unitaire, o?? la force est parall??le ?? la surface, mais perpendiculaire ?? la ligne. Une fa??on de cette image est d'imaginer un film de savon plat d??limit??e d'un c??t?? par un fil tendu de la longueur, L. Le fil sera tir?? vers l'int??rieur du film par une force ??gale ?? 2γL (le facteur 2 est parce que le film de savon a deux c??t??s par cons??quent deux surfaces). La tension de surface est donc mesur??e en forces par unit?? de longueur. Son Unit?? SI est newton par m??tre mais la unit?? CGS de dynes par cm est le plus couramment utilis??.

Une d??finition ??quivalente, qui est utile dans la thermodynamique , est le travail effectu?? par unit?? de surface. En tant que tels, afin d'augmenter la zone de surface d'une masse de liquide d'une quantit??, delta A, une quantit?? de travail, γδA, est n??cessaire. Ce travail est stock??e sous forme d'??nergie potentielle. Par cons??quent la tension superficielle peut ??tre ??galement mesur??e en tant que syst??me SI joules par m??tre ² et dans la syst??me CGS que ergs par cm ^2. Comme les syst??mes m??caniques essaient de trouver un ??tat d'??nergie potentielle minimale, une goutte de liquide libre suppose naturellement une forme sph??rique, qui a la surface minimale pour un volume donn??.

L'??quivalence de mesure de l'??nergie par unit?? de surface ?? la force par unit?? de longueur peut ??tre prouv??e par analyse dimensionnelle.

araign??es d'eau

araign??es d'eau ?? l'aide de la tension de surface de l'eau lors de l'accouplement.

Les spectacles de photographie araign??es d'eau debout sur la surface d'un ??tang. Il est clairement visible que les pieds provoquent des indentations dans la surface de l'eau. Et il est intuitivement ??vident que la surface d'indentations a une plus grande surface d'une surface plane. Si la tension de surface tend ?? minimiser la surface, comment est-il que les araign??es d'eau augmentent la surface?

Rappelons que ce que la nature essaie vraiment de minimiser est l'??nergie potentielle. En augmentant l'aire de surface de l'eau, les araign??es d'eau ont augment?? l'??nergie potentielle de cette surface. Mais notez aussi que le centre de masse les araign??es d'eau de est inf??rieur ?? ce qu'il serait si elles ??taient debout sur une surface plane. Ainsi, leur ??nergie potentielle est diminu??e. En effet, lorsque vous combinez les deux effets, l'??nergie potentielle nette est r??duite au minimum. Si les araign??es d'eau d??prim??s la surface plus, l'??nergie de surface accrue serait plus annuler l'??nergie a diminu?? d'abaisser le centre de la masse des insectes. Se ils d??prim??s la surface pas moins, leur centre sup??rieur de la masse serait plus annuler la r??duction de l'??nergie de surface.

La photo des araign??es d'eau illustre ??galement la notion de tension superficielle ??tant comme avoir un film ??lastique sur la surface du liquide. Dans les d??pressions de surface ?? leurs pieds, il est facile de voir que la r??action de ce film ??lastique imagin?? est exactement la lutte contre le poids des insectes.

Courbure et la pression de surface

les forces de tension de surface agissant sur un minuscule (diff??rentiel) parcelle de surface. δθ _x et δθ _y indique le montant des penchent sur les dimensions de la pi??ce. L'??quilibre des forces de traction avec le conduit ?? pression Pression de Laplace

Si aucune force agit normale ?? une surface tendue, la surface doit rester plat. Mais si la pression sur un c??t?? de la surface est diff??rente de la pression sur l'autre c??t??, les r??sultats diff??rence de pression dans la r??gion de temps de surface d'une force normale. Pour que les forces de tension de surface pour annuler la force due ?? la pression, la surface doit ??tre courb??. Le diagramme montre comment courbure de la surface d'un petit morceau de surface conduit ?? une nette composante de forces de tension superficielle agissant perpendiculairement ?? l'axe de la pi??ce. Lorsque toutes les forces sont ??quilibr??es, l'??quation r??sultante est connue sous le nom ??quation de Young-Laplace:

$\ Delta P \ = \ \ gamma \ gauche (\ frac {1} {} R_x + \ frac {1} {} R_y \ right)$

o??:

Δ P est la diff??rence de pression.
γ est la tension superficielle.
R _x et R _y sont des rayons de courbure dans chacun des axes qui sont parall??les ?? la surface.

Solutions ?? cette ??quation d??terminent la forme de gouttes d'eau, flaques d'eau, m??nisques, bulles de savon, et toutes les autres formes d??termin??es par la tension de surface (comme la forme des impressions que les pieds d'une araign??e d'eau font sur la surface d'un ??tang).

Le tableau ci-dessous montre comment la pression interne d'une goutte d'eau augmente avec la diminution de rayon. Pour pas tr??s petites gouttes l'effet est subtil, mais la diff??rence de pression devient ??norme quand les tailles de gouttes se approchent de la taille mol??culaire.

Δ P de gouttes d'eau ?? des rayons diff??rents STP
Rayon Droplet	1 mm	0,1 mm	1 um	10 nm
Δ P ( atm)	0,0014	0,0144	1,436	143,6

Surface du liquide comme un ordinateur

Surface minimale

Pour trouver la forme de la surface minimale d??limit??e par un certain cadre de forme arbitraire en utilisant des moyens strictement math??matiques peut ??tre une t??che intimidante. Pourtant, en fa??onnant le cadre de fil m??tallique et en le plongeant dans le savon-solution, une surface d'environ minimale (exacte en l'absence de gravit??) appara??tra dans le soap-film r??sultant en quelques secondes. Sans un seul calcul, le savon-film arrive ?? une solution d'une ??quation complexe de minimisation de sa propre.

La raison en est que la diff??rence de pression ?? travers une interface de fluide est proportionnelle ?? la courbure moyenne, comme on le voit dans le ??quation de Young-Laplace. Pour un film de savon ouverte, la diff??rence de pression est ??gale ?? z??ro, d'o?? la courbure moyenne est ??gale ?? z??ro, et les surfaces minimales ont la propri??t?? de courbure moyenne nulle.

Les angles de contact

??tant donn?? qu'aucun liquide ne peut exister dans un vide parfait, la surface de tout liquide est une interface entre ce liquide et un autre milieu. La surface sup??rieure d'un bassin, par exemple, est une interface entre l'eau du bassin et l'air. La tension de surface est donc pas une propri??t?? du liquide seul, mais une propri??t?? de l'interface du liquide avec un autre support. Si un liquide est dans un conteneur, puis en dehors de l'interface liquide / air, lors de sa surface sup??rieure, il existe ??galement une interface entre le liquide et les parois du r??cipient. La tension superficielle entre le liquide et l'air est g??n??ralement diff??rent (sup??rieur ??) sa tension de surface avec les parois du r??cipient. Et o?? les deux surfaces se rencontrent, leur g??om??trie doit ??tre telle que l'??quilibre des forces tous.

Forces au point de contact indiqu??s pour l'angle de contact sup??rieur ?? 90 ?? (gauche) et moins de 90 ?? (?? droite)

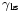Lorsque les deux surfaces se rencontrent, ils forment un angle de contact, $\ Scriptstyle \ theta$ Qui est l'angle de la tangente ?? la surface fait avec la surface solide. Le sch??ma de droite montre deux exemples. L'exemple de la gauche o?? la tension de surface liquide-solide est, $\ Scriptstyle \ gamma _ {\ mathrm {ls}}$ , Est inf??rieure ?? la tension de surface liquide-air, 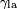$\ Scriptstyle \ gamma _ {\ mathrm {la}}$ , Mais est n??anmoins positive, ce est

$\ Gamma _ {\ mathrm {la}} \> \ \ gamma _ {\ mathrm {ls}} \> \ 0$

Dans le diagramme, les deux forces verticales et horizontales doivent annuler exactement au point de contact. La composante horizontale de $\ Scriptstyle f_ \ mathrm {la}$ est annul??e par la force d'adh??rence, $\ Scriptstyle f_ \ mathrm {A}$ .

$f_ \ mathrm {A} \ = \ f_ \ mathrm {la} \ sin \ theta$

L'??quilibre des forces plus r??v??lateur, cependant, ce est dans le sens vertical. La composante verticale de $\ Scriptstyle f_ \ mathrm {la}$ doit exactement annuler la force, $\ Scriptstyle f_ \ mathrm {ls}$ .

$f_ \ mathrm {ls} \ = \ -f_ \ mathrm {la} \ cos \ theta$

Liquide

Solide

L'angle de contact

eau

verre sodocalcique

verre au plomb

quartz fondu

0 ??

??thanol

l'??ther di??thylique

le t??trachlorure de carbone

glyc??rol

acide ac??tique

eau

paraffine

107 ??

argent

90 ??

l'iodure de m??thyle

verre sodocalcique

29 ??

verre au plomb

30 ??

quartz fondu

33 ??

mercure

verre sodocalcique

140 ??

Certains angles de contact liquide-solide

??tant donn?? que les forces sont en proportion directe avec leurs tensions superficielles respectives, nous avons ??galement:

$\ Gamma_ \ mathrm {ls} \ = \ - \ gamma_ \ mathrm {la} \ cos \ theta$

o??

$\ scriptstyle \ gamma_ \ mathrm {ls}$ est la tension de surface liquide-solide,
$\ Scriptstyle \ gamma_ \ mathrm {la}$ est la tension de surface liquide-air,
$\ Scriptstyle \ theta$ est l'angle de contact, o?? une partie concave m??nisque a angle de contact inf??rieur ?? 90 ?? et une forme convexe m??nisque a angle sup??rieur ?? 90 ?? de contact.

Cela signifie que, bien que la tension de surface liquide-solide, $\ scriptstyle \ gamma_ \ mathrm {ls}$ , Est difficile ?? mesurer directement, il peut ??tre d??duit de l'angle de contact facile ?? mesurer, $\ Scriptstyle \ theta$ Si la tension de surface liquide-air, $\ Scriptstyle \ gamma_ \ mathrm {la}$ , Est connu.

Cette m??me relation existe dans le diagramme sur la droite. Mais dans ce cas, nous voyons que, parce que l'angle de contact est inf??rieur ?? 90 ??, la tension liquide / surface solide doit ??tre n??gative:

$\ gamma_ \ mathrm {la} \> \ 0 \> \ \ gamma_ \ mathrm {ls}$

Angles de contact sp??ciales

Remarquez que dans le cas particulier d'une interface eau-argent o?? l'angle de contact est ??gale ?? 90 ??, la tension de surface liquide-solide est exactement z??ro. Il est difficile de nettoyer le sol si des liquides avec d??versements angle ≈ 0 ?? de contact, comme l'essence, le k??ros??ne, le benz??ne, etc.

Un autre cas particulier est l'endroit o?? l'angle de contact est exactement 180 ??. Avec de l'eau sp??cialement pr??par?? Teflon?? aborde cette. angle de 180 ?? de contact se produit lorsque la tension de surface liquide-solide est exactement ??gale ?? la tension de surface liquide-air.

$\ Gamma _ {\ mathrm {la}} \ = \ \ gamma _ {\ mathrm {ls}} \> \ 0 \ qquad \ theta \ = \ 180 ^ \ circ$

M??thodes de mesure

Parce que la tension de surface se manifeste dans divers effets, il offre un certain nombre de chemins ?? sa mesure. Lequel proc??d?? est optimum d??pend de la nature du liquide ?? mesurer, les conditions dans lesquelles la tension doit ??tre mesur??e, et la stabilit?? de sa surface quand il est d??form??.

Du m??thode No??y Anneau: La m??thode traditionnelle utilis??e pour mesurer surface ou tension interfaciale. Propri??t??s de mouillage de la surface ou l'interface ont peu d'influence sur cette technique de mesure. Traction maximale exerc??e sur le noyau par la surface est mesur??e.

Une version miniaturis??e de Du No??y m??thode utilise un petit diam??tre aiguille m??tallique ?? la place d'un cycle, en combinaison avec une microbalance ?? haute sensibilit?? pour enregistrer traction maximale. L'avantage de cette m??thode est que les volumes d'??chantillon tr??s petit (en bas ?? quelques dizaines de microlitres) peuvent ??tre mesur??es avec une tr??s grande pr??cision, sans qu'il soit n??cessaire de corriger la flottabilit?? (pour une aiguille ou plut??t, une tige, avec une g??om??trie correcte). En outre, la mesure peut ??tre effectu??e tr??s rapidement et tr??s peu en environ 20 secondes. Premi??res tensiom??tres multicanaux commerciales [CMCeeker] ont r??cemment ??t?? construites sur la base de ce principe.

Wilhelmy m??thode de la plaque: Une m??thode universelle particuli??rement adapt?? pour v??rifier la tension de surface sur des intervalles de temps longues. Une plaque verticale du p??rim??tre connu est fix?? ?? un ??quilibre, et la force due ?? l'humidit?? est mesur??e.

M??thode de la goutte Spinning: Cette technique est id??ale pour mesurer de faibles tensions interfaciales. Le diam??tre d'une goutte dans une phase lourde est mesur??e alors que les deux sont entra??n??s en rotation.

Proc??d?? de d??p??t de la marine militaire: tension superficielle et interfaciale peut ??tre mesur??e par cette technique, m??me ?? des temp??ratures et pressions ??lev??es. G??om??trie d'une goutte est analys?? optiquement. Pour plus de d??tails, voir DROP.

La tension superficielle peut ??tre mesur??e en utilisant la m??thode de la goutte pendante sur une goniom??tre.

Proc??d?? de bulle ?? la pression (m??thode de Jaeger): une technique de mesure pour d??terminer la tension de surface ?? de courtes ??ges de surface. Pression maximale de chaque bulle est mesur??e.

Proc??d?? de d??poser volume: Proc??d?? de d??termination de la tension interfaciale en fonction de l'??ge de l'interface. Une densit?? de liquide est pomp?? dans un second liquide d'une densit?? diff??rente et le temps entre les gouttes produites est mesur??.

Proc??d?? de mont??e capillaire: L'extr??mit?? d'un capillaire est immerg?? dans la solution. La hauteur ?? laquelle la solution arrive ?? l'int??rieur du capillaire est li?? ?? la tension de surface par l'??quation discut?? ci-dessous .

Loi de Tate: Proc??d?? de lecture de pond??ration et une goutte de liquide.

M??thode de la goutte sessile: Proc??d?? de d??termination de la tension superficielle et la densit?? en pla??ant une goutte sur un substrat et en mesurant la l'angle de contact (voir Technique de la goutte sessile).

Effets

Liquide dans un tube vertical

Sch??ma d'un Barom??tre Mercury

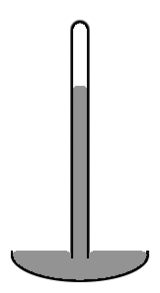
Un vieux style mercure barom??tre se compose d'un tube de verre vertical d'environ 1 cm de diam??tre partiellement remplis avec du mercure, et avec un vide (appel?? le vide de Torricelli) dans le volume vacants (voir sch??ma ci-contre). Notez que le niveau de mercure dans le centre du tube est plus ??lev??e que sur les bords, ce qui rend la face sup??rieure du mercure en forme de d??me. Le centre de masse de l'ensemble de colonne de mercure serait l??g??rement plus faible si la surface sup??rieure du mercure ??tait plat sur toute la crossection du tube. Mais la partie sup??rieure en forme de d??me donne un peu moins de surface pour la totalit?? de la masse de mercure. L?? encore, les deux effets se combinent pour minimiser l'??nergie potentielle totale. Une telle forme de la surface est connu comme un convexe m??nisque.

La raison pour laquelle on consid??re la surface de toute la masse de mercure, y compris la partie de la surface qui est en contact avec le verre, ce est parce que le mercure ne adh??re pas du tout de verre. Ainsi, la tension de surface du mercure agit sur sa surface enti??re, y compris lorsqu'elle est en contact avec le verre. Si au lieu de verre, le tube a ??t?? faite de cuivre, la situation serait tr??s diff??rente. Mercury adh??re agressivement au cuivre. Ainsi, dans un tube de cuivre, le niveau de mercure dans le centre du tube sera plus faible plut??t que plus ??lev??e que sur les bords (ce est-il serait un m??nisque concave). Dans une situation o?? le liquide adh??re aux parois de son conteneur, on consid??re la partie de la surface du fluide qui est en contact avec le r??cipient ?? avoir une tension de surface n??gative. Le fluide fonctionne alors de maximiser la surface de contact. Donc dans ce cas augmenter la surface en contact avec les conteneurs diminue plut??t que augmente l'??nergie potentielle. Cette diminution est suffisant pour compenser l'augmentation de l'??nergie potentielle associ??e ?? la lev??e du fluide ?? proximit?? des parois du r??cipient.

Illustration de mont??e capillaire et ?? l'automne. Rouge = angle de contact inf??rieur ?? 90 ??; bleu = angle sup??rieur ?? 90 ?? de contact

Si un tube est suffisamment ??troite et l'adh??rence du liquide ?? ses parois est suffisamment forte, la tension superficielle peut aspirer du liquide dans le tube ?? un ph??nom??ne connu sous le nom l'action capillaire. La hauteur de la colonne est lev??e ?? est donn?? par:

$h \ = \ \ frac {2 \ gamma_ \ mathrm {la} \ cos \ theta} {\ rho gr}$

o??

$\ Scriptstyle h$ est la hauteur du liquide est soulev??,
$\ Scriptstyle \ gamma_ \ mathrm {la}$ est la tension de surface liquide-air,
$\ Scriptstyle \ rho$ est la masse volumique du liquide,
$\ Scriptstyle r$ est le rayon du capillaire,
$\ Scriptstyle g$ est l'acc??l??ration due ?? la gravit??,
$\ Scriptstyle \ theta$ est l'angle de contact d??crite ci-dessus. Notez que si $\ Scriptstyle \ theta$ est sup??rieur ?? 90 ??, comme le mercure dans un r??cipient en verre, le liquide va ??tre enfonc??e au lieu de lev??e.

Flaques sur une surface

Profil de courbe le bord d'une flaque d'eau o?? l'angle de contact est de 180 ??. La courbe est donn??e par la formule: $\ Scriptstyle x - x_0 \ = \ \ frac {1} {2} H \ cosh ^ {- 1} \ left (\ frac {H} {h} \ right) - H \ sqrt {1 - \ frac {h ^ 2} {H ^ 2}}$ o?? $\ Scriptstyle H \ = \ 2 \ sqrt {\ frac {\ gamma} {g \ rho}}$

Petites flaques d'eau sur une surface propre et lisse ont une ??paisseur perceptible.

Verser le mercure sur une feuille plane horizontale des r??sultats de verre dans un flaque d'eau qui a une ??paisseur perceptible (ne essayez pas cela, sauf en vertu d'un hotte de fum??e. La vapeur de mercure est un risque de toxicit??). La flaque d'eau se propage uniquement au point o?? ce est un peu moins d'un demi-centim??tre d'??paisseur, et pas plus mince. L?? encore, cela est d?? ?? l'action de la tension superficielle du mercure solide. La masse liquide se aplatit parce qui apporte le plus de mercure pour un niveau aussi bas que possible. Mais la tension de surface, en m??me temps, agit pour r??duire la surface totale. Le r??sultat est le compromis d'une flaque d'une ??paisseur presque fixe.

La m??me d??monstration de tension de surface peut ??tre effectu?? avec de l'eau, mais seulement sur une surface en une substance que l'eau ne respecte pas. La cire est une telle substance. L'eau vers??e sur une surface lisse, plane, horizontale cire, dire une feuille cir?? du verre, se comporte de mani??re similaire au mercure vers?? sur verre.

L'??paisseur d'une flaque de liquide sur une surface dont l'angle de contact est de 180 ?? est donn??e par:

$h \ = \ 2 \ sqrt {\ frac {\ gamma} {g \ rho}}$

o??

$\ Scriptstyle h$ est la profondeur de la flaque en centim??tres ou m??tres.

$\ Scriptstyle \ gamma$ est la tension superficielle du liquide en dynes par centim??tre ou newtons par m??tre.

$\ Scriptstyle g$ est l'acc??l??ration due ?? la gravit?? et est ??gale ?? 980 cm / s ² ou 9,8 m / s ²

$\ Scriptstyle \ rho$ est la masse volumique du liquide en grammes par centim??tre cube ou en kilogrammes par m??tre cube

Illustration de l'angle de contact comment inf??rieure conduit ?? la r??duction de la profondeur flaque d'eau

En r??alit??, les ??paisseurs des flaques d'eau seront un peu moins que ce qui est pr??vu par la formule ci-dessus parce que tr??s peu de surfaces ont un angle de 180 ?? avec un liquide de contact. Lorsque l'angle de contact est inf??rieur ?? 180 ??, l'??paisseur est donn??e par:

$h \ = \ \ sqrt {\ frac {2 \ gamma_ \ mathrm {la} \ left (1 - \ cos \ theta \ right)} {g \ rho}}$

Pour le mercure sur le verre, 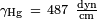$\ Scriptstyle \ gamma_ \ mathrm {Hg} \ = \ 487 \ \ mathrm {\ frac {} {dyn cm}}$ , $\ Scriptstyle \ rho_ \ mathrm {Hg} \ = \ 13.5 \ \ mathrm {\ frac {g} {cm ^ 3}}$ Et $\ Scriptstyle \ theta = 140 ^ \ circ$ , Ce qui donne $\ Scriptstyle h_ \ mathrm {Hg} \ = \ 0,36 \ \ mathrm {} cm$ . Pour l'eau de paraffine ?? 25 ?? 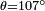C, $\ Scriptstyle \ gamma_ \ mathrm {H_2O} \ = \ 72 \ \ mathrm {\ frac {} {dyn cm}}$ , $\ Scriptstyle \ rho_ \ mathrm {H_2O} \ = 1,0 \ \ mathrm {\ frac {g} {cm ^ 3}}$ Et $\ Scriptstyle \ theta = 107 ^ \ circ$ ce qui donne $\ Scriptstyle h_ \ mathrm {H_2O} \ = \ 0,44 \ \ mathrm {} cm$ .

La formule pr??voit ??galement que lorsque l'angle de contact est de 0 ??, le liquide se ??tale en une couche de micro-mince sur la surface. Une telle surface est dite totalement mouillable par le liquide.

La rupture de flux en gouttes

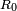??tape interm??diaire d'un jet rupture en gouttes. Des rayons de courbure dans la direction axiale sont pr??sent??es. L'??quation pour le rayon du flux est $\ Scriptstyle R \ gauche (z \ right) = R_0 + A_k \ cos \ left (kz \ right)$ O?? $\ Scriptstyle R_0$ est le rayon du jet non perturb??, 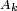$\ Scriptstyle A_k$ est l'amplitude de la perturbation, $\ Scriptstyle z$ est la distance le long de l'axe du courant, et $\ Scriptstyle k$ est le nombre d'onde

Dans la vie de tous les jours nous observons que un courant d'eau sortant d'un robinet briser en gouttelettes, ne importe comment en douceur le flux est ??mis par le robinet. Cela est d?? ?? un ph??nom??ne appel?? le Plateau-instabilit?? de Rayleigh, ce qui est tout ?? fait ?? la suite des effets de la tension superficielle.

L'explication de cette instabilit?? commence avec l'existence de petites perturbations dans le flux. Ce sont toujours pr??sents, ne importe comment lisser le flux est. Si les perturbations sont r??solus en composantes sinuso??dales, nous constatons que certains composants se d??veloppent avec le temps tandis que d'autres se d??sint??grent avec le temps. Parmi ceux qui poussent avec le temps, certains poussent ?? des taux plus rapides que d'autres. Que ce soit un composant d??cro??t ou cro??t, et la vitesse ?? laquelle elle pousse est enti??rement fonction de son nombre d'onde (une mesure de combien de pics et de creux par centim??tre) et le rayon du flux cylindrique d'origine. Le sch??ma de droite montre une exag??ration d'un seul composant.

En supposant que toutes les composantes possibles existent initialement dans amplitudes approximativement ??gales (mais minuscules), la taille des gouttes finales peut ??tre pr??dite par la d??termination de nombre d'onde o?? le composant se d??veloppe le plus rapidement. Au fil du temps, ce est la composante dont la croissance est maximale qui viendra ?? dominer et finira par ??tre celui qui pince le flux en gouttes.

Bien qu'une compr??hension approfondie de la fa??on dont cela se produit n??cessite une d??veloppement math??matique (voir les r??f??rences), le sch??ma peut fournir une compr??hension conceptuelle. Observez les deux bandes indiqu??es ceinturant le flux - un ?? un pic et l'autre ?? un creux de la vague. A l'auge, le rayon du courant est plus faible, donc en fonction de la ??quation de Young-Laplace (voir plus haut) la pression due ?? la tension de surface est augment??e. De m??me au sommet du rayon du courant est plus grande et, par le m??me raisonnement, la pression due ?? la tension superficielle est r??duite. Si ce ??tait le seul effet, nous nous attendons ?? ce que la pression plus ??lev??e dans la cuve serait presser liquide dans la r??gion de basse pression dans le pic. De cette fa??on, nous voyons comment la vague pousse dans amplitude dans le temps.

Mais le ??quation de Young-Laplace est influenc??e par deux composants distincts de rayon. Dans ce cas, on est le rayon, d??j?? discut??, du flux lui-m??me. L'autre est le rayon de courbure de l'onde elle-m??me. Les arcs encastr??s dans le diagramme montrent ceux-ci ?? un pic et ?? un creux. Notez que le rayon de courbure du creux est, en fait, n??gatif, ce qui signifie que, selon Young-Laplace, il diminue en fait la pression dans la cuve. De m??me, le rayon de courbure au sommet est positive et augmente la pression dans cette r??gion. L'effet de ces composants se trouve face aux effets du rayon du flux lui-m??me.

Les deux effets, en g??n??ral, ne se annulent pas exactement. L'un d'eux aura une plus grande ampleur que l'autre, selon le nombre d'onde et le rayon initial du flux. Lorsque le nombre d'onde est telle que le rayon de courbure de l'onde domine celle du rayon du flux, de tels composants ne se d??sint??grer au cours du temps. Lorsque l'effet du rayon du courant domine celle de la courbure de l'onde, ces composants se d??veloppent de fa??on exponentielle avec le temps.

Lorsque tout le calcul est effectu??, on constate que les composants instables (ce est-composants qui se d??veloppent dans le temps) sont celles o?? le produit du nombre d'onde avec le rayon initial est inf??rieur ?? l'unit?? ( $\ Scriptstyle kR_0 \ <\ 1$ ). La composante qui pousse le plus rapide est celui dont le nombre d'onde satisfait l'??quation:

$kR_0 \ \ simeq \ 0,697$

Thermodynamique

Comme indiqu?? plus haut, le travail m??canique n??cessaire pour augmenter une surface est $\ Scriptstyle dW \ = \ \ gamma dA$ . Par cons??quent, ?? temp??rature et pression constante, la tension de surface est ??gale ?? ??nergie libre de Gibbs par unit?? de surface:

$\ Gamma = \ left (\ frac {\ G partielle} {\ Un partielle} \ right) _ {T, P, n}$

o?? $\ Scriptstyle G$ Gibbs est l'??nergie libre et $\ Scriptstyle A$ est la zone.

Thermodynamique exige que tous les changements spontan??s d'Etat sont accompagn??s par une diminution de l'??nergie libre de Gibbs.

De cela, il est facile de comprendre pourquoi la diminution de la surface d'une masse de liquide est toujours spontan?? ( $\ Scriptstyle \ Delta G \ <\ 0$ ), ?? condition qu'elle ne est pas coupl??e ?? d'autres modifications de l'??nergie. Il se ensuit que, pour augmenter la surface, une certaine quantit?? d'??nergie doit ??tre ajout??.

??nergie libre de Gibbs est d??finie par l'??quation, 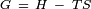$\ Scriptstyle G \ = \ H \ - \ TS$ O?? $\ Scriptstyle H$ est l'enthalpie et $\ Scriptstyle S$ est l'entropie . Sur la base de ceci et du fait que la tension de surface est libre de Gibbs ??nergie par unit?? de surface, il est possible d'obtenir l'expression suivante pour l'entropie par unit?? de surface:

$\ Left (\ frac {\ partial \ gamma} {\ T partielle} \ right) _ {A, P} = - S ^ {A}$

Kelvin de l'??quation pour les surfaces se pose en r??arrangeant les ??quations pr??c??dentes. Elle indique que l'enthalpie de surface ou de l'??nergie de surface (diff??rente de l'??nergie libre de surface) d??pend ?? la fois sur la tension superficielle et de son d??riv?? avec la temp??rature ?? pression constante par la relation.

$H ^ A \ = \ \ gamma - T \ left (\ frac {\ partial \ gamma} {\ T partielle} \ right) _P$

Influence de la temp??rature

Temp??rature d??pendance de la tension de surface du benz??ne

La tension de surface d??pend de la temp??rature. Pour cette raison, quand une valeur est donn??e ?? la tension superficielle d'une interface, la temp??rature doit ??tre explicitement indiqu??e. La tendance g??n??rale est que la tension superficielle diminue avec l'augmentation de la temp??rature, atteignant une valeur de 0 ?? la temp??rature critique. Pour plus de d??tails, voir E??tv??s r??gle. Il existe seulement ??quations empiriques pour rapporter la tension de surface et de la temp??rature:

E??tv??s:

$\ Gamma V ^ {2/3} = k (T_C-T) \, \!$

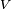$\ Scriptstyle V$ est le volume molaire de la substance
$\ Scriptstyle T_C$ est le temp??rature critique
$\ Scriptstyle k$ est une constante pour chaque substance.

Par exemple pour l'eau k = 1,03 erg / ?? C (103 nJ / K ), V = 18 ml / mole et T _C = 374 ?? C.

Une variante de E??tv??s est d??crit par Ramay et Shields:

$\ Gamma V ^ {2/3} = k \ gauche (T_C - T - 6 \ right)$

o?? le d??calage de temp??rature de 6 kelvins fournit la formule avec un meilleur ajustement ?? la r??alit?? ?? des temp??ratures inf??rieures.

Guggenheim-Katayama:

$\ Gamma = \ gamma ^ o \ left (1- \ frac {T} {} T_C \ right) ^ n$

$\ Scriptstyle \ gamma ^ o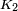$ est une constante pour chaque liquide et n est un facteur empirique, dont la valeur est 9.11 pour les liquides organiques. Cette ??quation a ??galement ??t?? propos?? par van der Waals, qui en outre propos?? que $\ Scriptstyle \ gamma ^ 0$ pourrait ??tre donn??e par l'expression, $\ Scriptstyle K_2 T ^ {\ frac {1} {3}} _ c P ^ {\ frac {2} {3}} _ c$ O?? $\ Scriptstyle K_2$ est une constante universelle pour tous les liquides, et $\ Scriptstyle P_c$ est le pression critique du liquide (bien que des exp??riences ult??rieures trouv?? 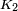$\ Scriptstyle K_2$ faire varier dans une certaine mesure d'un liquide ?? un autre).

Les deux Guggenheim-Katayama et E??tv??s prennent en compte le fait que la tension de surface atteint 0 ?? la temp??rature critique, alors que Ramay et Shields ne correspond pas ?? la r??alit?? ?? ce crit??re.

Influence de la concentration de solut??

Solut??s peuvent avoir diff??rents effets sur la tension de surface en fonction de leur structure:

Pas d'effet, par exemple le sucre
Augmentation de la tension superficielle, des sels inorganiques
Diminuer la tension de surface progressivement, alcools
Diminuer la tension de surface et, une fois minimum est atteint, pas plus d'effet: tensioactifs

Ce qui complique l'effet est un soluté qui peut exister en une concentration différente à la surface d'un solvant par rapport à son encombrement. Cette différence varie d'un soluté / combinaison de solvants à l'autre.

Gibbs isotherme stipule que: $\Gamma\ =\ - \frac{1}{RT} \left( \frac{\partial \gamma}{\partial \ln C} \right)_{T,P}$

$\scriptstyle \Gamma$ il est connu que la concentration de surface, il représente l'excès de soluté par unité de surface de la surface au-dessus de ce qui serait présente si la concentration apparente a prévalu tout le chemin vers la surface. Il a des unités de mol / m ²

$\scriptstyle C$ est la concentration de la substance dans la solution en vrac.

$\scriptstyle R$ est le constante des gaz et $\scriptstyle T$ latempérature

Certaines hypothèses sont prises dans sa déduction, donc Gibbs isotherme ne peut être appliquée à des solutions idéales (très diluées) à deux composantes.

Influence de la taille des particules sur la pression de vapeur

Le Formule de clapeyron conduit à une autre équation également attribué à Kelvin. Cela explique pourquoi, en raison de la tension superficielle, la pression de vapeur pour petites gouttelettes de liquide en suspension est supérieure à la pression de vapeur de la même norme de liquide lorsque l'interface est plate. Cela revient à dire que lorsqu'un liquide se forme de petites gouttelettes, la concentration d'équilibre de la vapeur dans son environnement est plus grande. Ceci vient du fait que la pression à l'intérieur de la gouttelette est plus grande qu'à l'extérieur.

$P_v^{fog}=P_v^o e^{\frac{V 2\gamma}{RT r_k}}$

Mol??cules ?? la surface d'une petite goutte (?? gauche) ont, en moyenne, moins de voisins que ceux sur une surface plane (?? droite). Par cons??quent, ils sont li??s plus faiblement ?? la gouttelette de mol??cules sont-surface plane.

$\ Scriptstyle P_v ^ o$ est la pression de vapeur standard pour ce liquide ?? cette temp??rature et de pression.
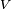$\ Scriptstyle V$ est le volume molaire.
$\ Scriptstyle R$ est le constante des gaz

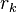$r_k$ est le rayon Kelvin, le rayon des gouttelettes.

L'effet explique sursaturation de vapeurs. En l'absence de sites de nucl??ation, de minuscules gouttelettes doivent former avant qu'ils peuvent ??voluer vers de plus grosses gouttelettes. Cela n??cessite de nombreuses fois par la pression de vapeur la pression de vapeur ?? la point de transition de phase.

Cette ??quation est ??galement utilis?? dans le catalyseur ?? ??valuer la chimie m??soporosit?? pour les solides.

L'effet peut ??tre consid??r?? en termes de nombre moyen de voisins mol??culaires de mol??cules de surface (voir sch??ma).

Le tableau montre quelques valeurs calcul??es de cet effet pour l'eau ?? diff??rentes tailles de gouttes:

P / P ₀ pour des gouttes d'eau ?? des rayons diff??rents STP
Rayon de gouttelettes (nm)	1000	100	10	1
P / P ₀	1,001	1,011	1,114	2,95

L'effet devient clair pour de très petites tailles de gouttes, comme une goutte de 1 rayon nm a environ 100 molécules à l'intérieur, ce qui est une quantité suffisamment petite pour nécessiter unemécanique quantiqueanalyse.

Tableau de données

Les données sont tiréesdu Manuel de Lange de Chimie, 10e éd.pp 1661-1665

La tension de surface de divers liquides dansdyn / cm contre l'air Mélange% 's sont en poids
Liquide	Température ° C	La tension de surface,??
Acide ac??tique	20	27,6
L'acide acétique (40,1%) + eau	30	40,68
L'acide acétique (10,0%) + eau	30	54.56
Ac??tone	20	23,7
De l'??ther di??thylique	20	17,0
??thanol	20	22.27
De l'éthanol (40%) + eau	25	29.63
De l'éthanol (11,1%) + eau	25	46,03
Glyc??rol	20	63
n-hexane	20	18,4
L'acide chlorhydrique17,7M de solution aqueuse	20	65,95
Isopropanol	20	21,7
Mercure	15	487
M??thanol	20	22,6
noctane	20	21,8
Chlorure de sodium 6,0 Solution aqueuse M	20	82,55
Saccharose(55%) + eau	20	76.45
Eau	0	75.64
Eau	25	71,97
Eau	50	67.91
Eau	100	58.85

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Surface_tension&oldid=199848525"