
Signifier
Renseignements g??n??raux
Ce contenu de Wikipedia a ??t?? s??lectionn?? par SOS Enfants d'aptitude dans les ??coles ?? travers le monde. Cliquez ici pour en savoir plus sur le parrainage d'enfants.
Dans les statistiques , la moyenne a deux significations connexes:
- la moyenne arithm??tique (et se distingue de la moyenne g??om??trique ou moyenne harmonique).
- la valeur attendue d'une variable al??atoire , qui est aussi appel?? la moyenne de population.
On dit parfois que la ??moyenne?? signifie moyenne. Ce est incorrect si "moyenne" est pris dans le sens sp??cifique de "moyenne arithm??tique" comme il existe diff??rents types de moyennes: la moyenne, la m??diane et le mode . Par exemple, les prix moyens des maisons utilisent presque toujours la valeur m??diane de la moyenne.
Pour une valeur r??elle variable al??atoire X, la moyenne est la esp??rance de X. On notera que chaque pas la distribution de probabilit?? a une moyenne d??finie (ou variance ); voir le Distribution de Cauchy pour un exemple.
Pour un ensemble de donn??es, la moyenne est la somme des observations divis?? par le nombre d'observations. La moyenne est souvent cit?? avec l' ??cart-type : la moyenne d??crit l'emplacement central des donn??es, et l'??cart type d??crit la propagation.
Une autre mesure de la dispersion est l'??cart moyen, ??quivalent ?? la moyenne d??viation absolue de la moyenne. Il est moins sensible aux valeurs aberrantes, mais moins math??matiquement traitable.
Ainsi que des statistiques, des moyens sont souvent utilis??s en g??om??trie et l'analyse; un large ??ventail de moyens ont ??t?? d??velopp??s pour ces fins, qui ne sont pas beaucoup utilis??s dans les statistiques. Ils sont ??num??r??s ci-dessous.
Des exemples de moyens
Moyenne arithm??tique
La moyenne arithm??tique est la moyenne "standard", souvent simplement appel??e la ??moyenne??.
La moyenne peut souvent ??tre confondue avec la m??diane ou le mode . La moyenne est la moyenne arithm??tique d'un ensemble de valeurs, ou la distribution; cependant, pour distributions asym??triques, la moyenne ne est pas n??cessairement la m??me que la valeur moyenne (m??diane), ou (mode) le plus probable. Par exemple, le revenu moyen est biais?? vers le haut par un petit nombre de personnes avec de tr??s gros revenus, de sorte que la majorit?? ont un revenu inf??rieur ?? la moyenne. En revanche, le revenu m??dian est le niveau auquel la moiti?? de la population est en dessous et la moiti?? est au-dessus. Le revenu de mode est le revenu le plus probable, et favorise le plus grand nombre de personnes ?? faible revenu. La m??diane ou le mode sont souvent des mesures plus intuitives de ces donn??es.
Cela dit, de nombreuses distributions asym??triques sont mieux d??crites par leur moyenne - comme les exponentielles et Poisson distributions.
Par exemple, la moyenne arithm??tique des 34, 27, 45, 55, 22, 34 (six valeurs) est (34 + 27 + 45 + 55 + 22 + 34) / 6 = 217/6 ≈ 36,167.
Moyenne g??om??trique
Le moyenne g??om??trique est une moyenne qui est utile pour les ensembles de nombres qui sont interpr??t??es en fonction de leur produit et non pas leur somme (comme ce est le cas avec la moyenne arithm??tique). Par exemple, les taux de croissance.
Par exemple, la moyenne g??om??trique de 34, 27, 45, 55, 22, 34 (six valeurs) est (34 ?? 27 ?? 45 ?? 55 ?? 22 ?? 34) 6.1 6.1 = 1699493400 = 34,545.
Moyenne harmonique
Le moyenne harmonique est une moyenne qui est utile pour des ensembles de nombres qui sont d??finis par rapport ?? certaines unit??, par exemple vitesse (distance par unit?? de temps).
Par exemple, la moyenne harmonique des nombres 34, 27, 45, 55, 22, et 34 est
Moyen g??n??ralis??
Puissance moyenne
Le moyenne g??n??ralis??e, aussi connu comme la puissance moyenne ou le titulaire dire, est une abstraction de la quadratique, l'arithm??tique, g??om??trique et des moyens harmoniques. Elle est d??finie par
En choisissant la valeur appropri??e pour le param??tre m nous obtenons
Click on the following link to visit or download this HTML page
 | maximum |
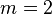 | moyenne quadratique, |
 | moyenne arithm??tique , |
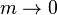 | moyenne g??om??trique, |
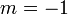 | harmonique signifie, |
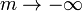 | minimum. |
f-moyen
Ceci peut ??tre g??n??ralis?? en outre que le f-g??n??ralis??e moyen
et encore un choix appropri?? d'un inversible 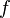 donnera
donnera
 | harmonique signifie, |
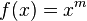 | moyen d'alimentation, |
 | moyenne g??om??trique. |
Moyenne pond??r??e
Le moyenne arithm??tique pond??r??e est utilis??e, si l'on veut combiner des valeurs moyennes ?? partir d'??chantillons de la m??me population avec diff??rentes tailles de l'??chantillon:
Les poids  repr??senter les limites de l'??chantillon partiel. Dans d'autres applications, ils repr??sentent une mesure de la fiabilit?? de l'influence sur la moyenne de valeurs respectives.
repr??senter les limites de l'??chantillon partiel. Dans d'autres applications, ils repr??sentent une mesure de la fiabilit?? de l'influence sur la moyenne de valeurs respectives.
Moyenne tronqu??e
Parfois, un ensemble de nombres (la donn??es) peut ??tre contamin??e par les valeurs aberrantes inexactes, ce est ?? dire des valeurs qui sont beaucoup trop bas ou trop ??lev??. Dans ce cas, on peut utiliser un moyenne tronqu??e. Il implique la suppression des parties des donn??es fournies en haut ou l'extr??mit?? inf??rieure, g??n??ralement un montant ??gal ?? chaque extr??mit??, puis en prenant la moyenne arithm??tique des donn??es restantes. Le nombre de valeurs retir??es est indiqu?? en pourcentage du nombre total de valeurs.
Interquartile signifie
Le interquartile signifie, ce est un exemple concret d'une moyenne tronqu??e. Ce est tout simplement la moyenne arithm??tique apr??s avoir retir?? le plus bas et le plus haut trimestre de valeurs.
en supposant que les valeurs ont ??t?? command??s.
Moyen d'une fonction
Dans le calcul , et surtout calcul ?? variables multiples, la moyenne d'une fonction est vaguement d??finie comme la valeur moyenne de la fonction sur sa domaine. Dans une variable, le moyen d'une fonction f (x) sur l'intervalle (a, b) est d??fini par
(Voir aussi valeur moyenne th??or??me.) Dans plusieurs variables, la moyenne sur une relativement compact domaine U dans un espace euclidien est d??finie par
Ceci g??n??ralise la moyenne arithm??tique. D'autre part, il est ??galement possible de g??n??raliser la moyenne g??om??trique de fonctions en d??finissant la moyenne g??om??trique de f pour ??tre
Plus g??n??ralement, th??orie de la mesure et de la th??orie des probabilit??s soit sorte de signifier joue un r??le important. Dans ce contexte, L'in??galit?? de Jensen place estimations pointus sur la relation entre ces deux notions diff??rentes de la moyenne d'une fonction.
Moyenne des angles
La plupart des moyens habituels ??chouent sur les quantit??s circulaires, comme les angles , daytimes, parties fractionnaires des nombres r??els . Pour les quantit??s que vous avez besoin d'un moyenne des quantit??s circulaires.
D'autres moyens
- Arithm??tique-moyenne g??om??trique
- Arithm??tique moyenne harmonique
- Lemme de Ces??ro
- Moyenne Chisini
- Moyenne Contraharmonic
- Moyenne sym??triques ??l??mentaires
- Moyenne g??om??trique harmonique
- Heinz signifie
- Moyenne Heronian
- Identric signifierait
- Moyenne des moindres carr??s
- Lehmer signifie
- Moyenne logarithmique
- M??diane
- Moyenne quadratique
- Stolarsky signifie
- Moyenne temporelle
- Moyenne g??om??trique pond??r??e
- Moyenne harmonique pond??r??e
- L'entropie de R??nyi (un g??n??ralis??e f-moyen)
Propri??t??s
La m??thode la plus g??n??rale pour d??finir une moyenne ou moyenne, y, prend toute fonction d'une liste g (x_1, x_2, ..., xn), qui est sym??trique par permutation des membres de la liste, et l'assimile ?? la m??me fonction de la valeur de la moyenne remplacement de chaque membre de la liste: g (x 1, x_2, ..., xn) = g (y, y, ..., y). Tous les moyens part certaines propri??t??s et d'autres propri??t??s sont partag??es par les moyens les plus courants. Certaines de ces propri??t??s sont collect??s ici.
Moyenne pond??r??e
Une moyenne pond??r??e  est une fonction qui associe uplets de nombres positifs ?? un nombre positif (
est une fonction qui associe uplets de nombres positifs ?? un nombre positif ( 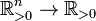 ).
).
- " Point fixe ":

- Homog??n??it??:
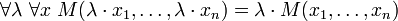
- (En utilisant notation vectorielle:
 )
)
- (En utilisant notation vectorielle:
- Monotonie:

Cela suit
- Born??:
![\ Forall x \ M x \ in [\ x min, \ max x]](../../images/135/13510.png)
- Continuit??:

- Croquis d'une preuve: Parce que
 et
et 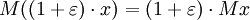 cela suit
cela suit  .
.
- Il existe des moyens qui ne sont pas d??rivables . Par exemple, le nombre maximal d'un tuple est consid??r??e comme un moyen (comme un cas extr??me de la puissance moyenne, ou comme un cas particulier d'une m??diane ), mais ne est pas diff??rentiable.
- Tous les moyens ??num??r??s ci-dessus, ?? l'exception de la majeure partie de la F-moyen g??n??ralis??, satisfont les propri??t??s pr??sent??es.
- Si
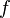 est bijective, le f-moyenne g??n??ralis??e satisfait la propri??t?? de point fixe.
est bijective, le f-moyenne g??n??ralis??e satisfait la propri??t?? de point fixe. - Si
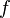 est strictement monotone, le f-moyenne g??n??ralis??e satisfaire ??galement la propri??t?? de monotonie.
est strictement monotone, le f-moyenne g??n??ralis??e satisfaire ??galement la propri??t?? de monotonie. - En g??n??ral, un f-moyenne g??n??ralis??e ratera homog??n??it??.
- Si
Les propri??t??s ci-dessus impliquent des techniques pour construire des moyens plus complexes:
Si 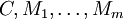 des moyens pond??r??s,
des moyens pond??r??s, 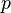 est un facteur positif nombre r??el , alors
est un facteur positif nombre r??el , alors 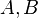 avec
avec
sont ??galement une moyenne pond??r??e.
Moyenne non pond??r??e
Intuitivement parl??, moyenne non pond??r??e est une moyenne pond??r??e avec des poids ??gaux. Depuis notre d??finition de la moyenne pond??r??e ci-dessus ne expose pas des poids particuli??res, des poids ??gaux doivent ??tre maintenus par un autre chemin. Un point de vue diff??rent sur la pond??ration est homog??ne, que les entr??es peuvent ??tre ??chang??s sans alt??rer le r??sultat.
Ainsi nous d??finissons  ??tant une moyenne non pond??r??e se il se agit d'une moyenne pond??r??e, et pour chaque permutation
??tant une moyenne non pond??r??e se il se agit d'une moyenne pond??r??e, et pour chaque permutation 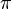 des entr??es, le r??sultat est le m??me. Laisser
des entr??es, le r??sultat est le m??me. Laisser 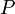 comme l'ensemble des permutations de
comme l'ensemble des permutations de  -uplets.
-uplets.
- Sym??trie:

De mani??re analogue aux moyens pond??r??s, si 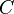 est une moyenne pond??r??e et
est une moyenne pond??r??e et  sont des moyens non pond??r??s,
sont des moyens non pond??r??s, 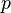 est un facteur positif nombre r??el , alors
est un facteur positif nombre r??el , alors 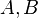 avec
avec
sont ??galement des moyens non pond??r??s.
Convertir moyenne non pond??r??e ?? moyenne pond??r??e
Une moyenne non pond??r??e peut ??tre transform?? en une moyenne pond??r??e par des ??l??ments r??p??ter. Cette connexion peut ??galement ??tre utilis?? pour indiquer qu'une moyenne est la version pond??r??e d'une moyenne non pond??r??e. Disons que vous avez la moyenne non pond??r??e  et le poids des chiffres par des nombres naturels
et le poids des chiffres par des nombres naturels  . (Si les chiffres sont rationnelle , puis les multiplier avec le d??nominateur commun moins). Puis la moyenne pond??r??e correspondante
. (Si les chiffres sont rationnelle , puis les multiplier avec le d??nominateur commun moins). Puis la moyenne pond??r??e correspondante  est obtenu par
est obtenu par
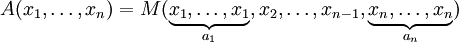 .
.
Moyens de tuples de diff??rentes tailles
Si un moyen  est d??fini pour plusieurs tuples de taille, alors on se attend ??galement que la moyenne d'un tuple est d??limit??e par le moyen de cloisons. Plus pr??cis??ment
est d??fini pour plusieurs tuples de taille, alors on se attend ??galement que la moyenne d'un tuple est d??limit??e par le moyen de cloisons. Plus pr??cis??ment
- Compte tenu d'un tuple arbitraire
 , Qui est partitionn?? en
, Qui est partitionn?? en  , Alors il d??tient
, Alors il d??tient  . (Voir Enveloppe convexe)
. (Voir Enveloppe convexe)
L'enseignement des math??matiques
Dans de nombreuses normes de l'Etat et programmes du gouvernement, les ??l??ves sont cens??s traditionnellement ?? apprendre ni le sens ni la formule de calcul de la moyenne par la quatri??me ann??e. Cependant, dans de nombreux programmes de math??matiques bas??e sur les standards, les ??tudiants sont encourag??s ?? inventer leurs propres m??thodes, et ne peuvent ??tre enseign??es la m??thode traditionnelle. textes de r??forme de base tels que TERC en fait d??courager l'enseignement de la traditionnelle "ajouter les num??ros et diviser par le nombre d'??l??ments" m??thode en faveur de passer plus de temps sur le concept de la m??diane , qui ne n??cessite pas la division. Cependant, la moyenne peut ??tre calcul??e avec une calculatrice ?? quatre fonctions simple, tandis que la m??diane n??cessite un ordinateur. Le m??me guide de l'enseignant consacre plusieurs pages sur la fa??on de trouver la m??diane d'un ensemble, qui est jug??e plus simple que de trouver la moyenne.


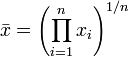

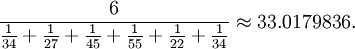
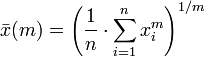
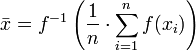

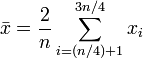

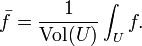
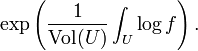
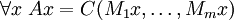
![\ Forall x \ B x = \ sqrt [p] {C (x_1 ^ p, \ dots, x_n ^ p)}](../../images/135/13518.png)
![\ Forall x \ B x = \ sqrt [p] {M_1 (x_1 ^ p, \ dots, x_n ^ p)}](../../images/135/13521.png)
