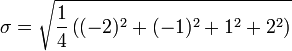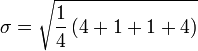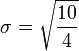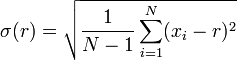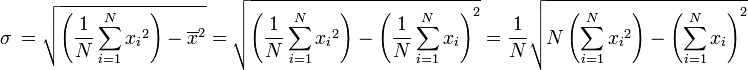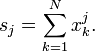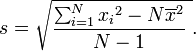L'??cart-type
Contexte des ??coles Wikip??dia
Arrangeant une s??lection Wikipedia pour les ??coles dans le monde en d??veloppement sans internet ??tait une initiative de SOS Enfants. Voir http://www.soschildren.org/sponsor-a-child pour conna??tre le parrainage d'enfants.
En probabilit?? et statistiques , l'??cart-type d'une distribution de probabilit?? , variable al??atoire , ou la population ou multi-ensemble de valeurs est une mesure de la propagation de ses valeurs. L'??cart-type est habituellement not??e par la lettre σ (minuscules Sigma). Il est d??fini comme la racine carr??e de la variance .
Pour comprendre l'??cart type, garder ?? l'esprit que la variance est la moyenne des carr??s des diff??rences entre les points de donn??es et la moyenne. La variance est sous forme de tableaux en unit??s carr??s. L'??cart-type, soit la racine carr??e de cette quantit??, mesure donc la propagation de donn??es sur la moyenne, mesur??e dans les m??mes unit??s que les donn??es.
De fa??on plus formelle, l'??cart-type est la moyenne quadratique (RMS) type des valeurs de leur moyenne arithm??tique .
Par exemple, dans la population {4, 8}, la moyenne est 6 et les ??carts par rapport aux moyennes sont {-2, 2}. Ces ??carts carr??s sont {4, 4} dont la moyenne (la variance) est 4. Par cons??quent, l'??cart type est ??gal ?? 2. Dans ce cas, 100% des valeurs dans la population sont ?? un ??cart-type de la moyenne.
L'??cart-type est la mesure la plus courante de dispersion statistique, la mesure de la fa??on dont les valeurs largement r??pandu dans un ensemble de donn??es sont. Si nombreux points de donn??es sont proches de la moyenne, alors l'??cart type est faible; si nombreux points de donn??es sont loin de la moyenne, alors l'??cart type est grande. Si toutes les valeurs de donn??es sont ??gales, l'??cart type est ??gal ?? z??ro.
Pour un population, l'??cart type peut ??tre estim?? par un ??cart-type (s) de modification d'un ??chantillon. Les formules sont donn??es ci-dessous.

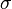 est une mesure de la dispersion des valeurs de la variable al??atoire loin de sa moyenne
est une mesure de la dispersion des valeurs de la variable al??atoire loin de sa moyenne 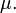
D??finition et calcul
Un exemple simple
Supposons que nous souhaitions pour trouver l'??cart type de l'ensemble des num??ros 4 et 8.
??tape 1: trouver la moyenne arithm??tique (ou moyenne) de 4 et 8,
??tape 2: trouver le type de chaque num??ro de la moyenne,
??tape 3: carr??s chacune des ??carts (amplification des ??carts plus importants et faire des valeurs n??gatives positif),
??tape 4: somme des carr??s obtenus (comme une premi??re ??tape ?? l'obtention d'une moyenne),
Etape 5: diviser la somme par le nombre de valeurs, qui ici est ??gal ?? 2 (soit une moyenne),
 = 4.
= 4.
??tape 6: prendre la racine carr??e positive du quotient (conversion d'unit??s au carr?? revenir ?? des unit??s r??guli??res),
Ainsi, l'??cart type est de 2.
L'??cart-type d'une variable al??atoire
L'??cart-type d'une variable al??atoire X est d??fini comme:
o?? E (X) est le valeur attendue de X, et Var (X) est la variance de x.
Toutes les variables al??atoires ne ont pas un ??cart-type, puisque ceux-ci valeurs attendues ne ont pas besoin existent. Par exemple, l'??cart type d'une variable al??atoire qui suit une Distribution de Cauchy est ind??fini parce que son E (X) ne est pas d??finie.
Si la variable al??atoire X prend les valeurs 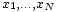 (Qui sont des nombres r??els ) avec une probabilit?? ??gale, puis son ??cart-type peut ??tre calcul?? comme suit. Tout d'abord, le moyen de X,
(Qui sont des nombres r??els ) avec une probabilit?? ??gale, puis son ??cart-type peut ??tre calcul?? comme suit. Tout d'abord, le moyen de X,  , Est d??fini comme un sommation:
, Est d??fini comme un sommation:
o?? N est le nombre d'??chantillons pr??lev??s. Ensuite, l'??cart-type se simplifie
En d'autres termes, l'??cart type d'une variable al??atoire uniforme discr??te X peut ??tre calcul?? comme suit:
- Pour chaque valeur
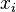 calculer la diff??rence
calculer la diff??rence 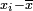 entre x i et la valeur moyenne
entre x i et la valeur moyenne  .
. - Calculer les carr??s de ces diff??rences.
- Trouver la moyenne des carr??s des ??carts. Cette quantit?? est la variance σ 2.
- Prendre la racine carr??e de la variance.
L'expression ci-dessus peut ??galement ??tre remplac?? par
L'??galit?? de ces deux expressions peut ??tre d??montr?? par un peu d'alg??bre:
L'??cart-type d'une variable al??atoire continue
Distributions continues donnent g??n??ralement une formule de calcul de l'??cart-type en fonction des param??tres de la distribution. En g??n??ral, l'??cart type d'une variable al??atoire continue X avec fonction de densit?? de probabilit?? p (x) est
O??
Exemple
Nous allons montrer comment calculer l'??cart-type d'une population. Notre exemple va utiliser les ??ges de quatre jeunes enfants: {5, 6, 8, 9}.
??tape 1. Calculer la moyenne arithm??tique ,  :
:
Nous avons N = 4 parce qu'il ya quatre points de donn??es:
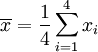 Suppl??ant N = 4
Suppl??ant N = 4
??tape 2. Calculer l'??cart type,  . (Depuis les quatre valeurs repr??sentent l'ensemble de la population, nous ne utilisons pas la formule de l'??cart type estim?? dans ce cas):
. (Depuis les quatre valeurs repr??sentent l'ensemble de la population, nous ne utilisons pas la formule de l'??cart type estim?? dans ce cas):
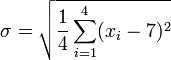 Rempla??ant
Rempla??ant  = 7 et N = 4
= 7 et N = 4
Donc, l'??cart type des ??ges des quatre enfants est la racine carr??e de 2,5, soit environ 1,58.
Se il en ??tait fix?? un ??chantillon tir?? d'une population plus grande des enfants, et la question ??tait ?? port??e de main une estimation de l'??cart type de la population, convention remplacerait le d??nominateur N (ou 4) ?? l'??tape 2 ici avec N -1 (ou 3 ).
Interpr??tation et application
Un grand ??cart-type indique que les points de donn??es sont loin de la moyenne et un petit ??cart type indique qu'ils sont regroup??s en ??troite collaboration autour de la moyenne.
Par exemple, chacun des trois ensembles de donn??es {0, 0, 14, 14}, {0, 6, 8, 14} et {6, 6, 8, 8} a une moyenne de 7. Les ??carts-types sont 7, 5 et 1, respectivement. Le troisi??me set a un ??cart type beaucoup plus petit que les deux autres parce que ses valeurs sont toutes proche de 7. Dans un sens large, l'??cart-type nous dit comment loin de la moyenne des points de donn??es ont tendance ?? ??tre. Il aura les m??mes unit??s que se rappelle les donn??es. Si, par exemple, l'ensemble de donn??es {0, 6, 8, 14} repr??sente les ??ges de quatre fr??res et s??urs dans les ann??es, l'??cart type est de 5 ans.
Comme autre exemple, l'ensemble de donn??es {1000, 1006, 1008, 1014} peut repr??senter les distances parcourues par quatre athl??tes, mesur??e en m??tres. Elle a une moyenne de 1007 m??tres, et un ??cart type de 5 m??tres.
L'??cart-type peut servir de mesure de l'incertitude. En sciences physiques, par exemple, l'??cart type rapport?? d'un groupe d'r??p??t??s mesures devrait donner le pr??cision de ces mesures. Au moment de d??cider si les mesures sont d'accord avec une pr??diction th??orique, l'??cart-type de ces mesures est d'une importance cruciale: si la moyenne des mesures est trop loin de la pr??diction (avec la distance mesur??e en ??carts-types), alors la th??orie test??e probablement doit ??tre r??vis??e. Ce est logique car ils sortent la gamme des valeurs qui pourraient raisonnablement se attendre ?? se produire si la pr??diction ??tait correcte et l'??cart type de quantifier de fa??on appropri??e. Voir intervalle de pr??diction.
Exemples de la vie r??elle
La valeur pratique de la compr??hension de l'??cart-type d'un ensemble de valeurs est ?? appr??cier le degr?? de variation il ya de la ??moyenne?? (signifie).
Temps
Comme un exemple simple, consid??rons les temp??ratures moyennes pour les villes. Alors que les deux villes peuvent avoir chacun une temp??rature moyenne de 60 ?? F, il est utile de comprendre que la gamme pour les villes pr??s de la c??te est plus faible que pour les villes int??rieures, qui pr??cise que, alors que la moyenne est similaire, la chance de la variation est sup??rieur ?? l'int??rieur des terres pr??s de la c??te.
Ainsi, une moyenne de 60 se produit pour une ville avec des sommets de 80 ?? F et les bas de 40 ?? F, et se produit ??galement une autre ville avec des hauts et des bas de 65 de 55. L'??cart-type nous permet de reconna??tre que la moyenne de la ville avec la plus grande variation, et donc un ??cart-type sup??rieur, ne offrira pas une pr??diction fiable de la temp??rature que la ville avec la plus petite variation et ??cart-type inf??rieur.
Sportif
Une autre fa??on de le voir est de consid??rer les ??quipes sportives. En tout ensemble de cat??gories, il y aura des ??quipes qui ??valuent tr??s ?? certaines choses et mal ?? d'autres. Il ya des chances, les ??quipes qui m??nent au classement ne sera pas montrer telle disparit??, mais seront assez bonne dans la plupart des cat??gories. Plus la d??viation standard de leurs notes dans chaque cat??gorie, plus ??quilibr??e et coh??rente qu'ils pourraient ??tre. Ainsi, une ??quipe qui est toujours mauvaise dans la plupart des cat??gories aura un faible ??cart type. Une ??quipe qui est toujours tr??s bon dans la plupart des cat??gories aura ??galement un ??cart type faible. Une ??quipe avec un ??cart-type ??lev?? pourrait ??tre le type d'??quipe qui marque beaucoup (forte infraction), mais conc??de aussi beaucoup (de faible d??fense), ou vice versa, qui pourraient avoir une mauvaise infraction, mais compense en ??tant difficile de marquer sur -teams avec un ??cart-type sup??rieur sera plus impr??visible.
Essayer de pr??dire quelles ??quipes, sur ne importe quel jour donn??, va gagner, peut comprendre en regardant les ??carts-types des diff??rents ??quipe "stats" votes, dans lequel les anomalies peuvent ??galer forces contre les faiblesses de tenter de comprendre quels facteurs peuvent l'emporter que des indicateurs solides des r??sultats ??ventuels de notation.
En course, un pilote est chronom??tr?? sur tours successifs. Un conducteur ayant un faible ??cart type des temps au tour est plus coh??rente que le conducteur avec un ??cart type sup??rieur. Cette information peut ??tre utilis??e pour aider ?? comprendre o?? les possibilit??s pourraient ??tre trouv??es pour r??duire les temps au tour.
Financement
En finance, l'??cart type est une repr??sentation du risque associ?? ?? un titre donn?? (des actions, obligations, immobilier, etc.), ou le risque d'un portefeuille de valeurs mobili??res. Le risque est un facteur important dans la d??termination de la fa??on de g??rer efficacement un portefeuille de placements, car il d??termine la variation des rendements sur l'actif et / ou portefeuille et donne aux investisseurs une base math??matique pour les d??cisions d'investissement. Le concept global de risque, ce est que comme il augmente, le rendement attendu de l'actif va augmenter en raison de la prime de risque gagn?? - en d'autres termes, les investisseurs devraient se attendre ?? un rendement plus ??lev?? sur un investissement lorsque ledit investissement comporte un niveau de risque plus ??lev?? .
Par exemple, vous avez le choix entre deux stocks: Stock A renvoie historiquement 5% avec un ??cart type de 10%, tandis que l'action B retourne 6% et porte un ??cart-type de 20%. Sur la base de risque et de rendement, un investisseur peut d??cider que Stock A est le meilleur choix, parce suppl??mentaire point de pourcentage de Stock B de rendement g??n??r?? (de 20% suppl??mentaires en termes de dollars) ne vaut pas le double du degr?? de risque associ?? ?? Stock A . Stock B est susceptible de tomber ?? court de l'investissement initial plus souvent Stock A dans les m??mes circonstances, et sera de retour seulement un point de pourcentage de plus en moyenne. Dans cet exemple, Stock A a le potentiel pour gagner 10% de plus que le rendement attendu, mais est ??galement susceptible de gagner 10% de moins que le rendement attendu.
Calcul du rendement moyen (ou moyenne arithm??tique) d'un titre sur un nombre donn?? de p??riodes va g??n??rer un rendement sur l'actif. Pour chaque p??riode, en soustrayant le rendement attendu des r??sultats de rendement r??el de la variance. Carr?? de la variance dans chaque p??riode pour trouver l'effet du r??sultat sur le risque global de l'actif. Plus la variance dans une p??riode, le plus grand risque ?? la s??curit?? porte. Prenant la moyenne des ??carts au carr?? r??sulte dans la mesure de l'ensemble des unit??s de risque associ??s ?? l'actif. Trouver la racine carr??e de cette variance se traduira par l'??cart-type de l'outil d'investissement en question. Utilisez cette mesure, combin??e avec le rendement moyen sur la s??curit??, comme base pour comparer les valeurs mobili??res.
Interpr??tation g??om??trique
Pour gagner quelques id??es g??om??triques, nous allons commencer avec une population de trois valeurs, x 1, x 2, x 3. Ceci d??finit un point P = (x 1, x 2, x 3) dans R 3. Consid??rez la ligne L = {(r, r, r): r dans R}. Ce est la "diagonale principale" passant par l'origine. Si nos trois valeurs donn??es ??taient tous ??gaux, alors l'??cart-type serait z??ro et P serait mentir sur L. Il ne est donc pas d??raisonnable de supposer que l'??cart type est li??e ?? la distance de P ?? L. Et ce est effectivement le cas. D??m??nagement orthogonale de P ?? la ligne L, on frappe le point:
dont les coordonn??es sont la moyenne des valeurs Nous avons commenc?? avec. Un peu d'alg??bre montre que la distance entre P et R (qui est la m??me que la distance entre P et la ligne L) est donn??e par σ√ 3. Une formule analogue (avec 3 remplac?? par N) est ??galement valable pour une population de N valeurs; il faut alors travailler dans R N.
R??gles pour les donn??es normalement distribu??es
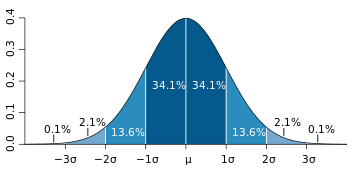
Dans la pratique, on suppose souvent que les donn??es proviennent d'un peu pr??s normalement distribu??e population. Ce est souvent justifi??e par le classique th??or??me central limite, qui dit que les sommes de plusieurs variables al??atoires ind??pendantes, identiquement distribu??es tendent vers la distribution normale comme une limite. Si cette hypoth??se est justifi??e, environ 68% des valeurs sont ?? 1 ??cart type de la moyenne, environ 95% des valeurs sont dans les deux ??carts-types et environ 99,7% se situent dans trois ??carts-types. Ceci est connu comme la R??gle 68-95-99.7, ou la r??gle empirique.
Le les intervalles de confiance sont les suivantes:
| σ | 68,26894921371% |
| 2σ | 95,44997361036% |
| 3σ | 99,73002039367% |
| 4σ | 99,99366575163% |
| 5σ | 99,99994266969% |
| 6σ | 99,99999980268% |
| 7σ | 99,99999999974% |
Pour les distributions normales, les deux points de la courbe qui sont un ??cart-type de la moyenne sont ??galement la les points d'inflexion.
L'in??galit?? de Tchebychev
L'in??galit?? de Chebyshev prouve que dans ne importe quel ensemble de donn??es, la quasi-totalit?? des valeurs sera plus proche de la valeur moyenne, o?? le sens de "pr??s de" est sp??cifi?? par l'??cart type. L'in??galit?? de Chebyshev implique que pour (presque) toutes les distributions al??atoires, et pas seulement celles normales, nous avons le plus faibles limites suivantes:
- Au moins 50% des valeurs sont ?? √2 ??carts types de la moyenne.
- Au moins 75% des valeurs sont dans les deux ??carts types de la moyenne.
- Au moins 89% des valeurs sont dans les 3 ??carts-types de la moyenne.
- Au moins 94% des valeurs sont dans les 4 ??carts types de la moyenne.
- Au moins 96% des valeurs sont ?? 5 ??carts-types de la moyenne.
- Au moins 97% des valeurs sont dans les six ??carts types de la moyenne.
- Au moins 98% des valeurs sont dans les 7 ??carts types de la moyenne.
Et en g??n??ral:
- Au moins (1 - 1 / k 2) ?? 100% des valeurs sont dans ??carts-types de la moyenne de k.
Relation entre l'??cart type et moyen
La moyenne et l'??cart-type d'un ensemble de donn??es sont g??n??ralement d??clar??s ensemble. Dans un certain sens, l'??cart-type est une mesure ??naturelle?? de dispersion statistique si le centre de donn??es est mesur?? autour de la moyenne. Ce est parce que l'??cart type de la moyenne est plus petite que de tout autre point. La d??claration pr??cise est la suivante: supposons x 1, ..., x n sont des nombres r??els et de d??finir la fonction:
Utilisation de calcul , ou simplement par compl??tant le carr??, il est possible de montrer que σ (r) a un minimum unique au moyen:
(Ceci peut ??galement ??tre fait avec l'alg??bre assez simple seul, puisque σ 2 (R) est assimil?? ?? un polyn??me du second degr??).
Le coefficient de variation d'un ??chantillon est le rapport de l'??cart type ?? la moyenne. C'est un nombre sans dimension qui peut ??tre utilis?? pour comparer la quantit?? de la variance entre les populations avec des moyens diff??rents.
M??thodes de calcul rapides
Un peu plus rapidement (de mani??re significative pour l'ex??cution de l'??cart type) moyen de calculer la norme de population d??viation est donn??e par la formule suivante (bien que des consid??rations doivent ??tre prises pour erreur d'arrondi, d??passement arithm??tique, et conditions Soupassement arithm??tique):
ou
o?? S 2 sont d??finis les sommes de puissance S 0, S 1, par
De m??me pour l'??cart type ??chantillon:
Ou de se ex??cuter sommes:


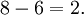
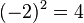
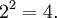




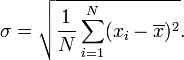

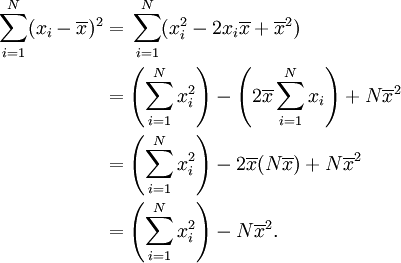
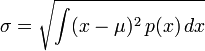
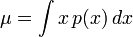
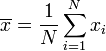

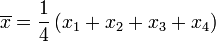



![\ Sigma = \ sqrt {\ frac {1} {4} \ left [(x_1 - 7) ^ 2 + (x_2 - 7) ^ 2 + (x_3 - 7) ^ 2 + (x_4 - 7) ^ 2 \ right ]}](../../images/135/13580.png)
![\ Sigma = \ sqrt {\ frac {1} {4} \ left [(5-7) ^ 2 + (6-7) ^ 2 + (8-7) ^ 2 + (9-7) ^ 2 \ right ]}](../../images/135/13581.png)