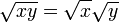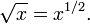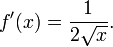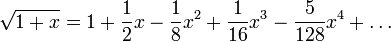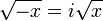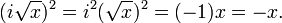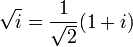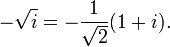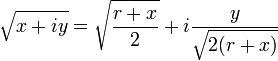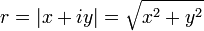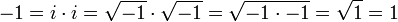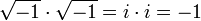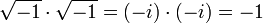Racine carr??e

Renseignements g??n??raux

Cette s??lection ??coles a ??t?? choisi par SOS Enfants pour les ??coles dans le monde en d??veloppement ne ont pas acc??s ?? Internet. Il est disponible en t??l??chargement intranet. Tous les enfants disponibles pour le parrainage de SOS Enfants des enfants sont pris en charge dans une maison de famille pr??s de la charit??. Lire la suite ...

En math??matiques , une racine carr??e (√) d'un nombre x est un nombre r tel que r ² = x, ou dans des mots, un nombre r dont carr?? (le r??sultat de la multiplication du nombre par lui-m??me) est x. Chaque non-n??gative nombre r??el x a une racine carr??e positive unique, appel??e la racine carr??e principale et not??e avec un symbole radical √ x. Par exemple, la principale racine carr??e de 9 est 3, not??e √ 9 = 3, parce 3 ² = 3 x 3 = 9.

Racines carr??es surgissent souvent lors de la r??solution des ??quations du second degr?? , ou ??quations de la forme ax ² + bx + c = 0, en raison de la variable x ??tant carr??.

Chaque nombre x positive a deux racines carr??es. L'un d'eux est √ x, qui est positif, et les autres -√ x, ce qui est n??gatif. Ensemble, ces deux racines sont not??es ?? √ x. Racines carr??es de nombres n??gatifs peuvent ??tre discut??es dans le cadre de nombres complexes . Racines carr??es d'objets autres que des chiffres peuvent ??galement ??tre d??finis.

Racines carr??es des nombres entiers qui ne sont pas carr??s parfaits sont toujours des nombres irrationnels : les num??ros ne est pas exprimable comme un rapport de deux nombres entiers. Par exemple, √ 2 ne peut pas ??tre ??crit exactement comme m / n, o?? n et m sont des nombres entiers. N??anmoins, ce est exactement la longueur de la diagonale d'un carr?? dont les c??t??s mesurent 1. Cela a ??t?? connu depuis l'Antiquit??, avec la d??couverte que √ 2 est irrationnelle attribu?? ?? Hipparque, un disciple de Pythagore . (Voir racine carr??e de 2 des preuves de l'irrationalit?? de ce num??ro.)

Propri??t??s

Le graphe de la fonction f (x) = √ x, constitu?? d'une moiti?? avec une parabole verticale directrice.

La principale fonction de la racine carr??e f (x) = x √ (habituellement appel??e la "fonction de la racine carr??e") est une fonction qui associe la ensemble de non-n??gative nombres r??els R ⁺ ∪ {0} sur lui-m??me, et, comme toutes les fonctions, renvoie toujours une valeur unique. La fonction de la racine carr??e mappe ??galement des nombres rationnels dans nombres alg??briques (un sur-ensemble des nombres rationnels); √ x est rationnel si et seulement si x est un nombre rationnel qui peut ??tre repr??sent?? comme un rapport de deux carr??s parfaits. Dans g??om??triques termes, la fonction de la racine carr??e mappe la zone d'un carr?? ?? sa longueur de c??t??.

Pour tous les nombres r??els x,

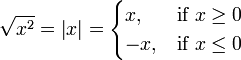$\ Sqrt {x ^ 2} = \ left | x \ right | = \ begin {} x cas, et \ mbox {if} x \ ge 0 \\ -x, & \ mbox {if} x \ le 0 \ end {} cas$ (Voir valeur absolue )

Pour tous les non-n??gatifs nombres r??els x et y,

$\ Sqrt {xy} = \ sqrt x \ sqrt y$

$\ Sqrt x = x ^ {1/2}.$

La fonction de la racine carr??e est continue pour tout x non-n??gatifs et diff??rentiable pour tout x positifs. Son d??riv?? est donn??e par

$f '(x) = \ frac {1} {2 \ sqrt x}.$

La s??rie de Taylor de √ 1 + x sur x = 0 converge pour | x | <1 et est donn??e par

$\ Sqrt {x} + 1 = 1 + \ frac {1} {2} x - \ frac {1} {8} x ^ 2 + \ frac {1} {16} x ^ 3 - \ frac {5} { 128} x ^ 4 + \ dots \!$

Calcul

Beaucoup de m??thodes de calcul des racines carr??es existent aujourd'hui, certains destin??s ?? ??tre fait ?? la main et certains destin?? ?? ??tre fait par la machine.

Beaucoup, mais pas tous les calculatrices de poche ont une cl?? de la racine carr??e. Ordinateur tableurs et autres logiciels sont aussi fr??quemment utilis?? pour calculer des racines carr??es. programmes de logiciels informatiques ?? mettre en ??uvre g??n??ralement bonnes routines pour calculer la fonction exponentielle et logarithme naturel ou logarithme , puis calculer la racine carr??e de x en utilisant l'identit??

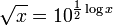
$\ Sqrt {x} = e ^ {\ frac {1} {2} \ ln x}$ ou $\ Sqrt {x} = 10 ^ {\ frac {1} {2} \ log x}$

La m??me identit?? est exploit??e lors du calcul des racines carr??es avec tables de logarithmes ou r??gles ?? calcul.

La m??thode la plus commune de calcul de la racine carr??e ?? la main est connu comme le " . M??thode babylonienne "Il se agit d'un algorithme simple, qui se traduit par un certain nombre de plus pr??s ?? la racine carr??e r??elle chaque fois qu'il est r??p??t?? Pour trouver r, la racine carr??e d'un nombre r??el x.:

Commencez avec une valeur r de d??part positif arbitraire (la plus proche de la racine carr??e de x, mieux ce est).
Remplacer r par la moyenne entre r et x / r. (Il suffit de prendre une valeur approximative de la moyenne, pas trop proche de la valeur pr??c??dente de r et x / r afin de garantir convergence).
R??p??tez l'??tape 2 jusqu'?? ce que r et x / r sont aussi proche que d??sir??.

Les plus connus complexit?? en temps de calcul d'une racine carr??e de n chiffres de pr??cision est la m??me que pour la multiplication de deux nombres ?? chiffres n.

Racines carr??es de nombres n??gatifs et complexes

Racine carr??e complexe

Deuxi??me feuilles de la racine carr??e complexe

Utilisation de la surface de Riemann de la racine carr??e, on peut voir comment les deux feuilles se imbriquent

Le carr?? d'un nombre positif ou n??gatif est positif, et le carr?? de 0 est 0. Par cons??quent, aucun num??ro n??gative pouvez avoir une vraie racine carr??e. Cependant, il est possible de travailler avec un plus grand ensemble de nombres, appel?? les nombres complexes , qui contient des solutions ?? la racine carr??e d'un nombre n??gatif. Ceci est r??alis?? par l'introduction d'un nouveau num??ro, not?? i (j parfois, en particulier dans le contexte de ??lectricit??) et appel??e unit?? imaginaire , qui est d??finie de telle sorte que i ² = -1. En utilisant cette notation, nous pouvons penser i comme la racine carr??e de -1, mais remarquerez que nous avons ??galement (- i) ² = i ² = -1 et ainsi de - i est aussi une racine carr??e de -1. De m??me que pour les nombres r??els, nous disons que la principale racine carr??e de -1 est i, ou plus g??n??ralement, si x est un nombre positif, alors la principale racine carr??e de - x est

$\ Sqrt {-x} = i \ sqrt x$

parce que

$(I \ sqrt x) ^ 2 = i ^ 2 (\ sqrt x) ^ 2 = (-1) x = -x.$

Par l'argument donn?? ci-dessus, je peux ??tre ni positif ni n??gatif. Cela cr??e un probl??me: pour le nombre complexe z, nous ne pouvons pas d??finir √ z ??tre la racine carr??e "positive" de z.

Pour chaque nombre complexe non nul z il existe exactement deux num??ros w tel que w ² = z. Par exemple, la racine carr??e de i sont les suivants:

$\ Sqrt {i} = \ frac {1} {\ sqrt {2}} (1 + i)$

$- \ Sqrt {i} = - \ frac {1} {\ sqrt {2}} (1 + i).$

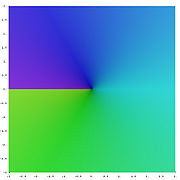
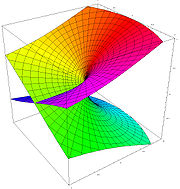
La d??finition habituelle de √ z est en introduisant la suivante Branch Cut: si z = r e ^{i φ} est repr??sent?? en coordonn??es polaires avec -π <φ ≤ π, puis nous avons mis le principale valeur ??

$\ Sqrt {z} = \ sqrt {r} \, e ^ {i \ phi \ over 2}.$

Ainsi d??finie, la fonction de la racine carr??e est holomorphe partout sauf sur les nombres r??els non-positifs (o?? il ne est m??me pas continu). La s??rie ci-dessus Taylor pour √ 1 + x reste valable pour nombres complexes x avec | x | <1.

Lorsque le nombre est en forme rectangulaire de la formule suivante peut ??tre utilis?? pour la valeur du principal:

$\ Sqrt {x + iy} = \ sqrt {\ frac {r + x} {2}} + i \ frac {y} {\ sqrt {2 (r + x)}}$

o??

$r = | x + iy | = \ sqrt {x ^ 2 + y ^ 2}$

est la valeur absolue ou module du nombre complexe, ?? moins que x = - r et y = 0. Remarquez que le signe de la partie imaginaire de la racine est la m??me que le signe de la partie imaginaire du nombre initial. La partie r??elle de la valeur principale est toujours non n??gative.

Notez qu'en raison de la nature discontinue de la fonction de la racine carr??e dans le plan complexe, la loi ZW = √ √ √ z w est pas vrai en g??n??ral. (??quivalente, le probl??me se produit ?? cause de la libert?? dans le choix de la branche La branche choisie peut ou peut ne pas donner l'??galit??;. En fait, le choix de la branche pour la racine carr??e ne doit pas contenir la valeur du √ √ z w du tout , conduisant ?? l'??chec de l'??galit??. Un probl??me similaire appara??t avec le . logarithme complexe et le journal de relation z + w = log log (ZW)) en supposant ?? tort cette loi sous-tend plusieurs ??preuves?? d??fectueux, par exemple la suivante montrant que -1 = 1:

$-1 = I \ cdot i = \ sqrt {-1} \ cdot \ sqrt {-1} = \ sqrt {-1 \ cdot -1} = \ sqrt {1} = 1$

Le troisi??me l'??galit?? ne peut ??tre justifi??e (voir la preuve valide), cependant, il peut ??tre r??gl?? pour ??tre vrai si nous (1) la libert?? de permis dans le choix de la branche ne exigeant plus la racine carr??e principale (d??fini dans le d??but de l'article) implicite dans la notation √ et (2 ) choisir la branche de la racine carr??e de mani??re ?? exclure la valeur 1. Le c??t?? gauche devient soit

$\ Sqrt {-1} \ cdot \ sqrt {-1} = i \ cdot i = -1$

si la branche comprend + i ou

$\ Sqrt {-1} \ cdot \ sqrt {-1} = (- i) \ cdot (-i) = - 1$

si la branche comprend - i, tandis que le c??t?? droit devient

$\ Sqrt {-1 \ cdot -1} = \ sqrt {1} = 1,$

nouveau par le choix de la branche.

Racines carr??es des matrices et des op??rateurs

Si A est un matrice d??finie positive ou l'exploitant, alors il existe justement une matrice d??finie positive ou l'exploitant B avec B ² = A; nous d??finissons alors √ A = B.

Plus g??n??ralement, ?? tous matrice normale ou op??rateur A il existe op??rateurs B normale telle que B ² = A. En g??n??ral, il existe plusieurs de ces op??rateurs B pour chaque A et la fonction de la racine carr??e ne peuvent pas ??tre d??finis pour les op??rateurs normaux de mani??re satisfaisante. Op??rateurs d??finies positives se apparentent ?? des nombres r??els positifs, et les op??rateurs normales se apparentent ?? des nombres complexes.

Racines carr??es principales des 20 premiers entiers positifs

Comme fractions d??cimales non p??riodiques

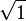
$\ Sqrt {1}$	$= \,$	1
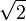
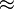
$\ Sqrt {2}$	$\ Approx$	1,4142135623 7309504880 1688724209 6980785696 7187537694 8073176679 7379907324 78462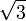
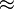
$\ Sqrt {3}$	$\ Approx$	1,7320508075 6887729352 7446341505 8723669428 0525381038 0628055806 9794519330 16909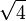
$\ Sqrt {4}$	$= \,$	2
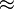
$\ Sqrt {5}$	$\ Approx$	2,2360679774 9978969640 9173668731 2762354406 1835961152 5724270897 2454105209 25638
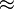
$\ Sqrt {6}$	$\ Approx$	2,4494897427 8317809819 7284074705 8913919659 4748065667 0128432692 5672509603 77457
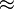
$\ Sqrt {7}$	$\ Approx$	2,6457513110 6459059050 1615753639 2604257102 5918308245 0180368334 4592010688 23230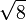
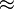
$\ Sqrt {8}$	$\ Approx$	2,8284271247 4619009760 3377448419 3961571393 4375075389 6146353359 4759814649 56924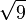
$\ Sqrt {9}$	$= \,$	3
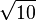
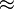
$\ Sqrt {10}$	$\ Approx$	3,1622776601 6837933199 8893544432 7185337195 5513932521 6826857504 8527925944 38639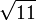
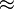
$\ Sqrt {11}$	$\ Approx$	3,3166247903 5539984911 4932736670 6866839270 8854558935 3597058682 1461164846 42609
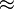
$\ Sqrt {12}$	$\ Approx$	3,4641016151 3775458705 4892683011 7447338856 1050762076 1256111613 9589038660 33818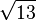
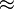
$\ Sqrt {13}$	$\ Approx$	3,6055512754 6398929311 9221267470 4959462512 9657384524 6212710453 0562271669 48293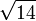
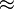
$\ Sqrt {14}$	$\ Approx$	3,7416573867 7394138558 3748732316 5493017560 1980777872 6946303745 4673200351 56307
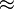
$\ Sqrt {15}$	$\ Approx$	3,8729833462 0741688517 9265399782 3996108329 2170529159 0826587573 7661134830 91937
$\ Sqrt {16}$	$= \,$	4
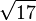
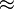
$\ Sqrt {17}$	$\ Approx$	4,1231056256 1766054982 1409855974 0770251471 9922537362 0434398633 5730949543 46338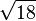
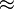
$\ Sqrt {18}$	$\ Approx$	4,2426406871 1928514640 5066172629 0942357090 1562613084 4219530039 2139721974 35386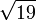
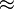
$\ Sqrt {19}$	$\ Approx$	4,3588989435 4067355223 6981983859 6156591370 0392523244 4936890344 1381595573 28203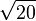
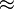
$\ Sqrt {20}$	$\ Approx$	4,4721359549 9957939281 8347337462 5524708812 3671922305 1448541794 4908210418 51276

Comme fractions continues p??riodiques

Un des r??sultats les plus int??ressants de l'??tude des nombres irrationnels que les fractions continues a ??t?? obtenu par Joseph Louis Lagrange vers 1780. Lagrange a constat?? que la racine carr??e d'un nombre entier positif non-carr?? peut ??tre repr??sent?? par un p??riodique fraction continue. Autrement dit, dans lequel un certain motif de chiffres se produit ?? plusieurs reprises dans les d??nominateurs (voir exemple ci-apr??s). Dans un sens, ces racines carr??es sont les plus simples nombres irrationnels, car ils peuvent ??tre repr??sent??s avec un motif r??p??titif simple des chiffres.

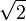
$\ Sqrt {2}$	$= \,$	[1; 2, 2, ...]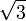
$\ Sqrt {3}$	$= \,$	[1; 1, 2, 1, 2, ...]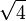
$\ Sqrt {4}$	$= \,$
$\ Sqrt {5}$	$= \,$	[2; 4, 4, ...]
$\ Sqrt {6}$	$= \,$	[2; 2, 4, 2, 4, ...]
$\ Sqrt {7}$	$= \,$	[2; 1, 1, 1, 4, 1, 1, 1, 4, ...]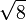
$\ Sqrt {8}$	$= \,$	[2; 1, 4, 1, 4, ...]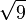
$\ Sqrt {9}$	$= \,$
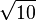
$\ Sqrt {10}$	$= \,$	[3; 6, 6, ...]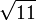
$\ Sqrt {11}$	$= \,$	[3; 3, 6, 3, 6, ...]
$\ Sqrt {12}$	$= \,$	[3; 2, 6, 2, 6, ...]
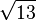
$\ Sqrt {13}$	$= \,$	[3; 1, 1, 1, 1, 6, 1, 1, 1, 1, 6, ...]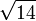
$\ Sqrt {14}$	$= \,$	[3; 1, 2, 1, 6, 1, 2, 1, 6, ...]
$\ Sqrt {15}$	$= \,$	[3; 1, 6, 1, 6, ...]
$\ Sqrt {16}$	$= \,$
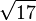
$\ Sqrt {17}$	$= \,$	[4; 8, 8, ...]
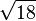
$\ Sqrt {18}$	$= \,$	[4; 4, 8, 4, 8, ...]
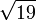
$\ Sqrt {19}$	$= \,$	[4; 2, 1, 3, 1, 2, 8, 2, 1, 3, 1, 2, 8, ...]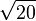
$\ Sqrt {20}$	$= \,$	[4; 2, 8, 2, 8, ...]

La notation de crochet utilis?? ci-dessus est une sorte de raccourci math??matique pour conserver l'espace. ??crit en plus la notation traditionnelle simple fraction continue pour la racine carr??e de 11 - [3; 3, 6, 3, 6, ...] - ressemble ?? ceci:

$\ Sqrt {11} = 3 + \ cfrac {1} {3 + \ cfrac {1} {6 + \ cfrac {1} {3 + \ cfrac {1} {6 + \ cfrac {1} {\ ddots}} }}} \,$

o?? le motif ?? deux chiffres {3, 6} r??p??te encore et encore et encore dans les d??nominateurs partiels.

Construction g??om??trique de la racine carr??e

Une racine carr??e peut ??tre construit avec une r??gle et au compas. Dans ses ??l??ments , Euclide (fl. 300 BC) a donn?? la construction du moyenne g??om??trique des deux quantit??s en deux endroits diff??rents: Proposition II.14 et Proposition VI.13. Depuis la moyenne g??om??trique des a et b est √ ab, on peut construire un √ simplement en prenant b = 1.

La construction est ??galement donn??e par Descartes dans son La G??om??trie, voir figure 2, Cette page 2. Toutefois, Descartes fait aucune r??clamation ?? l'originalit?? et son public aurait ??t?? assez familier avec Euclide.

Une autre m??thode de construction g??om??trique utilise bonnes triangles et induction: √ 1 peut, bien s??r, ??tre construit, et une fois √ x a ??t?? construit, le droit triangle avec 1 et √ x pour ses jambes a une hypot??nuse de √ x + 1.

Histoire

Le Papyrus Math??matique Rhind est une copie de 1650 BC d'une ??uvre encore plus t??t et nous montre comment les Egyptiens extrait des racines carr??es.

Dans l'Inde ancienne , la connaissance des aspects th??oriques et appliqu??s de la racine carr??e et le carr?? ??tait au moins aussi vieux que le Sulba soutras, dat?? autour de 800-500 BC (peut-??tre beaucoup plus t??t). Proc??d?? pour trouver tr??s bonnes approximations ?? la racine carr??e de 2 et 3 sont donn??s dans le Baudhayana Sulba Sutra. Aryabhata dans le Aryabhatiya (section 2.4), a donn?? une m??thode pour trouver la racine carr??e de nombres ayant de nombreux chiffres.

DE Smith dans l'histoire des math??matiques, dit, ?? propos de la situation actuelle en Europe: "En Europe, ces m??thodes (pour trouver le carr?? et la racine carr??e) ne appara??tra pas avant Cataneo (1546). Il a donn?? la m??thode de Aryabhata pour d??terminer la racine carr??e ".

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Square_root&oldid=198942299 "