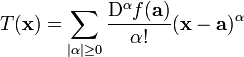S??rie de Taylor
Renseignements g??n??raux
Arrangeant une s??lection Wikipedia pour les ??coles dans le monde en d??veloppement sans internet ??tait une initiative de SOS Enfants. Un lien rapide pour le parrainage d'enfants est http://www.sponsor-a-child.org.uk/

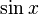 et approximations Taylor, polyn??mes de degr?? 1, 3, 5, 7, 9, 11 et 13.
et approximations Taylor, polyn??mes de degr?? 1, 3, 5, 7, 9, 11 et 13. 
En math??matiques , la s??rie de Taylor est une repr??sentation d'une fonction comme une infinie somme de termes calcul??es ?? partir des valeurs de ses d??riv??s en un seul point. Il peut ??tre consid??r?? comme la limite des polyn??mes de Taylor . S??rie de Taylor sont nomm??s en l'honneur de Math??maticien anglais Brook Taylor. Si la s??rie utilise les d??riv??s ?? z??ro, la s??rie est aussi appel?? une s??rie de Maclaurin, nomm?? d'apr??s Math??maticien ??cossais Colin Maclaurin.
D??finition
La s??rie de Taylor d'un r??el ou complexe fonction f (x) qui est infiniment diff??rentiables dans un voisinage d'un r??el ou complexe d'un nombre, ce est la s??rie de puissance
qui, dans une forme plus compacte peut ??tre ??crit comme
o?? n! est la factorielle de n et f (n) (a) d??signe la ni??me d??riv??e de f au point a; le d??riv?? de z??ro de f est d??fini comme ??tant lui-m??me et f (x - a) et 0 0! sont tous deux d??finis comme une.
Souvent f (x) est ??gale ?? sa s??rie de Taylor ??valu??s ?? x pour tout x assez voisin de a. Ce est la principale raison pour laquelle la s??rie de Taylor sont importants.
Dans le cas particulier o??  , La s??rie est aussi appel?? une s??rie de Maclaurin.
, La s??rie est aussi appel?? une s??rie de Maclaurin.
Exemples
La s??rie de Maclaurin pour tout polyn??me est le polyn??me lui-m??me.
La s??rie de Maclaurin pour  est le s??rie g??om??trique
est le s??rie g??om??trique
de sorte que la s??rie de Taylor pour  ??
?? 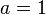 est
est
 .
.
En int??grant le dessus de s??rie de Maclaurin nous trouvons la s??rie de Maclaurin pour 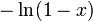 O??
O??  d??signe le logarithme naturel :
d??signe le logarithme naturel :
et la s??rie correspondante pour Taylor  ??
?? 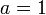 est
est
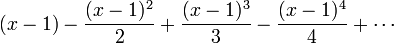 .
.
La s??rie de Maclaurin pour la fonction exponentielle  ??
??  est
est
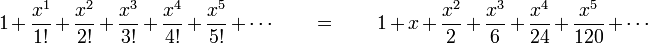 .
.
L'expansion ci-dessus tient parce que le d??riv?? de  est aussi
est aussi  et
et 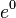 ??gale 1. Cela laisse les termes
??gale 1. Cela laisse les termes 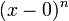 dans le num??rateur et n! dans le d??nominateur pour chaque terme de la somme infinie.
dans le num??rateur et n! dans le d??nominateur pour chaque terme de la somme infinie.
Convergence

La s??rie de Taylor ne doit pas en g??n??ral ??tre un s??rie convergente, mais il est souvent. La limite d'une s??rie convergente Taylor ne doit pas en g??n??ral ??tre ??gale ?? la valeur de la fonction f (x), mais il est souvent. Si f (x) est ??gale ?? sa s??rie de Taylor dans un d'un quartier, il est dit ??tre analytique dans ce quartier. Si f (x) est ??gale ?? sa s??rie de Taylor partout o?? elle est appel??e ensemble. La fonction exponentielle  et les fonctions trigonom??triques sinus et cosinus sont des exemples de fonctions enti??res. Des exemples de fonctions qui ne sont pas ensemble comprennent le logarithme , la fonction trigonom??trique tangente, et son inverse arctan. Pour ces fonctions la s??rie de Taylor ne en ont pas converger si x est loin d'??tre une.
et les fonctions trigonom??triques sinus et cosinus sont des exemples de fonctions enti??res. Des exemples de fonctions qui ne sont pas ensemble comprennent le logarithme , la fonction trigonom??trique tangente, et son inverse arctan. Pour ces fonctions la s??rie de Taylor ne en ont pas converger si x est loin d'??tre une.
Une s??rie de Taylor peut ??tre utilis?? pour calculer la valeur d'une fonction enti??re en tout point, si la valeur de la fonction, et de tous ses d??riv??s, sont connus en un seul point. Usages de la s??rie de Taylor pour les fonctions enti??res comprennent:
- Les sommes partielles (les polyn??mes de Taylor ) de la s??rie peuvent ??tre utilis??s comme approximations de la fonction enti??re. Ces approximations sont bonnes si elles sont suffisamment nombreux termes sont inclus.
- La repr??sentation de la s??rie simplifie de nombreuses preuves math??matiques .
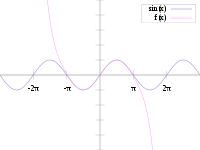
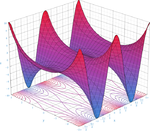
Sur la photo ?? droite est une approximation pr??cise de sin (x) autour du point a = 0. La courbe rose est un polyn??me de degr?? de sept:
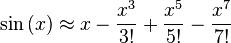 .
.
L'erreur dans cette approximation ne est pas sup??rieure  . En particulier, pour
. En particulier, pour  , L'erreur est inf??rieure ?? 0,000003.
, L'erreur est inf??rieure ?? 0,000003.
En revanche, est ??galement montr?? une image de la fonction log (1 + x) et certains de ses polyn??mes de Taylor autour d'un = 0 Ces approximations convergent vers la fonction que dans la r??gion -1 <x ≤ 1. en dehors de cette r??gion la plus ??lev??e degr?? polyn??mes de Taylor sont des approximations pire pour la fonction. Ceci est un exemple de Ph??nom??ne de Runge.
Le th??or??me de Taylor donne une vari??t?? de limites g??n??rales de la taille de l'erreur dans  engag??s dans l'approximation d'une fonction par son ordre n polyn??me de Taylor.
engag??s dans l'approximation d'une fonction par son ordre n polyn??me de Taylor.
Histoire
Le Philosophe Pythagore Zeno examin?? le probl??me des additionnant une s??rie infinie d'obtenir un r??sultat fini, mais l'a rejet?? comme une impossibilit??: le r??sultat ??tait Le paradoxe de Z??non. Plus tard, Aristote a propos?? une r??solution philosophique du paradoxe, mais le contenu math??matique ??tait apparemment en suspens jusqu'?? repris par D??mocrite et puis Archim??de . Ce est gr??ce ?? Archim??de de m??thode de l'??puisement qu'un nombre infini de subdivisions progressistes pourrait ??tre r??alis??e pour obtenir un r??sultat trigonom??trique finie. Liu Hui employ?? ind??pendamment une m??thode similaire plusieurs si??cles plus tard.
Dans le 14??me si??cle , les premiers exemples de l'utilisation de m??thodes de la s??rie et ??troitement apparent??s ont ??t?? donn??s par Taylor Madhava de Sangamagrama. Bien que aucune trace de son travail survit, ??crits de ult??rieures math??maticiens indiens sugg??rent qu'il a trouv?? un certain nombre de cas particuliers de la s??rie de Taylor, y compris ceux pour les fonctions trigonom??triques de sinus, cosinus, tangente , et arctangente. Le ??cole du Kerala encore ??largi ses ??uvres avec divers d??veloppements en s??rie et approximations rationnelles jusqu'?? ce que le 16??me si??cle .
Dans le 17??me si??cle , James Gregory a ??galement travaill?? dans ce domaine et a publi?? plusieurs s??ries de Maclaurin. Ce ne est que 1715 cependant qu'une m??thode g??n??rale pour la construction de ces s??ries pour toutes les fonctions pour lesquelles ils existent a finalement ??t?? fournis par Brook Taylor, apr??s que les s??ries sont maintenant nomm??s.
La s??rie de Maclaurin a ??t?? nomm?? d'apr??s Colin Maclaurin, professeur ?? Edimbourg, qui a publi?? le cas particulier du r??sultat Taylor dans le 18??me si??cle.
Propri??t??s
Si cette s??rie converge pour tout x dans l'intervalle (a - r, a + r) et la somme est ??gale ?? f (x), alors la fonction f (x) est dit ??tre analytique dans l'intervalle (a - r, a + r). Si cela est vrai pour tout r, alors la fonction est dit ??tre un toute fonction. Pour v??rifier si la s??rie converge vers f (x), on utilise normalement des estimations pour la dur??e du reste du Th??or??me de Taylor . Une fonction est analytique si et seulement si elle peut ??tre repr??sent??e comme une s??rie de puissances ; les coefficients de cette s??rie de puissance sont alors n??cessairement celles indiqu??es dans la formule ci-dessus en s??rie de Taylor.
L'importance d'une telle repr??sentation de la s??rie de puissance est au moins quatre fois. Tout d'abord, la diff??renciation et l'int??gration de la s??rie de puissance peuvent ??tre effectu??es terme ?? terme et est donc particuli??rement facile. Deuxi??mement, un fonction analytique peut ??tre ??tendue ?? un unique fonction holomorphe d??finie sur un disque ouvert dans le plan complexe , ce qui rend l'ensemble des machines analyse complexe disponible. En troisi??me lieu, la s??rie (tronqu??) peut ??tre utilis?? pour calculer des valeurs de fonction environ (souvent par refonte du polyn??me dans la Chebyshev forme et l'??valuation avec le Algorithme Clenshaw).
Quatri??mement, les op??rations alg??briques peuvent souvent ??tre fait beaucoup plus facilement sur la repr??sentation de la s??rie de puissance; par exemple, la preuve la plus simple de La formule d'Euler utilise les d??veloppements en s??rie de Taylor pour sinus, cosinus, et les fonctions exponentielles. Ce r??sultat est d'une importance fondamentale dans des domaines tels que analyse harmonique.
Notez qu'il existe des exemples de fonctions infiniment diff??rentiables f (x) dont la s??rie Taylor convergent, mais ne sont pas ??gale ?? f (x). Par exemple, la fonction ponctuelle d??finie par f (x) = e -1 / m?? x si x ≠ 0 et f (0) = 0 est un exemple d'un fonction lisse non-analytique. Tous ses d??riv??s ?? x = 0 sont ?? z??ro, de sorte que la s??rie de Taylor de f (x) ?? 0 est de z??ro partout, m??me si la fonction ne est pas nul pour tout x ≠ 0. Cette pathologie particuli??re ne afflige pas en s??rie de Taylor analyse complexe. L??, la zone de convergence d'une s??rie de Taylor est toujours un disque dans le plan complexe (??ventuellement avec rayon 0), et o?? la s??rie de Taylor converge, on converge vers la valeur de la fonction. Notez que e -1 / z ?? ne approchez pas 0 en z se approche de 0 long de l'axe imaginaire, d'o?? cette fonction ne est pas continue en fonction sur le plan complexe.
??tant donn?? que chaque s??quence de nombres r??els ou complexes peut appara??tre comme coefficients de la s??rie de Taylor d'une fonction diff??renciable en continu d??fini sur la ligne r??elle, le rayon de convergence d'une s??rie de Taylor peut ??tre ??gal ?? z??ro. Il ya m??me infiniment fonctions diff??rentiables d??finies sur la droite r??elle dont la s??rie Taylor avoir un rayon de convergence 0 partout.
Certaines fonctions ne peuvent pas ??tre ??crit comme s??rie de Taylor parce qu'ils ont un singularit??; dans ces cas, on peut souvent obtenir encore un d??veloppement en s??rie si l'on admet aussi puissances n??gatives de la variable x; voir Laurent s??rie. Par exemple,  peut se ??crire comme une s??rie de Laurent.
peut se ??crire comme une s??rie de Laurent.
Le M??thode Parker-Sochacki est une avanc??e r??cente ?? trouver s??rie de Taylor qui sont des solutions aux ??quations diff??rentielles . Cet algorithme est une extension de la It??ration Picard.
Liste des s??ries de Taylor de certaines fonctions communes
Plusieurs extensions importantes de la s??rie de Maclaurin suivent. Tous ces d??veloppements sont valables pour les arguments complexes 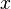 .
.
Fini s??rie g??om??trique:
S??rie g??om??trique infinie:
Des variantes de la s??rie g??om??trique infinie:
S??rie binomiale (comprend la racine carr??e pour α = 1/2 et la s??rie g??om??trique infinie pour α = -1):
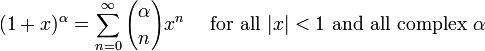
- avec g??n??ralis??es coefficients binomiaux

Les fonctions trigonom??triques :
- o?? le B s sont Nombres de Bernoulli.
Fonctions hyperboliques:
La fonction W de Lambert:
Les nombres  apparaissant dans les expansions de sommation de tan (x) et tanh (x) sont les Nombres de Bernoulli. Le
apparaissant dans les expansions de sommation de tan (x) et tanh (x) sont les Nombres de Bernoulli. Le  dans l'expansion de s (x) sont Nombres d'Euler.
dans l'expansion de s (x) sont Nombres d'Euler.
Calcul de la s??rie de Taylor
Il existe plusieurs m??thodes pour le calcul de la s??rie de Taylor d'un grand nombre de fonctions. On peut tenter d'utiliser la s??rie de Taylor en l'??tat et g??n??raliser la forme des coefficients, ou on peut utiliser des manipulations telles que la substitution, multiplication ou division, addition ou soustraction des s??ries de Taylor standard pour construire la s??rie de Taylor d'une fonction, en vertu de la s??rie Taylor ??tant s??rie de puissance. Dans certains cas, on peut aussi calculer la s??rie de Taylor en appliquant de fa??on r??p??t??e int??gration par parties. Particuli??rement pratique est l'utilisation de syst??mes d'alg??bre informatique pour calculer s??rie de Taylor.
Premier exemple
Calculer la 7 ??me degr?? Maclaurin polynomiale de la fonction
 .
.
Premi??rement, r????crire la fonction comme
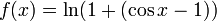 .
.
Nous avons pour le logarithme naturel (en utilisant le notation O grande)
et pour la fonction cosinus
Le d??veloppement en s??rie de celui-ci a un z??ro terme constant, ce qui nous permet de substituer la deuxi??me s??rie dans le premier et d'omettre facilement termes d'ordre plus ??lev?? que le 7 ??me degr?? en utilisant la notation grand O:
Depuis le cosinus est un m??me fonction, les coefficients pour toutes les puissances impaires x, x, x 3 x 5, 7,. . . doivent ??tre de z??ro.
Deuxi??me exemple
Supposons que nous voulons la s??rie de Taylor ?? 0 de la fonction
 .
.
Nous avons pour la fonction exponentielle
et, comme dans le premier exemple,
Supposons que la s??rie de puissance est
Puis multiplication par le d??nominateur et la substitution de la s??rie des rendements de cosinus
Collecte les termes jusqu'?? quatri??me rendements de l'ordre
La comparaison avec les coefficients de la s??rie ci-dessus pour la fonction exponentielle donne la s??rie de Taylor d??sir??
 .
.
S??rie de Taylor que les d??finitions
Classiquement, les fonctions ci-dessus sont d??finis par une propri??t?? qui d??tient pour eux. Par exemple, la fonction exponentielle est d??finie comme ??tant la fonction qui est ??gale ?? sa propre d??riv??. Toutefois, analyse r??cursive, fonctions doit ??tre d??fini par des algorithmes plut??t que des propri??t??s, de sorte que les d??veloppements de Taylor ci-dessus sont utilis??s comme d??finitions primaires plut??t que des r??sultats d??riv??s. Ce est ??galement susceptible d'??tre le cas dans les impl??mentations logicielles des fonctions.
Utilisation s??rie de Taylor, on peut d??finir des fonctions d'analyse des matrices et des op??rateurs, tels que matrice exponentielle ou matrice logarithme.
S??rie de Taylor en plusieurs variables
La s??rie de Taylor peut ??galement ??tre g??n??ralis?? ?? des fonctions de plus d'une variable avec

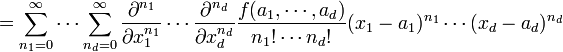 .
.
Par exemple, pour une fonction d??pendant de deux variables x et y, la s??rie de Taylor de deuxi??me ordre par rapport au point (a, b) est:
o?? les indices repr??sentent le respectif d??riv??es partielles.
Un second ordre d??veloppement en s??rie de Taylor d'une fonction scalaire ?? valeur sup??rieure ?? une variable peut ??tre ??crit sous la forme compacte
o??  est le gradient et
est le gradient et  est le Hessien. L'application de la Multi-indice de la s??rie de Taylor pour plusieurs variables devient
est le Hessien. L'application de la Multi-indice de la s??rie de Taylor pour plusieurs variables devient
en pleine analogie avec le cas seule variable.

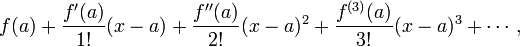






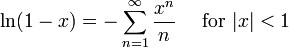
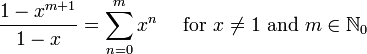
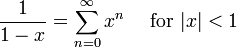
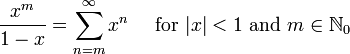

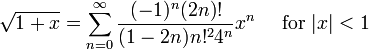
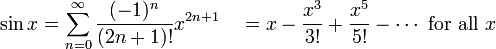
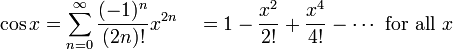

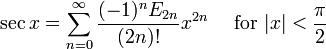

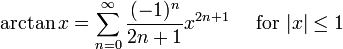




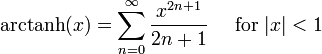
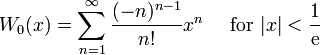

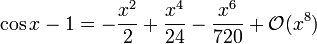

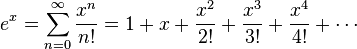

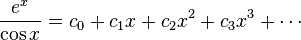

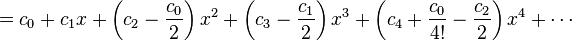
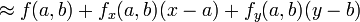
![+ \ Frac {1} {2!} \ Left [f_ {xx} (a, b) (xa) ^ 2 + 2f_ {xy} (a, b) (xa) (YB) + f_ {aa} (un , b) (YB) ^ 2 \ right] \!](../../images/96/9601.png)