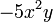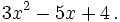Polyn??me

Contexte des ??coles Wikip??dia

SOS croit que l'??ducation donne une meilleure chance dans la vie des enfants dans le monde en d??veloppement aussi. M??res SOS chaque regard apr??s une une famille d'enfants parrain??s .

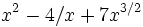En math??matiques , un polyn??me est un expression qui est construit ?? partir d'un ou plusieurs les variables et constantes, en utilisant uniquement les op??rations d'addition, soustraction, multiplication, et constants exposants sont des nombres entiers positifs. Par exemple, $x ^ 2 - 4x + 7 \,$ est un polyn??me, mais $x ^ 2-4 / x + 7x ^ {3/2} \,$ est un polyn??me non parce qu'elle implique la division par une variable et parce qu'il a un exposant qui ne est pas un nombre entier positif.

Polyn??mes sont un des concepts les plus importants de l'alg??bre et dans les math??matiques et les sciences. Ils peuvent ??tre utilis??s pour former des ??quations polynomiales, qui peut coder pour un large ??ventail de probl??mes, de l'??l??mentaire probl??mes de l'histoire ?? des probl??mes complexes dans les sciences; ils peuvent ??tre utilis??s pour d??finir des fonctions polyn??mes, qui apparaissent dans les r??glages de base allant de la chimie et de la physique ?? l'??conomie , et sont utilis??s dans le calcul et analyse num??rique, rapprochant d'autres fonctions. Polyn??mes sont utilis??s dans leur propre droit de construire anneaux de polyn??mes, l'un des concepts les plus puissants de l'alg??bre et de g??om??trie alg??brique.

Vue d'ensemble

Un polyn??me est soit z??ro, ou peut ??tre ??crite comme la somme d'un ou plusieurs non-z??ro termes. Le nombre de termes est fini. Ces termes sont constitu??s d'une constante (appel?? coefficient du terme) multipli?? par z??ro ou plus variables (qui sont g??n??ralement repr??sent??s par des lettres). Chaque variable peut avoir un exposant qui est un entier non n??gatif. L'exposant d'une variable dans une p??riode est ??gale ?? la degr?? de cette variable dans ce terme. Depuis 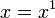$x = x ^ 1$ Le degr?? d'une variable sans exposant est ??crite une. Un terme sans variables est appel?? terme constant, ou tout simplement une constante. Le degr?? d'un terme constant est 0. Le coefficient d'un terme peut ??tre ne importe quel nombre, y compris les fractions, les nombres irrationnels, les nombres n??gatifs, et les nombres complexes.

Par exemple,

$-5x ^ 2a \,$

est un terme. Le coefficient est -5, les variables x et y sont, le degr?? de x est deux, et le degr?? de y est une.

Le degr?? de la dur??e totale est la somme des degr??s de chaque variable en elle. Dans l'exemple ci-dessus, le degr?? est 2 + 1 = 3.

Un polyn??me est une somme de termes. Par exemple, ce qui suit est un polyn??me:

$3x ^ 2 - 5x + 4 \ ,.$

Il se compose de trois termes: le premier est dipl??me de deux, le second est un degr??, et le troisi??me est de z??ro degr??. Ici "

"Signifie"

", De sorte que le coefficient de moyen terme est de -5.

Quand un polyn??me ?? une variable est dispos?? dans l'ordre traditionnel, les termes de degr?? sup??rieur viennent avant les termes de degr?? inf??rieur. Dans le premier terme ci-dessus, le coefficient est de 3, la variable est x, et l'exposant est 2. Dans le second terme, le coefficient est de -5. Le troisi??me terme est une constante. Le degr?? d'un polyn??me non nul est le plus grand degr?? d'une quelconque dur??e. Dans l'exemple, le polyn??me est de degr?? deux.

Autres formes

Une expression qui peut ??tre converti en forme polynomiale ?? travers une s??rie de demandes de l' commutative , associative , et lois de distribution est g??n??ralement consid??r?? comme un polyn??me. Par exemple

$(X + 1) ^ 3$

est un polyn??me, car il peut ??tre ??labor?? ?? 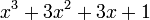$x ^ 3 + 3x ^ 2 + 3x + 1$ . De m??me

$\ Frac {x ^ 3} {12}$

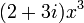est consid??r?? comme un terme de validit?? dans un polyn??me, m??me se il se agit d'une division, parce que ce est l'??quivalent de $\ Frac {1} {12} x ^ 3$ et $\ Frac {1} {12}$ est juste une constante. Le coefficient de ce terme est donc $\ Frac {1} {12}$ . Pour des raisons similaires, si coefficients complexes sont autoris??s, une beaucoup ont un mandat unique comme $(2 + 3i) x ^ 3$ ; m??me si on dirait qu'il devrait ??tre ??labor?? ?? deux mandats, le nombre complexe 2 + 3 i est en fait juste un coefficient unique dans ce cas ce qui se passe ?? exiger un "+" d'??tre ??crit.

Division par une expression contenant une variable est g??n??ralement pas autoris??e dans polyn??mes. Par exemple,

${1 \ over x ^ 2 + 1} \,$

ne est pas un polyn??me car il comprend la division par une variable. De m??me,

$(5 + y) ^ x, \,$

ne est pas un polyn??me, parce qu'il a un exposant variable.

Depuis la soustraction peuvent ??tre trait??s comme ajout de l'additif en face, et, depuis exponentiation ?? une puissance constante de nombre entier positif peut ??tre trait??e comme une multiplication r??p??t??e, polyn??mes peuvent ??tre construits ?? partir des constantes et des variables avec juste l'ajout de deux op??rations et la multiplication.

Fonctions polyn??mes

Une fonction polyn??me est une fonction d??finie par l'??valuation d'un polyn??me. Par exemple, la fonction f, en prenant les nombres r??els pour les nombres r??els, d??fini par

$f (x) = x ^ 3 - x$

est une fonction polynomiale d'une variable. Fonctions polyn??mes peuvent ??galement ??tre d??finis ?? l'aide des polyn??mes en plusieurs variables, comme dans

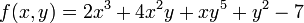$f (x, y) = 2x + 3 ^ 4x ^ xy ^ 2y + 5 + y ^ 7/2$ .

Fonctions polyn??mes sont une classe importante de fonctions lisses.

??quations polynomiales

Une ??quation polynomiale est une ??quation dans laquelle un polyn??me est r??gl?? ??gal ?? un autre polyn??me.

$3x ^ 2 + 4x -5 = 0 \,$

est une ??quation polynomiale.

Propri??t??s ??l??mentaires des polyn??mes

Un somme de polyn??mes est un polyn??me
Un produit de polyn??mes est un polyn??me
Le d??riv?? d'une fonction polynomiale est une fonction polynomiale
Toute primitif ou primitive d'une fonction polynomiale est une fonction polynomiale

Les polyn??mes servent ?? rapprocher d'autres fonctions , telles que sinus, cosinus et exponentielle .

Tous les polyn??mes ont une forme ??largie, dans laquelle le loi distributive a ??t?? utilis?? pour enlever tous les parenth??ses. Toutes les polyn??mes ont ??galement une forme pond??r??e, dans lequel le polyn??me est ??crit comme un produit de polyn??mes lin??aires. Par exemple, le polyn??me

$x ^ 2 - 2x - 3 \,$

est la forme d??velopp??e du polyn??me

$(X - 3) (x + 1) \,$ ,

qui est ??crit sous forme factoris??e. On notera que les constantes de polyn??mes lin??aires (comme -3 et 1 dans l'exemple ci-dessus) peuvent ??tre des nombres complexes dans certains cas.

En alg??bre de l'??cole, les ??l??ves apprennent ?? se d??placer facilement d'une forme ?? l'autre (voir: l'affacturage ).

Chaque polyn??me ?? une variable correspond ?? un polyn??me de la forme

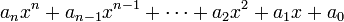$a_n x ^ n + a_ {n-1} x ^ {n-1} + \ cdots + a_2 x ^ 2 + x + a_1 a_0$ .

Cette forme est parfois consid??r?? comme la d??finition d'un polyn??me ?? une variable.

L'??valuation d'un polyn??me consiste ?? attribuer un num??ro ?? chaque variable et l'ex??cution des multiplications et d'additions indiqu??es. ??valuation est parfois effectu?? plus efficace en utilisant Sch??ma de Horner

$((\ Ldots (a_n x + a_ {n-1}) x + ... + a_2) x + a_1) x + a_0 \,$ .

En ??l??mentaire, l'alg??bre , les m??thodes sont donn??s pour r??soudre tous au premier degr?? et du second degr?? ??quations polyn??mes ?? une variable. Dans le cas d'??quations polynomiales, la variable est souvent appel?? une inconnue. Le nombre de solutions ne peut pas d??passer le degr??, et correspondra le degr?? lorsque multiplicit?? des solutions et nombres complexes solutions sont compt??s. Ce fait est appel?? le th??or??me fondamental de l'alg??bre.

Un syst??me d'??quations polynomiales est un ensemble d'??quations dans lequel une variable donn??e doit prendre sur la m??me valeur partout o?? il appara??t dans l'une des ??quations. Syst??mes d'??quations sont g??n??ralement group??es avec une seule accolade ouverte sur la gauche. En alg??bre ??l??mentaire , des proc??d??s sont donn??s pour r??soudre un syst??me d'??quations lin??aires en plusieurs inconnues. Pour obtenir une solution unique, le nombre d'??quations doit ??tre ??gal au nombre d'inconnues. Se il n'y a plus d'inconnues que d'??quations, le syst??me est appel?? sous-d??termin?? . Se il ya plus d'??quations que d'inconnues, le syst??me est appel?? surd??termin??. Ce sujet important est ??tudi?? de fa??on approfondie dans le domaine des math??matiques connues comme l'alg??bre lin??aire . Syst??mes surd??termin??s sont communs dans les applications pratiques. Par exemple, une ??tude cartographique am??ricaine a utilis?? des ordinateurs pour r??soudre 2500000 ??quations 400000 inconnues.

Des exemples plus avanc??s de polyn??mes

En alg??bre lin??aire , le polyn??me caract??ristique d'une matrice carr??e code pour plusieurs propri??t??s importantes de la matrice .

En la th??orie des graphes polyn??me chromatique d'une graphe code les diff??rentes fa??ons de vertex colorer le graphe en utilisant x couleurs.

En alg??bre abstraite , on peut d??finir des polyn??mes ?? coefficients dans toute anneau.

Dans la th??orie des n??uds du Alexander polyn??me, la Polyn??me de Jones, et de la HOMFLY polynomiale sont importants invariants de n??uds.

Histoire

D??terminer les racines de polyn??mes, ou ??la r??solution des ??quations alg??briques", est parmi les plus anciens probl??mes en math??matiques. Toutefois, la notation ??l??gant et pratique que nous utilisons aujourd'hui ne se est d??velopp?? ?? partir du 15??me si??cle. Avant cela, les ??quations sont ??crites dans les mots. Par exemple, un probl??me d'alg??bre des Chinois Arithm??tique en neuf sections, vers 200 avant notre ??re, commence "Trois gerbes de bonne r??colte, deux gerbes de culture m??diocre, et une gerbe de mauvaise r??colte sont vendus pour 29 dou." Nous ??crire 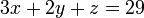$3x + 2y + z = 29$ .

Notation

La premi??re utilisation connue du signe ??gal est en De Robert Recorde Le Whetstone de Witte, 1557. Les signes + pour l'addition, - pour la soustraction, et l'utilisation d'une lettre d'un inconnu apparaissent dans Michael Stifel Arithemetica integra, 1544. Ren?? Descartes, ?? La geometrie, 1637, a introduit le concept de la repr??sentation graphique d'une ??quation polynomiale. Il a popularis?? l'utilisation de lettres ?? partir du d??but de l'alphabet pour d??signer les constantes et les lettres de la fin de l'alphabet pour d??signer les variables, comme on le voit ci-dessus, dans la formule g??n??rale pour un polyn??me ?? une variable, o?? le un ??s d??signent constantes et X repr??sente une variable. Descartes introduit l'utilisation de exposants pour d??signer exposants ainsi.

R??soudre des ??quations polynomiales

Tous les polyn??mes correspond ?? une fonction polynomiale, o?? f (x) est ??gal au polyn??me, et ?? une ??quation polynomiale, o?? le polyn??me est mis ??gal ?? z??ro. Les solutions de l'??quation sont appel??s les racines du polyn??me et ils sont les z??ros de la fonction et les abscisses ?? l'origine de son graphique. Si x = a est une racine d'un polyn??me, alors (x - a) est un facteur de ce polyn??me.

Certains polyn??mes, comme f (x) = x ² + 1, ne ont pas de racines entre les nombres r??els . Cependant, si l'ensemble de candidats admis est ??tendu aux nombres complexes , tout polyn??me (non constante) pr??sente au moins une racine distincte; cela d??coule du th??or??me fondamental de l'alg??bre.

Il existe une diff??rence entre les racines se rapprochant et en trouvant des racines exactes. Formules pour les racines des polyn??mes ?? une degr?? de deux ont ??t?? connu depuis l'Antiquit?? (voir ??quation quadratique ) et jusqu'?? un degr?? de quatre depuis le 16??me si??cle (voir J??r??me Cardan, Niccolo Fontana Tartaglia). Mais les formules de degr?? 5 ??chapp?? chercheurs. En 1824, Niels Henrik Abel prouv?? le r??sultat frappant qu'il ne peut y avoir de formule g??n??rale (comprenant uniquement les op??rations arithm??tiques et les radicaux) pour les racines d'un polyn??me de degr?? 5 ou plus en termes de ses coefficients (voir Th??or??me Abel-Ruffini). Ce r??sultat a marqu?? le d??but de la th??orie de Galois qui se engage dans une ??tude d??taill??e des relations entre les racines de polyn??mes.

R??solvant num??riquement une ??quation polynomiale ?? une inconnue se fait facilement sur l'ordinateur par le Proc??d?? Durand-Kerner ou par un autre root-algorithme de recherche. La r??duction des ??quations dans plusieurs inconnues de chacune des ??quations ?? une inconnue est discut??e dans l'article sur la L'algorithme de Buchberger. Le cas particulier o?? tous les polyn??mes sont de degr?? un est appel?? un syst??me d'??quations lin??aires , pour lesquels une gamme de diff??rentes m??thodes de r??solution existe, y compris le classique ??limination de Gauss .

Il a ??t?? montr?? par Richard Birkeland et Karl Meyr que les racines de tout polyn??me peuvent ??tre exprim??es en termes de multivari??e fonctions hyperg??om??triques. Ferdinand von Lindemann et Hiroshi Umemura a montr?? que les racines peuvent ??galement ??tre exprim??s en termes de Siegel fonctions modulaires, des g??n??ralisations de la th??ta fonctions qui apparaissent dans la th??orie de fonctions elliptiques. Ces caract??risations des racines de polyn??mes arbitraires sont des g??n??ralisations des m??thodes pr??c??demment d??couvert ?? r??soudre le quintique ??quation.

Graphiques

Une fonction polyn??me ?? une variable r??elle peut ??tre repr??sent?? par un graphique.

Le graphe du polyn??me z??ro

f (x) = 0

est l'axe des x.

Le graphique de degr?? 0 polynomiale

f (x) = a _0, o?? un ₀ ≠ 0,

est une ligne horizontale avec ordonn??e ?? l'origine d'un ₀

Le graphique de degr?? 1 polyn??me (ou fonction lin??aire)

f (x) = a ₀ + a ₁ x, o?? a ₁ ≠ 0,

est une ligne oblique avec ordonn??e ?? l'origine d'un ₀ et une pente _1.

Le graphique d'un polyn??me de degr?? 2

f (x) = a ₀ + a ₁ x + a ₂ x ^2, o?? une ₂ ≠ 0

est un parabole.

Le graphique de tout polyn??me de degr?? 2 ou plus

f (x) = a ₀ + a ₁ x + a ₂ x ² +. . . + A _n x ^n, o?? c _n ≠ 0 et n ≥ 2

est une courbe non-lin??aire continu.

Graphiques polyn??mes sont analys??s dans le calcul des intersections, des pentes, concavit??, et le comportement de fin.

Les illustrations ci-dessous montrent les graphiques de polyn??mes.

Polyn??me de degr?? 2: f (x) = x ² - x - 2 = (X 1) (x -2)	Polyn??me de degr?? 3: f (x) = x ^3/4 x 5 + ^2/5-7 x / 5-2 = 1/5 (5 x) (x 1) (x -2)
Polyn??me de degr?? 4: f (x) = 1/14 (x 4) (x 1) (x-1) (x -3) + 0,5	Polyn??me de degr?? 5: f (x) = 1/20 (x 4) (2 x) (x 1) (x-1) (x -3) + 2

Polyn??mes et le calcul

Un aspect important du calcul est le projet de l'analyse des fonctions compliqu??es par les moyens de les rapprocher avec des polyn??mes. Le point culminant de ces efforts est le th??or??me de Taylor , qui stipule que chaque environ fonction diff??rentiable ressemble localement comme un polyn??me, et de la Th??or??me de Stone-Weierstrass, qui stipule que tous les fonction continue d??finie sur un compact intervalle de l'axe r??el peut ??tre approch??e sur tout l'intervalle d'aussi pr??s que souhait?? par un polyn??me. Polyn??mes sont aussi fr??quemment utilis??s pour interpoler fonctions.

Quotients de polyn??mes sont appel??s des expressions rationnelles, et les fonctions qui ??valuent des expressions rationnelles sont appel??s fonctions rationnelles. Fonctions rationnelles sont les seules fonctions qui peuvent ??tre ??valu??es sur un ordinateur par une s??quence fixe d'instructions concernant les op??rations d'addition, multiplication, division, dont les op??rations sur les nombres ?? virgule flottante sont g??n??ralement mises en ??uvre dans mat??riel. Toutes les autres fonctions que les ordinateurs ont besoin pour ??valuer, tels que les fonctions trigonom??triques , logarithmes et exponentielles , doivent alors ??tre calcul??s en logiciel qui peut utiliser des approximations de ces fonctions sur certains intervalles par des fonctions rationnelles, et ??ventuellement it??ration.

Calcul de d??riv??es et int??grales de polyn??mes est particuli??rement simple. Pour le polyn??me

$\ Sum_ {i = 0} ^ n a_i x ^ i$

la d??riv??e par rapport ?? x est

$\ Sum_ {i = 1} ^ n a_i i x ^ {i-1}$

et l'int??grale ind??finie est

$\ Sum_ {i = 0} ^ {n a_i \ over i + 1} x ^ {i + 1} + c$ .

Alg??bre abstraite

En alg??bre abstraite , il faut prendre soin de distinguer entre les polyn??mes et fonctions polyn??mes. Un polyn??me ?? une ind??termin??e 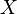$X$ au cours d'une anneau 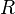$R$ est d??fini comme ??tant une expression formelle de la forme

$f = a_n X ^ n + a_ {n - 1} X ^ {n - 1} + \ cdots + X + a_1 a_0$

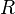o?? $n$ est un nombre naturel, les coefficients $a_0, \ ldots, a_n$ sont des ??l??ments de $R$ et X est consid??r?? comme un symbole formel. Deux polyn??mes partageant la m??me valeur de $n$ sont consid??r??s comme ??gaux si et seulement si les s??quences de leurs coefficients sont ??gaux; En outre, tout polyn??me est ??gal ?? tout polyn??me avec une plus grande valeur de $n$ obtenu d'elle en ajoutant des termes dont le coefficient est ??gal ?? z??ro. Polyn??mes $X$ ?? 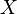coefficients dans 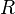$R$ peut ??tre ajout?? en ajoutant simplement coefficients correspondant (la r??gle d'extension par des termes avec coefficients nuls peuvent ??tre utilis??s pour se assurer que ces coefficients existent). Ils peuvent ??tre multipli??s ?? l'aide du loi distributive et la r??gle

$un X ^ k \; b X ^ l = ab X ^ {k + l}$

pour tous les ??l??ments a, b de l'anneau R et tous les num??ros naturelle k et l.

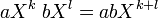
On peut alors v??rifier que l'ensemble de tous les polyn??mes ?? coefficients dans les formes R anneau lui-m??me un anneau, l'anneau des polyn??mes sur R, qui est d??sign??e par R [X]. Si R est commutatif , alors R [X] est un alg??bre sur R.

On peut penser de l'anneau R [X] comme r??sultant de R en ajoutant un nouvel ??l??ment X R et ne n??cessitant que X commutent avec tous les ??l??ments de R. Pour R [X] pour former un noyau, toutes les combinaisons lin??aires de puissances de X doivent ??tre inclus ainsi. Formation de l'anneau de polyn??mes, avec la formation d'anneaux de facteurs par l'affacturage sur id??aux, sont des outils importants pour la construction de nouveaux anneaux de ceux connus. Par exemple, la construction de nettoyage champs finis implique l'utilisation de ces op??rations, en commen??ant avec le champ des entiers modulo certains nombre premier que l'anneau de coefficient R (voir arithm??tique modulaire ).

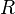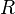Si $R$ est commutatif , alors on peut associer ?? tout polyn??me f $R [X]$ , Une fonction polynomiale avec le domaine et ??gal ?? $R$ (Plus g??n??ralement on peut prendre le domaine et ?? ??tre la m??me unif??re alg??bre associative plus 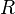$R$ ). On obtient la valeur de cette fonction pour un argument r donn?? par le remplacement, partout le symbole X dans l'expression de f par r. Une raison pour laquelle alg??bristes distinction entre polyn??mes et fonctions polyn??mes est que plus de quelques anneaux diff??rents polyn??mes peuvent donner lieu ?? la m??me fonction polynomiale (voir Le petit th??or??me de Fermat pour un exemple o?? R est entiers modulo p). Ce ne est pas le cas lorsque 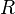$R$ est les nombres r??els ou complexes et donc de nombreux analystes ne ont souvent pas s??parer les deux concepts. Une raison encore plus important de faire la distinction entre les polyn??mes et fonctions polyn??mes est que de nombreuses op??rations sur les polyn??mes (comme Division euclidienne) exige de ce qu'un polyn??me est compos?? comme une expression plut??t que de l'??valuer ?? une certaine valeur constante pour 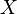$X$ . Et il convient de noter que, si 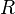$R$ ne est pas commutative, il n'y a pas (bien comport??s) notion de fonction polynomiale du tout.

Divisibilit??

En alg??bre commutative, un point central de l'??tude est la divisibilit?? parmi les polyn??mes. Si R est un domaine et f et g sont des polyn??mes int??grale par R [X], on dit que f divise g se il existe un polyn??me en q R [X] tel que f = g q. On peut alors montrer que ??chaque z??ro donne lieu ?? un facteur lin??aire", ou plus formellement: si f est un polyn??me en R [X] et r est un ??l??ment de R telle que f (r) = 0, alors le polyn??me ( X - r) divise f. L'inverse est ??galement vrai. Le quotient peut ??tre calcul??e en utilisant la Sch??ma de Horner.

Si F est un champ et f et g sont des polyn??mes par F [X] avec g ≠ 0, alors il existe des polyn??mes q et r unique dans F [X] avec

$f = q \, g + r$

et de telle sorte que le degr?? de r est plus petit que le degr?? de g. Le polyn??mes q et r sont d??termin??s de mani??re unique par f et g. Cela se appelle "division avec reste" ou " polynomiale division longue "et montre que l'anneau F [X] est une Domaine euclidienne.

De mani??re analogue, "nombres premiers" polyn??me (plus exactement, polyn??mes irr??ductibles) peut ??tre d??finie, qui ne se factorise en produit de deux polyn??mes de moindre degr??. Il ne est pas facile de d??terminer si un polyn??me irr??ductible est donn??. On peut commencer en v??rifiant simplement si le polyn??me a des facteurs lin??aires. Ensuite, on peut v??rifier la divisibilit?? par d'autres polyn??mes irr??ductibles. Crit??re d'Eisenstein peut ??galement ??tre utilis?? dans certains cas pour d??terminer irr??ductible.

Voir aussi: Plus grand commun diviseur de deux polyn??mes.

Classifications

La classification la plus importante de polyn??mes est bas?? le nombre de variables distinctes. Un polyn??me ?? une variable est appel??e un polyn??me univari??, un polyn??me ?? plusieurs variables est appel?? un polyn??me ?? plusieurs variables. Ces notions se r??f??rent plus au genre de polyn??mes une est g??n??ralement travailler avec que de polyn??mes individuels; par exemple lorsque l'on travaille avec des polyn??mes univari??s une ne exclut pas polyn??mes constants (qui peuvent r??sulter, par exemple, de la soustraction de polyn??mes non constants), bien que strictement parlant polyn??mes constants ne contiennent pas toutes les variables du tout. Il est possible de classer les polyn??mes ?? plusieurs variables en outre que deux variables, ?? trois variables, etc., en fonction du nombre de variables, mais ce est rarement le cas; il est plus fr??quent, par exemple, de dire simplement "polyn??mes en x, y et z". Un (g??n??ralement mulitvariate) est appel?? polyn??me homog??ne de degr?? n si tous ses termes ont degr?? n.

Polyn??mes univari??s ont de nombreuses propri??t??s que ne partagent pas polyn??mes multivari??s. Par exemple, les termes d'un polyn??me univari??e sont compl??tement command??s par leur degr??, et il est classique de toujours ??crire dans un ordre d??croissant de degr??. Un polyn??me univari??e en x de degr?? n prend alors la forme g??n??rale

$c_nx ^ n + c_ {n-1} x ^ {n-1} + \ cdots + c_2x ^ 2 + c_1x + c_0$

o?? c _n, c _n-1, ..., c _2, c ₁ et c ₀ sont des constantes, les coefficients de ce polyn??me. Ici, le terme c _n x ⁿ est appel?? le terme de premier plan et son coefficient c _n le coefficient d'attaque; si le premier coefficient est 1, le polyn??me univari??e est appel?? unitaire. Notez que mis ?? part le premier coefficient c _n (qui doit ??tre diff??rent de z??ro ou encore le polyn??me ne serait pas de degr?? n) cette forme g??n??rale permet de coefficients ?? z??ro; lorsque cela se produit au terme correspondant est ??gal ?? z??ro et peut ??tre retir?? de la somme sans changer le polyn??me. Il est n??anmoins courant de se r??f??rer ?? c _i comme coeffient de x ^i, m??me si c _i arrive ?? 0, de sorte que x ⁱ ne pas vraiment se produire dans ne importe quel terme; par exemple, on peut parler de la terme constant du polyn??me, ce qui signifie c ₀ m??me si elle devrait ??tre de z??ro.

Polyn??mes peuvent ??galement ??tre class??s par le type de valeurs constantes admis en coefficients. On peut travailler avec des polyn??mes ?? coefficients entiers, rationnels, r??els ou complexes, et polyn??mes de l'alg??bre abstraite avec de nombreux autres types de coefficients peuvent ??tre d??finis. Comme pour la classification pr??c??dente, ce est sur les coefficients une fonctionne g??n??ralement avec; par exemple lorsque l'on travaille avec des polyn??mes ?? coefficients complexes comprend une polyn??mes dont les coefficients arriver ?? tout ??tre r??el, m??me si ces polyn??mes peuvent ??galement ??tre consid??r??s comme un des polyn??mes ?? coefficients r??els.

Les polyn??mes peuvent en outre ??tre class??s selon leur degr?? et / ou le nombre de termes non nuls qu'ils contiennent.

Polyn??mes class??e selon le degr??
Degr??	Nom	Exemple
${^ {- \ Infty}}$	z??ro	$0$
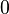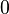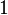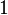$0$	(Non nulle) constante	$1$
$1$	lin??aire	$x + 1$
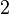$2$	quadratique	$x ^ 2 + 1$
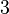$3$	cubique	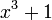$x ^ 3 + 1$
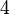$4$	quartique ou biquadratiques	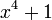$x ^ 4 + 1$
$5$	quintique	$x ^ 5 + 1$
$6$	sextique ou Hexic	$x ^ 6 + 1$
$7$	septique ou heptic	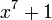$x ^ 7 + 1$
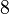$8$	Octic	$x ^ 8 + 1$
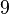$9$	nonic	$x ^ 9 + 1$
$10$	Decic	$x ^ {10} + 1$

Les noms des degr??s plus ??lev??e que 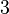$3$ sont moins fr??quentes. Les noms des degr??s peuvent ??tre appliqu??s au polyn??me ou ?? ses termes. Par exemple, une constante peut se r??f??rer ?? un polyn??me de degr?? z??ro ou ?? une peine de z??ro degr??.

Le polyn??me 0, ce qui peut ??tre consid??r?? comme ne pas avoir de termes ?? tout, est appel?? polyn??me z??ro. Contrairement ?? d'autres polyn??mes constants, son degr?? est non nul. Au contraire le degr?? du polyn??me est z??ro soit laiss??e explicitement d??fini, ou d??fini comme ??tant n??gatif (-1 navigateur ou -∞) . La derni??re convention est important lors de la d??finition Division euclidienne des polyn??mes.

Polyn??mes class??s par nombre de termes non nuls
Nombre de termes non nuls	Nom	Exemple
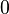$0$	polyn??me z??ro	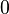$0$
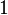$1$	mon??me	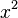$x ^ 2$
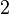$2$	binomial	$x ^ 2 + 1$
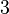$3$	trin??me	$x ^ 2 + x + 1$

Le mot mon??me peut ??tre ambigu??, comme il est ??galement souvent utilis?? pour d??signer simplement une puissance de la variable, ou dans le produit de cas multivari?? de ces pouvoirs, sans coefficient. Deux ou plusieurs termes qui impliquent la m??me mon??me dans ce dernier sens, en d'autres termes, qui ne diff??rent que par la valeur de leurs coefficients, sont appel??s des termes similaires; ils peuvent ??tre combin??s en un seul terme en ajoutant leurs coefficients; si le terme r??sultant a coefficient z??ro, il peut ??tre enti??rement supprim??e. La classification ci-dessus selon le nombre de termes suppose que des termes similaires ont ??t?? combin??s en premier.

Extensions du concept d'un polyn??me

On parle aussi de polyn??mes en plusieurs variables, obtenus en prenant l'anneau des polyn??mes d'un anneau de polyn??mes: R [X, Y] = (R [X]) [Y] = (R [Y]) [X]. Ce sont d'une importance fondamentale dans g??om??trie alg??brique qui ??tudie les simultan??es z??ro ensembles de plusieurs de ces polyn??mes multivari??s.

Polyn??mes sont fr??quemment utilis??s pour encoder des informations sur un autre objet. Le polyn??me caract??ristique d'un op??rateur matriciel ou lin??aire contient des informations sur de l'op??rateur les valeurs propres . Le un polyn??me minimal de ??l??ment alg??brique enregistre la plus simple relation alg??brique satisfait par cet ??l??ment.

Autres objets connexes ??tudi??s dans l'alg??bre abstraite sont s??ries formelles, qui sont comme des polyn??mes mais peut avoir degr?? infini, et de la fonctions rationnelles, qui sont des rapports de polyn??mes.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Polynomial&oldid=198821887 "