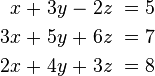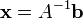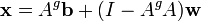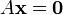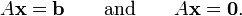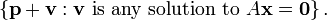Syst??me d'??quations lin??aires
Contexte des ??coles Wikip??dia
SOS Enfants a essay?? de rendre le contenu plus accessible Wikipedia par cette s??lection des ??coles. Les enfants SOS est le plus grand don de charit?? du monde enfants orphelins et abandonn??s la chance de la vie familiale.
En math??matiques , un syst??me d'??quations lin??aires (ou syst??me lin??aire) est une collection de ??quations lin??aires impliquant le m??me ensemble de Variables. Par exemple,
est un syst??me de trois ??quations ?? trois variables x, y, z. Une solution ?? un syst??me lin??aire est une affectation de num??ros ?? des variables telle que toutes les ??quations sont satisfaites simultan??ment. Un solution au syst??me ci-dessus est donn??e par
car elle rend tous les trois ??quations valide.
En math??matiques, la th??orie des syst??mes lin??aires est la base et un ??l??ment fondamental de l'alg??bre lin??aire , un sujet qui est utilis?? dans la plupart des r??gions des math??matiques modernes. Computational algorithmes pour trouver les solutions sont une partie importante de alg??bre lin??aire num??rique, et jouent un r??le de premier plan dans l'ing??nierie , la physique , la chimie , l'informatique et l'??conomie . Un syst??me d'??quations non lin??aires est souvent approch??e par un syst??me lin??aire (voir lin??arisation), une technique utile lors d'un mod??le math??matique ou simulation par ordinateur d'un syst??me relativement complexe.
Tr??s souvent, les coefficients des ??quations sont r??els ou des nombres complexes et les solutions sont recherch??es dans la m??me s??rie de num??ros, mais la th??orie et les algorithmes se appliquent pour les coefficients et les solutions dans toute domaine. Pour les solutions dans un domaine int??grante comme le anneau des entiers , ou dans d'autres structures alg??briques , d'autres th??ories ont ??t?? d??velopp??es. Voir, par exemple, programmation lin??aire pour les solutions enti??res, base de Gr??bner pour polyn??mes coefficients et inconnues, ou encore la g??om??trie tropicale pour l'alg??bre lin??aire dans une structure plus exotique.
Exemple ??l??mentaire
Le type le plus simple du syst??me lin??aire implique deux ??quations et deux variables:
Un proc??d?? pour la r??solution d'un tel syst??me est le suivant. Tout d'abord, r??soudre l'??quation absolue pour  sur le plan de
sur le plan de 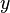 :
:
Maintenant remplacer cette expression pour x dans l'??quation de fond:
Cela se traduit par une seule ??quation impliquant uniquement la variable 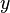 . R??solution donne
. R??solution donne 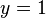 , Et son remplacement par ce retour dans l'??quation pour
, Et son remplacement par ce retour dans l'??quation pour  rendements
rendements  . Cette m??thode se g??n??ralise ?? des syst??mes avec des variables suppl??mentaires (voir ??d'??limination des variables" ci-dessous, ou de l'article sur l'alg??bre ??l??mentaire .)
. Cette m??thode se g??n??ralise ?? des syst??mes avec des variables suppl??mentaires (voir ??d'??limination des variables" ci-dessous, ou de l'article sur l'alg??bre ??l??mentaire .)
Forme g??n??rale
Un syst??me g??n??ral d'??quations m lin??aires ?? n inconnues peut ??tre ??crit comme
Ici 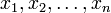 sont les inconnues,
sont les inconnues,  sont les coefficients du syst??me, et
sont les coefficients du syst??me, et 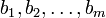 sont les termes constants.
sont les termes constants.
Souvent, les coefficients et les inconnues sont r??els ou des nombres complexes , mais entiers et des nombres rationnels sont ??galement consid??r??s, comme les polyn??mes et les ??l??ments d'un r??sum?? structure alg??brique .
Equation vectorielle
Un point de vue tr??s utile est que chaque inconnu est un poids pour un vecteur colonne dans un combinaison lin??aire.
Cela permet ?? tous la langue et de la th??orie des espaces vectoriels (ou plus g??n??ralement, modules) pour ??tre mises ?? profit. Par exemple, la collecte de toutes les combinaisons lin??aires possibles des vecteurs sur le c??t?? gauche est appel?? leur dur??e, et les ??quations ont une solution juste au moment o?? le vecteur de droite est dans cette p??riode. Si chaque vecteur ?? l'int??rieur de cette s??quence a exactement une expression en tant que combinaison lin??aire des vecteurs de gauche donn??es, toute solution est unique. En tout ??tat de cause, la dur??e a une base de vecteurs lin??airement ind??pendants qui ne garantissent exactement une expression; et le nombre de vecteurs dans cette base (sa dimension) ne peut pas ??tre plus grand que m ou n, mais il peut ??tre plus petite. Ce est important parce que si on a M vecteurs ind??pendants une solution est garantie quel que soit le c??t?? droit, et par ailleurs non garantie.
??quation matricielle
L'??quation vectorielle est ??quivalente ?? une matrice ??quation de la forme
o?? A est une matrice m ?? n, x est un vecteur colonne ?? n entr??es, et b est un vecteur colonne ?? m entr??es.
Le nombre de vecteurs dans une base pour la dur??e est exprim??e en maintenant la rang de la matrice.
jeu de Solution
Une solution d'un syst??me lin??aire est une attribution de valeurs aux variables x 1, x 2, ..., x n de telle sorte que chacune des ??quations est satisfaite. L' ensemble de toutes les solutions possibles est appel?? solution d??finie.
Un syst??me lin??aire peut comporter l'une quelconque des trois mani??res possibles:
- Le syst??me a une infinit?? de solutions.
- Le syst??me a une seule solution unique.
- Le syst??me n'a pas de solution.
Interpr??tation g??om??trique
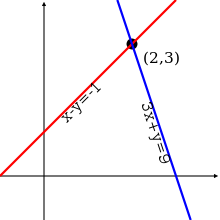
Pour un syst??me impliquant deux variables (x et y), chaque ??quation lin??aire d??termine une ligne sur le xy - plan . Parce que la solution d'un syst??me lin??aire doit satisfaire ?? toutes les ??quations, la solution pr??vue est l' intersection de ces lignes, et est donc soit une ligne, un seul point, ou ensemble vide.
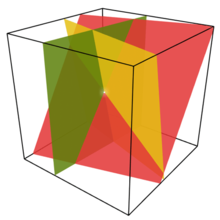
Pour trois variables, chaque ??quation lin??aire d??termine un plan de espace ?? trois dimensions, et l'ensemble de la solution est l'intersection de ces plans. Ainsi l'ensemble de la solution peut ??tre un plan, une ligne, un seul point, ou l'ensemble vide.
Pour n variables, chaque ??quation lin??aire d??termine un hyperplan n l'espace de dimension. L'ensemble de la solution est l'intersection de ces hyperplans, qui peut ??tre un plat de toute dimension.
Comportement g??n??ral

En g??n??ral, le comportement d'un syst??me lin??aire est d??termin??e par la relation entre le nombre d'??quations et le nombre d'inconnues:
- Habituellement, un syst??me avec moins d'??quations que d'inconnues a une infinit?? de solutions ou des solutions rares parfois uniques ( d??tection comprim??). Un tel syst??me est ??galement connu comme un syst??me sous-d??termin??.
- Habituellement, un syst??me ayant le m??me nombre d'??quations et inconnues a une seule solution unique.
- Habituellement, un syst??me avec plus d'??quations que d'inconnues n'a pas de solution. Un tel syst??me est ??galement connu comme un syst??me surd??termin??.
Dans le premier cas, la dimension de l'ensemble de la solution est g??n??ralement ??gal ?? n - m, o?? n est le nombre de variables et m est le nombre d'??quations.
Les images suivantes illustrent cette trichotomie dans le cas de deux variables:

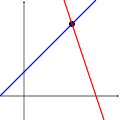
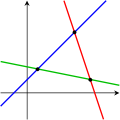
Une ??quation Deux ??quations Trois ??quations
Le premier syst??me a une infinit?? de solutions, ?? savoir tous les points sur la ligne bleue. Le deuxi??me syst??me pr??sente une seule solution unique, ?? savoir l'intersection des deux lignes. Le troisi??me syst??me n'a pas de solution, puisque les trois lignes part aucun point commun.
Gardez ?? l'esprit que les images ci-dessus montrent que le cas le plus commun. Il est possible pour un syst??me de deux ??quations ?? deux inconnues ne pas avoir de solution (si les deux lignes sont parall??les), ou pour un syst??me de trois ??quations ?? deux inconnues pour ??tre solvable (si les trois lignes se croisent en un seul point). En g??n??ral, un syst??me d'??quations lin??aires peut se comporter diff??remment que pr??vu si les ??quations sont lin??airement d??pendante, ou si deux ou plusieurs des ??quations sont incompatibles .
Propri??t??s
Ind??pendance
Les ??quations du syst??me lin??aire sont ind??pendants si aucun des ??quations peut ??tre d??riv?? alg??briquement des autres. Lorsque les ??quations sont ind??pendantes, chaque ??quation contient de nouvelles informations sur les variables, et en supprimant l'une des ??quations augmente la taille de l'ensemble de la solution. Pour ??quations lin??aires, l'ind??pendance logique est le m??me que ind??pendance lin??aire.
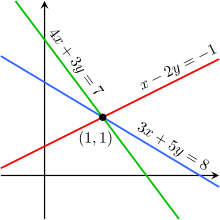
Par exemple, les ??quations
ne sont pas ind??pendants - ils sont la m??me ??quation lorsque l'??chelle par un facteur de deux, et ils seraient produire des graphiques identiques. Ceci est un exemple d'??quivalence dans un syst??me d'??quations lin??aires.
Pour un exemple plus compliqu??, les ??quations
ne sont pas ind??pendants, car la troisi??me ??quation est la somme des deux autres. En effet, l'une quelconque de ces ??quations peuvent ??tre d??riv??es ?? partir des deux autres, et l'une quelconque des ??quations peut ??tre retir?? sans affecter l'ensemble de la solution. Les graphiques de ces ??quations sont trois lignes qui se croisent en un seul point.
Coh??rence

Un syst??me lin??aire est conforme si elle a une solution, et incompatible contraire. Lorsque le syst??me est incoh??rent, il est possible de d??river un contradiction ?? partir des ??quations, qui peuvent toujours ??tre r????crits comme la d??claration 0 = 1.
Par exemple, les ??quations
sont incompatibles. En effet, en soustrayant la premi??re ??quation ?? partir de la seconde et en multipliant les deux c??t??s du r??sultat par 1/6, on obtient 0 = 1. Les graphiques de ces ??quations sur la Plane xy sont une paire de des lignes parall??les.
Il est possible pour les trois ??quations lin??aires sont incompatibles, m??me si deux d'entre elles sont compatibles ensemble. Par exemple, les ??quations
sont incompatibles. En ajoutant les deux premi??res ??quations ensemble donne 3 x 2 + y = 2, qui peut ??tre soustraite de la troisi??me ??quation pour obtenir 0 = 1. Notez que deux de ces ??quations ont une solution commune. Le m??me ph??nom??ne peut se produire pour un certain nombre d'??quations.
En g??n??ral, les incoh??rences se produisent si les c??t??s gauche des ??quations dans un syst??me sont lin??airement d??pendants, et les termes constants ne r??pondent pas ?? la relation de d??pendance. Un syst??me d'??quations dont les c??t??s gauche sont lin??airement ind??pendants est toujours coh??rente.
En d'autres mots, selon la Rouch??-Capelli th??or??me, tout syst??me d'??quations (surd??termin?? ou autre) est incompatible si le rang de la matrice augment??e est plus grande que le rang de la matrice de coefficients. Si, d'autre part, les rangs de ces deux matrices sont ??gales, le syst??me doit avoir au moins une solution. La solution est unique si et seulement si le rang est ??gal au nombre de variables. Sinon, la solution g??n??rale a k param??tres libres o?? k est la diff??rence entre le nombre de variables et le rang; par cons??quent, dans un tel cas, il existe une infinit?? de solutions.
??quivalence
Deux syst??mes lin??aires utilisant le m??me ensemble de variables sont ??quivalentes si chacune des ??quations du second syst??me peut ??tre d??riv??e ?? partir des ??quations alg??briques dans le premier syst??me, et vice-versa. Deux syst??mes sont ??quivalentes si l'une ou les deux sont incompatibles chaque ??quation de l'un d'eux est une combinaison lin??aire des ??quations de l'autre. Il se ensuit que deux syst??mes lin??aires sont ??quivalentes si et seulement si ils ont le m??me ensemble de solutions.
R??solution d'un syst??me lin??aire
Il existe plusieurs algorithmes pour r??soudre un syst??me d'??quations lin??aires.
D??crivant la solution
Lorsque l'ensemble de la solution est fini, il est r??duit ?? un seul ??l??ment. Dans ce cas, l'unique solution est d??crite par une s??quence d'??quations dont la main gauche c??t??s sont les noms des inconnues et les c??t??s de la main droite sont les valeurs correspondantes, par exemple 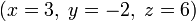 . Quand une commande sur les inconnues a ??t?? fix??, par exemple, le ordre alphab??tique la solution peut ??tre d??crit comme un vecteur de valeurs, comme
. Quand une commande sur les inconnues a ??t?? fix??, par exemple, le ordre alphab??tique la solution peut ??tre d??crit comme un vecteur de valeurs, comme 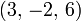 pour l'exemple pr??c??dent.
pour l'exemple pr??c??dent.
Il peut ??tre difficile de d??crire un ensemble avec une infinit?? de solutions. En r??gle g??n??rale, certaines des variables sont d??sign??s comme libre (ou ind??pendant, ou en tant que param??tres), ce qui signifie qu'ils peuvent prendre ne importe quelle valeur, tandis que les variables restantes sont fonction des valeurs des variables libres.
Par exemple, consid??rons le syst??me suivant:
La solution mis ?? ce syst??me peut ??tre d??crit par les ??quations suivantes:
Ici z est la variable libre, tandis que x et y d??pendent de z. Ne importe quel point dans le jeu de solution peut ??tre obtenue en choisissant une premi??re valeur de z, puis en calculant les valeurs correspondantes de x et y.
Chaque variable libre donne l'une de l'espace de solution degr?? de libert??, dont le nombre est ??gal ?? la dimension de l'ensemble de la solution. Par exemple, la solution pr??vue pour l'??quation ci-dessus est une ligne, depuis un point dans l'ensemble de la solution peut ??tre choisi en sp??cifiant la valeur du param??tre z. Une solution infinie d'ordre sup??rieur peut d??crire un avion, ou un ensemble de plus grande dimension.
Des choix diff??rents pour les variables libres peuvent conduire ?? des descriptions d'un m??me ensemble de la solution. Par exemple, la solution aux ??quations ci-dessus peut en variante ??tre d??crit comme suit:
Ici, la variable x est libre, et y et z sont d??pendants.
??limination des variables
La m??thode la plus simple pour r??soudre un syst??me d'??quations lin??aires est d'??liminer des variables ?? plusieurs reprises. Cette m??thode peut ??tre d??crite comme suit:
- Dans la premi??re ??quation, pour r??soudre l'une des variables en fonction des autres.
- Branchez cette expression dans les ??quations restantes. Cela donne un syst??me d'??quations avec un de moins ??quation et un de moins inconnue.
- Continuez jusqu'?? ce que vous avez r??duit le syst??me ?? une seule ??quation lin??aire.
- R??solvez cette ??quation, puis sauvegarder substitut jusqu'?? ce que toute solution soit trouv??e.
Par exemple, consid??rons le syst??me suivant:
R??solution de la premi??re ??quation donne pour x = x 2 + z 5 - 3 y, et de brancher ce dans les deuxi??me et troisi??me rendements ??quation
. R??solution de la premi??re de ces ??quations pour les rendements y y = 2 + 3 z, et de brancher ce dans les secondes rendements ??quation z = 2 Nous avons maintenant:
En substituant z = 2 dans la deuxi??me ??quation donne y = 8, et son remplacement par z = 2 et y = 8 dans les premiers rendements de l'??quation x = -15. Par cons??quent, l'ensemble de la solution est le point (x, y, z) = unique (-15, 8, 2).
la r??duction de la rang??e
En mati??re de r??duction de ligne, le syst??me lin??aire est pr??sent??e comme une matrice augment??e:
Cette matrice est ensuite modifi?? ?? l'aide op??rations ??l??mentaires sur les lignes jusqu'?? ce qu'il atteigne forme r??duite de Gauss. Il ya trois types d'op??rations ??l??mentaires sur les lignes:
- Type 1: ??changer les positions de deux rang??es.
- Type 2: Multipliez une rang??e par un non nulle scalaire.
- Type 3: Ajouter ?? une ligne un multiple scalaire d'un autre.
??tant donn?? que ces op??rations sont r??versibles, la matrice augment??e produite repr??sente toujours un syst??me lin??aire qui est ??quivalente ?? l'original.
Il ya plusieurs algorithmes sp??cifiques pour r??duire une rang??e matrice augment??e, dont la plus simple est l'??limination de Gauss et ??limination de Gauss-Jordan. Le calcul suivant montre l'??limination de Gauss-Jordan appliqu??e ?? la matrice ci-dessus:
La derni??re matrice est sous forme r??duite de Gauss, et repr??sente le syst??me x = -15, y = 8, z = 2. Une comparaison avec l'exemple dans la section pr??c??dente sur l'??limination alg??brique des variables montre que ces deux m??thodes sont en fait le m??me; la diff??rence r??side dans la fa??on dont les calculs sont ??crites.
La r??gle de Cramer
La r??gle de Cramer est une formule explicite pour la solution d'un syst??me d'??quations lin??aires, ?? chaque variable donn??e par un quotient de deux d??terminants . Par exemple, la solution du syst??me
est donn??e par
Pour chaque variable, le d??nominateur est le d??terminant de la matrice de coefficients, alors que le num??rateur est le d??terminant d'une matrice dans laquelle une colonne a ??t?? remplac?? par le vecteur de termes constants.
Bien que la r??gle de Cramer est important en th??orie, il a peu de valeur pratique pour les grandes matrices, depuis le calcul des grands d??terminants est un peu lourd. (En effet, les grands d??terminants sont le plus facilement calcul?? en utilisant la r??duction de la ligne.) En outre, la r??gle de Cramer poss??de des propri??t??s num??riques tr??s pauvres, le rendant impropre ?? r??soudre m??me les petits syst??mes de fa??on fiable, ?? moins que les op??rations sont effectu??es en arithm??tique rationnelle avec une pr??cision infinie.
solution de matrice
Si le syst??me d'??quation est exprim??e sous la forme d'une matrice 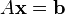 , L'ensemble de la solution peut ??galement ??tre exprim?? sous forme de matrice. Si la matrice A est carr??e (a m lignes et n = m colonnes) et a rang plein (toutes les lignes de m sont ind??pendants), le syst??me a une solution unique donn??e par
, L'ensemble de la solution peut ??galement ??tre exprim?? sous forme de matrice. Si la matrice A est carr??e (a m lignes et n = m colonnes) et a rang plein (toutes les lignes de m sont ind??pendants), le syst??me a une solution unique donn??e par
o?? 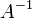 est le inverse de A. Plus g??n??ralement, ind??pendamment du fait que m = n ou non, et quel que soit le rang de A, toutes les solutions (se il en existe) sont donn??s en utilisant le Pseudo-inverse de A, not??e
est le inverse de A. Plus g??n??ralement, ind??pendamment du fait que m = n ou non, et quel que soit le rang de A, toutes les solutions (se il en existe) sont donn??s en utilisant le Pseudo-inverse de A, not??e  , Comme suit:
, Comme suit:
o?? 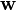 est un vecteur de param??tres libres qui se ??tend sur toute possible n ?? 1 vecteurs. Une condition n??cessaire et suffisante pour que ne importe quelle solution (s) d'exister, ce est que la solution obtenue ?? l'aide potentielle
est un vecteur de param??tres libres qui se ??tend sur toute possible n ?? 1 vecteurs. Une condition n??cessaire et suffisante pour que ne importe quelle solution (s) d'exister, ce est que la solution obtenue ?? l'aide potentielle 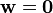 satisfaire
satisfaire 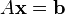 - ?? savoir que
- ?? savoir que 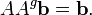 Si cette condition ne est pas v??rifi??e, le syst??me d'??quations est incoh??rente et n'a pas de solution. Si la condition est v??rifi??e, le syst??me est conforme et au moins une solution existe. Par exemple, dans le cas mentionn?? ci-dessus dans laquelle A est carr??e et de plein rang,
Si cette condition ne est pas v??rifi??e, le syst??me d'??quations est incoh??rente et n'a pas de solution. Si la condition est v??rifi??e, le syst??me est conforme et au moins une solution existe. Par exemple, dans le cas mentionn?? ci-dessus dans laquelle A est carr??e et de plein rang,  ??gale tout simplement
??gale tout simplement 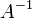 et l'??quation de la solution g??n??rale se simplifie en
et l'??quation de la solution g??n??rale se simplifie en 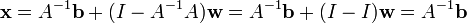 comme indiqu?? pr??c??demment, o??
comme indiqu?? pr??c??demment, o?? 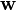 a compl??tement abandonn?? la solution, ne laissant qu'une seule solution. Dans d'autres cas, cependant,
a compl??tement abandonn?? la solution, ne laissant qu'une seule solution. Dans d'autres cas, cependant, 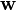 reste et donc une infinit?? de valeurs potentielles du vecteur de param??tre libre
reste et donc une infinit?? de valeurs potentielles du vecteur de param??tre libre 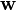 donner une infinit?? de solutions de l'??quation.
donner une infinit?? de solutions de l'??quation.
D'autres m??thodes
Alors que les syst??mes de trois ou quatre ??quations peuvent ??tre facilement r??solus par la main, les ordinateurs sont souvent utilis??s pour des syst??mes plus grands. L'algorithme standard pour r??soudre un syst??me d'??quations lin??aires est bas??e sur l'??limination de Gauss avec quelques modifications. Tout d'abord, il est essentiel pour ??viter la division par un petit nombre, qui peuvent conduire ?? des r??sultats erron??s. Cela peut ??tre fait en r??ordonnant les ??quations si n??cessaire, un processus connu sous le nom pivotement. Deuxi??mement, l'algorithme ne fait pas exactement ??limination de Gauss, mais il calcule la LU d??composition de la matrice A. Ce est surtout un outil d'organisation, mais il est beaucoup plus rapide si l'on doit r??soudre plusieurs syst??mes avec la m??me matrice A, mais diff??rents vecteurs b.
Si la matrice A a une structure sp??ciale, ce qui peut ??tre exploit??e pour obtenir des algorithmes plus rapides ou plus pr??cises. Par exemple, les syst??mes ??quip??s d'un sym??trique matrice d??finie positive peut ??tre r??solu deux fois plus vite avec le D??composition de Cholesky. R??currence de Levinson est une m??thode rapide pour Matrices de Toeplitz. M??thodes sp??ciales existent ??galement pour les matrices avec de nombreux ??l??ments z??ro (soi-disant matrices creuses), qui apparaissent souvent dans les applications.
Une approche totalement diff??rente est souvent prise pour de tr??s grands syst??mes, qui, autrement, prendre trop de temps ou de la m??moire. L'id??e est de commencer avec une premi??re approximation de la solution (qui ne doit pas ??tre exacts ?? tous), et de changer cette approximation en plusieurs ??tapes pour se rapprocher de la vraie solution. Une fois que l'approximation est suffisamment pr??cise, ce est consid??r?? comme ??tant la solution au syst??me. Cela conduit ?? la classe de m??thodes it??ratives.
Syst??mes homog??nes
Un syst??me d'??quations lin??aires est homog??ne si toutes les conditions sont constantes z??ro:
Un syst??me homog??ne est ??quivalente ?? une ??quation de la forme de la matrice
o?? A est une matrice m ?? n, x est un vecteur colonne ?? n entr??es, et 0 est le vecteur nul avec des entr??es de m.
jeu de Solution
Chaque syst??me homog??ne pr??sente au moins une solution, dite solution z??ro (ou solution triviale), qui est obtenu en affectant la valeur de z??ro pour chacune des variables. Si le syst??me poss??de une matrice non singuli??re (det (A) ≠ 0), alors il est aussi la seule solution. Si le syst??me poss??de un matrice singuli??re alors il ya un ensemble de solutions avec un nombre infini de solutions. Cet ensemble de solutions a les propri??t??s suppl??mentaires suivantes:
- Si u et v sont deux vecteurs repr??sentant des solutions ?? un syst??me homog??ne, alors la somme de vecteur u + v est ??galement une solution au syst??me.
- Si u est un vecteur repr??sentant une solution ?? un syst??me homog??ne, et R est tout scalaire, alors R u est aussi une solution au syst??me.
Ce sont exactement les propri??t??s requises pour la solution ??tabli pour ??tre la sous-espace lin??aire de R n. En particulier, la solution r??gl?? ?? un syst??me homog??ne est le m??me que le espace nul de la matrice A correspondant.
Rapport aux syst??mes non homog??nes
Il existe une relation ??troite entre les solutions d'un syst??me lin??aire et les solutions du syst??me homog??ne correspondant:
Plus pr??cis??ment, si p est une solution particuli??re au syst??me lin??aire Ax = b, alors l'ensemble de la solution peut ??tre d??crit comme
G??om??triquement, cela dit que l'ensemble de la solution A x = b est un traduction de l'ensemble de la solution A x = 0. Plus pr??cis??ment, le plat pour le premier syst??me peut ??tre obtenu par la traduction de la sous-espace lin??aire pour le syst??me homog??ne par le vecteur p.
Ce raisonnement ne se applique que si le syst??me A x = b a au moins une solution. Cela se produit si et seulement si le vecteur b se situe dans la image de la Une transformation lin??aire.

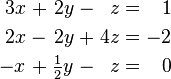
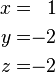
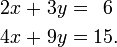


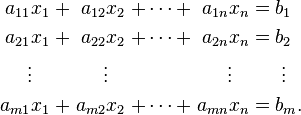
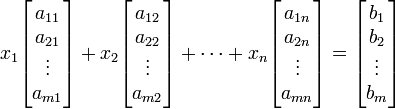
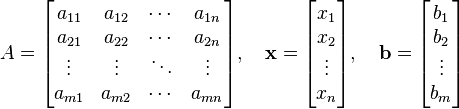
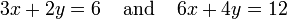
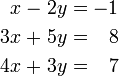



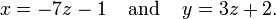


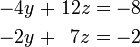
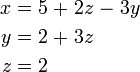
![\ Left [\ begin {array} {rrr | r} 1 & 3 & -2 et 5 \\ 3 & 5 & 6 & 7 \\ 2 & 4 & 3 & 8 \ end {array} \ right] \ text { .}](../../images/1643/164330.png)
![\ Begin {align} \ left [\ begin {array} {rrr | r} 1 & 3 & -2 et 5 \\ 3 & 5 & 6 & 7 \\ 2 & 4 & 3 & 8 \ end {array} \ droite] et \ sim \ left [\ begin {array} {rrr | r} 1 & 3 & 5 -2 et 0 \\ & -4 et 12 -8 \\ & 2 & 4 & 3 & 8 \ end {array } \ right] \ sim \ left [\ begin {array} {rrr | r} 1 & 3 & 5 -2 et 0 \\ & -4 et 12 -8 et \\ 0 et -2 et 7 & -2 \ end {array} \ right] \ sim \ left [\ begin {array} {rrr | r} 1 & 3 & 5 -2 et \\ 0 & 1 & 2 -3 et 0 \\ & -2 et 7 et - 2 \ end {array} \ right] \\ & \ sim \ left [\ begin {array} {rrr | r} 1 & 3 & 5 -2 et \\ 0 & 1 & 2 -3 et \\ 0 & 0 & 1 & 2 \ end {array} \ right] \ sim \ left [\ begin {array} {rrr | r} 1 & 3 & 5 -2 et \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \ end {array} \ right] \ sim \ left [\ begin {array} {rrr | r} 1 & 3 & 0 & 0 9 \\ & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \ end {array} \ right] \ sim \ left [\ begin {array} {rrr | r} 1 & 0 & 0 et -15 \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \ end {array} \ right]. \ end {align}](../../images/1643/164331.png)