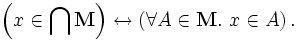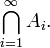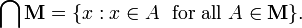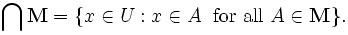Intersection (th??orie des ensembles)
Contexte des ??coles Wikip??dia
Les articles de cette s??lection ??coles ont ??t?? organis??s par sujet du programme d'??tudes gr??ce aux b??n??voles d'enfants SOS. parrainage SOS enfant est cool!
En math??matiques , l'intersection de deux ensembles A et B est l'ensemble qui contient tous les ??l??ments de A qui appartiennent ??galement ?? B (ou de mani??re ??quivalente, tous les ??l??ments de B qui appartiennent ??galement ?? A), mais pas d'autres ??l??ments.
Pour l'explication des symboles utilis??s dans cet article, reportez-vous ?? la table des symboles math??matiques.
D??finition de base

L'intersection de A et B est ??crit "A ∩ B". Formellement:
- x est un ??l??ment de A ∩ B si et seulement si
- x est un ??l??ment de A et
- x est un ??l??ment de B.
- Par exemple:
- L'intersection des ensembles {1, 2, 3} et {2, 3, 4} {est 2, 3}.
- Le num??ro 9 ne est pas dans l'intersection de l'ensemble des nombres premiers {2, 3, 5, 7, 11, ...} et l'ensemble des {nombres impairs 1, 3, 5, 7, 9, 11, ...}.
Si l'intersection de deux ensembles A et B est vide, ce est qu'ils ne ont pas d'??l??ments en commun, ils sont cens??s ??tre disjoints, not??e: A ∩ B = ??. Par exemple, les ensembles {1, 2} et {3, 4} sont disjoints, ??crits
{1, 2} ∩ {3, 4} = ??.
Plus g??n??ralement, on peut prendre l'intersection de plusieurs ensembles ?? la fois. L'intersection de A, B, C et D, par exemple, est A ∩ B ∩ C ∩ D = A ∩ (B ∩ (C ∩ D)). Intersection est un associative op??ration; ainsi,
A ∩ (B ∩ C) = (A ∩ B) ∩ C.
Intersections arbitraires
La notion la plus g??n??rale est l'intersection d'une collection d'ensembles non vide arbitraire. Si M est une non vide dont les ??l??ments sont eux-m??mes fixe, alors x est un ??l??ment de l'intersection de M si et seulement si pour chaque ??l??ment A de M, x est un ??l??ment de A. Dans symboles:
Cette id??e englobe les paragraphes ci-dessus, en ce que, par exemple, A ∩ B ∩ C est l'intersection de la collection {A, B, C}.
La notation pour cette derni??re notion peut varier consid??rablement. R??glez th??oriciens seront parfois ??crire "∩ M", tandis que d'autres seront plut??t ??crire ??∩ A ∈ M A". Cette derni??re notation peut ??tre g??n??ralis??e ?? "i ∈ I ∩ A i", qui se r??f??re ?? l'intersection de la collection {A i: i ∈ I}. Voici I est un ensemble non vide, et A i est un ensemble pour chaque i dans I.
Dans le cas o?? le ensemble d'indices I est l'ensemble des nombres naturels , vous pouvez voir la notation analogue ?? celle d'un s??rie infinie:
Lorsque le formatage est difficile, cela peut ??galement ??tre ??crit "A 1 A 2 ∩ ∩ ∩ A 3 ...", m??me si ?? proprement parler, A 1 ∩ (A 2 ∩ (A 3 ∩ ... n'a pas de sens. (Ce dernier exemple, une intersection de d??nombrable de nombreux ensembles, est en fait tr??s commun; pour un exemple, voir l'article sur σ-alg??bres.)
Enfin, notons que chaque fois que le symbole ??∩?? est plac?? avant les autres symboles ?? la place de entre eux, il devrait ??tre de plus grande taille (⋂).
Intersection nulaires
Notez que dans la section pr??c??dente, nous avons exclu le cas o?? M est la ensemble vide (∅). La raison en est la suivante. L'intersection de la collection M est d??fini comme l'ensemble (voir notation ensemble constructeur)
Si M est vide, il n'y a pas de s??ries A dans M, la question devient "laquelle x 's satisfaire la condition ??nonc??e?" La r??ponse semble ??tre tout x possible. Lorsque M est vide la condition donn??e ci-dessus est un exemple d'un la v??rit?? vide. Alors l'intersection de la famille devrait ??tre vide "l'ensemble de tout". Le probl??me est, il n'y a pas tel ensemble. En supposant un tel ensemble existe conduit ?? un probl??me c??l??bre la th??orie des ensembles na??ve connu sous le nom Le paradoxe de Russell. Pour cette raison, l'intersection de l'ensemble vide ne est pas d??finie.
Un correctif partielle ?? ce probl??me peut ??tre trouv??e si nous sommes d'accord pour restreindre notre attention sur des sous-ensembles d'un ensemble fixe appel?? le U univers. Dans ce cas, l'intersection d'une famille de sous-ensembles de U peut ??tre d??finie comme
Maintenant, si M est vide, il ne ya aucun probl??me. L'intersection est juste de tout l'univers U, qui est un bien d??fini fix?? par hypoth??se.