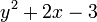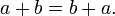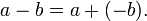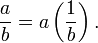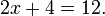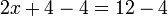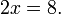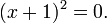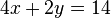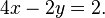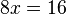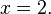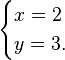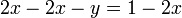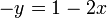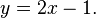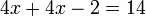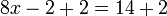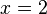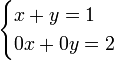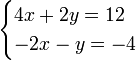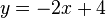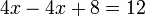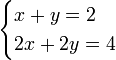Alg??bre ??l??mentaire
Contexte des ??coles Wikip??dia
SOS Enfants, qui se d??roule pr??s de 200 sos ??coles dans le monde en d??veloppement, a organis?? cette s??lection. Un lien rapide pour le parrainage d'enfants est http://www.sponsor-a-child.org.uk/
Alg??bre ??l??mentaire est une forme fondamentale et relativement de base de l'alg??bre enseign??e aux ??tudiants qui sont pr??sum??s avoir peu ou pas de connaissance formelle de math??matiques au-del?? de l'arithm??tique . Alors que seulement en arithm??tique num??ros et leurs op??rations arithm??tiques (tels que +, -, ??, ??) se produisent, en alg??bre on utilise aussi des symboles (tels que x et y, ou a et b) pour d??signer les num??ros. Ils sont appel??s Variables. Ce est utile parce que:
- Il permet la g??n??ralisation des arithm??tiques ??quations (et in??galit??s ) ??tre ??nonc??s comme des lois (comme
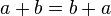 pour tout a et b), et est donc la premi??re ??tape pour l'??tude syst??matique des propri??t??s du syst??me des nombres r??els .
pour tout a et b), et est donc la premi??re ??tape pour l'??tude syst??matique des propri??t??s du syst??me des nombres r??els . - Il permet de faire r??f??rence ?? des num??ros qui ne sont pas connus. Dans le contexte d'un probl??me, une variable peut repr??senter une certaine valeur est incertaine, mais peut ??tre r??solu gr??ce ?? la formulation et la manipulation d'??quations.
- Il permet l'exploration des relations math??matiques entre les quantit??s (tels que "si vous vendez x billets, alors votre b??n??fice sera
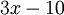 dollars ??).
dollars ??).
Ces trois sont les principaux axes de l'alg??bre ??l??mentaire, qui doit ??tre distingu??e de l'alg??bre abstraite , un sujet plus avanc?? g??n??ralement enseign??e aux ??tudiants de niveau coll??gial.
En alg??bre ??l??mentaire, un " . expression ??peut contenir des nombres, des variables et des op??rations arithm??tiques Ceux-ci sont g??n??ralement ??crites (par convention) avec des termes?? plus grande puissance ??sur la gauche (voir polynomiale ); quelques exemples:
En alg??bre plus avanc??, une expression peut ??galement inclure fonctions ??l??mentaires.
Un ?? ??quation ??est l'affirmation que deux expressions sont ??gales. Quelques ??quations sont vraies pour toutes les valeurs des variables impliqu??es (comme 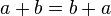 ); ces ??quations sont appel??s " "." identit??s ??quations conditionnelles ??sont vraies que pour certaines valeurs des variables concern??es:
); ces ??quations sont appel??s " "." identit??s ??quations conditionnelles ??sont vraies que pour certaines valeurs des variables concern??es: 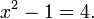 Les valeurs des variables qui rendent l'??quation vraie sont appel??s les ??solutions?? de l'??quation.
Les valeurs des variables qui rendent l'??quation vraie sont appel??s les ??solutions?? de l'??quation.
Lois de l'alg??bre ??l??mentaire
- Commutative propri??t?? de plus
- Soustraction est l'inverse de l'addition.
- Pour soustraire est le m??me que pour ajouter un nombre n??gatif :
- Exemple: si
 puis
puis 
- Commutativit?? de la multiplication
- Division est l'inverse de la multiplication.
- Pour fracture est le m??me que pour multiplier par un r??ciproque:
- Exponentiation ne est pas une op??ration commutative.
- Par cons??quent exponentiation a une paire de op??rations inverses: logarithme et exponentielle avec des exposants fractionnaires (par exemple des racines carr??es ).
- Exemples: si
 puis
puis  Si
Si 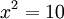 puis
puis 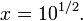
- Exemples: si
- Les racines carr??es de nombres n??gatifs ne existent pas dans le syst??me des nombres r??els. (Voir: syst??me de nombre complexe )
- Par cons??quent exponentiation a une paire de op??rations inverses: logarithme et exponentielle avec des exposants fractionnaires (par exemple des racines carr??es ).
- Associatif propri??t?? de plus:

- Associativit?? de la multiplication:

- Distributivit?? de la multiplication par rapport ?? l'addition:

- Distributivit?? de la exponentiation ?? l'??gard de la multiplication:
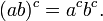
- Comment combiner les exposants:

- Puissance ?? une propri??t?? de puissance d'exposants:
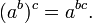
Lois de l'??galit??
- Si
 et
et 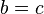 , Puis
, Puis  ( transitivit?? de l'??galit??).
( transitivit?? de l'??galit??).  ( r??flexivit?? de l'??galit??).
( r??flexivit?? de l'??galit??). - Si
 puis
puis  ( la sym??trie de l'??galit??).
( la sym??trie de l'??galit??).
Autres lois
- Si
 et
et  puis
puis 
- Si
 puis
puis 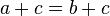 pour tout c (propri??t?? de plus d'??galit??).
pour tout c (propri??t?? de plus d'??galit??).
- Si
- Si
 et
et  puis
puis 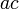 =
= 
- Si
 puis
puis 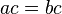 pour tout c (propri??t?? de multiplication de l'??galit??).
pour tout c (propri??t?? de multiplication de l'??galit??).
- Si
- Si deux symboles sont ??gaux, alors on peut ??tre substitu?? ?? l'autre ?? volont?? (principe de substitution).
- Si
 et
et 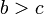 puis
puis  (Transitivit?? de l'in??galit??).
(Transitivit?? de l'in??galit??). - Si
 puis
puis  pour ne importe quel c.
pour ne importe quel c. - Si
 et
et 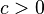 puis
puis 
- Si
 et
et 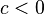 puis
puis 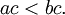
Exemples
??quations lin??aires ?? une variable
Les ??quations sont plus simples ?? r??soudre des ??quations lin??aires qui ont une seule variable. Ils ne contiennent que des nombres constants et une seule variable sans exposant. Par exemple:
La technique centrale est d'ajouter, soustraire, multiplier ou diviser les deux c??t??s de l'??quation par le m??me nombre afin d'isoler la variable d'un c??t?? de l'??quation. Une fois que la variable est isol??e, de l'autre c??t?? de l'??quation est la valeur de la variable. Par exemple, en soustrayant 4 des deux c??t??s de l'??quation ci-dessus:
ce qui simplifie ??:
Divisant les deux c??t??s par deux:
simplifie ?? la solution:
Le cas g??n??ral,
suit le m??me format pour la solution:
??quations du second degr??
??quations du second degr?? peuvent ??tre exprim??es sous la forme ax 2 + bx + c = 0, o?? a est de z??ro (si ce ??tait z??ro, l'??quation ne serait pas mais quadratique lin??aire ). Pour cette raison une ??quation quadratique doit contenir le terme hache 2, qui est connu comme le terme quadratique. Ainsi a ≠ 0, et ainsi nous pouvons diviser par un et r??organiser l'??quation dans le formulaire standard
o?? p = b / a et q = - c / a. R??soudre ce, par un proc??d?? connu sous le nom compl??tant le carr??, conduit ?? la formule quadratique .
??quations du second degr?? peuvent ??galement ??tre r??solus en utilisant factorisation (le processus inverse de ce qui est l'expansion, mais pour deux termes lin??aires sont parfois not??s dorure). A titre d'exemple de factorisation:
Qui est la m??me chose que
Il r??sulte de ce propri??t?? z??ro produit qui soit x = 2 ou x = -5 sont les solutions, car pr??cis??ment l'un des ??l??ments doit ??tre ??gal ?? z??ro . Tous les ??quations du second degr?? auront deux solutions dans le nombre complexe syst??me, mais ne doivent pas n??cessairement avoir un dans le nombre r??el syst??me. Par exemple,
n'a pas de solution de nombre r??el puisque aucun nombre r??el carr?? est ??gal ?? -1. Parfois, une ??quation quadratique a une racine de multiplicit?? 2, tels que:
Pour cette ??quation, -1 est une racine de multiplicit?? 2.
Syst??me d'??quations lin??aires
Dans le cas d'un syst??me d'??quations lin??aires , comme, par exemple, deux ??quations ?? deux variables, il est souvent possible de trouver les solutions de ces deux variables qui satisfont les deux ??quations.
Premi??re m??thode de trouver une solution
Un exemple d'un syst??me d'??quations lin??aires peut ??tre le suivant:
Multipliant les termes de la deuxi??me ??quation par 2:
En ajoutant les deux ??quations, pour obtenir:
ce qui simplifie ??
Puisque le fait que x = 2 est connue, il est alors possible d'en d??duire que y = 3 par l'une des deux ??quations originales (en utilisant ?? la place de x 2) La solution compl??te ?? ce probl??me consiste alors
Notez que ce ne est pas la seule fa??on de r??soudre ce syst??me sp??cifique; y auraient pu ??tre r??solus avant x.
Deuxi??me m??thode de trouver une solution
Une autre fa??on de r??soudre le m??me syst??me d'??quations lin??aires est effectu??e par substitution.
Un ??quivalent de y peut ??tre d??duite ?? l'aide de l'une des deux ??quations. Utilisation de la deuxi??me ??quation:
En soustrayant 2x ?? partir de chaque c??t?? de l'??quation:
et en multipliant par -1:
En utilisant cette valeur de y dans la premi??re ??quation dans le syst??me d'origine:
Ajout de deux de chaque c??t?? de l'??quation:
ce qui simplifie ??
En utilisant cette valeur dans l'une des ??quations, la m??me solution que dans la m??thode pr??c??dente est obtenue.
Notez que ce ne est pas la seule fa??on de r??soudre ce syst??me sp??cifique; dans ce cas aussi, y aurait pu ??tre r??solus avant x.
D'autres types de syst??mes d'??quations lin??aires
Syst??mes insolubles
Dans l'exemple ci-dessus, il est possible de trouver une solution. Toutefois, il existe ??galement des syst??mes d'??quations qui ne ont pas de solution. Un exemple ??vident serait:
La deuxi??me ??quation dans le syst??me n'a pas de solution possible. Par cons??quent, ce syst??me ne peut pas ??tre r??solu. Cependant, tous les syst??mes incompatibles sont reconnus ?? premi??re vue. A titre d'exemple, le syst??me est ??tudi??e ci-dessous:
En essayant de r??soudre ce (par exemple, en utilisant le proc??d?? de substitution ci-dessus), la seconde ??quation, apr??s addition de - 2 x sur les deux c??t??s et en multipliant par -1, a pour r??sultat:
Et en utilisant cette valeur de y dans la premi??re ??quation:
Aucune variable sont ?? gauche, et l'??galit?? ne est pas vrai. Cela signifie que la premi??re ??quation ne peut pas fournir une solution pour la valeur de y obtenu dans la deuxi??me ??quation.
Syst??mes ind??termin??es
Il existe ??galement des syst??mes qui ont plusieurs solutions ou infinis, par opposition ?? un syst??me avec une solution unique (sens, deux valeurs uniques pour x et y) Par exemple:
Isolement de y dans la deuxi??me ??quation suivante:
Et l'utilisation de cette valeur dans la premi??re ??quation dans le syst??me:
L'??galit?? est vrai, mais il ne fournit pas de valeur pour x. En effet, on peut facilement v??rifier (en remplissant simplement dans certaines valeurs de x) que pour tout x il existe une solution tant que y = -2 x + 6. Il ya une infinit?? de solutions pour ce syst??me.
Au-Systems sousd??termin??s
Syst??mes avec plus de variables que le nombre d'??quations lin??aires ne ont pas de solution unique. Un exemple d'un tel syst??me est
Un tel syst??me est appel?? sous-d??termin??; en essayant de trouver une solution, une ou plusieurs variables ne peuvent ??tre exprim??es par rapport aux autres variables, mais ne peuvent ??tre d??termin??es num??riquement. Par ailleurs, un syst??me avec un plus grand nombre d'??quations que de variables, dont certaines ??quations n??cessairement des sommes ou des multiples d'autres, est appel?? surd??termin??.
Relation entre Solvabilit?? et Multiplicit??
Compte tenu de tout syst??me d'??quations lin??aires, il ya une relation entre la multiplicit?? et la solvabilit??.
Si une ??quation est une multiple de l'autre (ou, plus g??n??ralement, un somme des multiples des autres ??quations), le syst??me d'??quations lin??aires est ind??termin??e, ce qui signifie que le syst??me a une infinit?? de solutions. Exemple:
Lorsque la multiplicit?? ne est que partielle (ce qui signifie que, par exemple, seuls les c??t??s de gauche de l'??quation sont des multiples, tandis que les c??t??s de droite ne sont pas ou pas par le m??me nombre), puis le syst??me est insoluble. Par exemple, dans
les secondes rendements ??quation que x + y = 1/4 qui est en contradiction avec la premi??re ??quation. Un tel syst??me est incompatible aussi appel?? dans le langage de l'alg??bre lin??aire . Lorsque vous essayez de r??soudre un syst??me d'??quations lin??aires, il est g??n??ralement une bonne id??e de v??rifier si une ??quation est un multiple de l'autre. Si tel est pr??cis??ment l'affirmative, la solution ne peut pas ??tre d??termin??e de fa??on unique. Si ce ne est que partiellement, ne existe pas la solution.
Ceci, cependant, ne signifie pas que les ??quations doivent ??tre des multiples les uns des autres pour avoir une solution, comme indiqu?? dans les sections ci-dessus; en d'autres termes: la multiplicit?? dans un syst??me d'??quations lin??aires est pas un condition n??cessaire pour la solvabilit??.