Soustraction

"5-2 = 3" (verbalement, "cinq moins deux ??galent trois??)

Un exemple de probl??me

En arithm??tique , la soustraction est l'un des quatre de base op??rations binaires; ce est l'inverse de plus , ce qui signifie que si nous commen??ons par ne importe quel nombre et d'ajouter ne importe quel nombre et puis soustraire le m??me nombre, nous avons ajout??, nous revenons au nombre nous avons commenc?? avec. La soustraction est not??e par un moins vous connecter notation infixe, contrairement ?? l'usage du signe de plus pour plus.

Depuis la soustraction ne est pas un commutative op??rateur, les deux op??randes sont nomm??s. Les noms traditionnels pour les parties de la formule

c - b = a

sont diminuende (c) - ?? soustraire (b) = diff??rence (a).

La soustraction est utilis?? pour mod??liser quatre processus connexes:

1. Provenant d'une collection donn??e, enlever (soustraire) un nombre donn?? d'objets. Par exemple, 5 les pommes moins deux feuilles de pommes 3 pommes.
2. Partir d'une mesure donn??e, enlever une quantit?? mesur??e dans les m??mes unit??s. Si je p??se 200 livres, et de perdre 10 livres, alors je p??se 200-10 = ?? 190.
3. Comparer deux quantit??s comme pour trouver la diff??rence entre eux. Par exemple, la diff??rence entre 800 $ et 600 $ est de 800 $ - $ 600 = $ 200. Aussi connu comme la soustraction comparative.
4. Pour trouver la distance entre deux endroits ?? une distance fixe du point de d??part. Par exemple, si, sur une route donn??e, vous voyez un marqueur de kilom??trage qui dit 150 miles et voir plus tard, un marqueur de kilom??trage qui dit 160 miles, vous avez voyag?? 160-150 = 10 miles.

En math??matiques , il est souvent utile pour afficher ou m??me d??finir la soustraction comme une sorte de plus , l'ajout de la Oppos??. Nous pouvons voir 7-3 = 4 comme la somme des deux Conditions: 7 et -3. Cette perspective nous permet d'appliquer ?? la soustraction de toutes les r??gles connues et la nomenclature de l'addition. Soustraction ne est pas associative ou commutative fait -in, il est anticommutative et ?? gauche associative, mais plus de nombres sign??s est ?? la fois.

Soustraction de base: entiers

Imaginez un segment de ligne de longueur b avec l'extr??mit?? gauche ??tiquet?? et l'extr??mit?? droite ??tiquet?? c. A partir d'un, il faut b pas ?? droite pour atteindre c. Ce mouvement vers la droite est mod??lis?? math??matiquement par ailleurs :

a + b = c.

De c, il faut b ??tapes vers la gauche pour revenir ?? un. Ce mouvement vers la gauche est mod??lis?? par soustraction:

c - b = a.

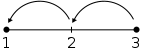
Maintenant, un segment de ligne marqu?? avec le nombre 1 , 2, et 3. Dans la position 3, il ne prend aucune mesure ?? la gauche de rester ?? 3, donc 3-0 = 3. Il faut deux ??tapes vers la gauche pour arriver ?? la position 1, donc 3-2 = 1. Cette image est insuffisante pour d??crire ce qui se passerait apr??s avoir trois ??tapes vers la gauche de la position 3. Pour repr??senter une telle op??ration, la ligne doit ??tre ??tendue.

Pour soustraire arbitraires nombres naturels , on commence par une ligne contenant toutes les nombre naturel (0, 1, 2, 3, 4, 5, 6, ...). De trois, il faut trois ??tapes vers la gauche pour se rendre ?? 0, donc 3-3 = 0. Mais 3-4 est toujours pas valide car il laisse ?? nouveau la ligne. Les nombres naturels ne sont pas un contexte utile pour la soustraction.

La solution consiste ?? consid??rer le nombre entier droite num??rique (..., -3, -2, -1, 0, 1, 2, 3, ...). De trois, il faut quatre ??tapes vers la gauche pour arriver ?? -1:

3-4 = -1.

Soustraction que l'addition

Il ya certains cas o?? la soustraction en tant qu'entit?? distincte op??ration devient probl??matique. Par exemple, 3 - (-2) (c.-?? soustraire -2 de 3) ne est pas imm??diatement ??vident ?? partir d'un nombre naturel vue ou une vue sur la ligne de nombre, car il ne est pas imm??diatement clair ce que cela signifie de se d??placer -2 ??tapes vers la gauche ou ?? emporter -2 pommes. Une solution consiste ?? voir la soustraction que l'addition des nombres sign??s. Signes moins suppl??mentaires simplement d??notent inversion additive. Ensuite, nous avons 3 - (-2) = 3 + 2 = 5. Cela contribue aussi ?? maintenir la anneau des entiers "simple" en ??vitant l'introduction de "nouveaux" op??rateurs tels que la soustraction. Ordinairement un anneau n'a que deux op??rations d??finies sur elle; dans le cas des nombres entiers, ce sont des additions et des multiplications. Une bague a d??j?? le concept des inverses additifs, mais il n'a aucune notion d'une op??ration de soustraction s??par??e, donc l'utilisation de plus sign?? que la soustraction nous permet d'appliquer les axiomes de sonner pour la soustraction sans avoir besoin de prouver quoi que ce soit.

Algorithmes pour la soustraction

Il existe diff??rents algorithmes de soustraction, et ils diff??rent dans leur aptitude ?? des applications vari??es. Un certain nombre de m??thodes sont adapt??s pour calculer ?? la main ; par exemple, lors de changement, pas de soustraction r??elle est effectu??e, mais plut??t le changement fabricant compte avant.

Pour le calcul de la machine, la Proc??d?? de compl??ments est pr??f??r??, dans lequel la soustraction est remplac??e par une addition en une arithm??tique modulaire.

L'enseignement dans les ??coles de la soustraction

Les m??thodes utilis??es pour enseigner soustraction ??cole ??l??mentaire varie de pays ?? pays, et dans un pays, diff??rentes m??thodes sont ?? la mode ?? des moments diff??rents. Dans ce qui est, dans le US , appel?? math??matiques traditionnelles, un processus sp??cifique est enseign?? aux ??tudiants ?? la fin de la 1??re ann??e ou au cours de la 2e ann??e pour une utilisation avec des nombres entiers ?? plusieurs chiffres, et se prolonge dans la quatri??me ou ?? la cinqui??me ann??e d'inclure des repr??sentations d??cimales de nombres fractionnaires.

Certaines ??coles am??ricaines enseignent actuellement une m??thode de soustraction ?? l'aide d'emprunt et un syst??me de marquage appel?? b??quilles. M??me si une m??thode d'emprunt avait ??t?? connu et publi?? dans les manuels avant, apparemment, les b??quilles sont l'invention de William A. Brownell qui les utilise dans une ??tude en Novembre 1937. Ce syst??me pris sur rapidement, d??pla??ant les autres m??thodes de soustraction en usage dans Am??rique ?? ce moment-l??.

Certaines ??coles europ??ennes emploient une m??thode de soustraction appel?? la m??thode autrichienne, aussi connu comme la m??thode des ajouts. Il n'y a pas emprunt dans ce proc??d??. Il ya aussi des b??quilles (marques pour aider la m??moire), qui varient selon les pays.

Ces deux m??thodes briser la soustraction comme un processus de soustractions ?? un chiffre par la valeur de position. A partir d'un chiffre le moins significatif, une soustraction de diminuteur:

s _j s _{j -1 1} ... S

de diminuende

m _{k k} m _-1 m ... _1,

o?? chaque _i et M S _i est un chiffre, produit en ??crivant m ₁ - s _{1, 2} m - s _2, et ainsi de suite, tant que s _i ne exc??de pas m _i. Sinon, m _i est augment?? de 10 et quelques autres chiffres est modifi?? pour corriger cette augmentation. Proc??d?? am??ricain corrige en tentant de r??duire le chiffre diminuende m _{i une} par une (ou de continuer la retenue vers la gauche jusqu'?? ce qu'il y est un chiffre non nul ?? partir de laquelle d'emprunter). La m??thode europ??enne corrige en augmentant _{la i} du diminuteur chiffres _une par une.

Exemple: 704 - 512. Le diminuende est 704, le diminuteur est 512. Les chiffres sont diminuende m ₃ = 7, m ₂ = 0 et m = ₁ 4. Les chiffres sont ?? soustraire s ₃ = 5, S ₂ = 1 et s ₁ = 2. Commen??ant ?? la place de l'une, quatre ne est pas moins de 2 sorte que la diff??rence 2 est ??crit dans le r??sultat de un seul endroit. ?? la place de dix, 0 est inf??rieur ?? 1, de sorte que le 0 est port?? ?? 10, et la diff??rence avec une, qui est neuf, est ramen??e ?? la place de dix. La m??thode am??ricaine corrige pour l'augmentation de dix en r??duisant le chiffre des centaines de la place de la diminuende par un. Ce est, le 7 est barr?? et remplac?? par un 6. La soustraction proc??de alors ?? la place des centaines, o?? 6 ne est pas inf??rieur ?? 5, de sorte que la diff??rence est ??crit dans de centaines de la place du r??sultat. Nous sommes maintenant fait, le r??sultat est de 192.

Proc??d?? autrichien ne r??duit pas la 7 ?? 6. Au contraire, il augmente le chiffre des centaines par une soustraction. Une petite marque est faite ?? proximit?? ou en dessous de ce chiffre (en fonction de l'??cole). Puis la soustraction produit par demander ce num??ro lorsque augment?? de 1, et 5 est ajout?? ?? elle, fait 7. La r??ponse est 1, et est ??crit dans de centaines de la place du r??sultat.

Il ya une subtilit?? suppl??mentaire que l'??tudiant utilise toujours une table de soustraction mentale dans la m??thode am??ricaine. La m??thode autrichienne encourage souvent l'??l??ve ?? utiliser mentalement la table d'addition dans le sens inverse. Dans l'exemple ci-dessus, plut??t que d'ajouter 1-5, obtenant 6, et en soustrayant que de 7, l'??tudiant est invit?? ?? examiner ce nombre, lorsqu'il a augment?? de 1, et 5 est ajout?? ?? elle, fait 7.

Unit??

En retranchant deux num??ros avec des unit??s, ils doivent avoir la m??me unit??. Dans la plupart des cas, la diff??rence aura la m??me unit?? que le nombre d'origine. Une exception est quand la soustraction de deux chiffres avec le pourcentage que l'unit??. Dans ce cas, la diff??rence devra points de pourcentage comme unit??.