
Arithm??tique
Saviez-vous ...
Cette s??lection ??coles a ??t?? choisi par SOS Enfants pour les ??coles dans le monde en d??veloppement ne ont pas acc??s ?? Internet. Il est disponible en t??l??chargement intranet. Pour comparer les organismes de bienfaisance de parrainage ce est le meilleur lien de parrainage .

Arithm??tique ou arithm??tique (du grec mot ἀριθμός, arithmos " nombre ") est la branche la plus ancienne et la plus ??l??mentaire de math??matiques , utilis?? par presque tout le monde, pour des t??ches allant du simple au jour le jour ?? compter avanc??es scientifiques et commerciales calculs. Il se agit de l'??tude de la quantit?? , d'autant plus que le r??sultat des op??rations qui combinent num??ros. Dans l'usage courant, il se r??f??re aux propri??t??s simples en utilisant la traditionnelle op??rations de plus , la soustraction , la multiplication et la division avec de plus petites valeurs de nombres. Professionnels math??maticiens utilisent parfois le terme (sup??rieur) arithm??tique en se r??f??rant ?? des r??sultats plus avanc??s li??s ?? la th??orie des nombres , mais cela ne devrait pas ??tre confondus avec l'arithm??tique ??l??mentaire .
Histoire
La pr??histoire de l'arithm??tique est limit??e ?? un petit nombre d'objets qui peut indiquer la conception de l'addition et la soustraction, le plus connu ??tant le b??ton d'Ishango de l'Afrique centrale , datant de quelque part entre 20 000 et 18 000 en Colombie-Britannique, bien que son interpr??tation est contest??e.
Les premiers documents ??crits indiquent la Egyptiens et Babyloniens utilisaient toutes les op??rations arithm??tiques ??l??mentaires d??s 2000 BC. Ces artefacts ne r??v??lent pas toujours le processus sp??cifique utilis?? pour r??soudre les probl??mes, mais les caract??ristiques du particulier syst??me de num??ration influencent fortement la complexit?? des m??thodes. Le syst??me hi??roglyphique Chiffres ??gyptiens, comme les ult??rieures chiffres romains , les descendants de marques de pointage utilis??s pour le comptage. Dans les deux cas, cette origine a donn?? lieu ?? des valeurs qui utilisaient une virgule base, mais ne comprend pas notation positionnelle. Des calculs complexes avec chiffres romains besoin de l'aide d'un conseil ou le comptage Abacus romaine pour obtenir les r??sultats.
Les premiers syst??mes num??riques qui comprenait notation de position ne ??taient pas d??cimal, y compris le sexag??simal (base 60) syst??me de Chiffres babyloniennes et le vig??simal syst??me (base 20) qui a d??fini Num??ration maya. En raison de ce concept de valeur de, la possibilit?? de r??utiliser les m??mes chiffres pour diff??rentes valeurs a contribu?? ?? des m??thodes de calcul plus simples et plus efficaces.
Le d??veloppement historique continue de l'arithm??tique moderne commence par la La civilisation hell??nistique de la Gr??ce antique, m??me si elle provient beaucoup plus tard que les Babyloniens et les exemples ??gyptiens. Avant les ??uvres d' Euclide autour de 300 avant JC, ??tudes grecques en math??matiques chevauchent avec les croyances philosophiques et mystiques. Par exemple, Nicomaque a r??sum?? le point de vue de la premi??re Approche de Pythagore pour les num??ros et leurs relations les uns aux autres, dans son Introduction ?? l'arithm??tique.
Chiffres grecs, d??riv??es du syst??me ??gyptien hi??ratique, manquaient ??galement de notation de position, et donc impos??es la m??me complexit?? sur les op??rations de base de l'arithm??tique. Par exemple, l'ancien math??maticien Archim??de a consacr?? toute son travail L'Ar??naire simplement ?? l'??laboration d'une notation pour un certain grand nombre entier.
Le d??veloppement progressif de Chiffres indo-arabes con??us ind??pendamment du concept de valeur de position et la notation, qui combine les m??thodes plus simples pour les calculs avec une base d??cimal et l'utilisation d'un chiffre repr??sentant z??ro . Cela a permis au syst??me de repr??senter toujours petits et grands entiers. Cette approche finalement remplac?? tous les autres syst??mes. Au d??but du 6e si??cle de notre ??re, le math??maticien indien Aryabhata incorpor?? une version existante de ce syst??me dans son travail, et a exp??riment?? avec diff??rentes notations. Au 7??me si??cle, Brahmagupta ??tabli l'utilisation de z??ro en tant que num??ro s??par?? et d??termin?? les r??sultats de multiplication, division, addition et la soustraction de z??ro et tous les autres num??ros, sauf pour le fait de division par z??ro. Son contemporain, le ??v??que syriaque S??v??re Seb??kht d??crit l'excellence de ce syst??me comme ??... des m??thodes de calcul de valeur qui d??passent description". Les Arabes aussi appris cette nouvelle m??thode et l'a appel?? hesab.

Bien que le Chronique d'Albelda d??crit une forme pr??coce de chiffres arabes (en omettant z??ro) par 976 AD, Fibonacci ??tait principalement responsable de la diffusion de leur utilisation dans toute l'Europe apr??s la publication de son livre Liber Abaci en 1202. Il a consid??r?? l'importance de cette "nouvelle" repr??sentation des nombres, qui qu'il appelait la ??m??thode des Indiens?? (latin Modus Indorum), si fondamental que tous li??s fondements math??matiques, y compris les r??sultats de Pythagore et de la algorism d??crivant les m??thodes pour effectuer des calculs r??els, ??taient ??presque une erreur" en comparaison.
Dans les Moyen-Age , l'arithm??tique ??tait l'un des sept arts lib??raux enseign??es dans les universit??s.
L'??panouissement de l'alg??bre dans le m??di??vale islamique monde et dans la Renaissance l'Europe ??tait une excroissance de l'??norme simplification des calcul travers d??cimale notation.
Il existe divers types d'outils pour aider dans les calculs num??riques. Des exemples comprennent r??gles ?? calcul (pour la multiplication, la division et la trigonom??trie) et abaques en plus de la ??lectrique calculateur .
Les op??rations arithm??tiques
Les op??rations arithm??tiques de base sont l'addition, soustraction, multiplication et division, bien que ce sujet comprend ??galement des op??rations plus avanc??es, telles que les manipulations de pourcentages , racines carr??es , exponentiation , et des fonctions logarithmiques . Arithm??tique est effectu??e selon un ordre des op??rations. Tout ensemble d'objets sur lesquels tous les quatre op??rations arithm??tiques (sauf division par z??ro) peut ??tre effectu??e, et o?? ces quatre op??rations ob??issent aux lois habituelles, est appel?? domaine.
Addition (+)
L'addition est le fonctionnement de base de l'arithm??tique. Dans sa forme la plus simple, plus combine deux chiffres, les op??randes ou termes, en un seul chiffre, la somme des nombres.
Ajout de plus de deux nombres peut ??tre consid??r?? comme une addition r??p??t??e; Cette proc??dure est connue en tant que sommation et comprend des moyens d'ajouter une infinit?? de nombres dans un s??rie infinie; addition r??p??t??e du nombre une est la forme la plus ??l??mentaire de compter.
L'addition est commutative et associative donc l'ordre les termes sont ajout??s ?? ne importe pas. Le ??l??ment de l'identit?? de l'addition (la identit?? additive) est 0, ce est-?? 0 ajoutant des rendements en m??me nombre que num??riques. En outre, le ??l??ment inverse de l'addition (la additif inverse) est l'inverse d'un nombre quelconque, ce est, en ajoutant ?? l'oppos?? d'un certain nombre au nombre lui-m??me donne le identit?? additive, 0. Par exemple, ?? l'oppos?? de -7 7 est alors 7 + (-7) = 0 .
L'addition peut ??tre donn??e g??om??triquement comme dans l'exemple suivant:
- Si nous avons deux b??tons de longueurs 2 et 5, si l'on place ensuite les b??tonnets une apr??s l'autre, la longueur de la tige ainsi form??e est 2 + 5 = 7.
Soustraction (-)
La soustraction est ?? l'oppos?? de l'addition. Soustraction trouve la diff??rence entre les deux nombres, le diminuende moins la soustraction. Si le minuende est sup??rieure ?? la soustraction, la diff??rence est positive; si le diminuende est inf??rieure ?? la soustraction, la diff??rence est n??gative; si elles sont ??gales, la diff??rence est ??gale ?? z??ro.
Soustraction ne est ni commutative ni associative. Pour cette raison, il est souvent utile d'examiner la soustraction en tant que l'addition du minuende et ?? l'oppos?? de la soustraction, ce est-a - b = a + (- b). Lorsque ??crite comme une somme, toutes les propri??t??s de plus en attente.
Il existe plusieurs m??thodes de calcul des r??sultats, dont certains sont particuli??rement avantageux de calcul de la machine. Par exemple, les ordinateurs num??riques utilisent la m??thode de le compl??ment ?? deux. D'une grande importance est la m??thode de comptage par lequel le changement est effectu??. Supposons un montant P est donn??e de payer le montant requis Q, avec P sup??rieur ?? Q. Plut??t que d'effectuer la soustraction P - Q et comptant ?? ce montant dans le changement, l'argent est compt?? ?? partir de Q et continue jusqu'?? atteindre P. Bien que le montant compt?? doit ??tre ??gal au r??sultat de la soustraction P - Q, la soustraction n'a jamais vraiment ??t?? fait et la valeur de P - Q peut-??tre encore inconnu du changement-maker.
Multiplication (?? ou ?? ou *)
Multiplication est la deuxi??me op??ration de base de l'arithm??tique. Multiplication combine ??galement deux chiffres dans un num??ro unique, le produit. Les deux num??ros originaux sont appel??s le multiplicateur et le multiplicande, parfois les deux facteurs appel??s simplement.
La multiplication est plus consid??r?? comme une op??ration de mise ?? l'??chelle. Si les num??ros sont imagin??es comme se trouvant dans une ligne, la multiplication par un nombre, par exemple x, sup??rieure ?? 1 est le m??me que tout ??cart qui se ??tend uniform??ment ?? partir de 0, de telle sorte que le nombre 1 lui-m??me est ??tir??e ?? l'endroit o?? x a. De m??me, la multiplication par un nombre inf??rieur ?? 1 peut ??tre imagin?? comme serrant vers 0. (L?? encore, d'une mani??re telle que 1 va ?? l'multiplicande).
La multiplication est commutative et associative; il est en outre distributive sur l'addition et la soustraction. L' identit?? multiplicative est 1, ce est-?? multiplier un nombre quelconque de 1 rendements que m??me num??ro. En outre, le est l'inverse multiplicatif r??ciproque de ne importe quel nombre (sauf z??ro; z??ro est le seul num??ro sans inverse multiplicatif), qui est, en multipliant l'inverse de ne importe quel nombre par le nombre lui-m??me donne le identit?? multiplicatif.
Le produit de a et b est ??crit que a ?? b ou a ??? b. Lorsque a ou b sont des expressions ??crites simplement pas avec les chiffres, il est aussi ??crit par simple juxtaposition: ab. En langages de programmation informatique et de logiciels dans laquelle on ne peut utiliser les caract??res qui se trouvent normalement sur un clavier, il est souvent ??crit avec un ast??risque: a * b.
Division (?? ou /)
La division est essentiellement l'inverse de la multiplication. Division trouve le quotient de deux nombres, le dividende divis?? par le diviseur. Tout dividende divis?? par z??ro ne est pas d??fini. Pour les nombres positifs, si le dividende est plus grand que le diviseur, le quotient est sup??rieur ?? un, sinon ce est moins d'un (une r??gle semblable se applique pour les nombres n??gatifs). Le quotient multipli?? par le diviseur donne toujours le dividende.
Division commutatif ne est ni ni associatif. Comme il est utile d'examiner la soustraction que l'addition, il est utile d'examiner la division que la multiplication des temps de dividendes de la inverse du diviseur, ce est-a ?? b = a ?? 1 / b. Lorsque ??crite en tant que produit, il ob??it ?? toutes les propri??t??s de multiplication.
Arithm??tique d??cimale
Repr??sentation d??cimale se r??f??re exclusivement, d'usage courant, ?? l'??crit syst??me de num??ration utilisant des chiffres arabes que les chiffres pour une radix 10 ("virgule") notation positionnelle; cependant, tout syst??me num??rique bas?? sur des puissances de 10, par exemple, Grecque, Cyrillique, romaine , ou Chinois chiffres peuvent conceptuellement ??tre d??crits comme "notation d??cimale?? ou ??repr??sentation d??cimale".
Les m??thodes modernes pour quatre op??rations fondamentales (addition, soustraction, multiplication et division) ont d'abord ??t?? con??ues par Brahmagupta de l'Inde. Cela a ??t?? connu pendant que l'Europe m??di??vale "Modus Indoram" ou la m??thode des Indiens. Notation de position (aussi connu comme "la notation de valeur de") se r??f??re ?? la repr??sentation et le codage des num??ros utilisant le m??me symbole pour les diff??rents ordres de grandeur (par exemple, la ??ceux place", "des dizaines lieu", "des centaines place??) et, avec un point de base, en utilisant les m??mes symboles pour repr??senter fractions (par exemple, le "lieu dixi??mes", "centi??mes place"). Par exemple, 507,36 d??signe 5 des centaines (10 2), en plus de 0 dizaines (10 1), en plus de 7 unit??s (10 0), en plus de 3/10 (10 -1), plus 6/100 (10) -2.
Z??ro comme un nombre comparable aux autres chiffres de base est un concept qui est essentiel pour cette notation, comme ce est le concept de l'utilisation de z??ro comme un espace r??serv??, et comme ce est la d??finition de la multiplication et addition avec z??ro. L'utilisation de z??ro comme un espace r??serv?? et, par cons??quent, l'utilisation d'une notation de position est d'abord attest?? dans la Texte Jain de l'Inde le droit de la Lokavibh??ga, dat??e 458 AD et ce est seulement au d??but du 13??me si??cle que ces concepts, transmis par l'interm??diaire du bourse d'??tudes du monde arabe, ont ??t?? introduits dans l'Europe par Fibonacci en utilisant le Syst??me de num??ration indo-arabe.
Algorism comprend toutes les r??gles pour effectuer des calculs arithm??tiques en utilisant ce type de chiffre ??crite. Par exemple, l'addition produit la somme de deux nombres arbitraires. Le r??sultat est calcul?? par l'addition r??p??t??e d'un seul chiffre ?? partir de chaque num??ro qui occupe la m??me position, en proc??dant de droite ?? gauche. Une table d'addition avec dix lignes et dix colonnes affiche toutes les valeurs possibles pour chaque somme. Si un individu somme d??passe la valeur neuf, le r??sultat est repr??sent?? avec deux chiffres. Le chiffre le plus ?? droite est la valeur de la position en cours, et le r??sultat de l'addition ult??rieure des chiffres ?? gauche par l'augmentation de la valeur de la seconde (?? gauche) chiffres, ce qui est toujours une. Cet ajustement est appel?? un report de la valeur un.
Proc??d?? pour la multiplication de deux nombres quelconques est similaire au proc??d?? de l'addition. Une table de multiplication par dix lignes et dix colonnes dresse la liste des r??sultats pour chaque paire de chiffres. Si un produit individuel d'une paire de chiffres est sup??rieur ?? neuf, le r??glage de report augmente le r??sultat d'une multiplication ult??rieure de chiffres ?? la gauche d'une valeur ??gale ?? la seconde (?? gauche) chiffre, qui correspond ?? une valeur de un ?? huit (9 ?? 9 = 81). Des ??tapes suppl??mentaires d??finissent le r??sultat final.
Des techniques similaires existent pour la soustraction et la division.
La cr??ation d'un processus adapt?? ?? la multiplication se appuie sur la relation entre les valeurs de chiffres adjacents. La valeur pour chaque chiffre dans un nombre d??pend de sa position. De plus, chaque position ?? gauche repr??sente une valeur dix fois plus grande que la position ?? droite. En termes math??matiques, le repr??sentant de la radix (base) de dix par une augmentation (?? gauche) ou par une diminution (?? droite). Par cons??quent, la valeur de ne importe quel chiffre arbitraire est multipli??e par une valeur de la forme 10 n avec entier n. La liste des valeurs correspondant ?? toutes les positions possibles pour un seul chiffre se ??crit: {..., 10 2, 10, 1, 10 -1, 10 -2, ...}.
Multiplication r??p??t??e de toute valeur dans cette liste de dix produit une autre valeur dans la liste. Dans la terminologie math??matique, cette caract??ristique est d??finie comme fermeture, et la liste pr??c??dente est d??crit comme ferm?? sous la multiplication. Ce est la base pour trouver correctement les r??sultats de multiplication en utilisant la technique pr??c??dente. Ce r??sultat est un exemple de l'utilisation de la th??orie des nombres .
Compos?? unit?? arithm??tique
Compos?? unit?? arithm??tique est l'application d'op??rations arithm??tiques ?? quantit??s de bases multiples tels que pieds et pouces, gallons et les pintes, livres shillings et pence, et ainsi de suite. Avant l'utilisation de syst??mes ?? base de d??cimales-de l'argent et les unit??s de mesure, l'utilisation de l'unit?? de composant arithm??tique form?? une partie importante du commerce et de l'industrie.
Op??rations arithm??tiques de base
Les techniques utilis??es pour l'unit?? de composant arithm??tique a ??t?? d??velopp?? au cours des si??cles et sont bien document??s dans de nombreux manuels dans de nombreuses langues diff??rentes. En plus des fonctions arithm??tiques de base rencontr??es dans l'arithm??tique d??cimale, compos?? unit?? arithm??tique emploie trois autres fonctions:
- R??duction d'une quantit?? de compos?? est r??duit ?? une seule quantit??, par exemple la conversion d'une distance exprim??e en m??tres, pieds et pouces ?? une exprim??e en pouces.
- L'expansion, la fonction inverse ?? la r??duction, est la conversion d'une quantit?? qui est exprim??e comme une seule unit?? de mesure ?? une unit?? de compos??, comme l'??largissement de 24 oz ?? 1, 8 oz
- Normalisation est la conversion d'un ensemble d'unit??s de compos??s ?? un formulaire standard - par exemple la r????criture "1 m 13" que "2 pi 1 po".
La connaissance de la relation entre les diff??rentes unit??s de mesure, leurs multiples et sous-multiples leurs constitue une partie essentielle de l'unit?? de composant arithm??tique.
Principes de l'unit?? de composant arithm??tique
Il ya deux approches de base au compos?? unit?? arithm??tique:
- Proc??d?? de r??duction de la dilatation o?? toutes les variables d'unit?? sont r??duits de compos?? de variables d'unit?? unique, le calcul effectu?? et le r??sultat ??tendu retour ?? des unit??s compos??es. Cette approche adapt??e aux calculs automatis??s. Un exemple typique est le temps de manipulation par Microsoft Excel o?? tous les intervalles de temps sont trait??es comme ?? l'int??rieur des jours et des fractions d??cimales d'un jour.
- En cours m??thode de normalisation dans lequel chaque unit?? est trait??e s??par??ment, et le probl??me est continuellement normalis?? comme la solution se d??veloppe. Cette approche, qui est largement d??crit dans les textes classiques, est le mieux adapt?? pour les calculs manuels. Un exemple de la m??thode de normalisation en cours telle qu'elle est appliqu??e ?? l'addition est repr??sent??e ci-dessous.
| UK pr??-d??cimale monnaie | |||
|---|---|---|---|
|
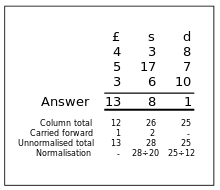
L'op??ration d'addition est effectu??e de droite ?? gauche; dans ce cas, pence sont trait??es en premier, puis suivies par shillings livres. Les num??ros ci-dessous la ??ligne de r??ponse" sont des r??sultats interm??diaires.
Le total de la colonne est pence 25. Comme il ya 12 centimes dans un shilling, le nombre 24 est divis?? par 12 pour donner 2 avec un reste de 1. La valeur "1" est ensuite ??crit ?? la ligne de r??ponse et la valeur " 2 "report?? ?? la colonne de shillings. Cette op??ration est r??p??t??e en utilisant les valeurs de la colonne de shillings, avec l'??tape suppl??mentaire d'ajouter de la valeur qui a ??t?? report?? de la colonne de centimes. Le total interm??diaire est divis?? par 20 plut??t que 12, comme il ya vingt shillings dans une livre. La colonne de la livre est ensuite trait??e, mais comme livres sont la plus grande unit?? qui est envisag??e, aucune valeur sont report??s de la colonne de livres.
Il convient de noter que, par souci de simplicit??, l'exemple choisi ne avait pas deniers.
Op??rations dans la pratique

Au cours des 19e et 20e si??cles diverses aides ont ??t?? ??labor??s pour aider ?? la manipulation des unit??s compos??es, en particulier dans les applications commerciales. Les aides les plus communes ??taient tills m??caniques qui ont ??t?? adapt??s dans des pays comme le Royaume-Uni pour accueillir livres, shillings et pennies liards et "Pr??t Reckoners" - livres visant ?? ce que les commer??ants catalogu??s les r??sultats de divers calculs de routine telles que les pourcentages ou multiples de diverses sommes d'argent. Un livret typique qui a couru 150 pages sous forme de tableaux multiples "une ?? dix mille dans les diff??rents prix d'un centime ?? une livre".
La lourdeur de l'unit?? de composant arithm??tique a ??t?? reconnu depuis de nombreuses ann??es - en 1586, le math??maticien flamand Simon Stevin publi?? une petite brochure intitul??e De thiende ("le dixi??me") dans lequel il a d??clar?? que l'introduction universelle de d??cimales pi??ces de monnaie, des mesures et des poids pour ??tre simplement une question de temps alors que dans l'??re moderne, de nombreux programmes de conversion, comme que noy?? dans la calculatrice fournie en standard des sept exploitation des unit??s compos??es d'affichage du syst??me de Microsoft Windows dans un format d??cimal r??duite plut??t que d'utiliser un format ??largi (ie "2,5 m" se affiche plut??t que "2 pi 6 po").
La th??orie des nombres
Le terme se r??f??re ??galement ?? l'arithm??tique la th??orie des nombres. Cela comprend les propri??t??s des nombres entiers li??s ?? la primalit?? , la divisibilit?? et le solution des ??quations dans entiers, ainsi que la recherche moderne qui est une excroissance de cette ??tude. Ce est dans ce contexte que l'on traverse le th??or??me fondamental de l'arithm??tique et de fonctions arithm??tiques. Un Cours en arithm??tique par Jean-Pierre Serre refl??te cet usage, comme le font ces phrases comme premier ordre arithm??tique ou la g??om??trie alg??brique arithm??tique. La th??orie des nombres est ??galement d??sign?? sous le nom arithm??tique ult??rieure, comme dans le titre de Le livre de Harold Davenport sur le sujet.
Arithm??tique dans l'??ducation
L'enseignement primaire en math??matiques met souvent l'accent sur des algorithmes pour l'arithm??tique des nombres naturels , entiers , fractions et d??cimales (en utilisant le syst??me de valeur de d??cimales). Cette ??tude est parfois connu comme algorism.
La difficult?? et l'apparence d??motiv??s de ces algorithmes a longtemps conduit les ??ducateurs ?? se interroger sur ce programme, pr??conisant l'enseignement pr??coce des id??es math??matiques plus centrales et intuitives. Un mouvement notable dans cette direction a ??t?? la New Math des ann??es 1960 et 1970, qui a tent?? d'enseigner l'arithm??tique dans l'esprit du d??veloppement axiomatique de la th??orie des ensembles, un ??cho de la tendance qui pr??vaut dans les math??matiques sup??rieures.
