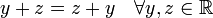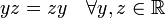Commutativit??

Exemple montrant la commutativit?? de l'addition (3 + 2 = 2 + 3)

Commutativit?? est largement utilis?? math??matique terme qui renvoie ?? la capacit?? de changer l'ordre de quelque chose sans changer le r??sultat final. Ce est une propri??t?? fondamentale dans la plupart des branches des math??matiques et de nombreuses preuves en d??pendent. La commutativit?? des op??rations simples ??tait depuis de nombreuses ann??es et suppose implicitement la propri??t?? n'a pas ??t?? donn?? un nom ou attribu??s jusqu'au 19e si??cle, lorsque les math??maticiens ont commenc?? ?? formaliser la th??orie des math??matiques.

Les utilisations courantes

La propri??t?? commutative (ou loi commutative) est une propri??t?? associ??e ?? op??rations binaires et fonctions . De m??me, si la propri??t?? commutative est valable pour une paire d'??l??ments sous une certaine op??ration binaire alors il est dit que les deux ??l??ments font la navette dans cette op??ration.

En groupe et la th??orie des ensembles , de nombreuses structures alg??briques sont appel??s commutative lorsque certains op??randes satisfont la propri??t?? commutative. En plus hautes branches des math??matiques, comme l'analyse et alg??bre lin??aire la commutativit?? des op??rations bien connues (comme plus et la multiplication des nombres r??els et complexes) est souvent utilis?? (ou implicitement suppos??) dans les preuves.

D??finitions math??matiques

Le terme ??commutative?? est utilis?? dans plusieurs sens connexes.

1. op??ration binaire * sur un ensemble S est dit commutatif si:

x * y = y * x pour tout x, y ∈ S

• Une op??ration qui ne satisfait pas la propri??t?? ci-dessus est appel?? non commutative.

2. On dit que x commute avec Y sous * si:

x * y = y * x

3. Un fonction binaire f: A ?? A → B est dit commutatif si:

f (x, y) = f (y, x) pour tout x, y ∈ A.

Histoire et ??tymologie

La premi??re utilisation connue du terme ??tait dans un Journal fran??ais publi?? en 1814

Dossiers de l'utilisation implicite de la propri??t?? commutative remontent ?? l'Antiquit??. Les Egyptiens utilisaient la commutativit?? de la multiplication de simplifier l'informatique produits. Euclid est connu pour avoir assum?? la propri??t?? commutative de la multiplication dans son livre Elements . Utilisations formelles de la propri??t?? commutative surgi ?? la fin du 18e et d??but du 19e si??cle, lorsque les math??maticiens ont commenc?? ?? travailler sur une th??orie des fonctions. Aujourd'hui la propri??t?? commutative est une propri??t?? bien connue et de base utilis?? dans la plupart des branches des math??matiques. Les versions simples de la propri??t?? commutative sont g??n??ralement enseign??es dans commen??ant cours de math??matiques.

La premi??re utilisation du terme commutative r??elle ??tait dans un m??moire par Fran??ois Servois en 1814, qui a utilis?? le mot commutatives pour d??crire les fonctions qui ont ce qu'on appelle maintenant la propri??t?? commutative. Le mot est une combinaison du mot fran??ais qui signifie de banlieue "de remplacer ou de switch" et le suffixe sens -ative "tendant ??" de sorte que le mot signifie litt??ralement ??tendant ?? substituer ou commutateur." Le terme est alors apparu en anglais Philosophical Transactions de la Royal Society en 1844.

Propri??t??s connexes

Graphique montrant la sym??trie de la fonction d'addition

Associativit??

La propri??t?? associative est ??troitement li??e ?? la propri??t?? commutative. La propri??t?? associative indique que l'ordre dans lequel les op??rations sont effectu??es ne affecte pas le r??sultat final. En revanche, la propri??t?? commutative indique que l'ordre des termes ne affecte pas le r??sultat final.

Sym??trie

Sym??trie peut ??tre directement li??e ?? la commutativit??. Quand un op??rateur commutatif est ??crit comme une fonction binaire alors la fonction r??sultante est sym??trique ?? travers la ligne y = x. Par exemple, si nous laissons une fonction f repr??sentent plus (une op??ration commutative), de sorte que f (x, y) = x + y alors f est une fonction sym??trique qui peut ??tre vu dans l'image sur la droite.

Exemples

Op??rations commutatives dans la vie quotidienne

• Mettre vos chaussures ressemble ?? une op??ration commutative, car il n'a pas d'importance si vous mettez la chaussure gauche ou ?? droite sur la premi??re, le r??sultat final (ayant deux chaussures), est le m??me.
• Lors de changement que nous profitons de la commutativit?? de l'addition. Il ne importe pas quel ordre nous mettons le changement, il ajoute toujours le m??me total.

Op??rations commutatives en math??matiques

Exemple montrant la commutativit?? de la multiplication (3 * 5 = 5 * 3)

Deux exemples bien connus des op??rations binaires sont commutatives:

• Le plus des nombres r??els , qui est commutative depuis

Par exemple 4 + 5 + 4 = 5, car les deux 9 expressions sont ??gales.

• La multiplication des nombres r??els , qui est commutative depuis

Par exemple, 3 x 5 = 5 ?? 3, ??tant donn?? que 15 les deux expressions ??gaux.

• D'autres exemples d'op??rations binaires commutatives comprennent l'addition et la multiplication des nombres complexes , outre des vecteurs , et intersection et union de ensembles.

Op??rations non commutatives dans la vie quotidienne

Concat??nation, l'acte de se joindre ?? des cha??nes de caract??res ensemble, est une op??ration non commutative.

• Laver et s??cher vos v??tements ressemble ?? une op??ration non commutative, si vous s??che d'abord, puis lavez, vous obtenez un r??sultat significativement diff??rente que si vous vous lavez d'abord, puis sec.
• Le Cube de Rubik est non commutative. Par exemple, tordant le visage vers la droite avant, la face sup??rieure dans le sens horaire et la face avant dans le sens antihoraire (FUF) n'a pas donn?? le m??me r??sultat que la torsion de la face avant dans le sens horaire, puis la gauche et enfin tourner dans le sens horaire sup??rieure (FF'U). Les rebondissements ne commutent pas. Ce est ??tudi?? dans la th??orie des groupes .

Op??rations non commutatives en math??matiques

Certaines op??rations binaires non commutatives sont:

• la soustraction est non commutative depuis
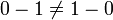
• division est non commutative depuis
• matrice multiplication est non commutative depuis

Structures et commutativit?? math??matiques

• Une groupe ab??lien est un groupe dont le fonctionnement groupe est commutatif.
• Un anneau commutatif est un anneau dont la multiplication est commutative. (Addition dans un anneau est par d??finition toujours commutative.)
• Dans un domaine tant addition et la multiplication sont commutative.
• Le centre est le plus grand sous-ensemble d'un groupe commutatif.