La preuve math??matique

En math??matiques , une preuve est une d??monstration convaincante que certains ??nonc?? math??matique est n??cessairement vrai, dans les normes reconnues du champ. Une preuve est une logique argumentation, pas une une empirique. Ce est, la preuve doit d??montrer qu'une proposition est vraie dans tous les cas auxquels elle se applique, sans une seule exception. Une proposition non prouv??e croyait ou fortement soup??onn??e d'??tre vrai est connu comme un conjecture.

Preuves emploient logique mais incluent habituellement une certaine quantit?? de langage naturel qui admet g??n??ralement une certaine ambigu??t??. En fait, la grande majorit?? des preuves ??crites en math??matiques peut ??tre consid??r?? comme des applications de la logique informelle. Purement preuves formelles sont pris en compte dans th??orie de la preuve. La distinction entre preuves formelles et informelles a conduit ?? beaucoup de Examen de courant et historique pratique math??matique, quasi-empirisme en math??matiques, et soi-disant math??matiques folkloriques (dans les deux de sens de ce terme). Le philosophie des math??matiques est pr??occup?? par le r??le du langage et de la logique dans les preuves, et les math??matiques comme un langage.

Ind??pendamment de l'attitude de l'un au formalisme, le r??sultat qui est prouv?? pour ??tre vrai est un th??or??me ; dans une preuve compl??tement formelle, il serait la derni??re ligne, et la preuve compl??te montre comment il r??sulte de la axiomes seule par l'application des r??gles d'inf??rence. Une fois qu'un th??or??me est d??montr??, il peut ??tre utilis?? comme base pour prouver d'autres ??tats. Un th??or??me peut ??galement ??tre consid??r?? comme un lemme se il est utilis?? comme un tremplin dans la d??monstration d'un th??or??me. Les axiomes sont ces d??clarations on ne peut pas, ou ne ont pas, prouver. Ce sont une fois l'??tude principale des philosophes des math??matiques. Aujourd'hui l'accent est mis davantage sur la pratique, ce est ?? dire des techniques acceptables.

Modes de preuve

Preuve directe

En preuve directe, la conclusion est ??tabli par la combinaison logique des axiomes, d??finitions et th??or??mes pr??c??dents. Par exemple, la preuve directe peut ??tre utilis?? pour ??tablir que la somme de deux m??me entiers est toujours m??me:

Pour toute deux entiers pairs et 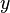nous pouvons ??crire 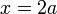et 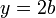pour certains entiers et 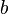Puisque les deux et 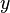sont des multiples de 2. Mais la somme 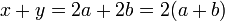est aussi un multiple de deux, de sorte qu'il est donc, par d??finition m??me.

Cette preuve utilise d??finition des entiers pairs, ainsi que droit de la distribution.

Preuve par induction

En preuve par induction, d'abord un "sc??nario de base" est prouv??, puis une ??r??gle d'induction?? est utilis?? pour prouver un (souvent infini) s??rie d'autres cas. Depuis le cas de base est vrai, l'infinit?? d'autres cas doit aussi ??tre vrai, m??me si chacun d'eux ne peut ??tre prouv??e directement en raison de leur nombre infini. Un sous-ensemble de l'induction est Descente infinie. Infini descente peut ??tre utilis?? pour prouver la irrationalit?? de la racine carr??e de deux.

Le principe de l'induction math??matique pr??cise que: Soit N = {1, 2, 3, 4, ...} l'ensemble des nombres naturels et P (n) un ??nonc?? math??matique impliquant le nombre naturel n appartenant ?? N tel que ( i) P (1) est vrai, ce est-P (n) est vraie pour n = 1 (ii) P (m + 1) est vrai chaque fois que P (m) est vrai, ce est-P (m) est vrai implique que P (m + 1) est vrai. Alors P (n) est vrai pour l'ensemble des nombres naturels N.

Preuve par transposition

Preuve par Transposition ??tablit la conclusion ??si p, alors q" en prouvant l'??quivalent d??claration contrapositive "si ce ne est donc pas q p".

Preuve par l'absurde

Dans la preuve par l'absurde (??galement connu sous le nom reductio ad absurdum, latin pour "la r??duction dans l'absurde"), il est d??montr?? que si certaines d??clarations ??taient fausses, une contradiction logique se produit, d'o?? la d??claration doit ??tre vrai. Cette m??thode est peut-??tre la plus r??pandue des preuves math??matiques. Un exemple c??l??bre d'une preuve par l'absurde montre que 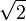est irrationnelle :

Supposer que 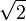est rationnel, donc 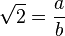o?? a et b sont des nombres entiers non nuls sans facteur commun (d??finition du nombre rationnel). Ainsi, 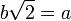. Quadrature deux c??t??s donne 2 b ² = ^2. Depuis 2 divise le c??t?? gauche, 2 doivent ??galement diviser le c??t?? droit (comme elles sont ??gales et les deux nombres entiers). Ainsi, un ^deux est encore, ce qui implique que A doit ??tre aussi m??me. On peut donc ??crire a = c 2, o?? c est un entier ??galement. Remplacement dans les rendements d'origine de l'??quation 2 b = ² (2 c) ² = 4 c ^2. Divisant les deux c??t??s par deux rendements b = ² 2 ² c. Mais alors, par le m??me argument comme avant, 2 divise b ^2, donc b doit ??tre encore. Toutefois, si A et B sont ?? la fois m??me, ils partagent un facteur, ?? savoir 2. Cela contredit notre hypoth??se, si nous sommes oblig??s de conclure que 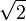est irrationnel.

La preuve par la construction

La preuve par la construction, ou la preuve par l'exemple, est la construction d'un exemple concret avec une propri??t?? de montrer que quelque chose ayant cette propri??t?? existe. Joseph Liouville, par exemple, a prouv?? l'existence de nombres transcendants par la construction d'un exemple explicite.

Preuve par l'??puisement

Dans Preuve par l'??puisement, la conclusion est ??tablie en la divisant en un nombre fini de cas et de prouver chacun s??par??ment. Le nombre de cas peut parfois devenir tr??s volumineux. Par exemple, la premi??re preuve de la th??or??me des quatre couleurs ??tait une preuve par l'??puisement avec 1936 cas. Cette preuve a ??t?? controvers??e parce que la majorit?? des cas ont ??t?? v??rifi??s par un programme d'ordinateur, pas ?? la main. La preuve la plus courte connue du th??or??me des quatre couleurs aujourd'hui a encore plus de 600 cas.

Preuve probabiliste

Une preuve probabiliste est celui dans lequel est repr??sent?? un exemple d'exister, avec certitude, en utilisant les m??thodes de la th??orie des probabilit??s . Ce ne est pas ??tre confondu avec un argument qui est un th??or??me ??probablement?? vrai. Le dernier type de raisonnement peut ??tre appel?? un ??argument de la plausibilit???? et ne est pas une preuve; dans le cas de la Collatz Conjecture il est clair dans quelle mesure ce est d'une v??ritable preuve. Preuve probabiliste, comme la preuve par construction, est l'une des nombreuses fa??ons de montrer th??or??mes d'existence.

Preuve combinatoire

Une preuve combinatoire ??tablit l'??quivalence des expressions diff??rentes en montrant qu'ils comptent le m??me objet de diff??rentes mani??res. Habituellement, un bijection est utilis?? pour montrer que les deux interpr??tations donnent le m??me r??sultat.

La preuve nonconstructive

Une preuve nonconstructive ??tablit qu'un certain objet math??matique doit exister (par exemple ??Certains X satisfait f (X)"), sans expliquer comment un tel objet peut ??tre trouv??. Souvent, cela prend la forme d'une d??monstration par l'absurde dans laquelle la non-existence de l'objet se av??re ??tre impossible. En revanche, une preuve constructive ??tablit qu'un objet particulier existe en fournissant un proc??d?? de le trouver. Un exemple c??l??bre d'une preuve nonconstructive montre qu'il existe deux nombres irrationnels et 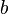tel que 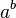est un nombre rationnel :

Non plus 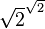est un nombre rationnel et nous fait (prendre 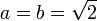), Ou 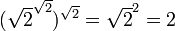montre que nous pouvons prendre 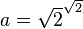et .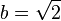

Preuve ni r??futation

Il ya une classe d'??nonc??s math??matiques pour lesquels ni une preuve ni r??futation existe, en utilisant seulement ZFC, la forme standard de la th??orie des ensembles axiomatique . Des exemples comprennent le hypoth??se continuum; voir plus loin Liste des d??clarations ind??cidable dans ZFC. Sous l'hypoth??se que ZFC est coh??rente, l'existence de ces ??tats r??sulte de (Premier) th??or??me d'incompl??tude de G??del. Si une proposition non prouv??e particulier peut ??tre prouv??e ou r??fut??e utilise un ensemble standard d'axiomes ne est pas toujours ??vident, et peut ??tre extr??mement technique pour d??terminer. Pour montrer qu'un ??nonc?? math??matique est ind??pendant (ou ind??cidable) dans une formalisation donn?? de math??matiques tels que ZFC exige des m??thodes qui transcendent la formalisation donn??.

Preuve ??l??mentaire

Une preuve ??l??mentaire est (habituellement) une preuve qui ne utilise pas l'analyse complexe. Depuis quelque temps, on a pens?? que certains th??or??mes, comme le th??or??me des nombres premiers, ne pouvait ??tre prouv?? en utilisant les math??matiques ??sup??rieures??. Cependant, au fil du temps, beaucoup de ces r??sultats ont ??t?? r??primand?? en utilisant des techniques ??l??mentaires seulement.

Fin d'une preuve

Parfois, l'abr??viation "CQFD" est ??crit pour indiquer la fin d'une preuve. Cette abr??viation de ??Quod Erat DEMONSTRANDUM", qui est latine pour "ce qui devait ??tre d??montr??". Une alternative consiste ?? utiliser un carr?? ou un rectangle, par exemple ∎ □ ou, connu comme un " pierre tombale ??ou?? Halmos ".