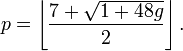Th??or??me des quatre couleurs

Exemple d'une carte ?? quatre couleurs

Le th??or??me des quatre couleurs (aussi connu comme la carte th??or??me des quatre couleurs) indique que, compte tenu tout plan s??par?? en r??gions, comme une carte politique des Etats d'un pays, les r??gions peuvent ??tre color??s en utilisant pas plus de quatre couleurs de mani??re que deux r??gions adjacentes re??oivent la m??me couleur. Deux r??gions sont appel??es ?? c??t?? que se ils partagent un segment de la fronti??re, et pas seulement un point. Chaque r??gion doit ??tre contigu: autrement dit, il peut ne pas ??tre enclaves comme certains pays r??els tels que l'Angola , l'Azerba??djan , l' ??tats-Unis ou la Russie .

Ce est souvent le cas que l'utilisation de seulement trois couleurs est insuffisante. Cela se applique d??j?? ?? la carte avec une r??gion entour??e par trois autres r??gions (mais avec un nombre pair de pays environnants trois couleurs sont assez) et il ne est pas du tout difficile de prouver que cinq couleurs suffisent pour colorier une carte.

Le th??or??me des quatre couleurs ??tait le premier grand th??or??me ?? d??montrer l'utilisation d'un ordinateur, et la preuve ne est pas accept??e par tous les math??maticiens, car il serait impossible pour un humain de v??rifier ?? la main (voir la preuve assist??e par ordinateur). En fin de compte, pour croire la preuve, il faut avoir la foi en la justesse de la compilateur et l'ex??cution du programme mat??riel utilis?? pour l'??preuve.

Le manque d'??l??gance math??matique par la communaut?? math??matique g??n??rale ??tait un autre facteur, et pour paraphraser les commentaires de l'??poque, "une bonne preuve math??matique est comme un po??me-ce est un r??pertoire t??l??phonique! "

Histoire

Le conjecture a ??t?? propos??e pour la premi??re en 1852 lorsque Francis Guthrie, tout en essayant de colorer la carte de comt??s de l'Angleterre , a remarqu?? que seulement quatre couleurs diff??rentes ont ??t?? n??cessaires. ?? l'??poque, le fr??re de Guthrie, Fredrick, ??tait un ??tudiant de Auguste De Morgan au University College. Francis demanda avec Fredrick son sujet, qui a ensuite pris ?? De Morgan. (Fredrick Guthrie a obtenu plus tard en 1852, et plus tard est devenu un professeur de math??matiques en Afrique du Sud ). Selon De Morgan:

Un de mes ??tudiants [Guthrie] m'a demand?? aujourd'hui de lui donner une raison ?? un fait que je ne savais pas, ce est un fait - et ne avez pas encore. Il dit que si un chiffre est en tout cas divis?? et les compartiments de couleurs diff??rentes de sorte que les chiffres avec une partie de la ligne de fronti??re commune sont de couleurs diff??rentes - quatre couleurs peuvent ??tre voulu, mais pas plus-qui suit est le cas dans lequel quatre couleurs sont recherch??s. Requ??te ne peut pas une n??cessit?? pour cinq ou plus ??tre invent?? ...

La premi??re r??f??rence est publi?? par Arthur Cayley, qui cr??dite ensuite la conjecture de De Morgan.

Il ya eu plusieurs tentatives infructueuses de d??but prouver le th??or??me . Une preuve du th??or??me a ??t?? donn??e par Alfred Kempe en 1879, qui a ??t?? largement acclam??; une autre preuve a ??t?? donn??e par Peter Guthrie Tait en 1880. Ce ne est qu'en 1890 que la preuve de Kempe a ??t?? montr?? par incorrecte Percy Heawood et 1891 que la preuve de Tait a ??t?? montr?? par incorrecte Julius Petersen-chaque fausse preuve ne ??tait pas contest??e pendant 11 ans.

En 1890, en plus d'exposer la faille dans la preuve de Kempe, Heawood prouv?? que tous les graphes planaires sont cinq coloriable; voir cinq th??or??me de couleur.

Des r??sultats significatifs ont ??t?? r??alis??s par la Croatie math??maticien Danilo Blanusa dans les ann??es 1940 en trouvant un original snark.

Pendant les ann??es 1960 et 1970 en allemand math??maticien Heinrich Heesch a d??velopp?? des m??thodes d'application de la ordinateur ?? la recherche de la preuve.

Ce ne est qu'en 1976 que la conjecture quatre couleurs a finalement ??t?? prouv?? par Kenneth Appel et Wolfgang Haken au Universit?? de l'Illinois. Ils ??taient assist??s dans certains travaux par algorithmique John Koch.

Si la conjecture de quatre couleurs ??taient fausses, il y aurait au moins une carte avec le plus petit nombre possible de r??gions qui n??cessite cinq couleurs. La preuve a montr?? qu'une telle contre-exemple minimal ne peut exister par l'utilisation de deux concepts techniques:

• Un jeu incontournable contient des r??gions telles que chaque carte doit avoir au moins une r??gion de cette collection.
• Une configuration r??ductible est un arrangement de pays qui ne peuvent pas se produire dans un contre-minime. Si une carte contient une configuration r??ductible, et le reste de la carte peut ??tre color?? avec quatre couleurs, la carte enti??re peut ??tre color?? avec quatre couleurs et ainsi de cette carte ne est pas minime.

Utilisation des r??gles et des proc??dures math??matiques bas??s sur les propri??t??s des configurations r??ductibles (par exemple, le m??thode de d??charge, bagues, cha??nes Kempe, etc.), Appel et Haken trouv?? un ensemble in??vitable de configurations r??ductibles, prouvant ainsi que un contre minimal pour la conjecture quatre couleurs ne pourrait pas exister. Leur d??monstration r??duit l'infinit?? de cartes possibles pour 1936 configurations r??ductibles (plus tard r??duite ?? 1476) qui devait ??tre v??rifi?? un par un par ordinateur. Cette partie de r??ductibilit?? du travail a ??t?? ind??pendamment une double v??rification avec diff??rents programmes et les ordinateurs. Cependant, la partie in??vitabilit?? de la preuve ??tait plus de 500 pages manuscrites de contre-contre-exemples, dont une grande partie ??tait fils adolescent de Haken Lippold v??rifier colorations de graphes. Le programme informatique a couru pour des centaines d'heures.

Depuis le proving du th??or??me, des algorithmes efficaces ont ??t?? trouv??s pour les cartes 4-colorants n??cessitant seulement O (n ²⁾ fois, o?? n est le nombre de sommets. En 1996 , Neil Robertson, Daniel P. Sanders, Paul Seymour, Thomas et Robin cr???? un algorithme quadratique du temps, en utilisant Le travail d'Edward Belaga pour am??liorer un algorithme quartique sur la base de la preuve de Appel et Haken. Cette nouvelle preuve est similaire ?? Appel et Haken de mais plus efficace car il r??duit la complexit?? du probl??me et doit v??rifier seulement 633 configurations r??ductibles. Les deux parties in??luctable et r??ductibilit?? de cette nouvelle preuve doivent ??tre ex??cut??es par ordinateur et ne sont pas pratiques pour v??rifier ?? la main.

En 1980, George Spencer-Brown a d??pos?? sa preuve suppos??e de la carte th??or??me des quatre couleurs ?? la Royal Society. La validit?? de cette preuve, qui constitue l'annexe 5 de la traduction allemande de son livre " Lois du formulaire "(L??beck 1997), est g??n??ralement mis en doute.

En 2004 Benjamin Werner et Georges Gonthier a formalis?? une preuve du th??or??me ?? l'int??rieur du Assistant de preuves Coq (Gonthier, sd). Cela supprime la n??cessit?? de faire confiance aux divers programmes informatiques utilis??s pour v??rifier des cas particuliers; il est seulement n??cessaire de faire confiance au noyau Coq.

Il ya aussi des algorithmes efficaces pour d??terminer si une ou deux couleurs suffisent pour colorier une carte. D??terminer si trois couleurs suffisent est, cependant, NP-complet, et donc un algorithme rapide est peu probable. D??terminer si un g??n??ral (??ventuellement non plane) graphique peut ??tre quatre-couleur est ??galement NP-complet.

Pas pour les cartographes

Bien que le th??or??me des quatre couleurs a ??t?? d??couvert dans le processus de coloration d'une vraie carte, il est rarement utilis?? en pratique cartographie. Selon Kenneth mai, un historien math??matique qui a ??tudi?? un ??chantillon d'atlas ?? la Biblioth??que du Congr??s, il n'y a pas tendance ?? minimiser le nombre de couleurs utilis??es. Beaucoup de cartes utilisent la couleur pour des choses autres que les r??gions politiques. La plupart des cartes utilisent plus de quatre couleurs, et quand seulement quatre couleurs sont utilis??es, g??n??ralement le nombre minimum de couleurs effectivement n??cessaires est inf??rieur ?? quatre.

Sur la plupart des cartes r??elles il ya des lacs, qui doivent tous ??tre de la m??me couleur. Ce est alors suppl??mentaire pour les couleurs qui sont obligatoires pour les r??gions politiques. Si les lacs sont compt??s comme une seule r??gion, le th??or??me ne se applique pas. Il peut ??tre appliqu?? aux zones terrestres du carte seule en consid??rant les lacs que ne appartenant pas ?? la carte des r??gions, mais sur des cartes r??elles de plusieurs non- r??gions de carte contigus peuvent en outre appartenir ?? une seule non- connect?? r??gion politique et exigent la m??me couleur (voir ci-dessous ), alors l?? encore le th??or??me ne se applique pas.

Manuels sur la cartographie et de la histoire de la cartographie ne mentionnent pas le th??or??me des quatre couleurs, m??me si coloration de la carte est un sujet de discussion. G??n??ralement, les cartographes disent qu'ils sont plus pr??occup??s par la coloration cartes politiques de fa??on ??quilibr??e, de sorte qu'aucune couleur unique domine. Qu'ils utilisent quatre, cinq ou plus de couleurs ne est pas une pr??occupation majeure.

D??claration officielle en th??orie des graphes

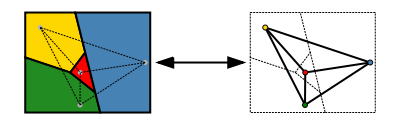
Pour indiquer formellement le th??or??me, il est plus facile de reformuler dans la th??orie des graphes. Il d??clare ensuite que le sommets de chaque graphe planaire peut ??tre color?? avec au plus quatre couleurs de sorte que deux sommets adjacents re??oivent la m??me couleur. Ou "tout graphe planaire est quatre coloriable" pour faire court. Ici, chaque r??gion de la carte est remplac?? par un sommet du graphe, et deux sommets sont reli??s par une bord si et seulement si les deux r??gions partagent un segment de bordure (pas seulement un coin).

Faux r??futations

Comme beaucoup de c??l??bres probl??mes ouverts de math??matiques, le th??or??me des quatre couleurs a attir?? un grand nombre de fausses preuves et r??futations de sa longue histoire. Certains, comme Kempe et de Tait mentionn?? ci-dessus, se tenait ?? l'examen public pendant plus d'une d??cennie avant ils ont ??t?? expos??s. Mais beaucoup d'autres, r??dig?? par des amateurs, ne ont jamais ??t?? publi??s du tout.

Cette carte a ??t?? color?? avec cinq couleurs ...	... Mais il est n??cessaire de modifier au moins quatre des dix r??gions pour obtenir une coloration avec seulement quatre couleurs.

G??n??ralement, la tentative la plus simple "des contre-?? pour cr??er une r??gion qui touche toutes les autres r??gions. Cela force les autres r??gions ?? colorer avec seulement trois couleurs. Parce que le th??or??me des quatre couleurs est vrai, ce est toujours possible; Cependant, parce que la personne dessiner la carte est ax??e sur une vaste r??gion, ils ne ont pas remarqu?? que les autres r??gions peuvent en effet ??tre color??s avec trois couleurs.

Cette astuce peut ??tre g??n??ralis??e: il ya beaucoup de cartes o??, si les couleurs de certaines r??gions sont s??lectionn??s ?? l'avance, il devient impossible de colorier les r??gions restantes sans d??passer quatre couleurs. Un v??rificateur occasionnel de la contre-ne peut pas penser ?? changer les couleurs de ces r??gions, de sorte que le contre appara??t comme si elle est valide.

Peut-??tre un effet de base de cette id??e fausse commune est le fait que la restriction de couleur ne est pas transitive: une r??gion ne doit ??tre color??e diff??remment r??gions, il touche directement, et non les r??gions touchant les r??gions qu'il touche. Si ce ??tait la restriction, graphes planaires exigeraient arbitrairement un grand nombre de couleurs.

Autres fausses r??futations violent les hypoth??ses du th??or??me de mani??re inattendue, comme l'utilisation d'une r??gion qui se compose de plusieurs parties d??connect??es, ou en interdisant les r??gions de la m??me couleur de toucher ?? un point.

G??n??ralisations

En rejoignant les fl??ches simples ensemble et les doubles fl??ches ensemble, on obtient un tore avec sept r??gions mutuellement touchantes; donc sept couleurs sont n??cessaires

Cette construction montre les tore divis?? par le maximum de sept r??gions, dont chacune touche tous les autres.

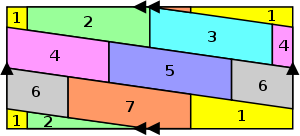
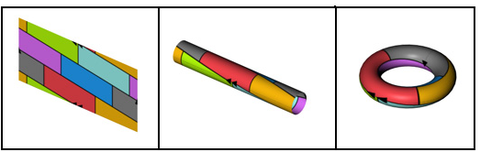
On peut aussi consid??rer le probl??me de coloration sur des surfaces autres que le plan . Le probl??me sur la sph??re ou cylindre est ??quivalente ?? celle de l'avion. Pour ferm??e (orientable ou non orientable) surfaces avec positif genre, le nombre maximum de p couleurs n??cessaires d??pend de la surface caract??ristique d'Euler χ selon la formule

,

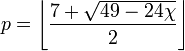o?? les parenth??ses indiquent le plus ?? l'ext??rieur fonction de-chauss??e. La seule exception ?? la formule est la bouteille de Klein , qui a caract??ristique d'Euler 0 et n??cessite 6 couleurs. Ce ??tait initialement connu sous le nom Conjecture Heawood et prouv?? que La Carte Couleur th??or??me par Gerhard Ringel et JTW Youngs en 1968.

Alternativement, pour un surface orientable la formule peut ??tre donn??e en termes de genre d'une surface, g:

Par exemple, le tore poss??de Euler caract??ristique χ = 0 (et genre g = 1), et donc p = 7, de sorte que pas plus de sept couleurs sont n??cessaires pour colorer ne importe quelle carte sur un tore.

Un Ruban de M??bius exige ??galement six couleurs.

Il n'y a pas d'extension utile du probl??me de coloration des r??gions solides tridimensionnels. Il est trivial de construire un ensemble de n tiges flexibles, par exemple, de telle sorte que chaque tige touche chaque autre tige. L'ensemble n??cessiterait alors n couleurs ou n + 1 si vous consid??rez l'espace vide qui touche ??galement tous les tige. n peut ??tre consid??r?? comme un nombre entier quelconque, aussi grande que souhait??e.

Les r??gions non-contigu??s

Exemple d'une carte avec des r??gions non-contigu??s

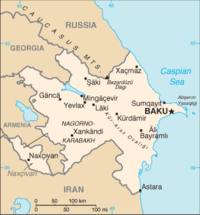
Dans le monde r??el, tous les pays ne sont contigus (par exemple, Alaska dans le cadre de la Etats-Unis , Nakhitchevan dans le cadre de l'Azerba??djan , et Kaliningrad dans le cadre de la Russie ). Si le sch??ma de couleurs choisie exige que le territoire d'un pays donn?? doit ??tre de la m??me couleur, quatre couleurs peuvent ne pas ??tre suffisant. Par exemple, consid??rons une carte simplifi??e:

Dans cette carte, les deux r??gions ??tiquet??es A appartiennent au m??me pays, et doit ??tre de la m??me couleur. Cette carte n??cessite alors cinq couleurs, ??tant donn?? que les deux r??gions sont contigu??s A, conjointement avec quatre autres r??gions, dont chacun est contigu ?? toutes les autres. Si A est compos??e de trois r??gions, six couleurs ou plus pourrait ??tre n??cessaire; on peut construire des cartes qui n??cessitent un nombre arbitrairement ??lev?? de couleurs.