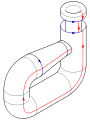
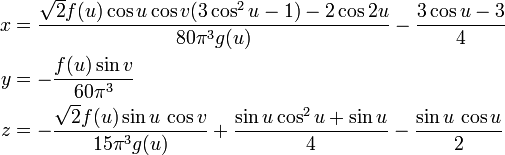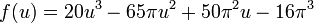La bouteille de Klein
Renseignements g??n??raux
Enfants SOS offrent un chargement complet de la s??lection pour les ??coles pour une utilisation sur les intranets des ??coles. Tous les enfants disponibles pour le parrainage de SOS Enfants des enfants sont pris en charge dans une maison de famille pr??s de la charit??. Lire la suite ...

En math??matiques , la bouteille de Klein est un certain non- orientable surface, ce est ?? dire, une surface (une ?? deux dimensions espace topologique) sans c??t??s distincts et ??internes?? ??ext??rieur??. Autres objets non orientables connexes comprennent la Ruban de M??bius et la plan projectif r??el. Tandis qu'un ruban de M??bius est un objet ?? deux dimensions avec un c??t?? et un bord, une bouteille de Klein est un objet tridimensionnel avec un c??t?? et sans ar??tes. (A titre de comparaison, une sph??re est un objet tridimensionnel sans ar??tes et deux c??t??s).
La bouteille de Klein a ??t?? d??crite en 1882 par l' allemand math??maticien Felix Klein. Il a ??t?? initialement nomm?? la ??surface Klein" Kleinsche Fl??che; Cependant, cela a ??t?? mal interpr??t?? comme Kleinsche Flasche "bouteille de Klein", qui a finalement conduit ?? l'adoption de ce terme dans la langue allemande ainsi.
Construction
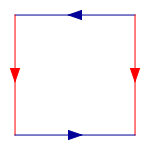
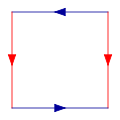
Commencez avec un carr??, puis coller ensemble les bords de couleur correspondant, dans le diagramme suivant, de sorte que les fl??ches correspondance. Plus formellement, la bouteille de Klein est le espace quotient d??crit comme le carr?? [0,1] ?? [0,1] dont les c??t??s sont d??finis par les relations (0, y) ~ (1, y) pour 0 ≤ y ≤ 1 et (x, 0) ~ (1 - x, 1) pour 0 ≤ x ≤ 1:
Cette place est un polygone fondamental de la bouteille de Klein.
Notez que ce est un "abstrait" collage en ce sens que d'essayer de r??aliser ce r??sultat en trois dimensions en une bouteille de Klein auto-intersection. La bouteille de Klein, bon, ne pas se entrecroiser. N??anmoins, il est un moyen de visualiser la bouteille de Klein comme ??tant contenue dans quatre dimensions.
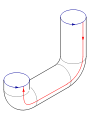
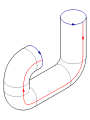
Collez les fl??ches rouges de la place ensemble (c??t??s gauche et droit), r??sultant dans un cylindre. Pour coller les extr??mit??s ensemble afin que les fl??ches sur le match cercles, passent une extr??mit?? ?? travers le c??t?? du cylindre. Notez que cela cr??e un cercle d'auto-intersection. Il se agit d'un immersion de la bouteille de Klein en trois dimensions.
En ajoutant une quatri??me dimension de l'espace ?? trois dimensions, l'auto-intersection peut ??tre ??limin??e. Peu ?? peu pousser un morceau du tube contenant l'intersection de l'espace de trois dimensions d'origine. Une analogie utile est de consid??rer une courbe d'auto-intersection sur le plan; auto-intersections peuvent ??tre ??limin??s en soulevant un brin de l'avion.
Cette immersion est utile pour visualiser de nombreuses propri??t??s de la bouteille de Klein. Par exemple, la bouteille n'a pas de limite Klein, o?? la surface se arr??te brusquement, et il est non-orientable, comme en t??moigne l'unilat??ralit?? de l'immersion.

Le mod??le physique commun d'une bouteille de Klein est une construction similaire. Le British Science Museum a expos?? une collection de verre souffl?? ?? la main des bouteilles Klein, pr??sentant de nombreuses variations sur ce th??me topologique. Les bouteilles datent de 1995 et ont ??t?? faites pour le mus??e par Alan Bennett. Clifford Stoll, auteur de L'Oeuf du Coucou, fabrique des bouteilles Klein et les vend via l' Internet au Bouteille Acme Klein.
Propri??t??s
La bouteille de Klein peut ??tre consid??r?? comme un Faisceau de fibres de la mani??re suivante: on prend la place de dessus ??tant ??gal ?? E, l'espace total, tandis que l'espace de base B est donn??e par l'intervalle unitaire en x, et la projection π est donn??e par π (x, y) = x. Depuis les deux extr??mit??s de l'intervalle unitaire dans x sont identifi??s, l'espace de base B est en fait le cercle S 1, et ainsi de la bouteille de Klein est la torsad??e S 1 -bundle ( cercle paquet) sur le cercle.
Comme le Ruban de M??bius, la bouteille de Klein est un diff??rentiable deux dimensions collecteur qui ne est pas orientable. Contrairement ?? la bande de M??bius, la bouteille de Klein est un collecteur ferm??, ce qui signifie qu'il est un compact collecteur sans limite. Alors que la bande de M??bius peut ??tre int??gr?? dans trois dimensions espace euclidien R 3, la bouteille de Klein ne peut pas. Il peut toutefois ??tre int??gr?? dans R 4,.
Le flacon peut ??tre r??alis?? Klein (au sens math??matique, car il ne peut pas se faire sans permettre ?? la surface de se coupent) en joignant les bords de deux bandes de M??bius ensemble, comme d??crit dans ce qui suit anonyme Limerick :
- Un math??maticien du nom de Klein
- Pensait que le ruban de M??bius ??tait divin.
- Il a dit: "Si vous colle
- Les bords des deux,
- Vous obtiendrez une bouteille bizarre comme le mien ".
Il peut ??galement ??tre r??alis?? par pliage d'une bande de M??bius en deux sur la longueur et ?? fixer le bord lui-m??me.
Six couleurs suffisent pour colorier ne importe quelle carte sur la surface d'une bouteille de Klein; ce est la seule exception ?? la Conjecture Heawood, une g??n??ralisation du th??or??me des quatre couleurs , ce qui n??cessiterait sept.
Une bouteille de Klein est ??quivalente ?? une sph??re plus deux bonnets crois??s.
Dissection
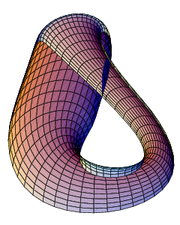
Dissection d'une bouteille de Klein en deux moiti??s le long de son plan de sym??trie r??sulte deux en miroir bandes de M??bius, ce est ?? dire une avec un demi-tour ?? gauche et l'autre avec un demi-tour ?? droite (l'un d'eux est illustr?? sur la droite). Rappelez-vous que l'intersection photo ne est pas vraiment l??. En fait, il est ??galement possible de couper la bouteille de Klein en un seul ruban de M??bius.
Param??trage

La ??figure 8?? immersion de la bouteille de Klein a un param??trage particuli??rement simple:
Dans cette immersion, le cercle d'auto-intersection g??om??trique est un cercle dans le plan xy. Le r constante positive est le rayon de ce cercle. Le param??tre u donne l'angle dans le plan xy, et c indique la position autour de la section transversale en forme de huit.
Le param??trage de l'immersion en 3 dimensions de la bouteille elle-m??me est beaucoup plus compliqu??. Voici une version simplifi??e:
o??
pour 0 ≤ u <2π et 0 ≤ v <2π.
Dans ce param??trage, u r??sulte de la longueur du corps de la bouteille tandis que v va autour de sa circonf??rence.
G??n??ralisations
La g??n??ralisation de la bouteille de Klein ?? la hausse genre est donn??e dans l'article sur la polygone fondamental.
Surface Klein
Une surface Klein est, comme pour les surfaces de Riemann , une surface avec un atlas permettant que le fonctions de transition peuvent ??tre compos??es avec complexe conjugaison peut obtient ce qu'on appelle la structure dianalytic.