Espace compact

En math??matiques , un sous-ensemble de l'espace euclidien R ⁿ est appel?? compacte si elle est ferm?? et d??limit??e. Par exemple, dans R, ferm?? le intervalle [0, 1] est compact, mais l'ensemble des entiers Z ne est pas (elle ne est pas d??limit??e) et ne est la pause de la mi-ouverte [0, 1) (il ne est pas ferm??).

Une approche plus moderne consiste ?? appeler un espace topologique compact si chacun de ses capots ouverts a une sous-couverture finie. Le Heine-Borel th??or??me montre que cette d??finition est ??quivalente ?? "ferm?? et born???? pour des sous-ensembles de l'espace euclidien.

Remarque: Certains auteurs tels que Bourbaki utiliser le terme ??quasi-compact" ?? la place, et r??server le terme "compact" pour les espaces topologiques qui sont S??par?? et ??quasi-compact". Un ensemble compact simple est parfois consid??r?? comme un compactum; suite ?? la latine seconde d??clinaison (neutre), la forme plurielle correspondante est compacta.

Histoire et la motivation

Le terme a ??t?? introduit par compacte Fr??chet en 1906 .

Il est reconnu depuis longtemps que la propri??t?? comme compacit?? est n??cessaire de prouver de nombreux th??or??mes utiles. Il fut un temps que "compact" signifiait "s??quentiellement compacte" (chaque s??quence a une suite convergente). Ce est alors principalement espaces m??triques ont ??t?? ??tudi??s. La d??finition de ??couvrant compact" est devenue plus importante parce qu'elle nous permet de consid??rer les espaces topologiques g??n??raux, et la plupart des anciens r??sultats sur les espaces m??triques peut ??tre g??n??ralis??e ?? ce param??tre. Cette g??n??ralisation est particuli??rement utile dans l'??tude de espaces de fonctions, dont beaucoup ne sont pas des espaces m??triques.

L'une des principales raisons pour ??tudier les espaces compacts est parce qu'ils sont ?? certains ??gards tr??s similaires ?? ensembles finis: il ya beaucoup de r??sultats qui sont faciles ?? montrer pour ensembles finis, dont les preuves emporterez avec des changements minimes aux espaces compacts. On dit souvent que ??compacit?? est la prochaine meilleure chose ?? finitude". Voici un exemple:

• Supposons que X est un Espace s??par??, et nous avons un point x dans X et une partie finie A de X ne contenant pas x. Ensuite, nous pouvons x s??par??e et un par quartiers: pour chaque a dans A, soit u (x) et V (a) soient quartiers disjoints contenant x et un, respectivement. Puis l'intersection de tous les U (x) et l'union de tous les V (a) sont les quartiers exig??e de x et A.

Notez que si A est infinie, la preuve ??choue, parce que l'intersection de arbitrairement de nombreux quartiers de x pourrait ne pas ??tre un voisinage de x. La preuve peut ??tre "sauv??", cependant, si A est compact: nous prenons simplement une sous-couverture finie de la couverture {V (a)} de A. De cette fa??on, nous voyons que dans un espace s??par??, ne importe quel point peut ??tre s??par?? par des quartiers de tout ensemble compact ne en contenant pas. En fait, en r??p??tant l'argument montre que les deux ensembles compacts disjoints dans un espace s??par?? peuvent ??tre s??par??s par quartiers - ?? noter que ce est pr??cis??ment ce que nous obtenons si nous rempla??ons ??point?? (c.-??- singleton set) avec "compact" dans le s??par?? s??paration axiome. Beaucoup des arguments et des r??sultats dans des espaces compacts suivent un tel motif.

D??finitions

Compacit?? des sous-ensembles de R ⁿ

Pour tout sous-ensemble de l'espace euclidien R ^n, les quatre conditions suivantes sont ??quivalentes:

• Chaque couvercle ouvert a un fini sous-couverture. Ce est la d??finition la plus couramment utilis??e.
• Chaque s??quence dans l'ensemble a une suite convergente, dont le point limite appartient ?? l'ensemble.
• Chaque sous-ensemble infini de l'ensemble a une point d'accumulation dans l'ensemble.
• L'ensemble est ferm?? et d??limit??e. Ce est la condition qui est plus facile ?? v??rifier, par exemple, un ferm?? intervalle ou ferm?? n -Ball.

En d'autres espaces, ces conditions peuvent ??tre ou ne pas ??tre ??quivalents, en fonction des propri??t??s de l'espace.

Notez que bien que la compacit?? est une propri??t?? de l'ensemble lui-m??me (avec sa topologie), closedness est relatif ?? un espace, il est en; ci-dessus "ferm??" est utilis?? dans le sens de la fermeture dans R ^n. Un ensemble qui est ferm?? par exemple Q ⁿ est g??n??ralement pas ferm?? dans R ^n, donc pas compact.

Compacit?? des espaces topologiques

Le "sous-couverture finie" propri??t?? de l'alin??a pr??c??dent est plus abstrait que le ??ferm?? et born??", mais il a l'avantage qu'il peut ??tre donn?? en utilisant le Topologie induite sur un sous-ensemble de R ^n, ce qui ??limine la n??cessit?? d'utiliser une m??trique ou un espace ambiant. Ainsi, la compacit?? est une propri??t?? topologique. Dans un sens, l'intervalle unit?? ferm??e [0,1] est intrins??quement compacte, peu importe comment il est int??gr?? dans R ou R ^n.

Un espace topologique X est d??fini comme compact si toutes ses housses ouverts ont une sous-couverture finie. Formellement, cela signifie que

pour chaque collection arbitraire 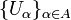de sous-ensembles ouverts de 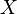tel que , Il existe une partie finie tel que .

Une d??finition ??quivalente souvent utilis?? est donn??e en termes de propri??t?? intersection finie: si ne importe quelle collection d'ensembles ferm??s satisfaisant la propri??t?? intersection finie a intersection non vide, l'espace est compact. Cette d??finition est duale de l'habituel d??clar?? en termes d'ensembles ouverts.

Certains auteurs demandent qu'un espace compact aussi ??tre S??par??, et la version non-s??par?? est ensuite appel??e quasicompact.

Des exemples d'espaces compacts

• Tout espace topologique fini, y compris le ensemble vide, est compact. L??g??rement plus g??n??ralement, ne importe quel espace avec un topologie finie (qu'un nombre fini de ensembles ouverts) est compact; ce qui inclut notamment la topologie triviale.
• Le ferm?? intervalle unitaire est compact. Cela d??coule de la Th??or??me de Heine-Borel; prouver ce th??or??me est ?? peu pr??s aussi difficile que de prouver directement que est compact. L'intervalle ouvert 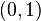ne est pas compacte: la couvercle ouvert 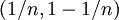pour n'a pas de sous-couverture finie.
• Pour chaque nombre naturel n, le n - sph??re est compact. Encore une fois du th??or??me Heine-Borel, la boule unit?? ferm??e de toute dimension finie espace vectoriel norm?? est compact. Ce ne est pas vrai pour les dimensions infinies; en fait, un espace vectoriel norm?? est de dimension finie si et seulement si son boule unit?? ferm??e est compact.
• Le Cantor ensemble est compact. Depuis la p entiers -adiques sont hom??omorphe ?? l'ensemble de Cantor, ils forment aussi un ensemble compact. Depuis un ensemble fini contenant des ??l??ments de p est compact, ce qui montre que le d??nombrable produit d'ensembles finis est compact, et est donc un cas particulier de Th??or??me de Tykhonov.
• Consid??rons l'ensemble 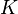de toutes les fonctions ?? partir de la droite r??elle de nombre de l'intervalle de l'unit?? de fermeture, et d??finir une topologie sur 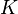de sorte qu'une s??quence en 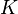converge vers 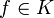si et seulement si 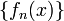converge vers 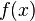pour tous 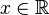. Il ya seulement une telle topologie; il est appel?? le topologie de la convergence simple. Puis 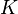est un espace topologique compact, encore une cons??quence du th??or??me de Tychonoff.
• Consid??rons l'ensemble 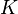de toutes les fonctions satisfaisant la Condition de Lipschitz 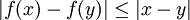pour tous et envisager sur 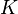la m??trique induite par la distance uniforme . Puis par Ascoli-Arzel?? th??or??me l'espace 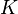est compact.
• Tout espace portant le topologie cofini est compact.
• Tout localement compact espace s??par?? peut ??tre transform?? en un espace compact en ajoutant un point unique ?? elle, par le biais de Alexandroff compactifi??. Le compactifi?? de est hom??omorphe au cercle 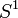; celui-compactifi?? de 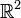est hom??omorphe ?? la sph??re 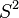. Utilisation de la compactifi??, on peut ??galement facilement construire des espaces compacts qui ne sont pas s??par??, en commen??ant par un espace non-s??par??.
• Le spectre de toute continu op??rateur lin??aire sur une Espace de Hilbert est un compact du nombre complexe C. Si l'espace de Hilbert est de dimension infinie, alors ne importe quel sous-ensemble compact de C se pr??sente de cette mani??re, que le spectre de certaines op??rateur lin??aire continue sur l'espace de Hilbert.
• Le spectre d'un anneau commutatif ou Alg??bre de Boole est compact.
• Le Hilbert cube est compact.
• Le bon ordre ou topologie gauche topologie de commande sur toute d??limit??e ensemble totalement ordonn?? est compact. En particulier, L'espace de Sierpinski est compact.
• Le Premier spectre d'un anneau commutatif avec le Topologie de Zariski est un espace compact, important dans g??om??trie alg??brique. Ces spectres premiers sont presque jamais Espaces Hausdorff.

Th??or??mes

Certains th??or??mes li??s ?? la compacit?? (voir la Topologie glossaire pour les d??finitions):

• Un image continue d'un espace compact est compact.
• Le th??or??me de la valeur extr??me: une fonction num??rique continue sur un espace compact non vide est born??e et atteint sa borne sup??rieure.
• Un sous-ensemble ferm?? d'un espace compact est compact.
• Un sous-ensemble compact d'un Espace s??par?? est ferm??.
• Un sous-ensemble compact non vide des nombres r??els a un plus grand ??l??ment et un ??l??ment moins.
• Un sous-ensemble de euclidien n -espace est compact si et seulement si il est ferm?? et born??. ( Th??or??me de Heine-Borel)
• Un espace m??trique (ou espace uniforme) est compact si et seulement si il est compl??te et totalement d??limit??e.
• Le produit de ne importe quelle collection d'espaces compacts est compact. ( Th??or??me de Tykhonov, ce qui ??quivaut ?? la axiome du choix)
• Un espace s??par?? est compacte normal.
• Chaque carte continue ?? partir d'un espace compact ?? un espace s??par?? est ferm?? et bon. Il se ensuit que tous continu bijection d'un espace compact pour un espace s??par?? est un hom??omorphisme .
• Un espace m??trique (ou plus g??n??ralement tout premi??re d??nombrable espace uniforme) est compact si et seulement si chaque s??quence dans l'espace a une s??quence convergente.
• Un espace topologique est compact si et seulement si tous les net sur l'espace a un sous-r??seau convergent.
• Un espace topologique est compact si et seulement si tous les filtre sur l'espace a un raffinement convergente.
• Un espace topologique est compact si et seulement si tous les ultrafiltre sur l'espace est convergente.
• Un espace topologique peut ??tre int??gr?? dans un espace s??par?? compact si et seulement si ce est un Espace compl??tement r??gulier.
• Chaque espace topologique X est un sous-espace dense d'un espace compact qui poss??de au plus un point de plus que X. ( Alexandroff compactifi??)
• Si l'espace m??trique X est compact et un recouvrement ouvert de X est donn??e, alors il existe un certain nombre δ> 0 tel que chaque sous-ensemble de X de diam??tre <δ est contenue dans un membre de la couverture. ( Le num??ro de Lebesgue lemme)
• Si un espace topologique a un sous-base de sorte que chaque couverture de l'espace par les membres de la sous-base a une sous-couverture finie, l'espace est compact. ( Th??or??me de sous-base de Alexander)
• Deux espaces compacts s??par?? X ₁ et X ₂ sont hom??omorphes si et seulement si leur anneaux de continus ?? valeurs r??elles fonctions C (X ₁₎ et C (X ₂₎ sont isomorphe. ( Th??or??me de Gelfand-Naimark)

D'autres formes de compacit??

Il ya un certain nombre de propri??t??s topologiques qui sont ??quivalentes ?? compacit?? espaces m??triques, mais sont non ??quivalents dans les espaces topologiques g??n??raux. Ceux-ci comprennent les suivantes.

• S??quentiellement compacte: Chaque s??quence a une suite convergente.
• Semi-compact: Chaque couvercle ouvert d??nombrable a une sous-couverture finie. (Ou, ce qui revient, chaque sous-ensemble infini a un point ω-accumulation.)
• Pseudocompact: Chaque valeur r??elle continue fonction de l'espace est limit??.
• Faiblement semi-compact (ou point limite compact): Chaque sous-ensemble infini a une point d'accumulation.

Si toutes ces conditions sont ??quivalentes pour espaces m??triques, en g??n??ral, nous ont les implications suivantes:

• Espaces compacts sont semi-compact.
• S??quentiellement espaces compacts sont semi-compact.
• D??nombrable espaces compacts sont pseudocompact et faiblement semi-compact.

Non chaque espace semi-compact est compact; un exemple est donn?? par le premier ordinal d??nombrable ?? l'ordre topologie. Non chaque espace compact est s??quentiellement compacte; un exemple est donn?? par deux ^[0,1], de la topologie du produit.

Un espace m??trique est appel??e pr??-compacte ou le cas ??ch??ant totalement d??limit?? s??quence a une s??quence de Cauchy; cela peut ??tre g??n??ralis??e ?? espaces uniformes. Pour les espaces m??triques complets ce qui ??quivaut ?? la compacit??. Voir relativement compact pour la version topologique.

Une autre notion li??e qui (par la plupart des d??finitions) est strictement plus faible que la compacit?? est compacit?? locale.