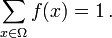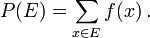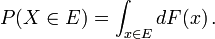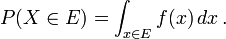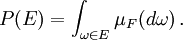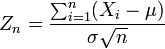La th??orie des probabilit??s

Saviez-vous ...

SOS croit que l'??ducation donne une meilleure chance dans la vie des enfants dans le monde en d??veloppement aussi. Avec enfants SOS vous pouvez choisir de parrainer des enfants dans plus de cent pays

La th??orie des probabilit??s est la branche de math??matiques concern??s par l'analyse des ph??nom??nes al??atoires. Les objets centraux de la th??orie des probabilit??s sont variables al??atoires , processus stochastiques et ??v??nements: abstractions math??matiques ??v??nements non d??terministes ou les quantit??s mesur??es qui peuvent ??tre soit occurrences uniques ou ??voluer au fil du temps de fa??on apparemment al??atoire. Bien qu'une pi??ce individuelle jeter ou le rouleau d'un d?? est un ??v??nement al??atoire, se il est r??p??t?? de nombreuses fois la s??quence des ??v??nements al??atoires pr??sente certaines tendances statistiques, qui peuvent ??tre ??tudi??s et pr??visibles. Deux r??sultats math??matiques repr??sentatifs d??crivant ces mod??les sont les loi des grands nombres et le th??or??me central limite.

En tant que fondation math??matique pour les statistiques , la th??orie des probabilit??s est essentielle pour de nombreuses activit??s humaines qui impliquent l'analyse quantitative de grands ensembles de donn??es. M??thodes de la th??orie des probabilit??s se appliquent ??galement ?? la description des syst??mes complexes donn??s qu'une connaissance partielle de leur ??tat, comme dans la m??canique statistique . Une grande d??couverte de XXe si??cle la physique ??tait la nature probabiliste des ph??nom??nes physiques ?? des ??chelles atomiques, d??crites dans la m??canique quantique .

Histoire

La th??orie math??matique de probabilit?? a ses racines dans les tentatives pour analyser jeux de hasard par J??r??me Cardan au XVIe si??cle, et par Pierre de Fermat et Blaise Pascal au XVIIe si??cle (par exemple le " probl??me de points ").

Initialement, la th??orie des probabilit??s principalement consid??r?? ??v??nements discrets, et ses m??thodes ??taient essentiellement combinatoire . Finalement, analytiques consid??rations ont amen?? l'int??gration de variables continues dans la th??orie. Ce abouti ?? la th??orie moderne des probabilit??s, les fondations de ce qui ont ??t?? port??es par Andrey Nikolaevich Kolmogorov. Kolmogorov associ?? la notion de l'espace ??chantillon, introduit par Richard von Mises, et th??orie de la mesure et a pr??sent?? ses syst??me d'axiomes de la th??orie des probabilit??s en 1933. Assez rapidement ce est devenu le leader incontest?? base axiomatique de la th??orie moderne des probabilit??s.

Traitement

La plupart des introductions ?? la th??orie des probabilit??s traitent des distributions de probabilit??s discr??tes et les distributions de probabilit??s continues s??par??ment. Le traitement plus math??matiquement avanc?? bas?? th??orie de la mesure de la probabilit?? couvre ?? la fois discret, continu, ne importe quel m??lange de ces deux et plus encore.

Distributions de probabilit?? discr??tes

La th??orie des probabilit??s discr??te traite avec des ??v??nements qui se produisent dans espaces d'??chantillons d??nombrables.

Exemples: Lancer des d??s , des exp??riences avec jeux de cartes , et marche al??atoire.

D??finition classique: Initialement, la probabilit?? d'un ??v??nement de se produire a ??t?? d??finie comme le nombre de cas favorables pour l'??v??nement, sur le nombre de r??sultats possibles au total dans un espace de l'??chantillon ??quiprobable.

Par exemple, si l'??v??nement est "apparition d'un nombre pair quand une matrice est roul?? ??, la probabilit?? est donn??e par 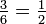$\ Frac {3} {6} = \ frac {1} {2}$ , Depuis trois faces sur 6 ont nombres pairs et chaque face a la m??me probabilit?? d'appara??tre.

D??finition moderne: la d??finition moderne commence avec un jeu appel?? l'espace de l'??chantillon, qui se rapporte ?? l'ensemble de tous les r??sultats possibles en sens classique, not??e $\ Omega = \ \ left {x_1, x_2, \ dots \ right \}$ . On suppose alors que pour chaque ??l??ment $x \ in \ Omega \,$ , Une valeur intrins??que "de probabilit??" $f (x) \,$ est fix??, ce qui satisfait les propri??t??s suivantes:

$f (x) \ in [0,1] \ mbox {} pour tous les x \ in \ Omega \ ,;$
$\ {X sum_ \ in \ Omega} f (x) = 1 \ ,.$

Autrement dit, la fonction de probabilit?? f (x) se situe entre z??ro et un pour chaque valeur de x dans la Ω spatiale de l'??chantillon et la somme de f (x) sur toutes les valeurs x dans le Ω d'espace d'??chantillon est exactement ??gale ?? 1. ??v??nement est d??fini comme tout sous-ensemble 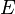$E \,$ de l'espace d'??chantillon 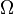$\ Omega \,$ . La probabilit?? de l'??v??nement 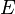$E \,$ d??fini comme

$P (E) = \ {x sum_ \ E} f (x) \ ,.$

Ainsi, la probabilit?? de l'espace d'??chantillon entier est 1, et la probabilit?? de l'??v??nement nulle est 0.

La fonction $f (x) \,$ mappage d'un point dans l'espace d'??chantillon ?? la valeur de "probabilit??" est appel??e Fonction de masse abr??g?? en pmf. La d??finition moderne ne cherche pas ?? r??pondre ?? la fa??on dont les fonctions de masse de probabilit?? sont obtenus; se appuie au contraire une th??orie qui suppose leur existence.

Distributions de probabilit??s continues

La th??orie de la probabilit?? continue traite avec des ??v??nements qui se produisent dans un espace de l'??chantillon continue.

D??finition classique: La d??finition classique se d??compose lorsqu'il est confront?? ?? l'affaire continue. Voir Le paradoxe de Bertrand.

D??finition moderne: Si l'espace de l'??chantillon est les nombres r??els ( $\ Mathbb {R}$ ), Alors une fonction appel??e fonction de r??partition (ou cdf) $F \,$ est suppos?? exister, ce qui donne 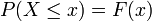$P (X \ le x) = F (x) \,$ pour une variable al??atoire X. Ce est, F (x) renvoie la probabilit?? que X sera inf??rieur ou ??gal ?? x.

Le CDF doit satisfaire les propri??t??s suivantes.

$F \,$ est un monotone non d??croissante, fonction continue ?? droite;
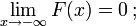
$\ {X lim_ \ rightarrow - \ infty} F (x) = 0 \ ,;$
$\ {X lim_ \ rightarrow \ infty} F (x) = 1 \ ,.$

Si $F \,$ est diff??rentiables, alors la variable al??atoire X est dit d'avoir un fonction de densit?? de probabilit?? ou pdf ou simplement densit?? $f (x) = \ frac {dF (x)} {dx} \ ,.$

Pour un ensemble 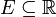$E \ subseteq \ mathbb {R}$ , La probabilit?? de la variable al??atoire X ??tant 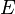$E \,$ est d??fini comme ??tant

$P (X \ in E) = \ {x int_ \ E} dF (x) \ ,.$

Dans le cas o?? la fonction de densit?? de probabilit?? existe, ce qui peut se ??crire

$P (X \ in E) = \ {x int_ \ E} f (x) \, dx \ ,.$

Alors que le pdf ne existe que pour les variables al??atoires continues, la fonction de r??partition existe pour toutes les variables al??atoires (y compris les variables al??atoires discr??tes) qui prennent des valeurs sur $\ Mathbb {R} \ ,.$

Ces concepts peuvent ??tre g??n??ralis??s pour cas multidimensionnels sur 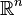$\ Mathbb {R} ^ n$ et autres espaces d'??chantillons en continu.

La th??orie des probabilit??s Mesurer la th??orie

La raison d'??tre du traitement de la probabilit?? mesure la th??orie est qu'il unifie le discret et continu, et fait la diff??rence une question de mesure utilis??e. De plus, elle couvre les distributions qui ne sont ni des m??langes discrets continus ni ni des deux.

Un exemple d'une telle distribution peut ??tre un m??lange de distributions discr??tes et continues, par exemple, une variable al??atoire qui est ??gal ?? 0 avec une probabilit?? de 1/2, et prend une valeur de distribution normale al??atoire avec une probabilit?? de 1/2. Il peut encore ??tre ??tudi?? dans une certaine mesure en le consid??rant d'avoir un pdf $(\ Delta [x] + \ varphi (x)) / 2$ O?? $\ Delta [x]$ est le Fonction delta Kronecker.

Autres distributions peuvent m??me ne pas ??tre un m??lange, par exemple, le Loi de Cantor a aucune probabilit?? positive pour un point unique, ni ne ont une densit??. L'approche moderne de la th??orie des probabilit??s permet de r??soudre ces probl??mes en utilisant th??orie de la mesure de d??finir l' espace de probabilit?? :

Compte tenu de tout ensemble 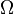$\ Omega$ , (??galement appel?? l'espace de l'??chantillon) et un σ-alg??bre 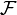$\ Mathcal {F} \,$ sur elle, un mesurer 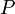$P$ est appel?? une mesure de probabilit?? si

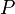$P \,$ est non n??gatif;
$P (\ Omega) = 1 \ ,.$

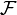Si $\ Mathcal {F} \,$ est un -Alg??bre de Borel puis il ya une mesure de probabilit?? unique sur 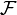$\ Mathcal {F} \,$ pour toute cdf, et vice versa. La mesure correspondant ?? une fonction de r??partition est dit ??tre induite par le CDF. Cette mesure co??ncide avec le PMF pour les variables discr??tes, et pdf pour les variables continues, ce qui rend l'approche de mesure th??orie sans illusions.

La probabilit?? d'un ensemble 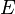$E \,$ dans la σ-alg??bre 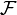$\ Mathcal {F} \,$ est d??fini comme ??tant

$P (E) = \ int _ {\ omega \ E} \ mu_F (d \ omega) \ ,.$

o?? l'int??gration est par rapport ?? la mesure $\ Mu_F \,$ induite par $F \ ,.$

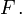
En plus de fournir une meilleure compr??hension et ?? l'unification des probabilit??s discr??tes et continues, le traitement de mesure th??orie nous permet ??galement de travailler sur des probabilit??s ext??rieur 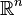$\ Mathbb {R} ^ n$ , Comme dans la th??orie de processus stochastiques. Par exemple, pour ??tudier Mouvement brownien, la probabilit?? est d??finie sur un espace de fonctions.

Les distributions de probabilit??s

Certaines variables al??atoires se produisent tr??s souvent dans la th??orie des probabilit??s parce qu'ils d??crivent ainsi de nombreux processus naturels ou physiques. Leurs distributions ont donc pris une importance particuli??re dans la th??orie des probabilit??s. Certaines distributions discr??tes fondamentales sont uniforme discr??te, Bernoulli, binomiale , binomiale n??gative, Poisson et distributions g??om??triques. Distributions continues importants comprennent le continue et uniforme, normale , exponentielle , gamma et distributions b??ta.

Convergence des variables al??atoires

Dans la th??orie des probabilit??s, il ya plusieurs notions de convergence pour des variables al??atoires . Ils sont ??num??r??s ci-dessous dans l'ordre de la force, ce est ?? dire, toute notion de convergence ult??rieure dans la liste implique la convergence selon toutes les notions pr??c??dentes.

Convergence dans la distribution: Comme son nom l'indique, une s??quence de variables al??atoires 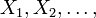$X_1, X_2, \ dots, \,$ converge vers la variable al??atoire $X \,$ dans la distribution si leurs fonctions de r??partition respectives $F_1, F_2, \ dots \,$ converger vers la fonction de distribution cumulative $F \,$ de $X \,$ , O?? $F \,$ est continue.

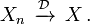
La plupart notation commune de main courte: $X_n \, \ xrightarrow {\ mathcal D} \, X \ ,.$

Convergence faible: La s??quence de variables al??atoires 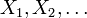$X_1, X_2, \ dots \,$ est dit ?? converger vers la variable al??atoire $X \,$ si faiblement $\ Lim_ {n \ rightarrow \ infty} P \ gauche (\ left | X_n-X \ right | \ geq \ varepsilon \ right) = 0$ pour chaque ε> 0. Convergence faible est aussi appel?? la convergence en probabilit??.

La plupart notation commune de main courte: $X_n \, \ xrightarrow {P} \, X \ ,.$

Forte convergence: La s??quence de variables al??atoires 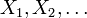$X_1, X_2, \ dots \,$ est dit ?? converger vers la variable al??atoire $X \,$ si fortement $P (\ lim_ {n \ rightarrow \ infty} X_n = X) = 1$ . Forte convergence est ??galement connu comme convergence presque s??re.

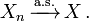
La plupart notation commune de main courte: $X_n \, \ {\ mathrm xrightarrow {A.ş.}} \, X \ ,.$

Intuitivement, une forte convergence est une version plus puissante de la convergence faible, et dans les deux cas, les variables al??atoires 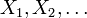$X_1, X_2, \ dots \,$ montrent une corr??lation croissante avec $X \,$ . Cependant, en cas de convergence dans la distribution, les valeurs r??alis??es des variables al??atoires ne ont pas ?? converger, et une corr??lation possible entre eux est sans importance.

Loi des grands nombres

Intuition commune sugg??re que si une pi??ce de monnaie est lanc??e ?? plusieurs reprises, puis ?? peu pr??s la moiti?? du temps il va tourner des t??tes, et l'autre moiti??, il se retrouvera queues. En outre, plus souvent le pi??ce est lanc??e, plus il devrait ??tre que le rapport du nombre de t??tes au nombre de queues se approchera unit??. Probabilit?? moderne fournit une version officielle de cette id??e intuitive, connu comme la loi des grands nombres. Cette loi est remarquable parce qu'il ne est nulle part suppos?? dans les fondements de la th??orie des probabilit??s, mais ??merge place sur ces fondations comme un th??or??me. Depuis il relie probabilit??s d??riv??es th??oriquement ?? leur fr??quence r??elle dans le monde r??el, la loi des grands nombres est consid??r?? comme un pilier de l'histoire de la th??orie statistique.

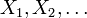La loi des grands nombres (LLN) indique que la moyenne de l'??chantillon $\ Overline {X} _n = \ tfrac1n {\ sum X_n}$ de $X_1, X_2, \ dots \,$ (Ind??pendants et identiquement distribu??s variables al??atoires attente finie 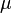$\ mu$ ) Converge vers l'attente th??orique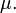 $\ Mu.$

Ce est dans les diff??rentes formes de convergence des variables al??atoires qui s??pare le faible et le fort loi des grands nombres

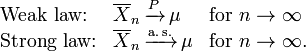
$\ Begin {array} {lll} \ text {Loi faible:} et \ overline {X} _n \, \ xrightarrow {P} \, \ mu & \ text {for} n \ to \ infty \\ \ text {Forte la loi:} et \ overline {X} _n \, \ xrightarrow {\ mathrm {a \, s..}} \, \ mu & \ text {for} n \ to \ infty. \ End {array}$

Il r??sulte de LLN que si un ??v??nement de probabilit?? p est observ?? ?? plusieurs reprises au cours d'exp??riences ind??pendantes, le rapport de la fr??quence observ??e de cet ??v??nement au nombre total de r??p??titions converge vers p.

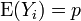Mettre cela en termes de variables al??atoires et nous avons LLN $Y_1, Y_2, ... \,$ sont ind??pendants Variables al??atoires de Bernoulli prenant des valeurs avec une probabilit?? p et 0 avec une probabilit?? 1- p. $\ Textrm {E} (y_i) = p$ pour tout i et il se ensuit que de LLN 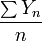$\ Frac {\ sum y_n} {n} \,$ converge vers p presque s??rement.

Th??or??me central limite

Le th??or??me central limite explique l'omnipr??sence de la distribution normale dans la nature; il est l'un des plus c??l??bres th??or??mes en probabilit??s et statistiques.

Le th??or??me affirme que la moyenne de nombreuses variables al??atoires ind??pendantes et identiquement distribu??es avec variance finie tend vers une distribution normale , ind??pendamment de la r??partition suivie par les variables al??atoires originaux. Formellement, soit 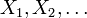$X_1, X_2, \ dots \,$ ??tre des variables al??atoires ind??pendantes de moyenne 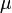$\ Mu_ \,$ et variance 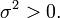$\ Sigma ^ 2> 0 \,$ Ensuite, la s??quence de variables al??atoires

$Z_n = \ frac {\ sum_ {i = 1} ^ n (X_i - \ mu)} {\ sigma \ sqrt {n}} \,$

converge en distribution ?? une normale standard variable al??atoire.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Probability_theory&oldid=226584914 "