Espace de probabilit??

La d??finition de l'espace de probabilit?? est le fondement de la th??orie des probabilit??s . Il a ??t?? introduit par Kolmogorov dans la 1930. Pour une alternative alg??brique pour l'approche de Kolmogorov, voir alg??bre des variables al??atoires.

D??finition

Un espace de probabilit?? 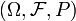est un mesure l'espace avec une mesure P qui satisfait la axiomes de probabilit??.

L'espace de l'??chantillon est non vide ensemble dont les ??l??ments sont connus comme les r??sultats ou les ??tats de la nature et sont souvent donn?? le symbole 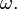L'ensemble de tous les r??sultats possibles d'une exp??rience est connu que l'espace de l'exp??rience de l'??chantillon.

??v??nements

Le deuxi??me ??l??ment, 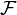, Est un σ-alg??bre des sous-ensembles de 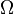. Ses ??l??ments sont appel??s ??v??nements, qui sont des ensembles de r??sultats pour lesquels on peut poser une probabilit??.

Parce que 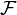est un σ-alg??bre, il contient 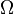; aussi, le compl??ment de tout ??v??nement est un ??v??nement, et le syndicat de toute s??quence (fini ou infini d??nombrable) des ??v??nements est un ??v??nement.

Habituellement, les ??v??nements sont la Lebesgue-mesurable ou Borel-ensembles mesurables de nombres r??els.

Mesure probabilit??

La mesure de probabilit?? 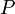est une fonction ?? partir de 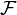pour les nombres r??els qui attribue ?? chaque ??v??nement une probabilit?? comprise entre 0 et 1. Il doit satisfaire la axiomes de probabilit??.

Parce que 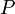est une fonction d??finie sur 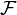et pas sur 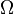, L'ensemble des ??v??nements ne est pas n??cessaire d'??tre le compl??te r??gler la puissance de l'espace de l'??chantillon; ce est pas tous ensemble de r??sultats est forc??ment un ??v??nement.

Lorsque plus d'une mesure est en cours de discussion, des mesures de probabilit?? sont souvent ??crites en tableau noir gras pour les distinguer. Quand il ne est qu'une mesure de probabilit?? en cours de discussion, il est souvent d??sign?? par le Pr, ce qui signifie "probabilit?? de".

Concepts associ??s

Distribution de probabilit??

Toute distribution de probabilit?? d??finit une mesure de probabilit??.

Variables al??atoires

Une variable al??atoire X est un fonction mesurable de l'espace de l'??chantillon 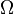; ?? un autre espace mesurable appel?? l'espace d'??tat.

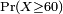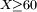Si X est un valeur r??elle variable al??atoire, alors la notation est un raccourci pour , En admettant que est un ??v??nement.

Probabilit?? conditionnelle

La d??finition de Kolmogorov des espaces de probabilit?? donne naissance au concept naturel de probabilit?? conditionnelle. Chaque ensemble avec probabilit?? non nulle (ce est-P (A) 0>) d??finit une autre mesure de probabilit??

sur l'espace. Ce est g??n??ralement interpr??t?? comme la ??probabilit?? de B Une donn??e".

Ind??pendance

Deux ??v??nements A et B sont dits ind??pendant si P (A ∩ B) = P (A) P (B).

Deux variables al??atoires, X et Y, sont cens??s ??tre ind??pendante si un ??v??nement d??fini en termes de X est ind??pendant de tout ??v??nement d??fini en termes de Y. Formellement, ils g??n??rent σ-alg??bres ind??pendante, o?? deux σ-alg??bres G et H, qui sont des sous-ensembles de F sont dites ind??pendantes si un ??l??ment de G est ind??pendante de tout ??l??ment de H.

Le concept d'ind??pendance est l?? que la th??orie des probabilit??s quitte th??orie de la mesure.

L'exclusivit?? mutuelle

Deux ??v??nements A et B sont dits mutuellement exclusives ou disjoints si P (A ∩ B) = 0. (Ceci est plus faible que A ∩ B = ∅, ce qui est la d??finition de disjoint pour les jeux).

Si A et B sont des ??v??nements disjoints, alors P (A ∪ B) = P (A) + P (B). Cela se ??tend ?? une s??quence (fini ou infini d??nombrable) des ??v??nements. Cependant, la probabilit?? de l'union d'un ensemble non d??nombrable d'??v??nements ne est pas la somme de leurs probabilit??s. Par exemple, si Z est une distribution normale variable al??atoire, alors P (Z = x) est de 0 pour tout x, mais P (Z est r??el) = 1.

L'??v??nement A ∩ B est d??sign?? par A et B, et l'??v??nement A ∪ B que A ou B.

Exemples

Premier exemple

Si l'espace concerne une chiquenaude d'un pi??ce de monnaie, puis les r??sultats sont t??tes et les queues:

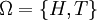
Les ??v??nements sont

• {} H: t??tes,
• {T}: queues,
• {}: Ni t??tes ni queues, et
• {H, T}: pile ou face.

Alors,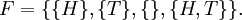

Il ya une chance de jeter soit t??te ou la queue de cinquante pour cent: P ({H}) = P ({T}) = 0,5. La chance de jeter ne est nulle: P ({}) = 0, et la chance de jeter un ou l'autre est une: P ({H, T}) = 1.

Deuxi??me exemple

Si 100 ??lecteurs doivent ??tre tir??s au hasard parmi tous les ??lecteurs de la Californie et a demand?? qui ils vont voter pour le gouverneur, alors l'ensemble de toutes les s??quences de 100 votes californiens serait le Ω de l'espace de l'??chantillon.

L'ensemble de toutes les s??quences de 100 ??lecteurs californiens dans laquelle au moins 60 vont voter pour Schwarzenegger est identifi?? avec ??l'??v??nement?? qu'au moins 60 des 100 ??lecteurs choisis allons donc voter.

Ensuite, 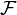contient: (1) l'ensemble de toutes les s??quences de 100 o?? au moins 60 voix pour Schwarzenegger; (2) l'ensemble de toutes les s??quences de 100 o?? moins de 60 voix pour Schwarzenegger (l'inverse de (1)); (3) l'espace Ω de l'??chantillon comme ci-dessus; et (4) l'ensemble vide.

Un exemple d'une variable al??atoire est le nombre d'??lecteurs qui vont voter pour Schwarzenegger dans l'??chantillon de 100.