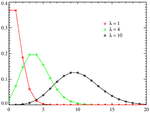
Distribution de probabilit??

Une distribution de probabilit?? d??crit les valeurs et les probabilit??s qu'une ??v??nement al??atoire peut avoir lieu. Les valeurs doivent couvrir l'ensemble des r??sultats possibles de l'??v??nement, alors que le total doit probabilit??s totaliser exactement 1, ou 100%. Par exemple, un seul coin flip peut prendre des valeurs Heads or Tails avec une probabilit?? de 1/2 exactement pour chaque; ces deux valeurs et deux probabilit??s repr??sentent la distribution de probabilit?? de l'??v??nement pi??ce de retournement unique. Cette distribution se appelle une distribution discr??te car il ya nombre d??nombrable de r??sultats discrets avec des probabilit??s positives.

Une distribution continue d??crit les ??v??nements sur une plage continue, o?? la probabilit?? d'un r??sultat sp??cifique est z??ro. Par exemple, une fl??chette lanc??e ?? un jeu de fl??chettes a essentiellement une probabilit?? nulle de l'atterrissage ?? un moment pr??cis, car un point est extr??mement faible, mais il a une certaine probabilit?? de l'atterrissage dans une zone donn??e. La probabilit?? de l'atterrissage dans la petite zone de la bulle serait (je esp??re) ??tre sup??rieur ?? l'atterrissage sur une superficie ??quivalente ailleurs sur la carte. Une fonction lisse qui d??crit la probabilit?? d'atterrir ne importe o?? sur la cible est la distribution de probabilit?? de l'??v??nement de lancement de fl??chettes. L' int??grale de la fonction de densit?? de probabilit?? (pdf) sur toute la surface de la cible (et, peut-??tre, le mur qui l'entoure) doit ??tre ??gale ?? 1, puisque chaque fl??chette doit atterrir quelque part.

Le concept de la distribution de probabilit?? et les variables al??atoires qu'ils d??crivent sous-tend la discipline math??matique de la th??orie des probabilit??s , et la science des statistiques . Il est r??parti ou de la variabilit?? dans presque ne importe quelle valeur qui peut ??tre mesur??e dans une population (par exemple taille des gens, la durabilit?? d'un m??tal, etc.); presque toutes les mesures sont faites avec une certaine erreur intrins??que; dans la physique de nombreux proc??d??s sont d??crits de mani??re probabiliste, ?? partir de la propri??t??s cin??tiques de gaz ?? la m??canique quantique description de particules fondamentales. Pour ces raisons et bien d'autres, simples num??ros sont souvent insuffisants pour d??crire une quantit??, tandis que les distributions de probabilit?? sont souvent des mod??les plus appropri??s. Il ya, cependant, des complications math??matiques dans la manipulation des distributions de probabilit??, depuis plus standard arithm??tique et manipulations alg??briques ne peuvent pas ??tre appliqu??es.

D??finitions rigoureuses

Dans la th??orie des probabilit??s , chaque variable al??atoire peut ??tre attribu??e ?? une fonction d??finie sur un espace d'??tat ??quip?? d'une distribution de probabilit?? qui assigne une probabilit?? ?? chaque sous-ensemble (plus pr??cis??ment chaque sous-ensemble mesurable) de son espace d'??tat de telle sorte que le axiomes de probabilit?? sont satisfaits. Ce est, distributions de probabilit?? sont mesures de probabilit?? d??finies sur un espace ?? la place de l'Etat de l'espace ??chantillon. Une variable al??atoire d??finit alors une mesure de probabilit?? sur l'espace de l'??chantillon en attribuant un sous-ensemble de l'espace de l'??chantillon la probabilit?? de son image inverse dans l'espace d'??tat. En d'autres termes, la distribution de probabilit?? d'une variable al??atoire est la faire avancer mesure de la distribution de probabilit?? sur l'espace d'??tat.

Les distributions de probabilit?? de variables al??atoires valeur r??elle

Parce que une distribution de probabilit?? Pr sur la ligne r??elle est d??termin??e par la probabilit?? d'??tre dans un intervalle semi-ouvert Pr (a, b], la distribution de probabilit?? d'une variable al??atoire ?? valeur r??elle X est compl??tement caract??ris??e par son fonction de distribution cumulative:

Distribution de probabilit?? discr??te

Une distribution de probabilit?? est appel?? discr??te si sa fonction de distribution cumulative ne augmente que dans les sauts.

Le ensemble des valeurs qu'une variable al??atoire discr??te peut assumer non nulle probabilit?? est soit fini ou d??nombrable infinie car la somme de ind??nombrablement nombreux positifs nombres r??els (qui est la plus petite borne sup??rieure de l'ensemble des sommes partielles finies) diverge toujours ?? l'infini. En r??gle g??n??rale, l'ensemble des valeurs possibles est topologiquement discret en ce sens que tous ses points sont points isol??s. Mais, il ya des variables al??atoires discr??tes pour lequel ce est ensemble d??nombrable dense sur la ligne r??elle.

Distributions discr??tes sont caract??ris??s par une Fonction de masse, 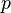tel que

La distribution de probabilit?? continue

Par une convention, une distribution de probabilit?? est appel??e en continu si sa fonction de distribution cumulative est continu, ce qui signifie qu'elle appartient ?? une variable al??atoire X pour laquelle Pr [X = x] = 0 pour tout x dans R.

Une autre convention se r??serve la distribution de probabilit?? continue ?? long terme pour distributions absolument continue. Ces distributions peuvent ??tre caract??ris??s par un fonction de densit?? de probabilit??: un non-n??gative int??grable Lebesgue fonction 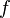d??fini sur les nombres r??els tels que

Distributions discr??tes et certaines distributions continues (comme le l'escalier du diable) ne admet pas une telle densit??.

Terminologie

Le soutien d'une distribution est le plus petit ensemble ferm?? dont le compl??ment a une probabilit?? nulle.

La distribution de probabilit?? de la somme de deux variables al??atoires ind??pendantes est le convolution de chacun de leurs distributions.

La distribution de probabilit?? de la diff??rence de deux variables al??atoires est la corr??lation crois??e de chacun de leurs distributions.

Une variable al??atoire discr??te est une variable al??atoire dont la distribution probabilit?? est discr??te. De m??me, une variable al??atoire continue est une variable al??atoire dont la loi de probabilit?? est continue.

Liste des distributions de probabilit?? importants

Certaines variables al??atoires apparaissent tr??s souvent dans la th??orie des probabilit??s, dans certains cas, en raison de leur application ?? de nombreux ph??nom??nes naturels et physiques, et dans certains cas pour des raisons th??oriques telles que la th??or??me central limite, le Poisson th??or??me de la limite ou des propri??t??s telles que Perte de m??moire ou d'un autre caract??risations. Leurs distributions ont donc pris une importance particuli??re dans la th??orie des probabilit??s.

Distributions discr??tes

Avec support fini

• Le Distribution de Bernoulli, qui prend la valeur 1 avec une probabilit?? p et la valeur 0 avec une probabilit?? q = 1 - p.
• Le Loi de Rademacher, qui prend la valeur 1 avec une probabilit?? 1/2 et la valeur -1 avec une probabilit?? 1/2.
• La distribution binomiale d??crit le nombre de succ??s dans une s??rie d'ind??pendants Oui / Non exp??riences.
• Le la distribution d??g??n??r??e en x _0, o?? X est certain de prendre la valeur ₀ x. Cela ne ressemble pas au hasard, mais il r??pond ?? la d??finition de variable al??atoire . Il est utile parce qu'il met des variables et des variables al??atoires d??terministes dans le m??me formalisme.
• Le distribution uniforme discr??te, o?? tous les ??l??ments d'un fini ensemble sont ??galement probables. Ce est cens?? ??tre la distribution d'une pi??ce ??quilibr??e, une fili??re impartiale, une roulette de casino ou un jeu bien m??lang??. Aussi, on peut utiliser des mesures de ??tats quantiques pour g??n??rer des variables al??atoires uniformes. Tous ces dispositifs sont ??m??caniques?? ??physique?? ou, sous r??serve de d??fauts de conception ou de perturbations, de sorte que la distribution uniforme ne est qu'une approximation de leur comportement. Dans les ordinateurs num??riques, g??n??rateurs de nombres pseudo-al??atoires sont utilis??es pour produire un la distribution uniforme discr??te statistiquement al??atoire.
• Le distribution hyperg??om??trique, qui d??crit le nombre de succ??s dans la premi??re m d'une s??rie de n Oui / Non exp??riences, si le nombre total de succ??s est connue.
• La loi de Zipf ou la distribution Zipf. Une distribution en loi de puissance discr??te, le plus c??l??bre exemple est la description de la fr??quence des mots dans la langue anglaise.
• Le La loi de Zipf-Mandelbrot est une distribution de loi de puissance discr??te qui est une g??n??ralisation de la La distribution Zipf.

Avec le soutien infinie

• Le Distribution de Boltzmann, une distribution discr??te important physique statistique qui d??crit les probabilit??s des diff??rents niveaux d'??nergie discrets d'un syst??me de ??quilibre thermique. Il dispose d'un analogue continu. Cas particuliers comprennent:
  • Le Distribution de Gibbs
  • Le Distribution de Maxwell-Boltzmann
  • Le La distribution de Bose-Einstein
  • Le Distribution de Fermi-Dirac
• Le distribution g??om??trique, une distribution discr??te qui d??crit le nombre de tentatives n??cessaires pour obtenir le premier succ??s dans une s??rie d'ind??pendants Oui / Non exp??riences.

Distribution de Poisson

• Le logarithmique (s??rie) la distribution
• Le distribution binomiale n??gative, une g??n??ralisation de la distribution g??om??trique de la n-i??me succ??s
• Le la distribution fractale parabolique
• La distribution de Poisson , qui d??crit un tr??s grand nombre d'??v??nements improbables individuellement qui se produisent dans un certain intervalle de temps.

Loi de Skellam

• Le Loi de Skellam, la distribution de la diff??rence entre deux variables al??atoires de Poisson ind??pendantes distribu??e
• Le Loi de Yule-Simon
• Le R??partition zeta a des utilisations en statistique appliqu??e et m??canique statistique, et peut-??tre peut ??tre d'int??r??t pour les th??oriciens des nombres. C'est le Zipf pour la distribution d'un nombre infini d'??l??ments.

Distributions continues

Pris en charge sur un intervalle born??

Loi b??ta

• Le Loi b??ta sur [0,1], dont la distribution uniforme est un cas particulier, et qui est utile dans l'estimation des probabilit??s de r??ussite.

distribution uniforme continu

• Le la distribution uniforme continue sur [a, b], o?? tous les points dans un intervalle fini sont ??galement probables.
  • Le distribution rectangulaire est une distribution uniforme sur [-1 / 2,1 / 2].
• Le Dirac bien que pas strictement une fonction, est une forme de limitation de beaucoup de fonctions continues de probabilit??. Elle repr??sente une distribution de probabilit?? discr??te concentr?? ?? 0 - un la distribution d??g??n??r??e - mais la notation traite comme se il se agissait d'une distribution continue.
• Le Loi de Kent sur la sph??re en trois dimensions
• Le Loi Kumaraswamy est aussi polyvalent que la distribution Beta mais a formes ferm??es simples ?? la fois pour la cdf et pdf.
• Le la distribution logarithmique (continue)
• Le distribution triangulaire sur [a, b], un cas particulier de ce qui est de la distribution de la somme de deux variables al??atoires r??parties uniform??ment (la convolution de deux distributions uniformes).
• Le distribution normale tronqu??e sur [a, b]
• Le Loi parabolique sur [a, b]
• Le Loi de von Mises sur le cercle
• Le Loi de von Mises-Fisher sur la sph??re ?? N dimensions a le Loi de von Mises comme un cas particulier.
• Le Loi du demi-cercle est important dans la th??orie de matrices al??atoires.

Pris en charge sur des intervalles semi-infinies, habituellement [0, ∞)

la distribution chi-carr??

• Le la distribution chi
• Le distribution chi non centrale
• La distribution chi-carr?? , qui est la somme des carr??s des variables al??atoires gaussiennes n ind??pendants. Ce est un cas particulier de la distribution Gamma, et il est utilis?? dans tests dans la bont?? de l'ajustement des statistiques .
  • Le Inverse Chi-carr?? de distribution
  • Le chi carr?? non centrale de distribution
  • Le ??chelle inverse chi carr?? la distribution

Distribution exponentielle

• La distribution exponentielle , qui d??crit le temps entre des ??v??nements al??atoires rares cons??cutives dans un processus sans m??moire.
• Le F-distribution, qui est la distribution du rapport de deux variables al??atoires (normalis??) chi-carr??s r??partis, utilis?? dans le analyse de la variance. (Appel?? Loi b??ta prime quand il est le rapport de deux variables chi-carr?? qui ne sont pas normalis??s en les divisant par le nombre de leurs degr??s de libert??.)
  • Le F non centrale de distribution

Distribution Gamma

• Le Distribution Gamma, qui d??crit le temps jusqu'?? ce que des ??v??nements al??atoires n rares cons??cutifs se produisent dans un processus sans m??moire.
  • Le Distribution d'Erlang, qui est un cas particulier de la distribution gamma avec le param??tre de forme int??grale, d??velopp?? pour pr??dire les temps d'attente dans syst??mes de files d'attente.
  • Le la distribution gamma inverse
• Le distribution normale pli??e
• Le R??partition de la moiti?? de la normale
• Le distribution gaussienne inverse, aussi connue comme la distribution Wald
• Le Loi de L??vy
• Le la distribution log-logistique
• Le la distribution log-normale, d??crivant les variables qui peuvent ??tre mod??lis??es comme le produit de nombreuses petites variables positives ind??pendants.

Distribution de Pareto

• Le Distribution de Pareto, ou la distribution de "loi de puissance", utilis??e dans l'analyse des donn??es financi??res et comportement critique.
• La distribution de Pearson de type III (voir Distributions Pearson)
• Le Distribution de Rayleigh
• Le Distribution de Rayleigh m??lange
• Le Distribution de Rice
• Le Rosin Rammler de distribution - utilis?? pour d??crire le R??partition de la taille des particules de particules g??n??r??es par broyage, fraisage et op??rations de concassage.
• Le distribution de Gumbel type 2
• Le Distribution de Weibull, dont la distribution exponentielle est un cas particulier, est utilis?? pour mod??liser la dur??e de vie des dispositifs techniques.

Pris en charge sur toute la ligne r??elle

Distribution de Cauchy

La distribution de Laplace

La distribution Levy

Distribution normale

• Le Distribution de Cauchy, un exemple d'une distribution qui ne ont pas un valeur attendue ou d'une variance . En physique, il est g??n??ralement appel?? Profil de Lorentz, et est associ??e ?? de nombreux proc??d??s, y compris la distribution d'??nergie de r??sonance, l'impact et naturel ??largissement de la raie spectrale et quadratique Stark ??largissement de ligne.
• Le Fisher-Tippett, valeur extr??me, ou connectez-Weibull la distribution
  • Le Distribution de Gumbel, un cas particulier de la distribution de Fisher-Tippett
• Loi z de Fisher
• Le distribution des valeurs extr??mes g??n??ralis??e
• Le la distribution hyperbolique
• Le r??partition s??cante hyperbolique
• Le Loi de Landau
• Le La distribution de Laplace
• Le La distribution alpha-stable biais L??vy est souvent utilis?? pour caract??riser les donn??es financi??res et comportement critique.
• Le carte de distribution-Airy
• La distribution normale , aussi appel?? le Gauss ou la courbe en cloche. Il est omnipr??sent dans la nature et les statistiques en raison de la th??or??me central limite: chaque variable qui peut ??tre mod??lis??e comme une somme de nombreux petits variables ind??pendantes est ?? peu pr??s normale.
• Le Distribution de Pearson de type IV (voir Distributions Pearson)
• Loi de Student , utile pour estimer des moyens inconnus des populations gaussiennes.
  • Le distribution t non centrale
• Le distribution de Gumbel type 1
• Le R??partition Voigt, ou profil Voigt, est la convolution d'une distribution normale et une Distribution de Cauchy. On le trouve dans la spectroscopie lorsque les profils de raies spectrales sont ??largies par un m??lange de Lorentz et Doppler m??canismes ??largir.

Distributions conjointes

Pour tout ensemble de variables al??atoires ind??pendantes du fonction de densit?? de probabilit?? de leur distribution conjointe est le produit de leurs fonctions individuelles de densit??.

distributions Matrix-??valu??

• Distribution de Wishart
• distribution normale matrice
• matrice distribution t
• T-carr?? de la distribution de Hotelling