
Distribution binomiale
Saviez-vous ...
Ce contenu de Wikipedia a ??t?? s??lectionn?? par SOS Enfants d'aptitude dans les ??coles ?? travers le monde. Une bonne fa??on d'aider d'autres enfants est de parrainer un enfant
Fonction de masse  | |
Fonction de distribution cumulative  Couleurs correspondent ?? l'image ci-dessus | |
| Param??tres | 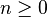 nombre d'essais ( entier ) nombre d'essais ( entier )  probabilit?? de succ??s ( r??el ) probabilit?? de succ??s ( r??el ) |
|---|---|
| Soutien |  |
| PMF |  |
| CDF |  |
| Signifier |  |
| M??diane | un des  |
| Mode |  |
| Variance |  |
| Asym??trie | 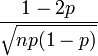 |
| Ex. aplatissement |  |
| Entropy |  |
| MGF |  |
| FC |  |
Dans la th??orie des probabilit??s et des statistiques , la distribution binomiale est la distribution de probabilit?? discr??te du nombre de succ??s dans une s??quence de n oui / non exp??riences ind??pendantes, dont chacune rendements succ??s avec probabilit?? p. Une telle / exp??rience de l'??chec de r??ussite est aussi appel?? une exp??rience de Bernoulli ou Essai de Bernoulli. En fait, lorsque n = 1, la distribution binomiale est un Distribution de Bernoulli. La distribution binomiale est la base de la populaire test binomial de signification statistique. Une distribution binomiale ne doit pas ??tre confondu avec un distribution bimodale.
Exemples
Un exemple ??l??mentaire est la suivante: Passer une norme mourir dix fois et compter le nombre de six. La distribution de ce nombre al??atoire est une distribution binomiale avec n = 10 et p = 1/6.
Comme autre exemple, supposons 5% d'une tr??s grande population d'??tre aux yeux verts. Vous choisissez 100 personnes au hasard. Le nombre de personnes aux yeux verts que vous choisissez est une variable al??atoire X qui suit une loi binomiale avec n = 100 et p = 0,05.
Sp??cification
Fonction de masse
En g??n??ral, si la variable al??atoire K suit la loi binomiale de param??tres n et p, nous ??crivons K ~ B (n, p). La probabilit?? d'obtenir exactement k succ??s dans les essais n est donn??e par la probabilit?? fonction de masse:
pour k = 0, 1, 2, ..., n et o??
est le coefficient binomial (d'o?? le nom de la distribution) "n choisir k" (??galement not??e C (n, k) ou n C k). La formule peut ??tre comprise comme suit: nous voulons k succ??s (p k) et n - k ??checs (1 - p) n - k. Toutefois, les succ??s k peuvent se produire ne importe o?? entre les n essais, et il n'y a C (n, k) diff??rentes fa??ons de distribuer k succ??s dans une s??quence de n essais.
Dans la cr??ation de tables de r??f??rence pour probabilit?? de distribution binomiale, habituellement le tableau est rempli jusqu'?? n / 2 valeurs. En effet, pour k> n / 2, la probabilit?? peut ??tre calcul??e en tant que son compl??ment
Donc, il faut regarder ?? un k diff??rent et une autre p (le bin??me ne est pas sym??trique en g??n??ral).
Fonction de distribution cumulative
Le fonction de distribution cumulative peut ??tre exprim??e en termes de la r??gularis?? fonction b??ta incompl??te, comme suit:
?? condition que k est un entier et 0 ≤ k ≤ n. Si x ne est pas n??cessairement un nombre entier ou pas n??cessairement positif, on peut se exprimer ainsi:
Pour k ≤ np, les limites sup??rieures de la queue inf??rieure de la fonction de distribution peuvent ??tre d??riv??es. En particulier, In??galit?? de Hoeffding donne la borne
et In??galit?? de Chernoff peut ??tre utilis??e pour d??river la limite
Moyenne, la variance et le mode
Si X ~ B (n, p) (ce est-?? X est une variable al??atoire binomiale distribu??), le valeur attendue de X est
et la variance est
Ce fait est facilement prouv?? comme suit. Supposons d'abord que nous avons exactement un essai de Bernoulli. Nous avons deux r??sultats possibles, 1 et 0, le premier ayant probabilit?? p et la seconde ayant une probabilit?? - p; la moyenne pour cet essai est donn??e par μ = p. En utilisant la d??finition de la variance , on a
Maintenant supposons que nous voulons que la variance pour ces essais n (ce est ?? dire pour la loi binomiale g??n??ral). Depuis les essais sont ind??pendants, on peut ajouter les ??carts pour chaque essai, donnant
Le Mode de X est le plus grand entier inf??rieur ou ??gal ?? (n + 1) p; si m = (n + 1) p est un nombre entier, alors m - 1 et m sont les deux modes.
D??rivations explicites de moyenne et la variance
Nous d??rivons ces quantit??s ?? partir des premiers principes. Certaines sommes particuliers se produisent dans ces deux d??rivations. Nous r??organisons les sommes et les conditions afin que r??sume uniquement sur les fonctions de masse de probabilit?? binomiale complets ( PMF ) se pose, qui sont toujours l'unit??
Signifier
Nous appliquons la d??finition de la valeur attendue d'une variable al??atoire discr??te ?? la distribution binomiale
Le premier terme de la s??rie (d'indice k = 0) a la valeur 0 puisque le premier facteur, k, est nul. Il peut donc ??tre ??cart??e, ce est ?? dire que nous pouvons changer la limite inf??rieure ??: k = 1
Nous avons tir?? de facteurs n et k sur les factorielles, et une puissance de P a ??t?? scind??. Nous nous pr??parons ?? red??finir les indices.
Nous renommer m = n - 1 et s = k - 1. La valeur de la somme ne est pas modifi?? par cela, mais il devient d??sormais facilement identifiables
La somme qui a suivi est une somme sur un bin??me compl??te pmf (d'un ordre inf??rieur ?? la somme initiale, en l'occurrence). Ainsi
Variance
On peut montrer que la variance est ??gale ?? (voir: la variance, 10. formule de calcul de la variance ):
En utilisant cette formule, nous voyons que nous avons maintenant besoin de la valeur attendue de X 2, qui est
Nous pouvons utiliser notre exp??rience acquise ci-dessus en d??rivant la moyenne. Nous savons comment traiter une facteur k. Cela nous arrive aussi loin que
(?? nouveau, avec m = n - 1 et s = k - 1). Nous avons divis?? la somme en deux sommes s??par??s et nous reconnaissons chacun
La premi??re somme est identique dans la forme ?? celle nous avons calcul?? dans la moyenne (ci-dessus). Il r??sume ?? point de fusion. La deuxi??me somme est l'unit??.
En utilisant ce r??sultat dans l'expression de la variance, avec le moyen (E (X) = np), nous obtenons
Relations avec d'autres distributions
Sommes des bin??mes
Si X ~ B (n, p) et Y ~ B (m, p) sont des variables binomiales ind??pendantes, alors x + y est de nouveau une variable binomiale; sa distribution est
Approximation normale

Si n est suffisamment grand, la dissym??trie de la distribution ne est pas trop grande, et une appropri?? correction de continuit?? est utilis??, une excellente approximation ?? B (n, p) est donn??e par la distribution normale
Divers r??gles empiriques peuvent ??tre utilis??s pour d??cider si n est assez grand. Une r??gle est que les deux np et n (1 - p) doit ??tre sup??rieur ?? 5. Toutefois, le nombre pr??cis varie d'une source ??, et d??pend de comment bon une approximation on veut; certaines sources donnent 10. Une autre r??gle couramment utilis?? soutient que l'approximation normale ci-dessus est appropri??e que si
Ce qui suit est un exemple de l'application d'un correction de continuit??: Supposons que l'on souhaite calculer Pr (X ≤ 8) pour un bin??me variable al??atoire X. Si Y a une distribution donn??e par l'approximation normale, puis Pr (X ≤ 8) est approch??e par le Pr (Y ≤ 8,5). L'addition de 0,5 est la correction de continuit??; l'approximation normale non corrig??e donne des r??sultats beaucoup moins pr??cises.
Cette approximation est un gain de temps ??norme (des calculs exacts avec grande n sont tr??s on??reux); Historiquement, ce est la premi??re utilisation de la distribution normale, introduit en Le livre d'Abraham de Moivre La th??orie des probabilit??s en 1733. Aujourd'hui, elle peut ??tre consid??r??e comme une cons??quence de la th??or??me central limite puisque B (n, p) est une somme de n ind??pendant, identiquement distribu??es 0-1 variables indicatrices.
Par exemple, supposons que vous go??ter au hasard n personnes sur une population nombreuse et leur demander se ils sont d'accord avec un certain d??claration. La proportion de personnes qui acceptent d??pendra bien s??r sur l'??chantillon. Si vous avez ??chantillonn?? groupes de n personnes ?? plusieurs reprises et v??ritablement au hasard, les proportions souhaitez suivre une distribution normale avec une moyenne approximative ??gale ?? la proportion vraie p d'accord dans la population et avec un ??cart type σ = (p (1 - p) n) 1 / 2. Grand taille de l'??chantillon n sont bonnes parce que l'??cart-type, en proportion de la valeur attendue, devient plus petit, ce qui permet une estimation plus pr??cise du param??tre inconnu p.
Approximation de Poisson
La distribution binomiale converge vers la distribution de Poisson comme le nombre d'essais tend vers l'infini tandis que le produit np reste fixe. Par cons??quent, la loi de Poisson de param??tre λ = np peut ??tre utilis??e comme une approximation de B (n, p) de la distribution binomiale si n est suffisamment grand et p est suffisamment faible. Selon deux r??gles de base, cette approximation est bonne si n ≥ 20 et p ≤ 0,05, ou si n ≥ 100 et ≤ 10 np.
Limites de la distribution binomiale
- Comme n tend vers ∞ et p se approche de 0 alors np reste fix?? ?? λ> 0 ou au moins np approche λ> 0, alors le binomiale (n, p) la distribution se rapproche de la distribution de Poisson avec λ de valeur attendue.
- Lorsque n tend vers ∞ p reste fixe alors que, la r??partition des
- se rapproche de la distribution normale avec la valeur attendue 0 et variance 1 (ce est juste un cas sp??cifique de la Th??or??me central limite).


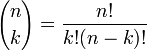




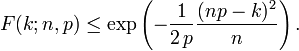


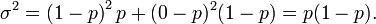
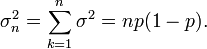


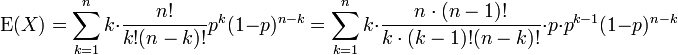

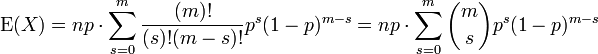






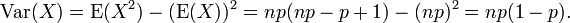
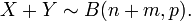

![\ Mu h \ 3 \ sigma = np \ h 3 \ sqrt {np (1-p)} \ in [0, n].](../../images/195/19591.png)

