Distribution de Poisson

?? propos de ce ??coles s??lection Wikipedia

SOS Enfants, un organisme de bienfaisance de l'??ducation , a organis?? cette s??lection. Voir http://www.soschildren.org/sponsor-a-child pour conna??tre le parrainage d'enfants.

Poisson
Fonction de masse L'axe horizontal est l'indice k. La fonction est d??finie seulement ?? des valeurs enti??res de k. Les lignes de connexion ne sont que des guides pour l'??il et ne indiquent pas la continuit??.
Fonction de distribution cumulative L'axe horizontal est l'indice k.
Param??tres	$\ Lambda \ dans (0, \ infty)$
Soutien	$k \ in \ {0,1,2, \ ldots \}$
PMF	$\ Frac {e ^ {- \ lambda} \ lambda ^ k} {k!} \!$
CDF	$\ Frac {\ Gamma (\ lfloor k + 1 \ rfloor, \ lambda)} {\ lfloor k \ rfloor!} \! \ Text {for} k \ ge 0$ (O?? $\ Gamma (x, y)$ est le Fonction gamma incompl??te)
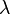Signifier	$\ Lambda \,$
M??diane	$\ Text {habituellement environ} \ lfloor \ lambda + 1/3 ?? 0,02 / \ lambda \ rfloor$
Mode	$\ Lfloor \ lambda \ rfloor$ et $\ Lambda-1$ si $\ Lambda$ est un nombre entier
Variance	$\ Lambda \,$
Asym??trie	$\ Lambda ^ {- 1/2} \,$
Ex. aplatissement	$\ Lambda ^ {- 1} \,$
Entropy	$\ Lambda [1 \ -! \ \ Ln (\ lambda)]! \ + \ E ^ {- \ lambda} \ sum_ {k = 0} ^ \ infty \ frac {\ lambda ^ k \ ln (k! )} {k!}$ (Pour les grands $\ Lambda$ ) $\ Frac {1} {2} \ log (2 \ pi e \ lambda) - \ frac {1} {12 \ lambda} - \ frac {1} {24 \ lambda ^ 2} - \ frac {19} {360 \ lambda ^ 3} + O (\ frac {1} {\ lambda ^ 4})$
MGF	$\ Exp (\ lambda (e ^ t-1)) \,$
FC	$\ Exp (\ lambda (e ^ {it} -1)) \,$

Dans la th??orie des probabilit??s et des statistiques , la distribution de Poisson est une distribution de probabilit?? discr??te qui exprime la probabilit?? d'un certain nombre d'??v??nements qui se produisent dans une p??riode de temps d??termin??e si ces ??v??nements se produisent avec un taux moyen connu et ind??pendamment du temps ??coul?? depuis le dernier ??v??nement. La distribution de Poisson peut ??galement ??tre utilis?? pour le nombre d'??v??nements dans d'autres intervalles d??termin??s tels que la distance, surface ou de volume.

La distribution a ??t?? d??couvert par Sim??on-Denis Poisson ( 1781 - 1840 ) et publi??e, avec sa th??orie de la probabilit??, en 1838 dans son ouvrage Recherches sur la Probabilit?? des Jugements en mati??res criminelles et mati??re civile (??La recherche sur la probabilit?? des d??cisions en mati??re civile et p??nale??) . Les travaux ont port?? sur certaines variables al??atoires N qui comptent, entre autres, un certain nombre d'occurrences discr??tes (parfois appel?? ??arriv??es??) qui ont lieu au cours d'un temps -interval de longueur donn??e. Si le nombre d'occurrences pr??vu dans cet intervalle est λ, alors la probabilit?? que sont exactement les occurrences k (k ??tant un non-n??gatif entier , k = 0, 1, 2, ...) est ??gal ??

$f (k, \ lambda) = \ frac {\ lambda ^ ke ^ {- \ lambda}} {k!}, \, \!$

o??

e est la base du logarithme naturel (e = 2,71828 ...)
k est le nombre d'occurrences d'un ??v??nement - dont la probabilit?? est donn??e par la fonction
k! est la factorielle de k
λ est positif un nombre r??el ??gal au nombre attendu d'??v??nements qui se produisent pendant l'intervalle donn??. Par exemple, si les ??v??nements se produisent en moyenne toutes les 4 minutes, et vous ??tes int??ress?? par le nombre d'??v??nements survenus dans un intervalle de 10 minutes, vous pouvez utiliser comme mod??le une distribution de Poisson avec λ = 10/4 = 2,5.

En fonction de k, ce est le Fonction de masse. La distribution de Poisson peut ??tre calcul??e comme un cas limite de la loi binomiale .

La distribution de Poisson peut ??tre appliqu??e ?? des syst??mes avec un grand nombre d'??v??nements possibles, dont chacun est rare. Un exemple classique est la d??sint??gration nucl??aire d'atomes.

La distribution de Poisson est parfois appel?? un de Poisson, analogue ?? la gaussienne terme de Gauss ou distribution normale .

bruit de Poisson et la caract??risation de petites occurrences

Le param??tre λ est pas seulement le moyen pour nombre d'occurrences $\ Scriptstyle \ langle k \ rangle$ , Mais aussi sa variance $\ Scriptstyle \ sigma_k ^ 2 \ \ stackrel {\ mathrm {def}} {} = \ \ langle k ^ {2} \ rangle - \ langle k \ rangle ^ {2}$ (Voir le tableau). Ainsi, le nombre d'occurrences observ??es fluctue autour de sa moyenne λ avec un ??cart-type $\ Scriptstyle \ sigma_ {k} \, = \, \ sqrt {\ lambda}$ . Ces fluctuations sont d??sign??s par le bruit de Poisson ou (en particulier dans l'??lectronique) que bruit de grenaille.

La corr??lation de l'??cart moyen et l'??cart dans le comptage, les ??v??nements discrets ind??pendants est utile scientifiquement. En surveillant la fa??on dont les fluctuations varient avec le signal de moyenne, on peut estimer la contribution d'un seul ??v??nement, m??me si cette contribution ne est trop petit pour ??tre d??tect?? directement. Par exemple, la charge e sur un ??lectron peut ??tre estim?? en corr??lant l'amplitude d'un courant ??lectrique avec son bruit de grenaille. Si N ??lectrons passent un point dans un temps donn?? t en moyenne, la moyenne courant est I = fr / t; puisque les fluctuations actuelles devraient ??tre de l'ordre $\ Scriptstyle \ sigma_ {I} = e \ sqrt {N / t \}$ (Ce est ?? dire l' ??cart du processus de Poisson), la charge e peut ??tre estim??e ?? partir du rapport $\ Scriptstyle \ sigma_ {I} ^ {2} / I$ . Un exemple courant est le grain qui appara??t comme des photos sont agrandies; le grain est en raison des fluctuations de Poisson du nombre de r??duction argent c??r??ales, de ne pas les grains individuels eux-m??mes. En corr??lant le grain avec le degr?? de l'??largissement, on peut estimer la contribution d'un grain individuel (qui est par ailleurs trop petit pour ??tre vu nu). De nombreuses autres applications mol??culaires de Poisson bruit ont ??t?? d??velopp??s, par exemple, l'estimation de la densit?? en nombre de des mol??cules de r??cepteur dans un membrane cellulaire.

$\ Pr (N_t = k) = f (k; \ lambda t) = \ frac {e ^ {- \ lambda t} (\ lambda t) ^ k} {k!}, \, \!$

Distributions connexes

Si $X_1 \ sim \ mathrm {} Pois (\ lambda_1) \,$ et $X_2 \ sim \ mathrm {} Pois (\ lambda_2) \,$ alors la diff??rence $Y = X_1 - X_2$ suit une Loi de Skellam.
Si $X_1 \ sim \ mathrm {} Pois (\ lambda_1) \,$ et $X_2 \ sim \ mathrm {} Pois (\ lambda_2) \,$ sont ind??pendants, et $Y = X_1 + X_2$ , Alors la distribution de $X_1$ sur conditionnelle $Y = y$ est un bin??me . Plus pr??cis??ment, $X_1 | (Y = y) \ sim \ mathrm {} Binom (y, \ lambda_1 / (\ + lambda_1 \ lambda_2)) \,$ . Plus g??n??ralement, si X _1, X _2, ..., X _n sont des variables al??atoires de Poisson avec des param??tres λ _1, λ _2, ..., λ _n, puis $X_i \ left | \ sum_ {j = 1} ^ n x_j \ right. \ Sim \ mathrm {Binom} \ left (\ sum_ {j = 1} ^ nX_j, \ frac {\ lambda_i} {\ sum_ {j = 1} ^ n \ lambda_j} \ right)$
La distribution de Poisson peut ??tre d??riv?? comme un cas limite de la distribution binomiale en tant que le nombre d'essais tend vers l'infini et le nombre pr??vu de succ??s reste fixe. Par cons??quent, il peut ??tre utilis?? comme une approximation de la distribution binomiale si n est suffisamment grand et p est suffisamment faible. Il existe une r??gle de base indiquant que la distribution de Poisson est une bonne approximation de la distribution binomiale si n vaut au moins 20 et p est inf??rieur ou ??gal ?? 0,05. Selon cette r??gle, le rapprochement est excellent si n ≥ 100 et ≤ 10 np.
Pour suffisamment grandes valeurs de λ, (par exemple λ> 1 000), la distribution normale avec la moyenne λ, λ et la variance, est une excellente approximation de la distribution de Poisson. Si λ est sup??rieur ?? environ 10, puis la distribution normale est une bonne approximation si une appropri??e correction de continuit?? est r??alis??, ce est ?? dire P (X ≤ x), o?? (minuscules) x est un nombre entier non-n??gatif, est remplac?? par P (X ≤ x + 0,5).

$F_ \ mathrm {} Poisson (x; \ lambda) \ approx F_ \ mathrm {} normale (x; \ mu = \ lambda, \ sigma ^ 2 = \ lambda) \,$

Si le nombre d'arriv??es dans un temps donn?? suite ?? la distribution de Poisson, de moyenne = 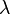$\ Lambda$ , Alors les longueurs des temps inter-arriv??es suivent la Distribution exponentielle , avec un taux $1 / \ lambda$ .

Occurrence

La distribution de Poisson se pose dans le cadre de Processus de Poisson. Elle se applique aux divers ph??nom??nes de nature discr??te (ce est ?? dire ceux qui peuvent se produire ?? 0, 1, 2, 3, ... fois pendant une p??riode de temps donn??e ou dans une zone donn??e) chaque fois que la probabilit?? de ce ph??nom??ne se produit est constant dans temps ou espace. Des exemples d'??v??nements qui peuvent ??tre mod??lis??es comme une distribution de Poisson comprennent:

Le nombre de voitures qui passent ?? travers un certain point sur une route (?? une distance suffisante de feux de circulation) pendant une p??riode de temps donn??e.
Le nombre de fautes d'orthographe lors de la frappe on fait une seule page.
Le nombre de coups de t??l??phone ?? un centre d'appel par minute.
Le nombre de fois qu'un serveur Web est accessible par minute.
Le nombre de Roadkill (animaux tu??s) trouv?? par unit?? de longueur de la route.
Le nombre de des mutations dans un segment donn?? de l'ADN apr??s une certaine quantit?? de rayonnement.
Le nombre de instables noyaux decay?? que dans une p??riode de temps donn??e dans un morceau de substance radioactive. La radioactivit?? de la substance se affaiblissent avec le temps, si l'intervalle de temps total utilis?? dans le mod??le doit ??tre nettement inf??rieure ?? la dur??e de vie de la substance signifie.
Le nombre d'arbres de pin par unit?? de surface de for??t mixte.
Le nombre de ??toiles dans un volume donn?? de l'espace.
Le nombre de soldats tu??s par des coups de pied de chevaux chaque ann??e dans chaque corps de la Cavalerie prussienne. Cet exemple a ??t?? rendu c??l??bre par un livre de Ladislaus Bortkiewicz Josephovich ( 1868 - 1931 ).
La distribution des cellules des r??cepteurs visuels de la r??tine de la humaine oeil .
Le nombre d'ampoules qui grillent en un certain laps de temps.
Le nombre de virus qui peuvent infecter une cellule en culture cellulaire.
Le nombre de cellules souches h??matopo????tiques dans un ??chantillon de cellules de moelle osseuse non fractionn??e.
Le nombre d'inventions d'un inventeur cours de leur carri??re.
Le nombre de particules qui "scatter" hors d'une cible dans une exp??rience de physique nucl??aire ou ??lev??.

[Note: les intervalles entre les ??v??nements successifs de Poisson sont-li??s r??ciproquement, la suite de la Distribution exponentielle . Par exemple, la dur??e de vie d'une ampoule, ou le temps d'attente entre les bus.]

Comment cette distribution se pose? - La loi d'??v??nements rares

Dans plusieurs de l'exemple des exemples-ci-dessus, le nombre de mutations dans une s??quence donn??e d'ADN les ??v??nements ??tant compt??s sont en fait les r??sultats des essais discrets, et serait plus pr??cis??ment ??tre mod??lis??e en utilisant la loi binomiale . Cependant, la distribution binomiale de param??tres n et λ / n, ce est ?? dire, la distribution de probabilit?? du nombre de succ??s en n essais, avec une probabilit?? λ / n de r??ussite ?? chaque essai, se rapproche de la distribution de Poisson avec une valeur attendue λ que n tend vers l'infini . Cette limite est parfois connu comme la loi d'??v??nements rares, bien que ce nom peut ??tre trompeur parce que les ??v??nements dans un processus de Poisson ne sont pas n??cessairement rares (le nombre d'appels t??l??phoniques ?? un standard tr??s occup?? en une heure suit une distribution de Poisson, mais ces ??v??nements ne serait pas consid??r??e comme rare). Il fournit un moyen par lequel, rapprochant les variables al??atoires en utilisant la distribution de Poisson, plut??t que la distribution binomiale plus encombrant.

Voici les d??tails. Tout d'abord, rappeler de calcul que

$\ Lim_ {n \ to \ infty} \ left (1 - {\ lambda \ over n} \ right) ^ n = e ^ {- \ lambda}.$

Soit p = λ / n. Ensuite, nous avons

$\ Lim_ {n \ to \ infty} \ Pr (X = k) = \ lim_ {n \ to \ infty} {n \ choisir k} p ^ k (1-p) ^ {nk} = \ lim_ {n \ ?? \ infty} {n! ! \ Over (nk) k} \ left ({\ lambda \ over n} \ right) ^ k \ left (1 - {\ lambda \ over n} \ right) ^ {nk}$

$= \ Lim_ {n \ to \ infty} \ underbrace {\ left ({n \ over n} \ right) \ gauche ({n-1 \ over n} \ right) \ gauche ({n-2 \ over n} \ right) \ cdots \ gauche ({n-k + 1 \ over n} \ right)} \ \ underbrace {\ left ({\ lambda ^ k \ over k!} \ right)} \ \ underbrace {\ left ( 1 - {\ lambda \ over n} \ right) ^ n} \ \ underbrace {\ left (1 - {\ lambda \ over n} \ right) ^ {- k}}$

Comme n tend vers ∞, l'expression sur le premier underbrace approche 1; le second reste constant depuis "n" ne appara??t pas dans du tout; la troisi??me approche e ^-λ; et la quatri??me expression approche 1.

Par cons??quent, la limite est

${\ Lambda ^ k e ^ {- \ lambda} \ over k!} \, \.!$

Plus g??n??ralement, chaque fois une s??quence de variables al??atoires binomiale de param??tres n et p _n est telle que

$\ Lim_ {n \ rightarrow \ infty} np_n = \ lambda,$

la s??quence converge en loi vers une variable al??atoire de Poisson de moyenne λ (voir, par exemple, la loi d'??v??nements rares).

Propri??t??s

Le valeur attendue d'une variable al??atoire de Poisson-distribu??e est ??gale ?? λ et il en est de sa variance . La plus haute des moments de la distribution de Poisson sont Polyn??mes Touchard ?? λ, dont les coefficients ont une combinatoire sens. En fait, lorsque la valeur attendue de la distribution de Poisson est 1, alors La formule de Dobinski dit que le n-i??me instant ??gal au nombre de partitions d'un ensemble de taille n.

Le Mode d'une variable al??atoire de Poisson-distribu?? avec non entier λ est ??gal ?? $\ Scriptstyle \ lfloor \ lambda \ rfloor$ , Qui est le plus grand entier inf??rieur ou ??gal ?? λ. Ce est aussi ??crit que ??tage (λ). Lorsque λ est un nombre entier positif, les modes sont λ et λ - 1.

Les sommes de variables al??atoires de Poisson distribu??s:

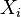Si $X_i \ sim \ mathrm {} Poi (\ lambda_i) \,$ suivre une distribution de Poisson de param??tre $\ Lambda_i \,$ et $X_i$ sont ind??pendante, puis $Y = \ sum_ {i = 1} ^ N X_i \ sim \ mathrm {Poi} \ left (\ sum_ {i = 1} ^ N \ lambda_i \ right) \,$ suit aussi une loi de Poisson dont le param??tre est la somme des param??tres de composants.

Le Fonction g??n??ratrice des moments de la distribution de Poisson avec une valeur λ est attendue

$\ Mathrm {E} \ left (e ^ {tX} \ right) = \ sum_ {k = 0} ^ \ infty e ^ {tk} f (k; \ lambda) = \ sum_ {k = 0} ^ \ infty e ^ {tk} {\ lambda ^ ke ^ {- \ lambda} \ over k} = e ^ {\ lambda (e ^ t-1)}.$

La totalit?? de la cumulants de la distribution de Poisson sont ??gales ?? la valeur λ attendu. La n-i??me moment factoriel de la distribution de Poisson est λ ^n.

Les distributions de Poisson sont infiniment divisible distributions de probabilit??.

La sc??ne Kullback-Leibler entre Poi (λ ₀₎ et Poi (λ) est donn??e par

$\ Delta (\ lambda || \ lambda_0) = \ lambda \ left (1 - \ frac {\ lambda_0} {\ lambda} + \ frac {\ lambda_0} {\ lambda} \ log \ frac {\ lambda_0} {\ lambda } \ right).$

G??n??ration Poisson-distribu?? variables al??atoires

Une fa??on simple de g??n??rer des num??ros de Poisson-distribu??s au hasard est donn??e par Knuth , voir les r??f??rences ci-dessous.

 algorithme poisson nombre al??atoire (Knuth):
     INIT:
          Soit L ← e ^-λ, k ← ← p 0 et 1.
     faire:
          k ← k + 1.
          G??n??rer uniforme nombre al??atoire u dans [0,1] et laisser p ← p ?? u.
     tout p ≥ L.
     retourner k - 1.

Bien que simple, la complexit?? est lin??aire en λ. Il ya beaucoup d'autres algorithmes pour surmonter cela. Certains sont donn??s dans Ahrens & Dieter, voir les r??f??rences ci-dessous.

Estimation des param??tres

Maximum de vraisemblance

??tant donn?? un ??chantillon de n valeurs mesur??es k _i nous voulons estimer la valeur du param??tre λ de la population de Poisson ?? partir de laquelle l'??chantillon a ??t?? tir??. Pour calculer le la valeur du maximum de vraisemblance, nous formons la fonction log-vraisemblance

$L (\ lambda) = \ ln \ prod_ {i = 1} ^ nf (K_i \ mi \ lambda) \!$

$= \ Sum_ {i = 1} ^ n \ ln \ \ left (\ frac {e ^ {- \ lambda} \ lambda ^ {}} {K_i K_i!} \ Right)! \!$

$= -n \ Lambda + \ left (\ sum_ {i = 1} ^ n K_i \ right) \ ln (\ lambda) - \ sum_ {i = 1} ^ n \ ln (K_i!). \!$

Prenez la d??riv??e de L par rapport ?? λ et l'assimiler ?? z??ro:

$\ Frac {\ mathrm {d}} {\ mathrm {d} \ lambda} L (\ lambda) = 0 \ ssi -n + \ left (\ sum_ {i = 1} ^ n K_i \ right) \ frac {1 } {\ lambda} = 0 \!$

La r??solution de λ donne l'estimation du maximum de vraisemblance de λ:

$\ Widehat {\ lambda} _ \ mathrm {} MLE = \ frac {1} {n} \ sum_ {i = 1} ^ n K_i. \!$

Depuis chaque observation a attente λ donc cela moyenne de l'??chantillon. Ce est donc un estimateur sans biais de λ. Ce est ??galement un estimateur efficace, ce est ?? dire sa variance d'estimation permet d'obtenir la Cram??r-Rao (BCR).

Inf??rence bay??sienne

Dans l'inf??rence bay??sienne , la Conjugu?? avant pour le param??tre de taux λ de la distribution de Poisson est le Distribution Gamma. Laisser

$\ Lambda \ sim \ mathrm {Gamma} (\ alpha, \ beta) \!$

indiquer que λ est distribu?? selon le Gamma densit?? g param??tr??e en termes de fa??onner param??tre α et un inverse param??tre d'??chelle β:

$g (\ lambda \ mi \ alpha, \ beta) = \ frac {\ beta ^ {\ alpha}} {\ Gamma (\ alpha)} \; \ Lambda ^ {\ alpha-1} \; e ^ {- \ beta \, \ lambda} \ qquad \ mbox {for} \ \ lambda> 0 \, \ !.$

Ensuite, ??tant donn?? le m??me ??chantillon de n valeurs k _i mesur??s comme pr??c??demment, et un avant de Gamma (α, β), la distribution post??rieure est

$\ Lambda \ sim \ mathrm {Gamma} (\ alpha + \ sum_ {i = 1} ^ n K_i, \ frac {1} {\ frac {1} {\ beta}} + n). \!$

La moyenne a posteriori E [λ] se rapproche l'estimation du maximum de vraisemblance $\ Widehat {\ lambda} _ \ mathrm {} MLE$ dans la limite que $\ Alpha \ 0, \ \ beta \ 0$ .

La distribution pr??dictive post??rieure des donn??es suppl??mentaire est un Gamma-Poisson (c. binomiale) distribution n??gative.

La ??loi des petits nombres"

La loi de mot est parfois utilis?? comme synonyme de distribution de probabilit?? , et la convergence en droit signifie la convergence dans la distribution. En cons??quence, la distribution de Poisson est parfois appel??e la loi des petits nombres parce que ce est la distribution de probabilit?? du nombre d'occurrences d'un ??v??nement qui se produit rarement, mais a de tr??s nombreuses occasions de se produire. La loi des petits nombres est un livre ??crit par Ladislaus Bortkiewicz sur la distribution de Poisson, publi?? en 1898 . Certains historiens des math??matiques ont fait valoir que la distribution de Poisson aurait d?? se appeler la distribution Bortkiewicz.

Calculer une approximation de la probabilit?? de Poisson

Lorsque k devient grand (> 20) l'utilisation des journaux et des approximations factorielles sont n??cessaires. Voici un exemple ??crit en Java.

 / ** Calcule une approximation de la probabilit?? de Poisson.  *param Moyenne - lambda, le nombre moyen d'occurrences *param observ?? - le nombre r??el d'occurrences observ??es *return ln (probabilit?? de Poisson) - le logarithme naturel de la probabilit?? de Poisson. */ public static double poissonProbabilityApproximation ( double mean, int observed ) { double k = observed ; double a = k * Math . log ( mean ) ; double b = - mean ; return a + b - factorialApproximation ( k ) ; } /**Srinivasa  Ramanujan ln (n!) D'estimation factorielle.  * Bon pour les plus grandes valeurs de n.  *return Ln (n!) */ public static double factorialApproximation ( double n ) { if ( n < 2 . ) return 0 ; double a = n * Math . log ( n ) - n ; double b = Math . log ( n * ( 1 . + 4 . * n * ( 1 . + 2 . * n ) ) ) / 6 . ; return a + b + Math . log ( Math . PI ) / 2 . ; }

Outils de visualisation en ligne

SOCR R??partition GUI
Interactive Poisson R??partition de TAMU

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Poisson_distribution&oldid=197206369 "