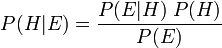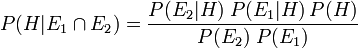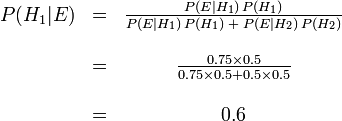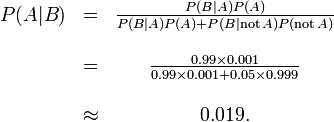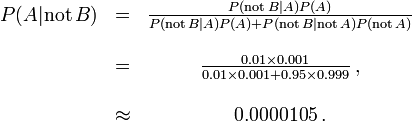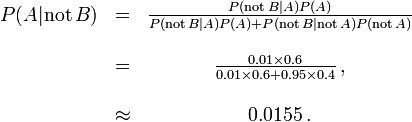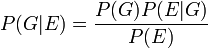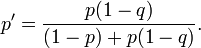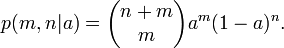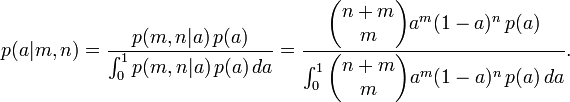Inf??rence bay??sienne

?? propos de ce ??coles s??lection Wikipedia

Cette s??lection ??coles a ??t?? choisi par SOS Enfants pour les ??coles dans le monde en d??veloppement ne ont pas acc??s ?? Internet. Il est disponible en t??l??chargement intranet. Un lien rapide pour le parrainage d'enfants est http://www.sponsor-a-child.org.uk/

Inf??rence bay??sienne est inf??rence statistique dans lequel des preuves ou des observations sont utilis??s pour mettre ?? jour ou nouvellement d??duire la probabilit?? qu'une hypoth??se peut ??tre vrai. Le nom "bay??sien" vient de l'utilisation fr??quente de Le th??or??me de Bayes dans le processus d'inf??rence. Le th??or??me de Bayes a ??t?? d??riv?? du travail du r??v??rend Thomas Bayes.

Preuves et changer les croyances

L'inf??rence bay??sienne utilise les aspects de la m??thode scientifique, qui implique la collecte preuve qui est cens?? ??tre compatible ou incompatible avec une donn??e hypoth??se. Comme preuve se accumule, le degr?? de croyance en une hypoth??se doit changer. Avec suffisamment de preuves, il devrait devenir tr??s ??lev?? ou tr??s faible. Ainsi, les partisans de l'inf??rence bay??sienne disent qu'il peut ??tre utilis?? pour discriminer entre les hypoth??ses contradictoires: hypoth??ses ?? tr??s haute soutien devraient ??tre accept??es comme vraies et ceux qui ont tr??s peu de soutien devraient ??tre rejet??s comme faux. Cependant, les d??tracteurs disent que cette m??thode d'inf??rence peut ??tre biais??e en raison de croyances initiales que l'on doit tenir avant que la preuve ne est jamais recueillies.

Inf??rence bay??sienne utilise une estimation num??rique du degr?? de croyance en une hypoth??se avant que la preuve a ??t?? observ?? et calcule une estimation chiffr??e du degr?? de croyance dans l'hypoth??se apr??s que la preuve a ??t?? observ??. Inf??rence bay??sienne repose g??n??ralement sur degr??s de croyance, ou probabilit??s subjectives, dans le processus d'induction et ne pr??tend pas n??cessairement de fournir une m??thode objective de l'induction. N??anmoins, certains statisticiens bay??siens croire probabilit??s peuvent avoir une valeur objective et donc inf??rence bay??sienne peut fournir une m??thode objective de l'induction. Voir m??thode scientifique.

Le th??or??me de Bayes ajuste probabilit??s donn??es nouvelles preuves de la fa??on suivante:

$P (H | E) = \ frac {P (E | H) \; P (H)} {P (E)}$

o??

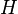$H$ repr??sente une hypoth??se sp??cifique, qui peuvent ou peuvent ne pas ??tre quelque hypoth??se nulle.
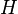$P (H)$ est appel?? le de probabilit?? a priori $H$ qui a ??t?? d??duit avant de nouvelles preuves, 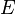$E$ , Est devenu disponible.
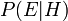$P (E | H)$ est appel?? le probabilit?? conditionnelle de voir la preuve 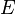$E$ si l'hypoth??se 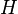$H$ passe pour ??tre vrai. Il est aussi appel?? un fonction de vraisemblance lorsque l'on consid??re comme une fonction de 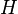$H$ pour fixe $E$ .
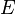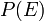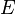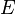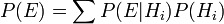$P (E)$ est appel?? le de probabilit?? marginale $E$ : La probabilit?? a priori d'??tre t??moin de la nouvelle preuve $E$ sous toutes les hypoth??ses possibles. Il peut ??tre calcul?? comme la somme du produit de toutes les probabilit??s de ne importe quel ensemble complet d'hypoth??ses mutuellement exclusives et probabilit??s conditionnelles correspondantes: $P (E) = \ sum P (E | h_i) P (h_i)$ .
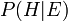$P (H | E)$ est appel?? le probabilit?? post??rieure de 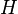$H$ donn?? $E$ .

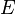Le facteur 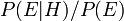$P (E | M) / P (E)$ repr??sente l'incidence que la preuve a sur la croyance dans l'hypoth??se. Se il est probable que la preuve 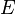$E$ serait observ??e lorsque l'hypoth??se ?? l'??tude est vrai, mais peu probable que 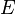$E$ aurait ??t?? le r??sultat de l'observation, ce facteur sera grand. La multiplication de la probabilit?? a priori de l'hypoth??se par ce facteur se traduirait par une plus grande probabilit?? a posteriori de l'hypoth??se ??tant donn?? la preuve. Inversement, se il est peu probable que la preuve 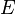$E$ serait observ??e si l'hypoth??se ?? l'??tude est vrai, mais a priori probable que 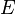$E$ serait observ??e, le facteur r??duirait la probabilit?? a posteriori pour $H$ . Sous l'inf??rence bay??sienne, le th??or??me de Bayes mesure donc combien de nouveaux ??l??ments de preuve devrait modifier une croyance en une hypoth??se.

Statisticiens bay??siens soutiennent que m??me lorsque les gens sont tr??s diff??rentes probabilit??s subjectives ant??rieures, de nouvelles preuves ?? partir d'observations r??p??t??es aura tendance ?? apporter leurs post??rieurs probabilit??s subjectives rapprocher. Cependant, d'autres soutiennent que lorsque les gens tiennent largement diff??rente subjective avant leurs probabilit??s post??rieures probabilit??s subjectives ne peuvent jamais converger m??me avec la collecte r??p??t??e de preuves. Ces critiques font valoir que les visions du monde qui sont compl??tement diff??rentes d'abord peuvent rester compl??tement diff??rente au fil du temps malgr?? une forte accumulation de preuves.

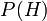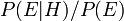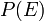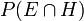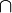Multipliant la probabilit?? a priori $P (H)$ par le facteur $P (E | M) / P (E)$ ne sera jamais donn?? une probabilit?? qui est sup??rieure ?? 1, ??tant donn?? que $P (E)$ est au moins aussi grande que $P (E \ cap H)$ (O?? $\ Cap$ d??signe "et"), ce qui ??quivaut ?? 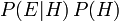$P (E | H) \, P (H)$ (Voir probabilit?? conjointe).

La probabilit?? de 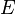$E$ donn?? 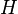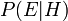$H$ , $P (E | H)$ , Peut ??tre repr??sent?? comme une fonction de son second argument avec son premier argument maintenu fixe. Une telle fonction est appel??e fonction de vraisemblance; ce est une fonction de 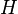$H$ seul, avec 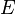$E$ trait?? comme un param??tre. Un rapport de deux fonctions de vraisemblance est appel?? un rapport de vraisemblance, $\ Lambda$ . Par exemple,

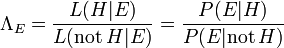$\ Lambda_E = \ frac {L (H | E)} {L (\ mathrm {pas} \, H | E)} = \ frac {P (E | H)} {P (E | \ mathrm {pas} \ , H)}$ ,

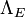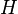o?? la d??pendance de $\ Lambda_E$ sur $H$ est supprim??e pour plus de simplicit?? (comme 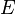$E$ aurait pu ??tre, sauf que nous aurons besoin d'utiliser ce param??tre ci-dessous).

Depuis 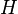$H$ et non- 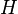$H$ sont mutuellement exclusives et couvrent toutes les possibilit??s, la somme pr??c??demment donn??e pour la probabilit?? marginale r??duit ?? 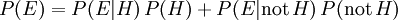$P (E) = P (E | H) \, P (H) + P (E | \ mathrm {pas} \, H) \, P (\ mathrm {pas} \, H)$ . Par cons??quent, nous pouvons r????crire le th??or??me de Bayes que

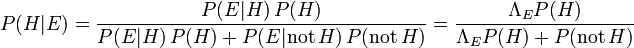$P (H | E) = \ frac {P (E | H) \, P (H)} {P (E | H) \, P (H) + P (E | \ mathrm {pas} \, H) \, P (\ mathrm {pas} \, H)} = \ frac {\ Lambda_E P (H)} {\ Lambda_E P (H) + P (\ mathrm {pas} \, H)}$ .

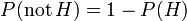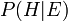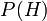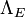Nous pourrions alors exploiter l'identit?? $P (\ mathrm {pas} \, H) = 1 - P (H)$ ?? exposer $P (H | E)$ en fonction de la juste $P (H)$ (Et $\ Lambda_E$ , Qui est calcul?? directement ?? partir de la preuve).

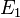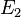Avec deux pi??ces ind??pendantes de preuve $E_1$ et $E_2$ , Inf??rence bay??sienne peut ??tre appliqu??e de mani??re it??rative. Nous pourrions utiliser le premier ??l??ment de preuve pour calculer une probabilit?? post??rieure initiale, puis utiliser cette probabilit?? a posteriori comme une nouvelle probabilit?? a priori pour calculer une seconde probabilit?? a posteriori donn??e le deuxi??me ??l??ment de preuve. Le th??or??me de Bayes donne appliqu?? de mani??re it??rative

$P (H | E_1 \ cap E_2) = \ frac {P (E_2 | H) \; P (E_1 | H) \, P (H)} {P (E_2) \; P (E_1)}$

Utilisation de rapports de vraisemblance, nous constatons que

$P (H | E_1 \ cap E_2) = \ frac {\ Lambda_1 \ Lambda_2 P (H)} {[\ Lambda_1 P (H) + P (\ mathrm {pas} \, H)] \; [\ Lambda_2 P ( H) + P (\ mathrm {pas} \, H)]}$ ,

Cette it??ration de l'inf??rence bay??sienne pourrait ??tre ??tendue avec des morceaux plus ind??pendantes de preuve.

Inf??rence bay??sienne est utilis??e pour calculer les probabilit??s pour la prise de d??cision en situation d'incertitude. En plus des probabilit??s, une fonction de perte doit ??tre ??valu?? pour tenir compte de l'impact relatif des alternatives.

Des exemples simples de l'inf??rence bay??sienne

?? partir de laquelle bol est le cookie?

Pour illustrer, supposons qu'il y ait deux coupes pleines de biscuits. Bowl n ?? 1 a 10 p??pites de chocolat et 30 biscuits secs, tout en bol n ?? 2 a 20 de chaque. Notre ami Fred prend un bol au hasard, puis prend un cookie au hasard. On peut supposer qu'il n'y a pas de raison de croire Fred traite une cuvette diff??remment d'un autre, m??me pour les cookies. Le cookie se av??re ??tre un simple. Comment est-il probable que Fred a pris hors de bol n ?? 1?

Intuitivement, il semble clair que la r??ponse devrait ??tre plus de la moiti??, car il ya des cookies plus simples dans un bol # 1. La r??ponse pr??cise est donn??e par le th??or??me de Bayes. Laisser 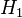$H_1$ correspondre ?? bol n ?? 1, et 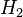$H_2$ bol # 2. Elle est donn??e que les bols sont identiques du point de vue de Fred, ainsi 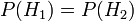$P (H_1) = P (H_2)$ , Et les deux doivent ??tre ??gales ?? 1, de sorte que les deux sont ??gaux ?? 0,5. L'??v??nement 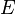$E$ est l'observation d'un cookie plaine. 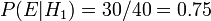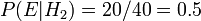A partir des contenus des cuvettes, on sait que $P (E | H_1) = 30/40 = 0,75$ et $P (E | H_2) = 20/40 = 0,5$ . La formule de Bayes donne alors

$\ Begin {matrix} P (H_1 | E) & = & \ frac {P (E | H_1) \, P (H_1)} {P (E | H_1) \, P (H_1) \; + \; P ( E | H_2) \, P (H_2)} \\ \\ \ & = & \ frac {0,75 \ fois 0,5} {\ 0,75 fois 0,5 + 0,5 \ times 0,5} \\ \\ \ & = & 0,6 \ end { matrix}$

Avant nous avons observ?? le cookie, la probabilit?? nous avons attribu?? pour Fred ayant choisi bol n ?? 1 ??tait la probabilit?? a priori, 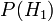$P (H_1)$ , Qui ??tait de 0,5. Apr??s avoir observ?? le cookie, nous devons r??viser la probabilit?? de 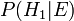$P (H_1 | E)$ , Qui est de 0,6.

Les faux positifs dans un test m??dical

Les faux positifs se produisent lorsque un test faussement ou mal fait ??tat d'un r??sultat positif. Par exemple, un test m??dical pour une maladie peut renvoyer un r??sultat positif indiquant que le patient a une maladie, m??me si le patient n'a pas la maladie. Nous pouvons utiliser le th??or??me de Bayes pour d??terminer la probabilit?? qu'un r??sultat positif est en fait un faux positif. Nous constatons que si une maladie est rare, alors la majorit?? des r??sultats positifs peut ??tre faux positifs, m??me si le test est exacte.

Supposons qu'un test pour une maladie g??n??re les r??sultats suivants:

Si un patient a test?? la maladie, le test renvoie un r??sultat positif 99% du temps, ou avec une probabilit?? de 0,99
Si un patient test?? n'a pas la maladie, le test renvoie un r??sultat positif de 5% du temps, ou avec une probabilit?? de 0,05.

Na??vement, on pourrait penser que seulement 5% des r??sultats positifs sont faux, mais ce est tout ?? fait tort, comme nous le verrons.

Supposons que seulement 0,1% de la population a cette maladie, de sorte que le patient s??lectionn?? au hasard a une probabilit?? a priori d'avoir la maladie 0,001.

Nous pouvons utiliser le th??or??me de Bayes pour calculer la probabilit?? qu'un r??sultat positif est un faux positif.

Soit A repr??sente la condition dans laquelle le patient pr??sente la maladie, et B repr??sentent la d??position d'un r??sultat de test positif. Ensuite, la probabilit?? que le patient a effectivement la maladie ??tant donn?? le r??sultat de test positif est

$\ Begin {matrix} P (A | B) & = & \ frac {P (B | A) P (A)} {P (B | A) P (A) + P (B | \ mathrm {pas} \ , A) P (\ mathrm {pas} \, A)} \\ \\ & = & \ frac {0,99 \ fois 0,001} {\ 0,99 fois 0,001 + 0,05 \ times 0,999} ~ \\ \\ & \ approx & 0 0,019. \ end {matrix}$

et donc la probabilit?? qu'un r??sultat positif est un faux positif est d'environ 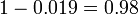$1 ?? 0,019 = 0,98$ , Ou 98%.

Malgr?? la haute pr??cision apparente de l'essai, l'incidence de la maladie est si faible que la grande majorit?? des patients s??ropositifs ne ont pas la maladie. N??anmoins, la fraction des patients s??ropositifs qui ne ont la maladie (0,019) est 19 fois la fraction de personnes qui ne ont pas encore pass?? le test qui ont la maladie (0,001). Ainsi, le test ne est pas inutile, et re-tests peut am??liorer la fiabilit?? du r??sultat.

Afin de r??duire le probl??me des faux positifs, un test doit ??tre tr??s pr??cis dans des rapports de r??sultat n??gatif lorsque le patient n'a pas la maladie. Si le test a rapport?? un r??sultat n??gatif chez les patients sans la maladie avec une probabilit?? de 0,999, alors

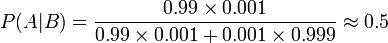$P (A | B) = \ frac {0,99 \ fois 0,001} {\ 0,99 fois 0,001 + 0,001 0,999} \ times \ environ 0,5$ ,

de sorte que 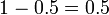$1 ?? 0,5 = 0,5$ Il est maintenant la probabilit?? d'un faux positif.

D'autre part, faux n??gatifs se produisent lorsque un test faussement ou mal fait ??tat d'un r??sultat n??gatif. Par exemple, un test m??dical pour une maladie peut renvoyer un r??sultat n??gatif indiquant que le patient n'a pas une maladie, m??me si le patient a r??ellement la maladie. Nous pouvons ??galement utiliser le th??or??me de Bayes pour calculer la probabilit?? d'un faux n??gatif. Dans le premier exemple ci-dessus,

$\ Begin {matrix} P (A | \ mathrm {pas} \, B) & = & \ frac {P (\ mathrm {pas} \, B | A) P (A)} {P (\ mathrm {} pas \, B | A) P (A) + P (\ mathrm {pas} \, B | \ mathrm {pas} \, A) P (\ mathrm {pas} \, A)} \\ \\ & = & \ frac {0,01 \ fois 0,001} {\ 0,01 fois 0,001 + 0,95 \ times 0,999} \, \\ ~ \\ & \ & environ 0,0000105 \,. \ end {matrix}$

La probabilit?? qu'un r??sultat n??gatif est un faux n??gatif est d'environ 0,00105% ou 0.0000105. Quand une maladie est rare, les faux n??gatifs ne seront pas un probl??me majeur avec le test.

Mais si 60% de la population avait la maladie, alors la probabilit?? d'un faux n??gatif serait plus grande. Avec le test ci-dessus, la probabilit?? d'un faux n??gatif serait

$\ Begin {matrix} P (A | \ mathrm {pas} \, B) & = & \ frac {P (\ mathrm {pas} \, B | A) P (A)} {P (\ mathrm {} pas \, B | A) P (A) + P (\ mathrm {pas} \, B | \ mathrm {pas} \, A) P (\ mathrm {pas} \, A)} \\ \\ & = & \ frac {0,01 \ fois 0,6} {\ 0,01 fois 0,6 + 0,95 \ times 0,4} \, \\ ~ \\ & \ & environ 0,0155 \,. \ end {matrix}$

La probabilit?? qu'un r??sultat n??gatif est un faux n??gatif se ??l??ve ?? 0,0155 ou 1,55%.

Dans la salle d'audience

Inf??rence bay??sienne peut ??tre utilis?? dans un cadre judiciaire par un des jur??s de se accumuler de mani??re coh??rente les preuves pour et contre la culpabilit?? de l'accus??, et de voir si, dans sa totalit??, il satisfait leur seuil personnelle pour ??au-del?? de tout doute raisonnable??.

Laisser 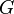$Sol$ d??signer le cas o?? l'accus?? est coupable.

Laisser 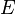$E$ d??signer le cas o?? l'ADN de l'accus?? correspond ?? l'ADN trouv?? sur les lieux du crime.

Laisser 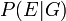$P (E | G)$ d??signer la probabilit?? de l'??v??nement voir 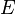$E$ si le d??fendeur est effectivement coupable. (Habituellement, cela serait consid??r?? comme unit??.)

Laisser 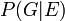$P (G | E)$ d??signer la probabilit?? que l'accus?? est coupable en supposant que le match de l'ADN (??v??nement $E$ ).

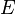Laisser 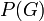$P (G)$ d??signer estimation personnelle du jur?? de la probabilit?? que l'accus?? est coupable, sur la base de la preuve autre que le match d'ADN. Ce pourrait ??tre bas?? sur ses r??ponses au titre du questionnement, ou la preuve pr??sent??e pr??c??demment.

Inf??rence bay??sienne nous dit que si nous pouvons attribuer une probabilit?? p (G) ?? la culpabilit?? de l'accus?? avant de prendre la preuve d'ADN en compte, alors nous pouvons r??viser cette probabilit?? ?? la probabilit?? conditionnelle 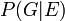$P (G | E)$ Car

$P (G | E) = \ frac {P (G) P (E | G)} {P (E)}$

Supposons, sur la base d'autres ??l??ments de preuve, un jur?? d??cide qu'il ya une chance de 30% que l'accus?? est coupable. Supposons ??galement que le t??moignage judiciaire ??tait que la probabilit?? qu'une personne choisie au hasard aurait ADN qui correspondait ?? celui ?? la sc??ne de crime est de 1 sur un million, ou 10 ^-6.

L'??v??nement E peut se produire de deux fa??ons. Soit l'accus?? est coupable (avec une probabilit?? avant 0,3) et donc son ADN est pr??sent avec une probabilit?? 1, ou qu'il est innocent (avec une probabilit?? de 0,7 avant) et il est assez malchanceux pour ??tre l'un des 1 ?? un million le rapprochement des personnes.

Ainsi le jur?? pourrait r??viser son opinion de mani??re coh??rente afin de tenir compte de la la preuve d'ADN comme suit:

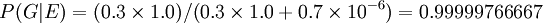$P (G | E) = (0,3 \ 1,0 fois) /(0.3 \ times 1,0 + 0,7 \ times 10 ^ {- 6}) = ,99999766667$ .

L'avantage de l'adoption d'une approche bay??sienne est qu'elle donne le jur?? un m??canisme formel pour combiner la preuve pr??sent??e. L'approche peut ??tre appliqu??e successivement ?? tous les ??l??ments de preuve pr??sent??s au tribunal, avec la partie post??rieure d'une ??tape de devenir l'avant pour la prochaine.

Le jur?? aurait encore d'avoir une estimation pr??alable de la probabilit?? de la culpabilit?? avant le premier ??l??ment de preuve est consid??r??. Il a ??t?? sugg??r?? que cela pourrait ??tre raisonnablement la probabilit?? d'une personne al??atoire tir?? de la population admissible de culpabilit??. Ainsi, pour un crime connu pour avoir ??t?? commis par un adulte de sexe masculin vivant dans une ville contenant 50 000 hommes adultes, la probabilit?? a priori initiale appropri??e pourrait ??tre 1/50000.

Ajout jusqu'?? preuve.

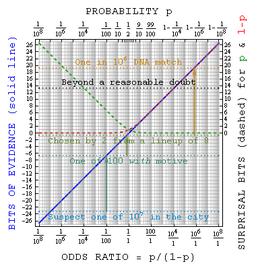
Pour le but d'expliquer le th??or??me de Bayes aux jur??s, il sera g??n??ralement appropri?? de donner dans la forme de Pari plut??t que des probabilit??s, que ceux-ci sont plus largement compris. Dans les Etats th??or??me de Bayes que ce formulaire

cotes post??rieures = ant??rieures cotes x Facteur de Bayes

Dans l'exemple ci-dessus, le jur?? qui a une probabilit?? a priori de 0,3 pour le d??fendeur coupable serait d??sormais exprimer que sous la forme de cote de 3: 7 en faveur de l'accus?? coupable, le facteur de Bayes est d'un million, et la r??sultante cotes post??rieures sont 3 millions ?? 7 ou ?? propos de 429 000 ?? un en faveur de la culpabilit??.

Un approche logarithmique qui remplace multiplication par addition et r??duit la plage des num??ros concern??s pourrait ??tre plus facile pour un jury de g??rer. Cette approche, d??velopp??e par Alan Turing pendant la Seconde Guerre mondiale et plus tard promu par IJ Bien et ET Jaynes entre autres, revient ?? l'utilisation de entropie de l'information.

Au Royaume-Uni, le th??or??me de Bayes a ??t?? expliqu?? au jury sous la forme de cotes par un statisticien t??moin expert dans le cas du viol Regina contre Denis John Adams. Une condamnation a ??t?? fix??e mais le litige en appel, car aucun moyen d'accumulation de preuves avaient ??t?? fournis pour les jur??s qui ne veulent pas utiliser le th??or??me de Bayes. La Cour d'appel a confirm?? la condamnation, mais a ??galement donn?? leur avis que ??Pour introduire le th??or??me de Bayes, ou toute autre m??thode similaire, dans un proc??s criminel plonge le Jury dans les royaumes inappropri??s et inutiles de la th??orie et de la complexit??, les d??viant de leur t??che propre. " Aucune autre appel a ??t?? accueilli et la question de l'??valuation bay??sienne des donn??es d'ADN m??dico-l??gale reste controvers??e.

Gardner-Medwin fait valoir que le crit??re sur lequel devrait se fonder un verdict dans un proc??s criminel ne est pas la probabilit?? de culpabilit??, mais plut??t la probabilit?? de la preuve, ??tant donn?? que le d??fendeur est innocent (semblable ?? un fr??quentiste p-valeur). Il fait valoir que si la probabilit?? post??rieure de culpabilit?? doit ??tre calcul??e par le th??or??me de Bayes, la probabilit?? a priori de culpabilit?? doit ??tre connue. Cela d??pendra de l'incidence de la criminalit??, qui est un ??l??ment de preuve inhabituelle ?? consid??rer dans un proc??s criminel. Consid??rons les trois propositions suivantes:

A: les faits et les t??moignages connus qui auraient pu surgir si l'accus?? est coupable,

B: Les faits et t??moignages connus auraient pu survenir si le d??fendeur est innocent,

C: L'accus?? est coupable.

Gardner-Medwin fait valoir que le jury doit croire ?? la fois A et non-B pour condamner. A et non-B implique la v??rit?? de C, mais l'inverse ne est pas vrai. Il est possible que B et C sont ?? la fois vrai, mais dans ce cas il fait valoir que le jury doit acquitter, m??me se ils savent qu'ils seront laissent certaines personnes coupables en libert??. Voir ??galement Le paradoxe de Lindley.

Autres affaires judiciaires dans lesquelles des arguments probabilistes jou?? un certain r??le ??taient les Howland sera faux proc??s, le Cas Sally Clark, et de la Lucia de Berk cas.

la th??orie de la Recherche

En mai 1968, le sous-marin nucl??aire d'US Scorpion (SSN-589) ne est pas arriv?? comme pr??vu ?? son port d'attache Norfolk, en Virginie. L'US Navy a ??t?? convaincu que le navire avait ??t?? perdu au large de la c??te Est, mais une recherche approfondie ??chou?? ?? d??couvrir l'??pave. Expert en eau profonde de l'US Navy, John Craven USN, a estim?? qu'il ??tait ailleurs et il a organis?? une recherche sud-ouest de la A??ores bas??e sur une triangulation approximative controvers??e par des hydrophones. Il a ??t?? allou?? un seul navire, le Mizar, et il a pris les conseils d'un cabinet de math??maticiens de consultants afin de maximiser ses ressources. Une m??thodologie de recherche bay??sienne a ??t?? adopt??. Commandants de sous-marins exp??riment??s ont ??t?? interrog??s pour construire des hypoth??ses sur ce qui pourrait avoir caus?? la perte du Scorpion.

La zone de la mer a ??t?? divis??e en cases de la grille et une probabilit?? attribu??e ?? chaque carr??, sous chacune des hypoth??ses, de donner un certain nombre de grilles de probabilit??, une pour chaque hypoth??se. Ils ont ensuite ??t?? ajout??s ensemble pour produire une grille globale de probabilit??. La probabilit?? attach?? ?? chaque place ??tait alors la probabilit?? que l'??pave ??tait dans ce carr??. Une seconde grille a ??t?? construit avec des probabilit??s qui repr??sentent la probabilit?? de trouver avec succ??s l'??pave si cette place devait ??tre recherch?? et l'??pave devait ??tre vraiment l??. Ce est une fonction connue de la profondeur de l'eau. Le r??sultat de la combinaison cette grille avec la grille pr??c??dente est une grille qui donne la probabilit?? de trouver l'??pave dans chaque carr?? de la grille de la mer si elle devait ??tre recherch??.

Cette grille de mer ??tait syst??matiquement recherch??e d'une mani??re qui a commenc?? avec les r??gions ??lev??es de probabilit?? premi??re et travaill?? jusque dans les r??gions de faible probabilit?? derniers. Chaque fois qu'un carr?? de la grille a ??t?? fouill?? et trouv?? vide sa probabilit?? a ??t?? r????valu??e en utilisant Le th??or??me de Bayes. Ce ensuite forc?? les probabilit??s de toutes les autres cases de la grille d'??tre r????valu??s (vers le haut), aussi par le th??or??me de Bayes. L'utilisation de cette approche a ??t?? un d??fi majeur pour le calcul du temps, mais il a finalement ??t?? couronn??e de succ??s et le Scorpion a ??t?? retrouv??e ?? environ 740 km sud-ouest de la A??ores en Octobre de cette ann??e. Supposons qu'un carr?? de la grille a une probabilit?? p de contenir l'??pave et que la probabilit?? de d??tecter avec succ??s l'??pave si ce est il ya q. Si la place est fouill?? et aucune ??pave ne est trouv??, alors, par le th??or??me de Bayes, la probabilit?? r??vis??e de l'??pave ??tant sur la place est donn??e par

$p '= \ frac {p (1-q)} {(1-p) + p (1-q)}.$

Plus exemples math??matiques

Classification na??ve bay??sienne

Voir na??ve classificateur de Bayes.

La distribution a posteriori du param??tre binomiale

Dans cet exemple, nous consid??rons le calcul de la distribution a posteriori pour le param??tre binomial. Ce est le m??me probl??me consid??r?? par Bayes dans la proposition 9 de son essai.

On nous donne m observ?? succ??s et ??checs n observ?? dans une exp??rience binomiale. L'exp??rience peut ??tre jeter une pi??ce de monnaie, en tirant une balle dans une urne, ou demander ?? quelqu'un de leur avis, parmi beaucoup d'autres possibilit??s. Ce que nous savons sur le param??tre (appelons-le a) est indiqu?? que la distribution a priori, p (a).

Pour une valeur donn??e de a, la probabilit?? de succ??s en m m + n est essais

$p (m, n | a) = \ begin {} pmatrix n + m \\ m \ end {} pmatrix un ^ m (1-a) ^ n.$

??tant donn?? que m et n sont fixes, et a est inconnu, ce est une fonction de la probabilit?? pour un. De la forme continue de la loi de probabilit?? total, nous avons

$p (a | m, n) = \ frac {p (m, n | a) \, P (A)} {\ ^ int_0 1 p (m, n | a) \, p (a) \, da} = \ frac {\ begin {} pmatrix n + m \\ m \ end {} pmatrix un ^ m (1-a) ^ n \, p (a)} {\ int_0 ^ 1 \ begin {} pmatrix n + m \\ m \ end {} pmatrix un ^ m (1-a) ^ n \, p (a) \, da}.$

Pour certains choix particulier de la distribution a priori p (a), l'int??grale peut ??tre r??solu et la partie arri??re prend une forme commode. En particulier, si p (a) est un la distribution b??ta avec des param??tres m et n _{0 0,} puis la partie post??rieure est ??galement une distribution b??ta avec des param??tres m + ₀ m et n + n _0.

Un Conjugu?? avant est une distribution a priori, tels que la distribution b??ta dans l'exemple ci-dessus, qui a la propri??t?? que la partie post??rieure est le m??me type de distribution.

Ce qui est "bay??sien" ?? propos de la Proposition 9 est que Bayes pr??sent?? comme une probabilit?? pour le param??tre a. Ce est, non seulement une probabilit??s de calcul pour les r??sultats exp??rimentaux, mais aussi pour le param??tre qui les r??git, et m??me l'alg??bre est utilis?? pour faire des inf??rences de type soit possible. Fait int??ressant, Bayes affirme effectivement sa question d'une mani??re qui pourrait faire l'id??e d'attribuer une distribution de probabilit?? ?? un param??tre acceptable pour un fr??quentiste. Il suppose que une boule de billard est jet?? au hasard sur une table de billard, et que les probabilit??s p et q sont les probabilit??s que les boules de billard suivantes tomberont dessus ou en dessous de la premi??re balle. En faisant le param??tre binomial un d??pend d'un ??v??nement al??atoire, il se ??chappe habilement un bourbier philosophique qui ??tait une question qu'il ??tait probablement m??me pas au courant.

Applications informatiques

Inf??rence bay??sienne a des applications dans l'intelligence artificielle et syst??mes experts. Techniques d'inf??rence bay??sienne ont ??t?? un ??l??ment fondamental du informatis??e techniques de reconnaissance des formes depuis la fin des ann??es 1950. Il ya aussi une connexion sans cesse croissant entre les m??thodes bay??sienne et ax??s sur la simulation Monte Carlo techniques puisque les mod??les complexes ne peuvent pas ??tre trait??es sous forme ferm??e par une analyse bay??sienne, tandis que le structure de mod??le graphique inh??rente aux mod??les statistiques, peut permettre algorithmes de simulation efficaces comme le ??chantillonnage de Gibbs et autres R??gimes de l'algorithme de Metropolis-Hastings. R??cemment inf??rence bay??sienne a gagn?? en popularit?? parmi les communaut?? phylog??n??tique pour ces raisons; des applications telles que BEAST, MrBayes et P4 permettre ?? de nombreux param??tres d??mographiques et ??volutifs ?? estimer simultan??ment.

Appliqu?? ?? classification statistique, inf??rence bay??sienne a ??t?? utilis??e ces derni??res ann??es pour d??velopper des algorithmes pour identifier non sollicit?? en vrac e-mail du spam. Les applications qui font usage de l'inf??rence bay??sienne pour le filtrage de spam comprennent DSPAM, Bogofilter, SpamAssassin, InBoxer, et Mozilla. classement de Spam est trait?? plus en d??tail dans l'article sur le na??ve classificateur de Bayes.

Dans certaines applications, la logique floue est une alternative ?? l'inf??rence bay??sienne. La logique floue et l'inf??rence bay??sienne, cependant, sont math??matiquement et s??mantiquement pas compatible: Vous ne pouvez pas, en g??n??ral, comprendre le degr?? de v??rit?? dans la logique floue que la probabilit?? et vice versa.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Bayesian_inference&oldid=202156209 "