M??thode de Monte Carlo

La m??thode de Monte Carlo peut ??tre illustr?? comme un jeu de cuirass??. D'abord, un joueur fait quelques coups al??atoires. Suivant le joueur applique des algorithmes (ie. Un cuirass?? est de quatre points dans le sens vertical ou horizontal). Enfin bas??e sur les r??sultats de l'??chantillonnage al??atoire et l'algorithme le joueur peut d??terminer les emplacements probables des navires de l'autre joueur.

Une m??thode de Monte Carlo est un calcul algorithme qui se appuie sur r??p??t??e ??chantillonnage al??atoire pour calculer ses r??sultats. M??thodes de Monte Carlo sont souvent utilis??s lorsque simulant physiques et math??matiques des syst??mes. En raison de leur d??pendance sur le calcul r??p??t??e et al??atoire ou nombres pseudo-al??atoires, les m??thodes de Monte Carlo sont les plus adapt??s ?? un calcul par ordinateur . M??thodes de Monte Carlo ont tendance ?? ??tre utilis?? lorsqu'il est impossible ou impossible de calculer un r??sultat exact avec un algorithme d??terministe.

Le terme de Monte-Carlo a ??t?? invent?? dans les ann??es 1940 par des physiciens travaillant sur des projets d'armes nucl??aires dans la Los Alamos National Laboratory.

Vue d'ensemble

Il n'y a aucune m??thode de Monte Carlo unique; ?? la place, le terme d??crit une classe importante et largement utilis?? des approches. Cependant, ces approches ont tendance ?? suivre un mod??le particulier:

1. D??finir un domaine d'entr??es possibles.
2. G??n??rer entr??es au hasard dans le domaine, et d'effectuer un calcul d??terministe sur eux.
3. Agr??ger les r??sultats des calculs individuels dans le r??sultat final.

Par exemple, la valeur de π peuvent ??tre estim??s ?? l'aide d'une m??thode Monte Carlo. Dessinez un carr?? sur le sol, puis inscrire un cercle en son sein. Maintenant, saupoudrez quelques petits objets (par exemple, des grains de riz ou de sable) ?? travers la place. Si les objets sont dispers??s uniforme, alors la proportion d'objets dans le cercle doit ??tre d'environ π / 4, qui est le rapport de la superficie du cercle ?? l'aire de la place. Ainsi, si l'on compte le nombre d'objets dans le cercle, multiplier par quatre, et diviser par le nombre d'objets dans la place, nous allons obtenir une approximation de π.

Remarquez comment l'approximation de π suit la tendance g??n??rale des algorithmes de Monte Carlo. Premi??rement, nous d??finissons un domaine d'entr??es: dans ce cas, ce est la place qui entoure notre cercle. Ensuite, nous g??n??rons entr??es au hasard (dispersent grains individuels au sein de la place), puis effectuer un calcul sur chaque entr??e (test si elle tombe dans le cercle). A la fin, nous agr??geons les r??sultats dans notre r??sultat final, le rapprochement des π. Notez ??galement deux autres propri??t??s communes des m??thodes de Monte Carlo: la d??pendance du calcul sur de bons nombres al??atoires, et sa convergence lente ?? une meilleure approximation que plusieurs points de donn??es sont ??chantillonn??es. Si nous suffit de d??poser nos grains dans le centre du cercle, ils pourraient tout simplement se accumulent dans une pile dans le cercle: ils ne seront pas r??partis uniform??ment, et ainsi de notre rapprochement seront loin. Mais se ils sont uniform??ment r??parties, les plus de grains que nous baisser, le plus pr??cis de notre rapprochement des π deviendront.

Histoire

M??thodes de Monte Carlo ont ??t?? initialement pratiqu??es sous des noms plus g??n??riques comme "??chantillonnage statistique". Le nom ??Monte Carlo?? a ??t?? popularis?? par les chercheurs en physique Stanislaw Ulam, Enrico Fermi, John von Neumann , et Nicholas Metropolis, entre autres; le nom est une r??f??rence ?? un c??l??bre casino de Monaco qui l'oncle de Ulam serait emprunter de l'argent pour jouer au. L'utilisation de le hasard et la nature r??p??titive du processus sont analogues aux activit??s men??es dans un casino.

M??thodes al??atoires de calcul et d'exp??rimentation (g??n??ralement consid??r??es comme des formes de simulation stochastique) peut ??tre sans doute remonter aux premiers pionniers de la th??orie des probabilit??s (voir, par exemple, Aiguille de Buffon, et le travail sur de petits ??chantillons par William Gosset), mais sont plus sp??cifiquement remonte ?? l'??re de l'informatique pr??-??lectronique. La diff??rence g??n??rale habituellement d??crit d'une forme de Monte Carlo de la simulation, ce est qu'il "inverse" syst??matiquement le mode typique de simulation, le traitement des probl??mes d??terministes en trouvant d'abord une analogique probabiliste. Les proc??d??s ant??rieurs de simulation et de l'??chantillonnage statistique fait g??n??ralement le contraire: en utilisant la simulation pour tester un probl??me d??terministe pr??c??demment compris. Bien que des exemples d'une approche ??invers???? ne existent historiquement, ils ne ??taient pas consid??r??s comme une m??thode g??n??rale jusqu'?? ce que la popularit?? de la m??thode de Monte Carlo propagation.

Peut-??tre le plus c??l??bre utilisation pr??coce ??tait par Enrico Fermi en 1930, quand il a utilis?? une m??thode al??atoire pour calculer les propri??t??s de la nouvellement d??couvert neutrons . M??thodes de Monte Carlo ont ??t?? au centre de la simulations requises pour la Manhattan Project, mais ont ??t?? s??v??rement limit??e par les outils informatiques ?? l'??poque. Par cons??quent, ce ne est qu'apr??s les ordinateurs ??lectroniques ont d'abord ??t?? construits (?? partir de 1945) que les m??thodes de Monte Carlo ont commenc?? ?? ??tre ??tudi?? en profondeur. Dans les ann??es 1950, ils ont ??t?? utilis??s au Los Alamos pour les premiers travaux portant sur le d??veloppement de la bombe ?? hydrog??ne, et est devenu popularis?? dans les domaines de la physique , chimie physique, et la recherche op??rationnelle . Le Rand Corporation et le US Air Force ??taient deux des principales organisations responsables du financement et de la diffusion d'informations sur les m??thodes de Monte Carlo pendant ce temps, et ils ont commenc?? ?? trouver une large application dans de nombreux domaines diff??rents.

Utilisations des m??thodes de Monte Carlo n??cessitent de grandes quantit??s de nombres al??atoires, et ce ??tait leur utilisation qui a stimul?? le d??veloppement de nombre pseudo-al??atoires g??n??rateurs, qui ??taient beaucoup plus rapide ?? utiliser que les tableaux de nombres al??atoires qui avait ??t?? pr??c??demment utilis??s pour l'??chantillonnage statistique.

Applications

M??thodes de simulation de Monte Carlo sont particuli??rement utiles dans l'??tude des syst??mes avec un grand nombre de degr??s de libert?? coupl??s, tels que les liquides, les mat??riaux d??sordonn??s, solides fortement coupl??s, et les structures cellulaires (voir cellulaire mod??le de Potts). Plus largement, m??thodes de Monte Carlo sont utiles pour la mod??lisation de ph??nom??nes avec significative l'incertitude dans les intrants, tels que le calcul de risques dans les affaires (pour son utilisation dans l'industrie de l'assurance, voir la mod??lisation stochastique). Une utilisation classique est pour l'??valuation des int??grales d??finies , en particulier int??grales multidimensionnelles avec des conditions aux limites complexes.

M??thodes de Monte Carlo en finance sont souvent utilis??s pour calculer la valeur des entreprises, d'??valuer les investissements dans des projets au niveau de l'entreprise ou pour ??valuer des produits financiers d??riv??s. La m??thode de Monte Carlo est destin?? aux analystes financiers qui veulent construire des mod??les stochastiques financiers ou probabilistes par opposition aux mod??les statiques et d??terministes traditionnels.

M??thodes de Monte Carlo sont tr??s importants dans physique computationnelle, chimie physique, et des domaines connexes, appliqu??es et ont diverses applications de compliqu?? chromodynamique quantique calculs ?? la conception boucliers thermiques et formes a??rodynamiques.

M??thodes de Monte Carlo ont ??galement prouv?? son efficacit?? dans la r??solution des ??quations diff??rentielles int??grales coupl??es de champs de rayonnement et transport d'??nergie, et donc ces m??thodes ont ??t?? utilis??es dans calculs de l'illumination globale qui produisent des images photor??alistes de mod??les virtuels en 3D, avec des applications dans les jeux vid??o , l'architecture , conception, g??n??r?? par ordinateur films , effets sp??ciaux du cin??ma, des affaires, de l'??conomie et d'autres domaines.

M??thodes de Monte Carlo sont utiles dans de nombreux domaines des math??matiques de calcul, o?? un choix chanceux peut trouver le bon r??sultat. Un exemple classique est L'algorithme de Rabin pour les tests de primalit??: pour tout n qui ne est pas premier, un x al??atoire a au moins une chance de prouver que n de 75% ne est pas premier. Par cons??quent, si n ne est pas premier, mais x dit qu'il pourrait ??tre, nous avons observ?? au plus un ??v??nement 1-en-4. Si 10 diff??rents x al??atoires disent que ??n est probablement premier" quand il ne est pas, nous avons observ?? un ??v??nement-in-a-million. En g??n??ral, un algorithme de Monte Carlo de ce genre produit une bonne r??ponse avec une garantie n est composite, et x prouve donc, mais une autre sans, mais avec une garantie de ne pas obtenir cette r??ponse quand il a tort trop souvent - dans ce cas au plus 25% du temps. Voir ??galement Algorithme Las Vegas pour un connexe, mais diff??rent, id??e.

Les domaines d'application

Domaines d'application comprennent:

• Graphiques, en particulier pour ray tracing; une version de la Algorithme de Metropolis-Hastings est ??galement utilis?? pour lancer de rayon o?? il est connu sous le nom Transport l??ger Metropolis
• transport l??ger de mod??lisation dans les tissus biologiques
• M??thodes de Monte Carlo en finance
• l'ing??nierie de la fiabilit??
• Dans recuit simul?? pour la pr??diction de la structure des prot??ines
• Dans la recherche de dispositif ?? semiconducteur, pour mod??liser le transport de porteurs de courant
• Sciences de l'environnement, portant sur le comportement des contaminants
• M??thode de Monte Carlo en physique statistique; en particulier, Monte Carlo mod??lisation mol??culaire comme une alternative de calcul pour la dynamique mol??culaire.
• Recherche et sauvetage et lutte contre la pollution. Mod??les utilis??s pour pr??dire la d??rive d'un radeau de sauvetage ou un mouvement d'une nappe d'hydrocarbures en mer.
• En Conception probabiliste pour simuler et de comprendre les effets de la variabilit??
• En Chimie physique, en particulier pour les simulations impliquant des agr??gats atomiques
• En informatique
  • Algorithme Las Vegas
  • LURCH
  • Computer Go
• Mod??lisation du mouvement des atomes d'impuret?? (ou ions) dans les plasmas de tokamaks existants et (par exemple: DIVIMP).
• Dans exp??rimentale en physique des particules , de la conception d??tecteurs, comprendre leur comportement et la comparaison des donn??es exp??rimentales ?? la th??orie
• Codes physique nucl??aire et des particules en utilisant la m??thode de Monte Carlo:
  • GEANT - La simulation du CERN de particules de haute ??nergie interagissent avec un d??tecteur.
  • CompHEP, PYTHIA - g??n??rateurs Monte-Carlo de collisions de particules
  • MCNP (X) - les codes de transport de rayonnement de LANL
  • EGS - Le code de simulation de Stanford pour le transport coupl?? d'??lectrons et de photons
  • L'outil de Monte Carlo de LLNL pour les calculs de dose de radioth??rapie - Peregrine
  • BEAMnrc - Monte Carlo syst??me de code pour la mod??lisation des sources de radioth??rapie ( De LINAC)
  • PENELOPE - Monte Carlo pour le transport coupl?? de photons et d'??lectrons, avec des applications en radioth??rapie
  • MONK - le code de Serco Assurance pour le calcul de k-efficace des syst??mes nucl??aires
  • Mod??lisation de structures en mousse cellulaires et
  • Mod??lisation de tissu morphogen??se

D'autres proc??d??s employant Monte Carlo

• Mod??les al??atoires assorties, par exemple criticit?? auto-organis??e
• Simulation directe Monte Carlo
• Dynamic m??thode de Monte Carlo
• Kinetic Monte Carlo
• Quantum Monte Carlo
• M??thode quasi-Monte Carlo en utilisant s??quences ?? faible divergence et auto ??vitant promenades
• Semiconductor transport de charge, etc.
• Interactions faisceau d'??chantillons microscopie ??lectronique
• Optimisation stochastique
• Mod??le cellulaire Potts
• Cha??ne de Markov Monte Carlo
• Croix-Entropy M??thode
• Economie Appliqu??e de l'information

Utilisez en math??matiques

En g??n??ral, les m??thodes de Monte Carlo sont utilis??s en math??matiques pour r??soudre divers probl??mes en g??n??rant des nombres al??atoires appropri??es et en observant cette fraction des num??ros ob??issant ?? certains biens ou propri??t??s. La m??thode est utile pour obtenir des solutions num??riques ?? des probl??mes qui sont trop compliqu??s pour r??soudre analytiquement. L'application la plus courante de la m??thode de Monte Carlo est l'int??gration de Monte Carlo.

Int??gration

Les m??thodes d??terministes de l'int??gration num??rique fonctionnent en prenant un certain nombre d'??chantillons r??guli??rement espac??s d'une fonction. En g??n??ral, cela fonctionne tr??s bien pour les fonctions d'une variable. Toutefois, pour les fonctions de vecteurs , les m??thodes de quadrature d??terministes peuvent ??tre tr??s inefficaces. Pour int??grer num??riquement en fonction d'un vecteur ?? deux dimensions, la grille ??quidistants points sur une surface ?? deux dimensions sont n??cessaires. Par exemple, une grille de 10x10 n??cessite 100 points. Si le vecteur poss??de 100 dimensions, le m??me espacement sur la grille exigerait 10 ¹⁰⁰ Points beaucoup trop nombreux pour ??tre calcul??e. 100 dimensions ne est nullement d??raisonnable, puisque dans de nombreux probl??mes physiques, une "dimension" est ??quivalente ?? une degr?? de libert??. (Voir Mal??diction de la dimension.)

M??thodes de Monte Carlo fournissent un moyen de sortir de ce temps-augmentation exponentielle. Aussi longtemps que la fonction en question est raisonnablement bien ??lev??, il peut ??tre estim?? par des points de s??lection au hasard dans l'espace 100 dimensions, et de prendre une sorte de moyenne des valeurs de la fonction en ces points. Par le loi des grands nombres, cette m??thode affiche 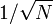convergence-??-dire quadrupler le nombre de points ??chantillonn??s se r??duire de moiti?? l'erreur, quel que soit le nombre de dimensions.

Un raffinement de cette m??thode est de faire en quelque sorte des points al??atoire, mais plus susceptibles de provenir de r??gions de forte contribution ?? l'int??grale que de r??gions de faible contribution. En d'autres termes, les points doivent ??tre tir??es d'une distribution de forme semblable ?? la fonction ?? int??grer. Naturellement, en faisant cela pr??cis??ment est tout aussi difficile que la r??solution de l'int??grale, en premier lieu, mais il existe des m??thodes approximatives disponibles: de la simple constituant une fonction int??grable pens?? pour ??tre similaire, ?? l'une des routines d'adaptation discut??s dans les sujets ??num??r??s ci-dessous.

Une approche similaire consiste ?? utiliser faible ??cart-s??quences ?? la place du m??thode quasi-Monte Carlo. M??thodes quasi-Monte Carlo peuvent souvent ??tre plus efficace ?? l'int??gration num??rique parce que la s??quence "remplit" mieux la r??gion dans un sens et des ??chantillons plus des points les plus importants qui peuvent faire la simulation converge vers la solution souhait??e plus rapidement.

m??thodes d'int??gration

• M??thodes d'??chantillonnage directs
  • ??chantillonnage d'importance
  • L'??chantillonnage stratifi??
  • ??chantillonnage stratifi?? r??cursive
  • Algorithme VEGAS
• Marche al??atoire Monte Carlo y compris Cha??nes de Markov
  • Algorithme de Metropolis-Hastings
• ??chantillonnage de Gibbs

Optimisation

Une autre application puissant et tr??s populaire pour les nombres al??atoires dans la simulation num??rique est en optimisation num??rique. Ces probl??mes utilisent des fonctions de certains vecteur souvent de grandes dimensions qui doivent ??tre r??duits au minimum (ou maximis??). Beaucoup de probl??mes peuvent ??tre formul??es de cette mani??re: par exemple un programme d'??checs de l'ordinateur pourrait ??tre per??u comme essayant de trouver l'ensemble optimal de, disons, 10 se d??place ce qui produit la meilleure fonction d'??valuation ?? la fin. Le probl??me du voyageur de vendeur est un autre probl??me d'optimisation. Il ya aussi des applications ?? la conception d'ing??nierie, tels que optimisation de la conception pluridisciplinaire.

La plupart des m??thodes d'optimisation de Monte Carlo sont bas??es sur marches al??atoires. Essentiellement, le programme se d??placer un marqueur dans l'espace multi-dimensionnel, tendant ?? d??placer dans des directions qui conduisent ?? une fonction inf??rieure, mais se d??pla??ant parfois ?? contre- gradient.

m??thodes d'optimisation

• Strat??gie Evolution
• Les algorithmes g??n??tiques
• Trempe parall??le
• Recuit simul??
• Optimisation stochastique
• Tunneling stochastique

Probl??mes inverses

Formulation probabiliste de probl??mes inverses conduit ?? la d??finition d'une distribution de probabilit?? dans l'espace du mod??le. Cette distribution de probabilit??s moissonneuses-batteuses une information a priori avec de nouvelles informations obtenues en mesurant certains param??tres observables (donn??es). Comme, dans le cas g??n??ral, la th??orie de liaison de donn??es avec les param??tres du mod??le est non lin??aire, la probabilit?? a posteriori dans l'espace de mod??le peut ne pas ??tre facile de d??crire (il peut ??tre multimodal, des moments ne peuvent ??tre d??finis, etc.).

Lorsque l'on analyse un probl??me inverse, l'obtention d'un mod??le de vraisemblance maximale est g??n??ralement pas suffisant, comme on voudra normalement ??galement avoir des informations sur le pouvoir de r??solution des donn??es. Dans le cas g??n??ral, nous pouvons avoir un grand nombre de param??tres du mod??le, et une inspection des densit??s de probabilit?? marginales d'int??r??t peut ??tre difficile, voire inutile. Mais il est possible de produire des pseudo-al??atoire une grande collection de mod??les en fonction de la distribution de probabilit?? post??rieure, et pour analyser et afficher les mod??les de mani??re ?? ce que les informations sur les probabilit??s relatives des propri??t??s mod??le est transport?? vers le spectateur. Ceci peut ??tre accompli au moyen d'une m??thode de Monte Carlo efficace, m??me dans le cas o?? pas de formule explicite pour la distribution a priori ne est disponible.

La m??thode ??chantillonnage d'importance la plus connue, l'algorithme de Metropolis, peut ??tre g??n??ralis??, ce qui donne une m??thode qui permet d'analyser (??ventuellement fortement non lin??aires) probl??mes inverses avec complexe informations a priori et des donn??es avec une distribution de bruit arbitraire. Pour plus de d??tails, voir Mosegaard et Tarantola (1995) Ou Tarantola (2005) .

Monte Carlo et nombres al??atoires

Fait int??ressant, les m??thodes de simulation de Monte Carlo ne n??cessitent g??n??ralement pas vraiment nombres al??atoires soient utiles - pour les autres applications, telles que tests de primalit??, l'impr??visibilit?? est essentiel (voir Davenport (1995)). Beaucoup des techniques les plus utiles utilisent d??terministe, des s??quences pseudo-al??atoires, le rendant facile ?? tester et des simulations de r??installation. La seule qualit?? g??n??ralement n??cessaire de faire bon simulations est pour la s??quence pseudo-al??atoire ?? appara??tre "assez al??atoire" dans un certain sens.

Ce que cela signifie d??pend de l'application, mais g??n??ralement ils doivent passer une s??rie de tests statistiques. Essais que les chiffres sont uniform??ment r??partie ou suivre une autre distribution d??sir??e quand un nombre suffisant d'??l??ments de la s??quence sont consid??r??es est l'un de ceux les plus simples et les plus courants.

Une alternative ?? la m??thode de Monte Carlo de base

??conomie de l'information appliqu??es (AIE) est une m??thode d'analyse de d??cision utilis?? dans les affaires et le gouvernement qui r??pond ?? certaines des lacunes de la m??thode de Monte Carlo - au moins comment il est habituellement utilis?? dans des situations pratiques. Les composants les plus importants AIE ajoute ?? la m??thode de Monte Carlo sont:

1) Comptabilisation de l'exc??s de confiance syst??mique des estimateurs humaines l'??valuation de la probabilit?? ??talonn??e

2) Le calcul de la valeur ??conomique des informations pour guider les mesures empiriques suppl??mentaires

3) En utilisant les r??sultats de Monte Carlos en entr??e ?? l'analyse de portefeuille

Lorsque des simulations de Monte Carlo sont utilis??es dans la plupart des param??tres d'analyse de d??cision, des experts des droits sont utilis??es pour estimer les probabilit??s et les gammes dans le mod??le. Cependant, la recherche de la psychologie d??cision dans le domaine des ??valuations de la probabilit?? calibr??s montre que les humains - en particulier les experts dans divers domaines - ont tendance ?? ??tre trop confiant statistiquement. Ce est, ils ont mis une trop forte probabilit?? qu'un r??sultat pr??vu se produit et ils ont tendance ?? utiliser des plages qui sont trop ??troits pour refl??ter leur incertitude. AIE implique formation estimateurs droits de sorte que les probabilit??s et les plages qu'ils fournissent refl??tent de fa??on r??aliste l'incertitude (ex., Une subjective intervalle de confiance de 90% comme une chance de contenir la valeur r??elle de 90%). Sans cette formation, les mod??les de Monte Carlo seront toujours sous-estimer l'incertitude d'une d??cision et donc le risque.

Un autre inconv??nient est que, dans la pratique, la plupart des utilisateurs de simulations de Monte Carlo reposent enti??rement sur les estimations subjectives initiales et presque jamais suivi avec l'observation empirique. Cela peut ??tre d?? ?? la tr??s grande majorit?? des variables dans de nombreux mod??les et l'incapacit?? des analystes de choisir les variables ??conomiquement justifi??s pour mesurer plus loin. AIE aborde ce en utilisant des m??thodes de la th??orie de la d??cision pour calculer la valeur ??conomique de l'information suppl??mentaire. Ceci ??limine habituellement le besoin de mesurer la plupart des variables et met contraintes pragmatiques sur les m??thodes utilis??es pour mesurer les variables qui ont une valeur de l'information importante.

La derni??re lacune adress??e par l'AIE est que la sortie d'un Monte Carlo - au moins pour l'analyse des d??cisions d'affaires - est tout simplement l'histogramme des rendements r??sultant. N est pr??sent?? crit??res pour d??terminer si une distribution particuli??re des r??sultats est acceptable ou non. Utilisations de l'AIE Th??orie moderne du portefeuille de d??terminer quels investissements sont souhaitables et quelles sont leurs priorit??s relatives devraient ??tre.