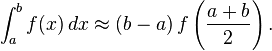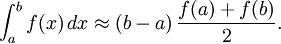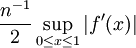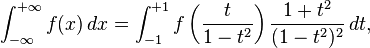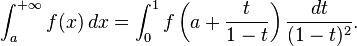L'int??gration num??rique

Renseignements g??n??raux

Cette s??lection Wikipedia est d??connect?? disponibles ?? partir enfants SOS pour la distribution dans le monde en d??veloppement. Visitez le site Web d'enfants SOS au http://www.soschildren.org/

Int??gration num??rique consiste ?? trouver des approximations num??riques pour la valeur $S$

En analyse num??rique, int??gration num??rique constitue une large famille d'algorithmes de calcul de la valeur num??rique d'une certaine int??grante , et par extension, le terme est parfois utilis?? pour d??crire la solution num??rique des ??quations diff??rentielles. Cet article se concentre sur le calcul des int??grales d??finies. La quadrature num??rique terme (souvent abr??g?? en quadrature) est plus ou moins un synonyme pour l'int??gration num??rique, en particulier telle qu'elle est appliqu??e ?? des int??grales unidimensionnelles. L'int??gration num??rique sur plus d'une dimension est parfois d??crit comme cubage, bien que le sens de quadrature est entendu pour l'int??gration de plus grande dimension ainsi.

Le probl??me de base consid??r?? par int??gration num??rique est de calculer une solution approch??e d'une int??grale d??finie:

$\ Int_a ^ b \! f (x) \, dx.$

Si $f (x)$ est une fonction lisse bien comport??s, int??gr?? sur un petit nombre de dimensions et les limites de l'int??gration sont limit??es, il existe de nombreuses m??thodes d'approximation de l'int??grale avec une pr??cision arbitraire.

Raisons de l'int??gration num??rique

Il existe plusieurs raisons pour effectuer une int??gration num??rique. Le f int??grand (x) peut ??tre connu seulement ?? certains points, comme obtenu par ??chantillonnage . Certains syst??mes embarqu??s et d'autres applications informatiques peuvent avoir besoin d'int??gration num??rique pour cette raison.

Une formule pour l'int??grale peut ??tre connu, mais il peut ??tre difficile ou impossible de trouver un primitive qui est une fonction ??l??mentaire. Un exemple d'une telle fonction ?? int??grer est f (x) = exp (- x ^2), dont la primitive (la fonction d'erreur, une fois constants) ne peuvent pas ??tre ??crites dans forme ??l??mentaire.

Il peut ??tre possible de trouver une primitive symboliquement, mais il peut ??tre plus facile ?? calculer une approximation num??rique que de calculer la primitive. Ce est peut-??tre le cas si la primitive est donn??e comme une s??rie infinie ou d'un produit, ou si son ??valuation n??cessite une fonction sp??ciale qui ne est pas disponible.

M??thodes pour int??grales unidimensionnelles

M??thodes d'int??gration num??rique peut g??n??ralement ??tre d??crit comme une combinaison des ??valuations de l'int??grale pour obtenir une approximation de l'int??grale. L'int??grale est ??valu??e ?? un ensemble fini de points appel??s points d'int??gration et une somme pond??r??e de ces valeurs est utilis??e pour calculer l'int??grale. Les points d'int??gration et de poids d??pendent de la m??thode utilis??e et la pr??cision requise de l'approximation.

Une partie importante de l'analyse d'une m??thode d'int??gration num??rique est d'??tudier le comportement de l'erreur d'approximation en fonction du nombre d'??valuations de int??grand. Un proc??d?? qui produit une petite erreur pour un petit nombre d'??valuations est g??n??ralement consid??r?? comme sup??rieur. R??duire le nombre d'??valuations de la fonction ?? int??grer r??duit le nombre d'op??rations arithm??tiques en cause, et donc r??duit le total erreur d'arrondi. En outre, chaque ??valuation prend du temps, et l'int??grale peut ??tre arbitrairement compliqu??e.

Un ??force brute?? type d'int??gration num??rique peut ??tre fait, si l'int??grale est raisonnablement bien comport?? (c.-??- par morceaux continu et de variation born??e), en ??valuant l'int??grant avec de tr??s petits incr??ments.

Quadrature r??gles de base sur les fonctions d'interpolation

Une large classe de r??gles en quadrature peut ??tre d??riv??e par la construction d'interpolation des fonctions qui sont faciles ?? int??grer. G??n??ralement, ces fonctions d'interpolation sont des polyn??mes .

Illustration de la r??gle de rectangle.

La m??thode la plus simple de ce type est de laisser la fonction d'interpolation une fonction constante (un polyn??me de degr?? z??ro) qui passe par le point ((a + b) / 2, f ((a + b) / 2)). Ce est ce qu'on appelle la r??gle milieu ou r??gle rectangle.

$\ Bf int_a ^ (x) \, dx \ environ (ba) \, f \ left (\ frac {a + b} {2} \ right).$

Illustration de la r??gle du trap??ze.

La fonction d'interpolation peut ??tre un fonction affine (un polyn??me de degr?? 1) qui passe par les points (a, f (a)) et (b, f (b)). Ceci est appel?? le r??gle trap??zo??dale.

$\ Bf int_a ^ (x) \, dx \ environ (ba) \, \ frac {f (a) + f (b)} {2}.$

Illustration de la r??gle de Simpson.

Pour l'une de ces r??gles, nous pouvons faire une approximation plus pr??cise en brisant l'intervalle [a, b] en un nombre n de sous-intervalles, le calcul d'un rapprochement pour chaque sous-intervalle, puis en ajoutant jusqu'?? tous les r??sultats. Cela se appelle une r??gle composite, r??gle ??tendue, ou la r??gle it??rative. Par exemple, la r??gle trap??zo??dale composite peut ??tre d??clar?? que

$\ Bf int_a ^ (x) \, dx \ approx \ frac {} {ba n} \ left ({f (a) \ over 2} + \ sum_ {k = 1} ^ {n-1} \ left (f \ left (a + k \ frac {} {ba n} \ right) \ right) {+ f (b) \ over 2} \ right)$

o?? les sous-intervalles sont de la forme [k h, (k + 1) h], avec h = (b - a) / n et k = 0, 1, 2, ..., n-1.

Interpolation avec polyn??mes ??valu??s ?? points ??galement espac??s dans [a, b] donne le Formules de Newton-Cotes, dont la r??gle de rectangle et la r??gle trap??zo??dale sont des exemples. La r??gle de Simpson, qui est bas?? sur un polyn??me d'ordre 2, est ??galement une formule de Newton-Cotes.

r??gles de quadrature avec points ??galement espac??s ont la propri??t?? tr??s pratique de la nidification. La r??gle correspondant ?? chaque intervalle subdivis?? comprend tous les points actuels, de sorte que ces valeurs int??grand peut ??tre r??utilis??.

Si on laisse les intervalles entre les points d'interpolation pour faire varier, nous trouvons un autre groupe de formules de quadrature, tels que la Formules de quadrature de Gauss. Une r??gle de quadrature de Gauss est g??n??ralement plus pr??cise que la r??gle de Newton-Cotes qui exige le m??me nombre d'??valuations de fonctions, si l'int??grale est lisse (ce est ?? dire, si elle est suffisamment diff??rentiables). Autres m??thodes de quadrature avec des intervalles variables comprennent Clenshaw-Curtis quadrature (??galement appel?? quadrature Fej??r) m??thodes, qui font nid.

R??gles de quadrature de Gauss ne nichent pas, mais le connexes Gauss-Kronrod formules de quadrature font.

Algorithmes adaptatifs

Si f (x) n'a pas beaucoup de d??riv??s en tous points, ou si les d??riv??s deviennent grand, alors la quadrature de Gauss est souvent insuffisant. Dans ce cas, un algorithme similaire ?? la suivante sera plus performant:

 def calculate_definite_integral_of_f (f, initial_step_size): '' 'Cet algorithme calcule l'int??grale d??finie d'une fonction 0-1, adaptative, en choisissant petites ??tapes pr??s des points probl??matiques.  '' 'X = 0,0 h = initial_step_size accumulateur = 0,0 tandis x <1.0: si x + h> 1.0: h = 1,0 - x = quad_this_step si error_too_big_in_quadrature_of_over_range (f, [x, x + h]): h = make_h_smaller (h ) else: accumulateur + = quadrature_of_f_over_range (f, [x, x + h]) x + = h si error_too_small_in_quadrature_of_over_range (f, [x, x + h]): h = make_h_larger (h) # ??viter de perdre du temps sur de minuscules ??tapes. retour accumulateur

Certains d??tails de l'algorithme demandent une r??flexion s??rieuse. Pour de nombreux cas, l'estimation de l'erreur de quadrature sur un intervalle d'une fonction f (x) ne est pas ??vidente. Une solution populaire est d'utiliser deux r??gles diff??rentes de quadrature, et d'utiliser leur diff??rence comme une estimation de l'erreur de quadrature. L'autre probl??me est de d??cider ce que ??trop grande?? ou ??tr??s faible?? signifient. Un crit??re local pour "trop grand" est que l'erreur de quadrature ne devrait pas ??tre plus grand que t ?? h o?? t, un nombre r??el, est la tol??rance que nous souhaitons mettre ?? l'erreur globale. Et puis, si h est d??j?? petit, il peut ne pas ??tre int??ressant pour le rendre encore plus petit, m??me si l'erreur de quadrature est apparemment importante. Un crit??re global est que la somme des erreurs sur tous les intervalles doit ??tre inf??rieure ?? t. Ce type d'analyse d'erreur est g??n??ralement appel?? "a posteriori" puisque nous calculons l'erreur apr??s avoir calcul?? le rapprochement.

Heuristiques pour quadrature adaptative sont discut??s par Forsythe et al. (Section 5.4).

m??thodes d'extrapolation

La pr??cision d'une r??gle de quadrature du type Newton-Cotes est g??n??ralement fonction du nombre de points d'??valuation. Le r??sultat est g??n??ralement plus pr??cise que le nombre de points d'??valuation augmente, ou, de mani??re ??quivalente, que la largeur de la taille de pas entre les points diminue. Il est naturel de se demander ce que serait le r??sultat si la taille de l'??tape ont ??t?? autoris??s ?? approcher de z??ro. Cela peut ??tre r??pondu en extrapolant le r??sultat de deux ou plusieurs tailles de pas non nulles, en utilisant m??thodes d'acc??l??ration de s??rie tels que Extrapolation Richardson. La fonction d'extrapolation peut ??tre un polyn??me ou fonction rationnelle. m??thodes d'extrapolation sont d??crites plus en d??tail par Stoer et Bulirsch (section 3.4) et sont mises en ??uvre dans la plupart des routines de la Biblioth??que QUADPACK.

Conservateur (a priori) estimation de l'erreur

Soit f ont une premi??re d??riv??e born??e sur [a, b]. Le valeur moyenne th??or??me pour f, o?? x <b, donne

$(X - a) f '(y_x) = f (x) - f (a) \,$

pour certains y _x dans [a, x] en fonction de x. Si nous int??grons dans x de a ?? b des deux c??t??s et prendre les valeurs absolues, nous obtenons

$\ Left | \ int_a ^ bf (x) \, dx - (b - a) f (a) \ right | = \ left | \ int_a ^ b (x - a) f '(y_x) \, dx \ right |$

Nous pouvons continuer ?? rapprocher l'int??grale sur le c??t?? droit en apportant la valeur absolue en l'int??grant et en rempla??ant le terme dans f 'par une borne sup??rieure:

$\ Left | \ int_a ^ bf (x) \, dx - (b - a) f (a) \ right | \ leq {(b - a) ^ 2 \ over 2} \ sup_ {a \ leq x \ leq b } \ left | f '(x) \ right |$ (**)

(Voir supremum) Par cons??quent, si on approche l'int??grale ∫ _a ^b f (x) d x par la r??gle de quadrature (b -. a) f (a) notre erreur ne est plus grand que le c??t?? droit de (**). On peut convertir en une analyse des erreurs de la somme de Riemann (*), ce qui donne une borne sup??rieure de

${N ^ {- 1} \ over 2} \ sup_ {0 \ leq x \ leq 1} \ left | f '(x) \ right |$

pour le terme d'erreur de ce rapprochement particulier. (Notez que ce est pr??cis??ment l'erreur, nous avons calcul?? pour l'exemple $f (x) = x$ .) Utilisation de plusieurs d??riv??s, et en ajustant la quadrature, nous pouvons faire une analyse d'erreur similaire utilisant une s??rie de Taylor (en utilisant une somme partielle pour une dur??e de reste) pour f. Cette analyse d'erreur donne une stricte limite sup??rieure sur l'erreur, si les d??riv??s de f sont disponibles.

Cette m??thode d'int??gration peut ??tre combin?? avec arithm??tique d'intervalle pour produire des preuves informatiques et calculs v??rifi??s.

Int??grales sur des intervalles infinis

Intervalles infinis

Une fa??on de calculer une int??grale sur l'intervalle infini,

$\ Int _ {- \ infty} ^ {+ \ infty} f (x) \, dx,$

est le transformer en une int??grale sur un intervalle fini par l'un de plusieurs changements possibles de variables, par exemple:

$\ Int _ {- \ infty} ^ {+ \ infty} f (x) \, dx = \ int _ {- 1} ^ {+ 1} f \ left (\ frac {t} {1-t ^ 2} \ right ) \ frac {1 + t ^ 2} {(1-t ^ 2) ^ 2} \, dt,$

L'int??grale sur intervalle fini peut ensuite ??tre ??valu??e par des m??thodes d'int??gration ordinaires.

Intervalles d'une demi-infinis

Une int??grale sur un intervalle de demi-infini peut ??galement ??tre transform?? en une int??grale sur un intervalle fini par l'un de plusieurs changements possibles de variables, par exemple:

$\ Int_a ^ {+ \ infty} f (x) \, dx = \ int_0 ^ 1 f \ left (a + \ frac {t} {1}-t \ right) \ frac {} {dt (1-t) ^ 2}.$

De m??me,

$\ Int _ {- \ infty} ^ af (x) \, dx = \ int_0 ^ 1 f \ left (a - \ frac {1} {t} t \ right) \ frac {} {dt t ^ 2}$

Int??grales multidimensionnelles

Les r??gles en quadrature examin??s jusqu'ici sont tous con??us pour calculer des int??grales unidimensionnelles. Pour calculer des int??grales dans de multiples dimensions, une approche consiste ?? expression multiple entier comme r??p??t??es int??grales unidimensionnelles en faisant appel ?? Th??or??me de Fubini. Cette approche n??cessite des ??valuations de la fonction ?? cro??tre de fa??on exponentielle le nombre de dimensions augmente. Deux proc??d??s sont connus pour r??soudre ce que l'on appelle mal??diction de la dimension.

Monte Carlo

M??thodes de Monte Carlo et m??thodes quasi-Monte Carlo sont faciles ?? appliquer ?? des int??grales multidimensionnelles, et peuvent donner une plus grande pr??cision pour le m??me nombre d'??valuations de la fonction que int??grations r??p??t??es en utilisant des m??thodes unidimensionnelles.

Une grande classe de m??thodes de Monte Carlo utiles sont les soi-disant Cha??nes de Markov algorithmes de Monte Carlo, qui incluent le Algorithme de Metropolis-Hastings et ??chantillonnage de Gibbs.

Grilles Sparse

Sparse grilles ont ??t?? initialement d??velopp??s par Smolyak pour la quadrature des fonctions de haute dimension. La m??thode est toujours bas?? sur un unidimensionnel r??gle de quadrature, mais effectue une combinaison plus sophistiqu??e des r??sultats univari??s.

Connexion avec ??quations diff??rentielles

Le probl??me de l'??valuation de l'int??grale

$\ Int_a ^ b f (x) \, dx$

peut ??tre r??duite ?? un probl??me de valeur initiale pour une ??quation diff??rentielle ordinaire . Si l'int??grale ci-dessus est d??sign?? par I (b), alors la fonction I satisfait

$I '(x) = f (x), \ quad I (a) = 0.$

Les m??thodes d??velopp??es pour les ??quations diff??rentielles ordinaires, tels que M??thodes de Runge-Kutta, peuvent ??tre appliqu??es au probl??me retrait??es et ainsi ??tre utilis??s pour ??valuer l'int??grale. Par exemple, le quatri??me ordre m??thode de Runge-Kutta norme appliqu??e ?? l'??quation diff??rentielle donne la r??gle de Simpson d'en haut.

L'??quation diff??rentielle I '(x) = f (x) a une forme particuli??re: la droite ne contient que la variable d??pendante (ici x) et non la variable ind??pendante (ici I). Cela simplifie la th??orie et les algorithmes consid??rablement. Le probl??me de l'??valuation des int??grales est donc mieux ??tudi?? dans son propre droit.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Numerical_integration&oldid=544151167 "