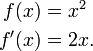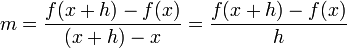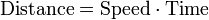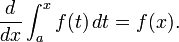Calcul

Calcul ( latine , calcul, une petite pierre utilis?? pour le comptage) est une branche de math??matiques qui comprend l'??tude des limites , d??riv??s , int??grales , et s??rie infinie, et constitue une partie importante de l'enseignement universitaire moderne. Historiquement, il a ??t?? parfois appel?? "le calcul", mais que l'utilisation est rarement vu aujourd'hui. Calcul a des applications r??pandues dans la science et l'ing??nierie et est utilis?? pour r??soudre des probl??mes complexes pour lesquels l'alg??bre seule est insuffisante. Calcul se appuie sur l'alg??bre , la trigonom??trie et g??om??trie analytique et comprend deux branches principales, calcul diff??rentiel et calcul int??gral , qui sont li??s par le th??or??me fondamental du calcul . En math??matiques plus avanc??es, le calcul est g??n??ralement appel?? analyse et est d??finie comme l'??tude des fonctions .

Plus g??n??ralement, le calcul peut se r??f??rer ?? ne importe quelle m??thode ou d'un syst??me de calcul.

Histoire

Aryabhatta avec d'autres math??maticiens indiens au cours des si??cles apport?? une contribution importante au domaine du calcul.

Sir Isaac Newton est un des plus c??l??bres contributeurs au d??veloppement du calcul les, avec, entre autres choses, l'utilisation du calcul dans ses lois du mouvement et de la gravitation.

D??veloppement

L'histoire de calcul tombe en plusieurs p??riodes distinctes, notamment l' ancienne , m??di??vale , et p??riodes modernes. La p??riode antique introduit certaines des id??es du calcul int??gral, mais ne semble pas avoir d??velopp?? ces id??es d'une mani??re rigoureuse et syst??matique. Calcul des volumes et des domaines, la fonction de base du calcul int??gral, on peut faire remonter ?? la ??gyptien Moscou papyrus (c. 1800 BC), dans lequel un Egyptien calcul?? avec succ??s le volume de d'une pyramidale tronc. De l'??cole de Math??matiques grecques, Eudoxe (c. 408-355 BC) a utilis?? le m??thode de l'??puisement, qui pr??figure le concept de la limite, pour calculer les zones et les volumes tout d'Archim??de (c. 287-212 BC) a d??velopp?? cette id??e plus loin, inventer heuristiques qui ressemblent calcul int??gral . Le m??thode de l'??puisement a ??t?? plus tard utilis?? dans Chine par Liu Hui dans le 3??me si??cle apr??s JC afin de trouver l'aire d'un cercle. Il a ??galement ??t?? utilis?? par Zu Chongzhi dans le 5??me si??cle de notre ??re, qui l'a utilis?? pour trouver le volume d'une sph??re .

En l'an 499 l' indienne math??maticien Aryabhata utilis?? la notion de infinit??simaux et ont exprim?? un probl??me astronomique sous la forme d'une base ??quation diff??rentielle . Cette ??quation a finalement conduit Bhāskara II au 12??me si??cle pour d??velopper un d??but d??riv?? repr??sentant changement infinit??simal, et il a d??crit une forme pr??coce de " Th??or??me de Rolle ". Vers l'an 1000, le Math??maticien islamique Ibn al-Haytham (Alhazen) fut le premier ?? tirer la formule pour la somme de la quatri??me pouvoir , et l'aide induction math??matique, il a d??velopp?? une m??thode qui est facilement g??n??ralisable ?? trouver la formule pour la somme de toutes les int??grales des pouvoirs, ce qui ??tait fondamental pour le d??veloppement du calcul int??gral. Au 12??me si??cle, le Persan math??maticien Sharaf al-Din al-Tusi a d??couvert le d??riv?? de polyn??mes cubiques, un r??sultat important dans le calcul diff??rentiel. Au 14??me si??cle, Madhava de Sangamagrama, avec d'autres math??maticiens-astronomes de la ??cole du Kerala, a d??crit des cas particuliers de s??rie de Taylor , qui sont trait??s dans le texte Yuktibhasa.

A l'??poque moderne, les d??couvertes ind??pendants en calcul ont ??t?? faites au d??but de 17??me si??cle Japon, par des math??maticiens tels que Seki Kowa, qui est compl??t??e par la m??thode de l'??puisement. En Europe, la seconde moiti?? du 17??me si??cle ??tait une p??riode de grande innovation. Calcul fourni une nouvelle occasion en physique math??matique pour r??soudre des probl??mes de longue date. Plusieurs math??maticiens ont contribu?? ?? ces avanc??es, notamment John Wallis et Isaac Barrow. James Gregory se est av??r?? un cas particulier de la seconde th??or??me fondamental du calcul dans AD 1668.

Gottfried Wilhelm Leibniz a ??t?? accus?? de le plagiat d'??uvres in??dites de Sir Isaac Newton, mais est maintenant consid??r?? comme un inventeur ind??pendant et collaborateur vers calcul.

Leibniz et Newton tir?? ces id??es dans un ensemble coh??rent et ils sont g??n??ralement cr??dit?? de l'invention ind??pendante et presque simultan??e de calcul. Newton a ??t?? le premier ?? appliquer le calcul au g??n??ral physique et Leibniz a d??velopp?? une grande partie de la notation utilis??e dans le calcul d'aujourd'hui; il a souvent pass?? des jours d??termination symboles appropri??s pour les concepts. L'id??e de base que les deux Newton et Leibniz avaient ??t?? le th??or??me fondamental du calcul .

Lorsque Newton et Leibniz publi??es pour la premi??re de leurs r??sultats, il y avait grande controverse sur laquelle math??maticien (et donc quel pays) m??rit?? cr??dit. Newton tirait ses r??sultats du premier, mais Leibniz publi?? pour la premi??re. Newton selon Leibniz a vol?? les id??es de ses notes in??dites, que Newton avait partag?? avec quelques membres de la Royal Society. Cette controverse divis?? math??maticiens de math??maticiens continentaux anglophone depuis de nombreuses ann??es, au d??triment des math??matiques en anglais. Un examen attentif des documents de Leibniz et Newton montre qu'ils sont arriv??s ?? leurs r??sultats de fa??on ind??pendante, avec Leibniz commen??ant d'abord avec l'int??gration et Newton ?? la diff??renciation. Aujourd'hui, ?? la fois Newton et Leibniz sont donn?? le cr??dit pour le d??veloppement de calcul ind??pendamment. Il est Leibniz, cependant, qui a donn?? la nouvelle discipline son nom. Newton a appel?? son calcul " la science de fluxions ".

Depuis l'??poque de Leibniz et Newton, de nombreux math??maticiens ont contribu?? ?? la poursuite du d??veloppement du calcul. Au 19??me si??cle, le calcul a ??t?? mis sur un pied beaucoup plus rigoureuse par les math??maticiens tels que Cauchy, Riemann , et Weierstrass. Ce est ??galement durant cette p??riode que les id??es du calcul ont ??t?? g??n??ralis??s ?? l'espace euclidien et plan complexe . Lebesgue encore g??n??ralis?? la notion de l'int??grale.

Calcul est un sujet omnipr??sent dans la plupart des ??coles et des universit??s modernes, et les math??maticiens du monde entier continuent ?? contribuer ?? son d??veloppement.

Importance

Bien que certaines des id??es du calcul ont ??t?? d??velopp??s plus t??t, en Gr??ce, La Chine, l'Inde , L'Irak, la Perse et Le Japon, l'utilisation moderne de calcul a commenc?? en l'Europe , au cours du 17??me si??cle, lorsque Isaac Newton et Gottfried Wilhelm Leibniz construits sur les travaux de math??maticiens ant??rieures ?? introduire les principes de base du calcul. Ce travail a eu un impact fort sur le d??veloppement de la physique .

Applications du calcul diff??rentiel incluent les calculs impliquant la vitesse et l'acc??l??ration , les la pente d'une courbe, et optimisation. Applications du calcul int??gral comprennent les calculs impliquant la zone , le volume , longueur de l'arc, centre de masse , le travail , et pression. Des applications plus avanc??es comprennent s??rie de puissance et s??rie de Fourier. Calcul peut ??tre utilis?? pour calculer la trajectoire d'un amarrage de la navette ?? une station spatiale ou la quantit?? de neige dans une all??e.

Calcul est ??galement utilis?? pour acqu??rir une compr??hension plus pr??cise de la nature de l'espace, le temps et le mouvement. Pendant des si??cles, les math??maticiens et les philosophes ont lutt?? avec les paradoxes impliquant division par z??ro ou sommes d'une infinit?? de nombres. Ces questions se posent dans l'??tude du mouvement et de la zone . Le grec ancien philosophe Zeno a donn?? plusieurs exemples c??l??bres de cette paradoxes. Calcul fournit des outils, en particulier la limite et de la s??rie infinie, qui r??sout les paradoxes.

Fondations

En math??matiques, les fondations se r??f??re ?? la d??veloppement rigoureux d'un sujet ?? partir d'axiomes et de d??finitions pr??cises. Travailler sur une base rigoureuse pour le calcul math??maticiens occup?? pendant la majeure partie du si??cle suivant Newton et Leibniz et est encore dans une certaine mesure un domaine de recherche actif aujourd'hui.

Il ya plus d'une approche rigoureuse ?? la fondation de calcul. L'une est d'habitude via le concept de limites d??finies sur la continuum de nombres r??els . Une autre solution consiste analyse non standard, dans lequel le syst??me de nombre r??el est augment??e avec infinit??simale et nombres infinis. Les bases de calcul sont inclus dans le domaine de la analyse r??elle, qui contient les d??finitions compl??tes et des preuves des th??or??mes du calcul ainsi que des g??n??ralisations telles que th??orie de la mesure et th??orie de la distribution.

Principes

Limites et Infinitesimals

Calcul est g??n??ralement d??velopp?? par la manipulation de tr??s petites quantit??s. Historiquement, la premi??re m??thode de le faire ??tait de infinit??simaux. Ce sont des objets qui peuvent ??tre trait??s comme des num??ros, mais qui sont, en quelque sorte, "infiniment petit". Sur une ligne de nombre, ceux-ci seraient des endroits qui ne sont pas ?? z??ro, mais qui ont une distance nulle de z??ro. Aucune nombre non-nul est un infinit??simal, parce que sa distance de z??ro est positif. Tout multiple d'un infinit??simal est toujours infiniment petit, en d'autres termes, infinit??simaux ne r??pondent pas ?? la Archim??dien. De ce point de vue, le calcul est un ensemble de techniques permettant de manipuler infinit??simaux. Ce point de vue est tomb?? en disgr??ce au 19??me si??cle, car il est difficile de faire la notion de pr??cision infinit??simale. Cependant, le concept a ??t?? relanc?? dans le 20??me si??cle avec l'introduction de analyse non-standard, qui a fourni des bases solides pour la manipulation des infinit??simaux.

Au 19??me si??cle, infiniment ont ??t?? remplac??s par des limites . Limites d??crivent la valeur d'une fonction ?? une certaine entr??e en fonction de ses valeurs de l'entr??e ?? proximit??. Ils capturent le comportement ?? petite ??chelle, comme infinit??simales, mais en utilisant des nombres ordinaires. De ce point de vue, le calcul est un ensemble de techniques de manipulation de certaines limites. Infinitesimals se remplac??s par de tr??s petits nombres, et l'infiniment petit comportement de la fonction est trouv?? en prenant le comportement limite pour les num??ros plus en plus petits. Limites sont faciles ?? mettre sur des bases rigoureuses, et pour cette raison ils sont l'approche standard pour le calcul.

D??riv??s

Tangente au (x, f (x)). Le d??riv?? f '(x) d'une courbe en un point est la pente (mont??e sur la distance) de la ligne tangente ?? cette courbe ?? ce point.

Le calcul diff??rentiel est l'??tude de la d??finition, propri??t??s et applications de la d??riv??e ou pente d'un graphique. Le processus de trouver le d??riv?? est appel?? diff??renciation. En langage technique, le d??riv?? est un op??rateur lin??aire, qui entre en fonction et ??met une deuxi??me fonction, de sorte qu'en chaque point la valeur de la sortie est la pente de l'entr??e.

Le concept du d??riv?? est fondamentalement plus avanc?? que les concepts rencontr??s dans l'alg??bre. En alg??bre, les ??l??ves apprennent sur les fonctions qui entrer un num??ro et la sortie un autre num??ro. Par exemple, si les entr??es de la fonction de doublement 3, puis il d??livre en sortie 6, tandis que si les entr??es de la fonction d'??l??vation au carr?? 3, il d??livre 9. Mais les d??riv??s entr??es et sorties d'une fonction une autre fonction. Par exemple, si les entr??es d??riv??s de fonction d'??l??vation au carr??, alors il envoie la fonction de doublement, parce que la fonction de doublement donne la pente de la fonction quadrature ?? un moment donn??.

Pour comprendre le d??riv??, les ??l??ves doivent apprendre la notation math??matique. Dans la notation math??matique, un symbole commun pour la d??riv??e d'une fonction est une marque apostrophe comme appel?? Premier. Ainsi la d??riv??e de f est f '(parl?? "f prime"). La derni??re phrase de l'alin??a pr??c??dent, dans la notation math??matique, serait ??crit

Si l'entr??e est une fonction de temps, alors la d??riv??e de cette fonction est la vitesse ?? laquelle la fonction change.

Si une fonction est lin??aire (qui est, si le graphe de la fonction est une ligne droite), la fonction peut ??tre ??crit y = mx + b, o??:

.

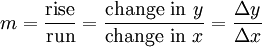Cela donne une valeur exacte pour la pente d'une ligne droite. Si la fonction ne est pas une ligne droite, cependant, alors le changement y divis?? par le changement de x varie, et nous pouvons utiliser le calcul pour trouver une valeur exacte ?? un moment donn??. (Notez que y et f (x) repr??sentent la m??me chose:. La sortie de la fonction) La droite passant par deux points d'une courbe est appel??e une ligne s??cante. La pente, ou mont??e sur la distance, d'une s??cante peuvent ??tre exprim??s en

o?? le Les coordonn??es du premier point sont (x, f (x)) et h est la distance horizontale entre les deux points.

Pour d??terminer la pente de la courbe, nous utilisons la limite:

.

Travailler sur un cas particulier, nous trouvons la pente de la fonction de mise au carr?? ?? l'endroit o?? l'entr??e est de 3 et la sortie est neuf (ce est ?? dire, f (x) = x ^2, alors f (3) = 9).

La pente de la fonction de mise au carr?? au point (3, 9) est de 6, ce est-??-dire, il va jusqu'?? six fois plus vite que ??a va vers la droite.

Le processus de limite vient d'??tre d??crit peut ??tre g??n??ralis?? ?? tout point sur le graphique d'une fonction. La proc??dure peut ??tre visualis?? comme dans la figure suivante.

Tangente comme une limite de droites s??cantes. La d??riv??e f '(x) d'une courbe en un point est la pente de la droite tangente ?? la courbe en ce point. Cette pente est d??termin??e en consid??rant la valeur limite des pentes des droites s??cantes.

Ici, la fonction concern??e (dessin??e en rouge) est f (x) = x ³ - x. La ligne de tangente (en vert) qui passe par le point (-3/2, -15 / 8) a une pente de 23/4. A noter que les ??chelles verticale et horizontale de l'image sont diff??rentes.

Int??grales

Calcul int??gral est l'??tude des d??finitions, propri??t??s et applications de deux concepts li??s, l'int??grale ind??finie et l'int??grale d??finie. Le processus de recherche de la valeur d'une int??grale est appel?? int??gration. En langage technique, ??tudie calcul int??gral deux connexes op??rateurs lin??aires.

L'int??grale ind??finie est la primitive, l'op??ration inverse de la d??riv??e. F est une int??grale ind??finie de f lorsque f est un d??riv?? de F. (Cette utilisation de lettres majuscules et minuscules pour une fonction et son int??grale ind??finie est commun dans le calcul.)

Les entr??es d'une int??grale d??finie de fonction et d??livre un nombre, ce qui donne la zone situ??e entre la courbe de l'entr??e et l' axe des x . La d??finition technique de l'int??grale d??finie est la limite d'une somme des aires des rectangles, appel??e Somme de Riemann.

Un exemple est motivant les distances parcourues dans un temps donn??.

Si la vitesse est constante, que la multiplication est n??cessaire, mais si les changements de vitesse, alors nous avons besoin d'une m??thode plus puissante de trouver la distance. Un tel proc??d?? consiste ?? approximer la distance parcourue par le temps jusqu'?? la rupture en plusieurs courts intervalles de temps, puis en multipliant le temps ??coul?? dans chaque intervalle de l'une des vitesses dans cet intervalle, et en prenant ensuite la somme (a Riemann somme) de la distance approximative parcourue dans chaque intervalle. L'id??e de base est que si peu de temps se est ??coul??, la vitesse restera plus ou moins la m??me. Cependant, une somme de Riemann ne donne qu'une approximation de la distance parcourue. Nous devons prendre la limite de toutes ces sommes de Riemann pour trouver la distance exacte parcourue.

L'int??gration peut ??tre consid??r??e comme la mesure de l'aire sous une courbe, d??finie par f (x), entre deux points (ici A et B).

Si f (x) dans le diagramme de gauche repr??sente la vitesse car il varie au fil du temps, la distance parcourue entre les temps repr??sent??s par A et B est la zone de la r??gion ombr??e s.

Pour approximer cette zone, une m??thode intuitive consisterait ?? diviser la distance entre a et b en un nombre de segments ??gaux, la longueur de chaque segment repr??sent?? par le symbole Ax. Pour chaque petit segment, nous pouvons choisir une valeur de la fonction f (x). Appelez cette valeur h. Puis l'aire du rectangle avec une base Ax et la hauteur h donne la distance (temps Ax multipli?? par la vitesse h) se sont rendus dans ce segment. Associ??e ?? chaque segment est la valeur moyenne de la fonction au-dessus, f (x) = h. La somme de tous ces rectangles donne une approximation de la zone situ??e entre l'axe et la courbe, qui est une approximation de la distance totale parcourue. Une petite valeur pour Ax donnera plus de rectangles et dans la plupart des cas une meilleure approximation, mais pour une r??ponse exacte nous avons besoin de prendre une limite Ax se rapproche de z??ro.

Le symbole de l'int??gration est , Un S allong?? (qui signifie ??somme??). L'int??grale d??finie se ??crit:

et est en lecture "l'int??grale de a ?? b de f -OF- x par rapport ?? x."

L'int??grale ind??finie, ou primitive, est ??crit:

.

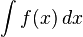Fonctions diff??rant par seulement une constante ont la m??me d??riv??, et donc la primitive d'une fonction donn??e est en fait une famille de fonctions qui ne diff??rent que par une constante. ??tant donn?? que la d??riv??e de la fonction y = x ?? + C, o?? C est une constante quelconque, est y '= x 2, la primitive de celle-ci est donn??e par:

.

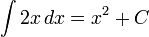Une constante ind??termin??e comme C dans la primitive est connu comme un constante d'int??gration.

Th??or??me fondamental

Le th??or??me fondamental du calcul indique que la diff??renciation et l'int??gration sont des op??rations inverses. Plus pr??cis??ment, elle concerne les valeurs de primitives ?? int??grales d??finies. Car il est g??n??ralement plus facile ?? calculer une primitive que d'appliquer la d??finition d'une int??grale d??finie, le th??or??me fondamental du calcul fournit un moyen pratique de calculer des int??grales d??finies. Il peut ??galement ??tre interpr??t?? comme un expos?? pr??cis du fait que la diff??renciation est l'inverse de l'int??gration.

Le th??or??me fondamental du calcul d??clare: Si une fonction f est continue sur l'intervalle [a, b] et si F est une fonction dont la d??riv??e est f sur l'intervalle (a, b), puis

En outre, pour tout x dans l'intervalle (a, b),

Cette r??alisation, faite ?? la fois par Newton et Leibniz , qui a bas?? leurs r??sultats sur le travail plus t??t par Isaac Barrow, ??tait la cl?? de la prolif??ration massive des r??sultats analytiques apr??s leur travail est devenu connu. Le th??or??me fondamental fournit une m??thode alg??brique de calcul nombreuses int??grales-sans effectuer limites d??finies par les processus pour trouver des formules primitives. Ce est ??galement une solution d'un prototype ??quation diff??rentielle . ??quations diff??rentielles concernent une fonction inconnue ?? ses d??riv??s, et sont omnipr??sents dans les sciences.

Applications

Le de la spirale logarithmique Nautilus shell est une image classique utilis?? pour d??crire la croissance et les changements li??s au calcul

Calcul est utilis?? dans toutes les branches des sciences physiques , en sciences informatiques , les statistiques , l'ing??nierie , l'??conomie , des affaires , la m??decine et dans d'autres domaines o?? un probl??me peut ??tre math??matiquement le mod??le et une solution optimale est souhait??e.

Physique fait usage particulier du calcul; tous les concepts de la m??canique classique sont li??s par calcul. La masse d'un objet de connue densit?? , le moment d'inertie des objets, ainsi que l'??nergie totale d'un objet dans un champ conservateur peut ??tre trouv??e par l'utilisation de calcul. Dans les sous-domaines de l'??lectricit?? et le magn??tisme calcul peut ??tre utilis??e pour trouver le total flux de champs ??lectromagn??tiques. Un exemple plus historique de l'utilisation du calcul en physique est la deuxi??me loi de Newton sur le mouvement , il utilise express??ment le terme ??taux de variation??, qui se r??f??re ?? la d??riv??e: Le taux de changement de la dynamique d'un corps est ??gale ?? la force agissant r??sultante sur le corps et est dans le m??me sens. M??me l'expression commune de la deuxi??me loi de Newton Force = Masse ?? Acc??l??ration implique le calcul diff??rentiel, car l'acc??l??ration peut ??tre exprim??e comme la d??riv??e de la vitesse. La th??orie de Maxwell de l'??lectromagn??tisme et d'Einstein de la th??orie de la relativit?? g??n??rale sont ??galement exprim??s dans la langue du calcul diff??rentiel.

Calcul peut ??tre utilis?? conjointement avec d'autres disciplines math??matiques. Par exemple, il peut ??tre utilis?? avec l'alg??bre lin??aire pour trouver le ??meilleur ajustement?? approximation lin??aire pour un ensemble de points dans un domaine.

Dans le domaine de la m??decine, le calcul peut ??tre utilis??e pour trouver l'angle de branchement optimal d'un vaisseau sanguin de mani??re ?? maximiser les flux.

En g??om??trie analytique , l'??tude des graphiques de fonctions, le calcul est utilis??e pour trouver des points hauts et les points bas (de maximums et minimums), la pente, concavit?? et les points d'inflexion.

En ??conomie, le calcul permet la d??termination du b??n??fice maximal en fournissant un moyen de calculer facilement la fois le co??t marginal et revenu marginal.

Calcul peut ??tre utilis?? pour trouver des solutions aux ??quations approximatives, des m??thodes telles que la m??thode de Newton , Point it??ration fixe, et approximation lin??aire. Par exemple, les engins spatiaux utiliser une variante de la M??thode d'Euler rapprochant cours courbes dans les environnements de gravit?? z??ro.