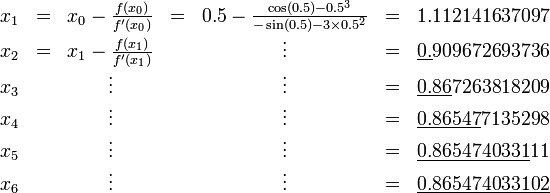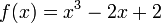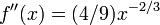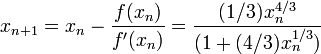La m??thode de Newton

?? propos de ce ??coles s??lection Wikipedia

Les articles de cette s??lection ??coles ont ??t?? organis??s par sujet du programme d'??tudes gr??ce aux b??n??voles d'enfants SOS. SOS Children travaille dans 45 pays africains; pouvez-vous aider un enfant en Afrique ?

En analyse num??rique, la m??thode de Newton (??galement connu sous le nom de Newton Raphson ou la m??thode de Newton-Fourier) est peut-??tre la meilleure m??thode connue pour trouver de meilleures approximations successivement aux z??ros (ou racines) d'un r??el -??valu??es fonction . La m??thode de Newton peut souvent convergent remarquablement rapidement, surtout si l'it??ration commence la racine "assez pr??s" souhait??e. Juste comment proche "suffisamment proche" doit ??tre et ?? quelle vitesse "remarquablement vite" peut ??tre d??pend du probl??me, comme on le verra en d??tail ci-dessous. Malheureusement, loin de la racine souhait??e, la m??thode de Newton peut facilement conduire ?? un utilisateur non averti ??garer et ??garer avec peu d'avertissement. Ainsi, de bonnes impl??mentations du proc??d?? int??grer dans une routine qui d??tecte ??galement les surmonte et peut-??tre des ??checs de convergence possibles.

La m??thode de Newton peut ??galement ??tre utilis?? pour trouver un minimum ou maximum d'une telle fonction, en trouvant un z??ro dans la d??riv??e premi??re de la fonction, voir La m??thode de Newton comme un algorithme d'optimisation.

L'algorithme est le premier dans la classe de Les m??thodes de chef de famille, r??ussi par M??thode de Halley.

Description de la m??thode

L'id??e de la m??thode est la suivante: on part d'une estimation initiale qui est assez proche de la vraie racine, alors la fonction est approch??e par sa tangente (qui peut ??tre calcul?? en utilisant les outils de calcul ), et on calcule x ordonn??e ?? l'origine de cette tangente (qui est fait facilement avec l'alg??bre ??l??mentaire). Ce x ordonn??e ?? l'origine sera typiquement une meilleure approximation de la racine de la fonction que l'estimation initiale, et la m??thode peut ??tre r??it??r??.

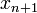Une illustration d'une it??ration de la m??thode de Newton (la fonction f est repr??sent??e en bleu et la ligne tangente est en rouge). Nous voyons que $x_ {n + 1}$ est une meilleure approximation que 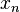$x_n$ pour la racine $x$ de la fonction $fa$ .

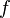Supposons f: [a, b] → R est un diff??rentiable fonction d??finie sur la intervalle [a, b] avec les valeurs dans le nombres r??els R. La formule pour faire converger sur la racine peut ??tre facilement d??duite. Supposons que nous ayons un peu de courant rapprochement x _n. Ensuite, nous pouvons d??duire la formule pour une meilleure approximation, x _{n + 1} en se r??f??rant au sch??ma sur la droite. Nous savons de la d??finition du d??riv?? ?? un moment donn?? que ce est la pente d'une tangente ?? ce point.

C'est

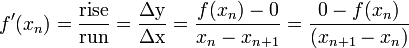$f '(x_ {n}) = \ frac {\ mathrm {lieu}} {\ mathrm {terme}} = \ frac {\ mathrm {\ Delta y}} {\ mathrm {\ Delta x}} = \ frac { f (x_ {n}) - 0} {x_ {n} - x_ {n + 1}} = \ frac {0 - f (x_ {n})} {(x_ {n + 1} - x_ {n} )} \, \!$ .

Ici, f 'repr??sente la d??riv??e de la fonction f. Puis par l'alg??bre simple nous pouvons tirer

$x_ {n + 1} = x_n - \ frac {f (xn)} {f '(xn)} \, \!$ .

Nous commen??ons le processus off avec une valeur initiale arbitraire x _0. (Le plus proche du z??ro, mieux ce est. Mais, en l'absence de toute intuition sur l'endroit o?? pourrait se trouver le z??ro, une ??estimation et v??rifier?? m??thode pourrait r??duire les possibilit??s ?? un assez petit intervalle faisant appel ?? la th??or??me de la valeur interm??diaire.) La m??thode sera g??n??ralement converger, ?? condition que cette supposition initiale est suffisamment proche du z??ro inconnue, et que $f '(x 0) \ neq 0$ . En outre, pour un z??ro de une multiplicit??, la convergence est au moins quadratique (voir vitesse de convergence) dans un voisinage du z??ro, ce qui signifie intuitivement que le nombre de chiffres corrects au moins approximativement double de chaque ??tape. Plus de d??tails peuvent ??tre trouv??s dans la section de l'analyse ci-dessous.

Exemple

Consid??rons le probl??me de trouver le nombre positif x cos (x) = x ^3. On peut reformuler que de trouver le z??ro de f (x) = cos (x) - x ^3. Nous avons f '(x) = sin (x) - 3 x ^2. Depuis cos (x) ≤ 1 pour tout x et x ^3> 1 pour x> 1, nous savons que notre z??ro se situe entre 0 et 1. Nous essayons une valeur de d??part de x ₀ = 0,5.

$\ Begin {matrix} x_1 & = & x_0 - \ frac {f (x 0) {} f '(x 0)} = & & 0,5 - \ frac {\ cos (0,5) - 0,5 ^ 3} {- \ sin (0,5 ) - 3 \ times 0,5 ^ 2} & = & 1,112141637097 \\ x_2 & = & x_1 - \ frac {f (x 1)} {f '(x 1)} & & \ & vdots = & \ underline {} 0. 909672693736 \\ x_3 & & \ & vdots & \ & vdots = & \ underline {0,86} 7263818209 \\ x_4 & & \ & vdots & \ & vdots = & \ underline {} 0,86547 7135298 \\ x_5 & & \ & vdots & \ vdots & = & \ underline {} 0,8654740331 11 \\ & x_6 & \ & vdots & \ & vdots = & \ underline {,865474033102} \ end {matrix}$

Les chiffres corrects sont soulign??s dans l'exemple ci-dessus. En particulier, x ₆ est correcte au nombre de d??cimales donn??. Nous voyons que le nombre de chiffres corrects apr??s la virgule augmente de 2 (pour x ₃₎ ?? 5 et 10, illustrant la convergence quadratique.

Histoire

La m??thode de Newton a ??t?? d??crit par Isaac Newton ?? De analysi par aequationes numero terminorum infinitas (??crit en 1669, publi?? en 1711 par William Jones) et ?? De METODIS fluxionum et serierum infinitarum (??crit en 1671, traduit et publi?? en Fluxion en 1736 par John Colson). Cependant, sa description diff??re sensiblement de la description donn??e ci-dessus moderne: Newton se applique seulement ?? la m??thode des polyn??mes. Il ne calcule pas les approximations successives 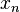$x_n$ , Mais calcule une suite de polyn??mes et seulement ?? la fin, il arrive ?? une approximation de la racine x. Enfin, Newton consid??re la m??thode purement alg??brique et ne remarque pas la connexion avec le calcul. Isaac Newton probablement d??riv?? sa m??thode ?? partir d'une m??thode similaire mais moins pr??cise par Fran??ois Vi??te. L'essence de la m??thode de Vi??te peut ??tre trouv?? dans le travail de la Persique math??maticien Sharaf al-Din al-Tusi (Ypma 1995). Un cas particulier de la m??thode de Newton pour calculer des racines carr??es a ??t?? connu beaucoup plus t??t et est souvent appel?? le M??thode babylonienne.

La m??thode de Newton a ??t?? publi?? la premi??re fois en 1685 dans le Trait?? de l'alg??bre ?? la fois historique et pratique par John Wallis. En 1690, Joseph Raphson publi?? une description simplifi??e Universalis Analyse de aequationum. Raphson nouveau consid??r?? la m??thode de Newton purement comme une m??thode alg??brique et limite son utilisation aux polyn??mes, mais il d??crit la m??thode en termes de approximations successives x _n ?? la place de la s??quence plus complexe des polyn??mes utilis??s par Newton. Enfin, en 1740, Thomas Simpson d??crit la m??thode de Newton comme une m??thode it??rative pour r??soudre les ??quations non lin??aires g??n??rales en utilisant le calcul fluxional, donnant essentiellement la description ci-dessus. Dans la m??me publication, Simpson donne ??galement la g??n??ralisation des syst??mes de deux ??quations et note que la m??thode de Newton peut ??tre utilis?? pour r??soudre des probl??mes d'optimisation en r??glant le gradient ?? z??ro.

Arthur Cayley en 1879 ?? Le probl??me imaginaire Newton-Fourier a ??t?? le premier qui a remarqu?? les difficult??s ?? g??n??raliser la m??thode de Newton aux racines complexes de polyn??mes de degr?? sup??rieur ?? 2 et complexes valeurs initiales. Cela a ouvert la voie ?? l'??tude de la th??orie d'it??rations de fonctions rationnelles.

Consid??rations pratiques

En g??n??ral convergence quadratique est: l'erreur est essentiellement carr??e ?? chaque ??tape (ce est le nombre de chiffres exacts double ?? chaque ??tape). Il ya quelques mises en garde, cependant. Tout d'abord, la m??thode de Newton n??cessite que le d??riv?? est calcul??e directement. (Si l'instrument d??riv?? est approch??e par le pente d'une droite passant par deux points sur la fonction, la s??cantes r??sultats de la m??thode; cela peut ??tre plus efficace selon la fa??on dont on mesure l'effort de calcul.) Deuxi??mement, si la valeur initiale est trop loin du z??ro absolu, la m??thode de Newton peut ??chouer ?? converger. Pour cette raison, la plupart des impl??mentations pratiques de la m??thode de Newton mis une limite sup??rieure sur le nombre d'it??rations et peut-??tre de la taille des it??ration. Troisi??mement, si le root a recherch?? multiplicit?? sup??rieur ?? un, le taux de convergence ne est que la r??duction des erreurs lin??aires (par un facteur constant ?? chaque ??tape) ?? moins que des mesures sp??ciales soient prises.

Depuis la plus grave des probl??mes ci-dessus est la possibilit?? d'une d??faillance de la convergence, Press et al. (1992) pr??sentent une version de la m??thode de Newton qui commence au point milieu d'un intervalle dans lequel la racine est connue pour se trouver et se arr??te l'it??ration si une it??ration est g??n??r?? qui se trouve en dehors de l'intervalle.

Les d??veloppeurs de syst??mes informatiques ?? grande ??chelle impliquant recherche des racines ont tendance ?? pr??f??rer la Proc??d?? s??cante sur la m??thode de Newton, car l'utilisation d'un quotient de diff??rence ?? la place du d??riv?? de la m??thode de Newton implique que le code suppl??mentaire pour calculer la d??riv??e n'a pas besoin d'??tre maintenue. Dans la pratique, les avantages de maintenir une base de code plus petit emportent g??n??ralement sur les caract??ristiques de convergence sup??rieures de la m??thode de Newton.

Contre-exemples

Les tangentes de x ^ 3-2 x + 2 ?? 0 et une intersection de l'axe-x ?? 1 et 0, respectivement, illustrant pourquoi la m??thode de Newton oscille entre ces valeurs pour quelques points de d??part.

Point de d??part trop loin

Si le point de d??part ne est pas pr??s d'une racine puis la convergence peut ne pas arriver. Laisser

$f (x) = x ^ 3 - 2x + 2 \!$

et de prendre 0 comme point de d??part. La premi??re it??ration produit une seconde et les retours d'it??ration ?? 0 de sorte que la s??quence va osciller entre les deux sans converger ?? une racine. En g??n??ral, le comportement de la s??quence peut ??tre tr??s complexe. (Voir Fractale Newton.)

Dans les exemples suivants, la racine est ?? z??ro souhait??e pour la simplicit??, il aurait pu ??tre plac?? ailleurs.

D??riv??e discontinue

Si le d??riv?? ne est pas continue ?? la racine, puis la convergence peut ??chouer ?? se produire dans ne importe quel quartier de la racine. Consid??rons la fonction

$f (x) = \ begin {} 0 cas et \ mbox {if} x = 0 \\ x + x ^ 2 \ sin (\ frac {2} {x}) & \ mbox {if} x \ neq 0 \ end {} cas$

Puis $f '(0) = 1 \!$ et $f '(x) = 2x + 1 \ sin (2 / x) - 2 \ cos (2 / x) \!$ ailleurs.

Dans ne importe quel quartier de la racine, ce d??riv?? ne cesse de changer signe que x tend vers 0 de la droite (ou ?? partir de la gauche), tandis que $f (x) \ ge x - x ^ 2> 0 \!$ pour $0 <x <1 \!$ .

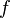Si $f (x) / f '(x) \!$ ne est pas born?? pr??s de la racine et de la m??thode de Newton ne convergera pas, m??me si: la fonction est diff??rentiable partout; le d??riv?? ne est pas nulle ?? la racine; $f \!$ est infiniment d??rivable sauf ?? la racine; et le d??riv?? est d??limit?? au voisinage de la racine (contrairement ?? son inverse).

Aucune d??riv??e seconde

Si il ne est pas d??riv??e seconde ?? la racine, puis la convergence peut manquer d'??tre quadratique. En effet, soit

$f (x) = x + x ^ {4/3} \!$

Puis

$f '(x) = 1 + (03/04) x ^ {1/3} \!$

$f '' (x) = (4/9) x ^ {- 3.2} \!$

except?? quand $x = 0 \!$ o?? il ne est pas d??finie. Donn?? $x_n \!$ ,

$x_ {n + 1} = x_n - \ frac {f (xn)} {f '(xn)} = \ frac {(1/3) x_n ^ {4/3}} {(1 + (4/3) x_n ^ {1/3})} \!$

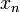qui a environ 4/3 fois plus de bits de pr??cision que 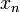$x_n \!$ a. Ce est moins que les deux fois plus nombreux qui seraient n??cessaires pour la convergence quadratique. Donc, la convergence de la m??thode de Newton (dans ce cas) ne est pas quadratique, m??me si: la fonction est contin??ment diff??rentiable partout; le d??riv?? ne est pas nulle ?? la racine; et 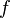$f \!$ est infiniment d??rivable sauf ?? la racine souhait??e.

D??riv??e nulle

Si le premier d??riv?? est ??gal ?? z??ro ?? la racine, puis convergence ne sera pas quadratique. En effet, soit

$f (x) = x ^ 2 \!$

Puis $f '(x) = 2x \!$ et par cons??quent $x - f (x) / f '(x) = x / 2 \!$ . Donc, la convergence ne est pas quadratique, m??me si la fonction est infiniment diff??rentiable partout.

Analyse

Supposons que la fonction f a une α ?? z??ro, ce est-f (α) = 0.

Si f est contin??ment diff??rentiable et son d??riv?? ne annule pas en α, alors il existe une voisinage de α tel que, pour toutes les valeurs de d??part x ₀ dans ce quartier, la s??quence {x _n} sera converge vers α.

Si la fonction est contin??ment diff??rentiable et son d??riv?? ne annule pas en α et il a une d??riv??e seconde α puis la convergence est quadratique ou plus rapide. Si la d??riv??e seconde ne annule pas en α puis la convergence est simplement quadratique.

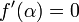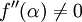Si le d??riv?? ne dispara??t au α, alors la convergence ne est g??n??ralement lin??aire. Plus pr??cis??ment, si f est deux fois contin??ment diff??rentiable, $f '(\ alpha) = 0 \!$ et $f '' (\ alpha) \ ne 0 \!$ , Alors il existe un voisinage de α tel que, pour toutes les valeurs de d??part x ₀ dans ce quartier, la s??quence d'it??ration converge lin??airement, avec journal des taux _{de 10} 2 (S??li & Mayers, l'exercice 1.6). 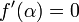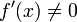Alternativement, si $f '(\ alpha) = 0 \!$ et $f '(x) \ ne 0 \!$ ailleurs, dans un voisinage U de α, α ??tant un z??ro de r multiplicit?? et si 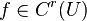$f \ in C ^ r (U)$ alors il existe un voisinage de α tel que, pour toutes les valeurs de d??part x ₀ dans ce quartier, la s??quence d'it??ration converge lin??airement.

Cependant, m??me la convergence lin??aire ne est pas garantie dans des situations pathologiques.

En pratique, ces r??sultats sont local et le quartier de convergence ne sont pas connus a priori, mais il ya aussi des r??sultats sur la convergence mondiale, par exemple, ??tant donn?? un quartier droit U ₊ de α, si f est deux fois d??rivable dans U ₊ et si 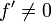$f '\ ne 0 \!$ , $f \ cdot f ''> 0 \!$ ?? U _+, puis, pour chaque x _{0 +} U dans la s??quence x _k est monotone d??croissante de α.

G??n??ralisations

Syst??mes d'??quations non lin??aires

On peut utiliser la m??thode de Newton aussi pour r??soudre des syst??mes de k (non lin??aires) ??quations, ce qui revient ?? trouver les z??ros de fonctions contin??ment d??rivables F: R ^k → R ^k. Dans la formulation indiqu??e ci-dessus, on a alors laiss?? ?? multiplier par l'inverse de la k k -by- Jacobienne matrice J _F (x _n) au lieu de diviser par f '(x _n). Plut??t que de calcul fait l'inverse de cette matrice, on peut gagner du temps en r??solvant le syst??me d'??quations lin??aires

$J_F (xn) (x_ {n + 1} - x_n) = -F (xn) \, \!$

pour l'inconnu x _{n 1} - x _n. Encore une fois, cette m??thode ne fonctionne que si la valeur initiale x ₀ est suffisamment proche de la vraie z??ro. Typiquement, une r??gion qui est bien ??lev?? est situ?? d'abord avec une autre m??thode et la m??thode de Newton est ensuite utilis?? pour "polish" une racine qui est d??j?? connu environ.

??quations non lin??aires dans un espace de Banach

Une autre g??n??ralisation est la m??thode de Newton pour trouver un z??ro d'une fonction F d??finie dans un Espace de Banach. Dans ce cas, la formulation est

$X_ {n + 1} = X_n- (F '_ {} X_n) ^ {- 1} [F (X_n)]$ ,

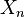o?? $F '_ {} X_n$ est le Fr??chet appliqu?? au point $X_n$ . Il faut le d??riv?? Fr??chet ??tre inversible ?? chaque 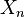$X_n$ pour que la m??thode soit applicable.

Fonctions complexes

Bassins d'attraction pour x ^5-1 = 0; fonc??e signifie plus d'it??rations pour converger.

Lorsqu'il se agit de fonctions complexes, toutefois, la m??thode de Newton peuvent ??tre appliqu??s directement ?? trouver leurs z??ros. Pendant de nombreuses fonctions complexes, la limite de l'ensemble (??galement connu sous le nom bassin d'attraction) ?? partir de toutes les valeurs qui provoquent le proc??d?? de converger vers z??ro un particulier est une fractale .

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Newton%27s_method&oldid=203256519 "