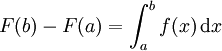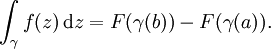Th??or??me fondamental du calcul
Renseignements g??n??raux
Cette s??lection ??coles a ??t?? choisi par SOS Enfants pour les ??coles dans le monde en d??veloppement ne ont pas acc??s ?? Internet. Il est disponible en t??l??chargement intranet. SOS Children travaille dans 45 pays africains; pouvez-vous aider un enfant en Afrique ?
Le th??or??me fondamental du calcul pr??cise la relation entre les deux op??rations centrales de calcul , la diff??renciation et l'int??gration .
La premi??re partie du th??or??me, parfois appel?? le premier th??or??me fondamental du calcul, montre qu'un l'int??gration ind??termin??e peut ??tre invers??e par une diff??renciation.
La deuxi??me partie, parfois appel?? le deuxi??me th??or??me fondamental du calcul, permet de calculer l' int??grale d??finie d'une fonction ?? l'aide de l'un de ses infinit?? primitives. Cette partie du th??or??me a des applications pratiques pr??cieux, car il simplifie consid??rablement le calcul des int??grales d??finies.
La premi??re d??claration publi??e et la preuve d'une version restreinte du th??or??me fondamental ??tait par James Gregory (1638-1675). Isaac Barrow se est av??r?? la premi??re version compl??tement g??n??rale du th??or??me, tout en ??tudiant de Barrow Isaac Newton (1643-1727) a compl??t?? le d??veloppement de la th??orie math??matique environnante. Gottfried Leibniz (1646-1716) a syst??matis?? la connaissance dans un calcul des quantit??s infinit??simales.
Intuition
Intuitivement, le th??or??me affirme simplement que la somme de modifications infinit??simales dans une quantit?? au fil du temps (ou une autre quantit??) se ajoutent ?? la variation nette de la quantit??.
Pour comprendre cette d??claration, nous allons commencer avec un exemple. Supposons une particule se d??place en ligne droite avec sa position donn??e par x (t) o?? t est le temps et x (t) signifie que x est une fonction de t. Le d??riv?? de cette fonction est ??gale ?? la variation en quantit?? infinit??simale, d x, par changement infime dans le temps, d t (bien s??r, le d??riv?? lui-m??me d??pend du temps). D??finissons ce changement dans la distance par changement dans le temps que la vitesse v de la particule. En Notation de Leibniz:
R??organisation de cette ??quation, il se ensuit que:
Par la logique ci-dessus, un changement de x ( 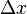 ) Est la somme des changements infinit??simaux d x. Il est ??galement ??gale ?? la somme des produits infinit??simales du d??riv?? et du temps. Cette sommation infinie est l'int??gration; par cons??quent, l'op??ration d'int??gration permet la r??cup??ration de la fonction d'origine ?? partir de son d??riv??. Comme on peut raisonnablement d??duire, cette op??ration fonctionne en sens inverse que nous pouvons diff??rencier le r??sultat de notre int??grante de r??cup??rer le d??riv?? d'origine.
) Est la somme des changements infinit??simaux d x. Il est ??galement ??gale ?? la somme des produits infinit??simales du d??riv?? et du temps. Cette sommation infinie est l'int??gration; par cons??quent, l'op??ration d'int??gration permet la r??cup??ration de la fonction d'origine ?? partir de son d??riv??. Comme on peut raisonnablement d??duire, cette op??ration fonctionne en sens inverse que nous pouvons diff??rencier le r??sultat de notre int??grante de r??cup??rer le d??riv?? d'origine.
D??clarations officielles
Il ya deux parties au th??or??me fondamental du calcul. Librement mis, la premi??re partie traite de la d??riv?? d'un primitive, tandis que les deuxi??me partie traite de la relation entre primitives et int??grales d??finies .
Premi??re partie
Cette partie est parfois appel??e Premi??re th??or??me fondamental du calcul.
Soit f une fonction num??rique continue d??finie sur un intervalle ferm?? [a, b]. Soit F la fonction d??finie, pour tout x dans [a, b], par
Puis, F est d??rivable sur [a, b], et pour tout x dans [a, b],
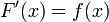 .
.
L'op??ration 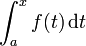 est une int??grale d??finie par la limite sup??rieure variable et son r??sultat F (x) est l'un des nombreux infiniment primitives de f.
est une int??grale d??finie par la limite sup??rieure variable et son r??sultat F (x) est l'un des nombreux infiniment primitives de f.
Deuxi??me partie
Cette partie est parfois appel??e Deuxi??me th??or??me fondamental du calcul.
Soit f une fonction num??rique continue d??finie sur un intervalle ferm?? [a, b]. Soit F une primitive de f, ce est l'un des infiniment nombreuses fonctions telles que, pour tout x dans [a, b],
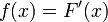 .
.
Puis
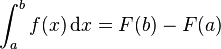 .
.
Corollaire
Soit f une fonction r??elle d??finie sur un intervalle ferm?? [a, b]. Soit F une fonction telle que, pour tout x dans [a, b],
Alors, pour tout x dans [a, b],
et
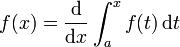 .
.
Exemples
A titre d'exemple, supposons que vous devez calculer
Ici, 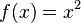 et nous pouvons utiliser
et nous pouvons utiliser 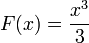 que la primitive. Par cons??quent:
que la primitive. Par cons??quent:
Ou, plus g??n??ralement, supposons que vous devez calculer
Ici, 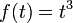 et nous pouvons utiliser
et nous pouvons utiliser 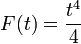 que la primitive. Par cons??quent:
que la primitive. Par cons??quent:
Mais ce r??sultat aurait pu ??tre trouv?? beaucoup plus facilement que
Preuve
Supposer que
Soit deux nombres x 1 et x 1 + Δ x dans [a, b]. Donc, nous avons
et
En soustrayant les deux ??quations donne
On peut montrer que
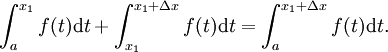
- (La somme des aires des deux r??gions adjacentes est ??gale ?? la zone des deux r??gions combin??es.)
Manipuler cette ??quation donne
La substitution de ce qui pr??c??de (1) entra??ne
Selon le signifie th??or??me de la valeur d'int??gration, il existe un en c [x 1, x 1 + Δ x] tels que
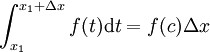 .
.
La substitution de ce qui pr??c??de (2) nous obtenons
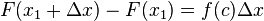 .
.
Divisant les deux c??t??s par Δ x donne
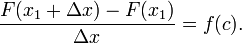
- Notez que l'expression sur le c??t?? gauche de l'??quation est Newton diff??rence quotient F en x 1.
Prenez la limite que Δ x → 0 des deux c??t??s de l'??quation.
L'expression sur le c??t?? gauche de l'??quation est la d??finition de la d??riv??e de F ?? 1 x.
Pour trouver l'autre limite, nous allons utiliser la Th??or??me des gendarmes. Le nombre c est dans l'intervalle [x 1, x 1 + Δ x], de sorte que x 1 ≤ c ≤ x 1 + Δ x.
Aussi, 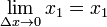 et
et 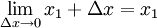 .
.
Par cons??quent, d'apr??s le th??or??me de compression,
Substituant dans (3), nous obtenons
La fonction f est continue en c, de sorte que la limite peut ??tre prise ?? l'int??rieur de la fonction. Par cons??quent, on obtient
 .
.
qui compl??te la preuve.
(Leithold et al, 1996)
Preuve alternative
Ce est une limite par la preuve Riemann r??sume.
Soit f continue sur l'intervalle [a, b], et soit F une primitive de f. Commencez par la quantit??
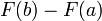 .
.
Qu'il y ait des num??ros
- x 1, ..., x n
tel que
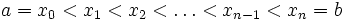 .
.
Il se ensuit que
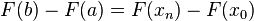 .
.
Maintenant, nous ajoutons chaque F (x i) avec son inverse additif, de sorte que la quantit?? r??sultante est ??gale:
La quantit?? ci-dessus peut ??tre ??crite comme la somme suivante:
Ensuite, nous allons utiliser le valeur moyenne th??or??me. En r??sum??,
Soit F continue sur l'intervalle ferm?? [a, b] et d??rivable sur l'intervalle ouvert (a, b). Ensuite, il existe un c dans (a, b) de telle sorte que
Il se ensuit que
La fonction F est d??rivable sur l'intervalle [a, b]; par cons??quent, il est ??galement diff??rentiable et continue sur chaque intervalle x i -1. Par cons??quent, selon le th??or??me de la valeur moyenne (ci-dessus),
La substitution de ce qui pr??c??de (1), on obtient
L'hypoth??se implique  Aussi,
Aussi,  peut ??tre exprim??e comme
peut ??tre exprim??e comme 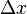 de la partition
de la partition  .
.

Notez que nous d??crivons l'aire d'un rectangle, avec les temps de largeur la hauteur, et nous ajoutons les r??gions ensemble. Chaque rectangle, en vertu de la Valeur moyenne th??or??me, d??crit une approximation de la section de la courbe est tir??e par dessus. Notez ??galement que 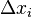 n'a pas besoin d'??tre le m??me pour toute valeur de
n'a pas besoin d'??tre le m??me pour toute valeur de  Ou en d'autres termes que la largeur des rectangles peuvent diff??rer. Ce que nous avons ?? faire est de rapprocher la courbe avec
Ou en d'autres termes que la largeur des rectangles peuvent diff??rer. Ce que nous avons ?? faire est de rapprocher la courbe avec  rectangles. Maintenant, comme la taille des partitions obtenir plus petits et n augmente, r??sultant en plusieurs partitions pour couvrir l'espace, nous allons nous rapprocher et plus proche de la superficie r??elle de la courbe.
rectangles. Maintenant, comme la taille des partitions obtenir plus petits et n augmente, r??sultant en plusieurs partitions pour couvrir l'espace, nous allons nous rapprocher et plus proche de la superficie r??elle de la courbe.
En prenant la limite de l'expression comme la norme des partitions se rapproche de z??ro, nous arrivons ?? la Int??grale de Riemann. Ce est, nous prenons la limite comme le plus grand des partitions tend vers z??ro dans la taille, de sorte que toutes les autres partitions sont plus petits et le nombre de partitions tend vers l'infini.
Ainsi, on prend la limite des deux c??t??s de (2). Cela nous donne
Ni F (b) ni F (a) d??pend || Δ ||, de sorte que la limite sur le c??t?? gauche reste F (b) - f (a).
L'expression sur le c??t?? droit de l'??quation d??finit une int??grale sur f de a ?? b. Par cons??quent, on obtient
qui compl??te la preuve.
G??n??ralisations
Nous ne avons pas besoin d'assumer la continuit?? de f sur tout l'intervalle. Partie I du th??or??me dit alors: si f est toute int??grable Lebesgue fonction sur [a, b] et x 0 est un nombre dans [a, b] tel que f est continue en x 0,
est d??rivable pour x = x 0 ?? F '(x 0) = f (x 0). Nous pouvons assouplir les conditions sur f encore et supposons que ce est simplement localement int??grable. Dans ce cas, nous pouvons conclure que la fonction F est diff??rentiable '(x) = presque partout et F f (x) presque partout. Ce est parfois connu comme la diff??renciation du th??or??me de Lebesgue.
Partie II du th??or??me est vrai pour toute fonction int??grable Lebesgue f qui a une primitive F (fonctions int??grables font pas tous, cependant).
La version du Th??or??me de Taylor qui exprime le terme d'erreur comme une int??grale peut ??tre consid??r??e comme une g??n??ralisation du th??or??me fondamental.
Il existe une version du th??or??me de complexes fonctions: supposons U est un ouvert de C et f: U → C est une fonction qui a une F primitive holomorphe sur U. Ensuite, pour chaque courbe γ: [a, b] → U, le courbe int??grale peut ??tre calcul??e comme
Le th??or??me fondamental peut ??tre g??n??ralis??e ?? courbes et de surfaces int??grales de dimensions sup??rieures et collecteurs .
L'une des d??clarations les plus puissants dans cette direction est Th??or??me de Stokes.
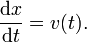
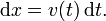
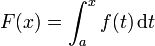
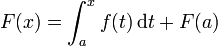
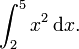

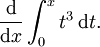
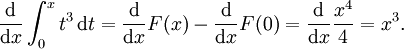

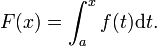
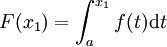
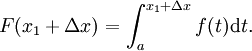
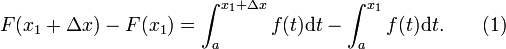
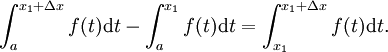
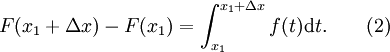
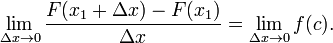
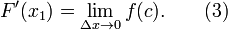
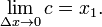
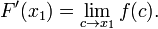
![\ Begin {matrix} F (b) - F (a) & = & F (xn) \, + \, [- F (x_ {n-1}) \, + \, F (x_ {n-1} )] \, + \, \ ldots \, + \, [- F (x 1) + F (x 1)] \, - \, F (x_0) \, \\ & = & [F (xn) \, - \, F (x_ {n-1})] \, + \, [F (x_ {n-1}) \, + \, \ ldots \, - \, F (x 1)] \, + \, [ F (x 1) \, - \, F (x_0)] \, \ end {matrix}](../../images/62/6206.png)
![F (b) - F (a) = \ sum_ {i = 1} ^ n [F (x_i) - F (x_ {i-1})] \ qquad (1)](../../images/62/6207.png)

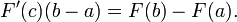
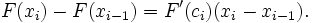
![F (b) - F (a) = \ sum_ {i = 1} ^ n [F '(c_i) (x_i - x_ {i-1})].](../../images/62/6211.png)
![F (b) - F (a) = \ sum_ {i = 1} ^ n [f (c_i) (\ Delta x_i)] \ qquad (2)](../../images/62/6215.png)
![\ Lim _ {\ | \ Delta \ | \ 0} F (b) - F (a) = \ lim _ {\ | \ Delta \ | \ 0} \ sum_ {i = 1} ^ n [f (c_i) (\ Delta x_i)] \ ,.](../../images/62/6225.png)
![F (b) - F (a) = \ lim _ {\ | \ Delta \ | \ 0} \ sum_ {i = 1} ^ n [f (c_i) (\ Delta x_i)]](../../images/62/6226.png)