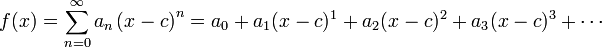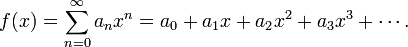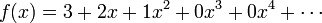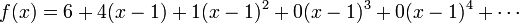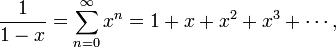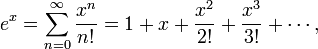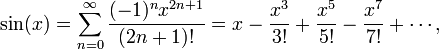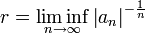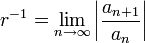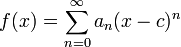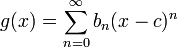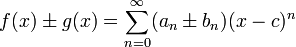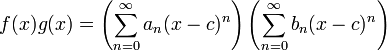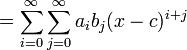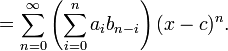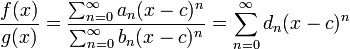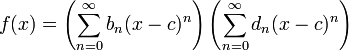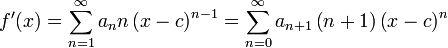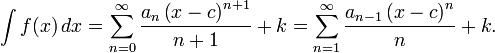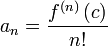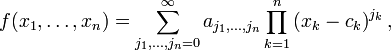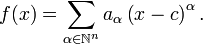s??rie Power

Contexte des ??coles Wikip??dia

Cette s??lection Wikipedia est d??connect?? disponibles ?? partir enfants SOS pour la distribution dans le monde en d??veloppement. Une bonne fa??on d'aider d'autres enfants est de parrainer un enfant

En math??matiques , une s??rie de puissance (une variable) est un s??rie infinie de la forme

$f (x) = \ sum_ {n = 0} ^ \ infty a_n \ left (xc \ right) ^ n = a_0 + a_1 (xc) ^ 1 + a_2 (xc) ^ 2 + A_3 (xc) ^ 3 + \ cdots$

o?? _n repr??sente un coefficient correspondant ?? la n i??me terme, c est une constante, et x varie autour de c (pour cette raison, on parle parfois de la s??rie comme ??tant centr??e ?? c). Cette s??rie se pose g??n??ralement que la s??rie de Taylor de certains connu fonction ; la s??rie de Taylor article contient de nombreux exemples.

Dans de nombreuses situations, c est ??gal ?? z??ro, par exemple lors de l'examen d'une s??rie de Maclaurin . Dans de tels cas, la s??rie de puissance prend la forme simple

$f (x) = \ sum_ {n = 0} ^ \ infty A_N x ^ n = a_0 + x + A_1 A_2 x ^ 2 + A_3 x ^ 3 + \ cdots.$

Ces s??ries de puissance proviennent principalement de l'analyse, mais ??galement se produire dans la combinatoire (sous le nom de g??n??rer fonctions) et en g??nie ??lectrique (sous le nom de la Z-transform). Le familier notation d??cimale pour entiers peut aussi ??tre consid??r??e comme un exemple d'une s??rie de puissance, mais avec l'argument x fix?? ?? 10. En th??orie des nombres , la notion de nombres p-adiques est aussi ??troitement li??e ?? celle d'une s??rie de puissance.

La fonction exponentielle (en bleu), et la somme des n premiers termes de son une s??rie de puissance Maclaurin (en rouge).

Exemples

Tout polyn??me peut ??tre facilement exprim??e comme une s??rie d'alimentation autour de ne importe quel centre c, quoique avec la plupart des coefficients ??gaux ?? z??ro. Par exemple, le polyn??me 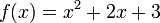$f (x) = x ^ 2 + 2x + 3$ peut se ??crire comme une s??rie de puissance autour du centre 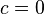$c = 0$ comme

$f (x) = x 3 + 2 + 1 x ^ 2 + 0 x ^ 3 + 0 + x ^ 4 \ cdots \,$

ou autour du centre 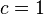$c = 1$ comme

$f (x) = 6 + 4 (x-1) + 1 (x-1) ^ 2 + 0 (x-1) + 3 ^ 0 (x-1) + 4 ^ \ cdots \,$

ou encore autour de tout autre centre c. On peut voir la s??rie de puissance comme ??tant comme "polyn??mes de degr?? infini,?? bien que la s??rie de puissance ne sont pas polyn??mes.

Le formule s??rie g??om??trique

$\ frac {1} {1} = x-\ sum_ {n = 0} ^ \ infty x ^ n = 1 + x + x ^ 2 + x ^ 3 + \ cdots,$

qui est valable pour 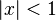$| X | <1$ , Est un des exemples les plus importants d'une s??rie de puissance, ainsi que la formule de fonction exponentielle

$e ^ x = \ sum_ {n = 0} ^ \ infty \ frac {x ^ n} {n!} = 1 + x + \ frac {x ^ 2} {2!} + \ frac {x ^ 3} { 3!} + \ cdots,$

et la formule sine

$\ Sin (x) = \ sum_ {n = 0} ^ \ infty \ frac {(- 1) ^ nx ^ {2n + 1}} {(2n + 1)!} = X - \ frac {x ^ 3} {3!} + \ frac {x ^ 5} {5!} - \ frac {x ^ 7} {!} + 7 \ cdots,$

valable pour tout r??el x. Ces s??ries de puissance sont aussi des exemples de s??ries de Taylor .

Puissances n??gatives ne sont pas autoris??es dans une s??rie de puissance, par exemple 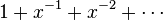$1 + x ^ {- 1} + x ^ {- 2} + \ cdots$ ne est pas consid??r??e comme une s??rie de puissance (bien que ce soit un Laurent s??rie). Pouvoirs m??me, fractionnaires tels que 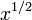$x ^ {1/2}$ ne sont pas autoris??s (mais voir Puiseux s??rie). Les coefficients 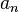$a_n$ ne sont pas autoris??s ?? d??pendre $x$ , Ainsi, par exemple:

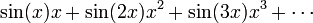$\ Sin (x) + x \ sin (2x) x ^ 2 + \ sin (3x) x ^ 3 + \ cdots \,$ ne est pas une s??rie de puissances.

Rayon de convergence

Une s??rie de puissance vont converger pour certaines valeurs de la variable x et peuvent se ??carter pour d'autres. Toutes les s??ries de puissance converge ?? x = c. Il ya toujours un nombre r avec 0 ≤ r ≤ ∞ tels que la s??rie converge lorsque | x - c | <r et diverge lorsque | x - c |> r. Le nombre r est appel?? le rayon de convergence de la s??rie de puissance; en g??n??ral, elle est donn??e ?? titre

$r = \ liminf_ {n \ to \ infty} \ left | a_n \ right | ^ {- \ frac {1} {n}}$

ou, de mani??re ??quivalente,

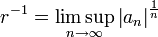
$r ^ {- 1} = \ limsup_ {n \ to \ infty} \ left | a_n \ right | ^ {\ frac {1} {n}}$

(Voir Limites inf??rieure et sup??rieure). Un moyen rapide pour calculer ce est

$r ^ {- 1} = \ lim_ {n \ to \ infty} \ left | {a_ {n + 1} \ over a_n} \ right |$

si cette limite existe.

Les s??ries converge absolument | x - c | <r et converge uniform??ment sur tout compacte sous-ensemble de {x: | x - c | <r}.

Pour | x - c | = r, nous ne pouvons faire aucune d??claration g??n??rale si la s??rie converge ou diverge. Cependant, Le th??or??me d'Abel indique que la somme de la s??rie est continue au point x si la s??rie converge ?? x.

Les op??rations sur les s??ries de puissance

Addition et soustraction

Lorsque sont d??compos??s deux fonctions f et g dans la s??rie de puissance autour du m??me centre C, la s??rie de puissances de la somme ou la diff??rence des fonctions peuvent ??tre obtenues par addition et la soustraction de termwise. Autrement dit, si:

$f (x) = \ sum_ {n = 0} ^ \ infty a_n (x-c) ^ n$

$g (x) = \ sum_ {n = 0} ^ \ infty b_n (x-c) ^ n$

puis

$f (x) \ h g (x) = \ sum_ {n = 0} ^ \ infty (a_n \ h b_n) (xc) ^ n$

Multiplication et division

Avec les m??mes d??finitions ci-dessus, pour la s??rie d'alimentation du produit et quotient des fonctions peuvent ??tre obtenus comme suit:

$f (x) g (x) = \ left (\ sum_ {n = 0} ^ \ infty a_n (xc) ^ n \ right) \ left (\ sum_ {n = 0} ^ \ infty b_n (xc) ^ n \ right)$

$= \ Sum_ {i = 0} ^ \ infty \ sum_ {j = 0} ^ \ infty a_i b_j (xc) ^ {i + j}$

$= \ Sum_ {n = 0} ^ \ infty \ gauche (\ sum_ {i = 0} ^ n a_i b_ {ni} \ right) (xc) ^ n.$

La s??quence 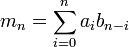$m_n = \ sum_ {i = 0} ^ n a_i b_ {n-i}$ qui est connu comme le convolution de la s??quence 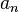$a_n$ et $b_n$ .

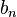Pour la division, d'observer:

${F (x) \ over g (x) = {} \ sum_ {n = 0} ^ \ infty a_n (xc) ^ n \ over \ sum_ {n = 0} ^ \ infty b_n (xc) ^ n} = \ sum_ {n = 0} ^ \ infty d_n (xc) ^ n$

$f (x) = \ left (\ sum_ {n = 0} ^ \ infty b_n (xc) ^ n \ right) \ left (\ sum_ {n = 0} ^ \ infty d_n (xc) ^ n \ right)$

puis utiliser ce qui pr??c??de, la comparaison des coefficients.

Diff??renciation et d'int??gration

Une fois qu'une fonction est donn??e ?? une s??rie de puissance, il est continue l?? o?? il converge et est d??rivable sur la int??rieur de cet ensemble. Il peut ??tre diff??renci?? et int??gr?? assez facilement, en traitant s??par??ment chaque terme:

$f ^ \ prime (x) = \ sum_ {n = 1} ^ \ infty a_n n \ gauche (xc \ right) ^ {n-1} = \ sum_ {n = 0} ^ \ infty a_ {n + 1} \ left (n + 1 \ right) \ left (xc \ right) ^ {n}$

$\ Int f (x) \, dx = \ sum_ {n = 0} ^ \ infty \ frac {a_n \ gauche (xc \ right) ^ {n + 1}} {n + 1} + k = \ {n sum_ = 1} ^ \ infty \ frac {a_ {n-1} \ left (xc \ right) ^ {n}} {} n + k.$

Ces deux s??ries ont le m??me rayon de convergence que celui d'origine.

Fonctions analytiques

Une fonction f d??finie sur certaines ouvert U de R ou C est appel?? analytique si elle est localement donn??e par la s??rie de puissance. Cela signifie que tout a ∈ U a un ouverte voisinage V ⊆ U, tel qu'il existe une s??rie de puissance de centre a qui converge vers f (x) pour tout x ∈ V.

Chaque s??rie de puissance avec un rayon positif de la convergence est analytique sur la int??rieur de sa r??gion de convergence. Tous fonctions holomorphes sont analytique complexe. Les sommes et produits de fonctions analytiques sont analytiques, comme le sont les quotients tant que le d??nominateur est diff??rent de z??ro.

Si une fonction est analytique, il est infiniment souvent diff??rentiables, mais dans le cas r??el l'inverse ne est pas vrai en g??n??ral. Pour une fonction analytique, les coefficients a _n peut ??tre calcul?? comme

$a_n = \ frac {f ^ {\ left (n \ right)} \ left (c \ right)} {n!}$

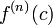o?? $^ {f (n)} (c)$ d??signe la ni??me d??riv??e de f au c, et 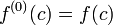$f ^ {(0)} (c) = f (c)$ . Cela signifie que chaque fonction analytique est repr??sent?? localement par son s??rie de Taylor .

La forme globale d'une fonction analytique est compl??tement d??termin??e par son comportement local dans le sens suivant: si f et g sont deux fonctions analytiques d??finies sur le m??me ouvert connexe U, et se il existe un ??l??ment c ∈ U tel que f ⁽ⁿ⁾ (c) = g ⁽ⁿ⁾ (c) pour tout n ≥ 0, alors f (x) = g (x) pour tout x ∈ U.

Si une s??rie de puissance avec un rayon de convergence R est donn??, on peut consid??rer continuations analytiques de la s??rie, ce est ?? dire les fonctions analytiques f qui sont d??finis sur de plus grands ensembles de {x: | x - c | <r} et d'accord avec la s??rie de puissance donn??e sur cet ensemble. Le nombre r est maximale dans le sens suivant: il existe toujours un nombre complexe x avec | x - a | = r de telle sorte qu'aucun prolongement analytique de la s??rie peut ??tre d??fini en x.

Le d??veloppement en s??rie de puissance de la fonction inverse d'une fonction analytique peut ??tre d??termin??e en utilisant le Lagrange th??or??me d'inversion.

Les s??ries formelles

En alg??bre abstraite , on tente de capturer l'essence de la s??rie de puissance sans ??tre limit?? ?? la champs de nombres r??els et complexes, et sans le besoin de parler de convergence. Cela conduit ?? la notion de s??rie formelle, un concept d'une grande utilit?? dans combinatoire alg??brique.

s??rie Power ?? plusieurs variables

Une extension de la th??orie est n??cessaire aux fins de Fonction de plusieurs variables. Une s??rie de puissance est ici d??fini comme une s??rie infinie de la forme

$f (x 1, \ dots, x_n) = \ {sum_ j_1, \ dots, j_n = 0} ^ {\ infty} {a_ j_1, \ dots, j_n} \ prod_ {k = 1} ^ n \ gauche (x_k - C_K \ right) ^ {} j_k,$

o?? j = (j _1, ..., _n j) est un vecteur de nombres entiers, les coefficients a _{(j 1, ..., n j)} sont g??n??ralement des nombres r??els ou complexes, et le centre c = (c ₁ , ..., c _n) et l'argument x = (x _1, ..., x _n) sont g??n??ralement des vecteurs r??els ou complexes. Dans la plus pratique Multi-indice ce qui peut ??tre ??crit

$f (x) = \ sum _ {\ alpha \ in \ mathbb {N} ^ n} a _ {\ alpha} \ left (x - c \ right) ^ {\ alpha}.$

La th??orie de cette s??rie est plus difficile que pour les s??ries une seule variable, avec des zones les plus complexes de convergence. Par exemple, la s??rie de puissance 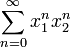$\ Sum_ {n = 0} ^ \ infty x_1 ^ n ^ n x_2$ est absolument convergente dans l'ensemble 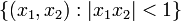$\ {(X_1, x_2): | x_1 x_2 | <1 \}$ entre deux hyperboles. (Ceci est un exemple d'un ensemble de connexion convexe, en ce sens que l'ensemble des points 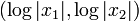$(\ Log | x_1 |, \ log | x_2 |)$ O?? 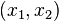$(X_1, x_2)$ se trouve dans la r??gion ci-dessus, est un ensemble convexe. Plus g??n??ralement, on peut montrer que lorsque c = 0, l'int??rieur de la r??gion de la convergence absolue est toujours un ensemble de log-convexe dans ce sens.) D'autre part, ?? l'int??rieur de cette r??gion de la convergence, on peut diff??rencier et int??grer sous le signe de la s??rie, tout comme on peut avec des s??ries de pouvoir ordinaire.

Ordre d'une s??rie de puissance

Soit α ??tre un multi-index pour une s??rie de f de puissance (x _1, x _2, ..., x _n). L'ordre de la s??rie de puissance f est d??fini comme ??tant le moins de valeur | α | tels que _α ≠ 0, ou 0 si f ≡ 0. En particulier, pour une s??rie de puissance f (x) dans une seule variable x, l'ordre f est de la plus petite puissance de x par un coefficient diff??rent de z??ro. Cette d??finition se ??tend facilement ?? la Laurent s??rie.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Power_series&oldid=201226722 "