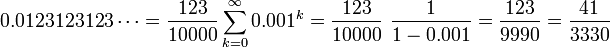D??cimal
?? propos de ce ??coles s??lection Wikipedia
Cette s??lection ??coles a ??t?? choisi par SOS Enfants pour les ??coles dans le monde en d??veloppement ne ont pas acc??s ?? Internet. Il est disponible en t??l??chargement intranet. SOS Enfants a regard?? des enfants en Afrique depuis quarante ans. Pouvez-vous aider dans leur travail en Afrique ?
| Syst??mes de num??ration par la culture |
|---|
|
| Syst??mes de positionnement par base |
| Decimal (10) |
| Ternaire ??quilibr?? |
| Liste des syst??mes de num??ration |
Le d??cimal (base dix ou occasionnellement denier) syst??me num??rique a comme dix base. Ce est le syst??me num??rique le plus largement utilis??, peut-??tre parce que les humains ont quatre les doigts et le pouce de chaque main, ce qui donne un total de dix chiffres plus de deux mains.
Notation d??cimale
Notation d??cimale est l'??criture de nombres dans la base de dix- syst??me num??rique , qui utilise diff??rents symboles (appel??s chiffres ) pour pas plus de dix valeurs distinctes (0, 1, 2, 3, 4, 5, 6, 7, 8 et 9 ) pour repr??senter des chiffres, peu importe la taille. Ces chiffres sont souvent utilis??s avec un s??parateur d??cimal qui indique le d??but d'une partie fractionnaire, et l'un des symboles + (positive) ou de signe - (n??gatifs) en face des chiffres pour indiquer signe. Il n'y a que deux syst??mes de d??cimales vraiment de position dans la civilisation antique, le Chinoise syst??me de tiges de comptage et le syst??me num??rique hindou-arabe, les deux ne ont pas n??cessit?? plus de dix symboles. Autres syst??mes num??riques n??cessitent plus ou moins de symboles.
Le est un syst??me d??cimal Syst??me num??rique de position; il a des positions pour des unit??s, dizaines, centaines, etc. La position de chaque chiffre transmet le multiplicateur (une puissance de dix) pour ??tre utilis?? avec ce chiffre-chaque position a une valeur dix fois sup??rieure ?? celle de la position ?? sa droite.
Dix est le nombre qui est le nombre de doigts et les pouces sur les deux mains (ou les orteils sur les pieds). Dans de nombreuses langues, le mot chiffres ou sa traduction est aussi le terme anatomique faisant r??f??rence ?? doigts et les orteils. En anglais, d??cimal (decimus < Lat. ) signifie dixi??me, d??cimer des moyens de r??duire d'un dixi??me, et denier (denier <lat.) d??signe la Unit?? de dix. Les symboles pour les chiffres d'usage courant dans le monde aujourd'hui sont appel??s Chiffres arabes par les Europ??ens et Chiffres indiens par les Arabes, les termes des deux groupes ?? la fois r??f??rence ?? la culture ?? partir de laquelle ils ont appris le syst??me. Cependant, les symboles utilis??s dans diff??rentes zones ne sont pas identiques; par exemple, les chiffres arabes occidentaux (?? partir de laquelle les chiffres europ??ens sont d??riv??s) diff??rent des formes utilis??es par d'autres cultures arabes.
Notations alternatifs
Certaines cultures ne, ou utilis??s pour, utiliser d'autres syst??mes de num??ration, y compris pr??colombienne Cultures m??so-am??ricaines comme le Maya, qui utilisent un syst??me vig??simal (en utilisant tous les vingt doigts et orteils), certains Nig??rians qui utilisent plusieurs duodecimal (base 12) syst??mes, les Babyloniens , qui a utilis?? sexag??simal (base 60), et de la Yuki, qui aurait utilis?? octal (base 8).
Informatique mat??riel et des syst??mes logiciels utilisent couramment une repr??sentation binaire , en interne. Pour usage externe par des sp??cialistes informatiques, cette repr??sentation binaire est parfois pr??sent??e dans le connexes octaux ou hexad??cimaux syst??mes. Pour la plupart des applications, cependant, les valeurs binaires sont converties en valeurs d??cimales ??quivalentes pour la pr??sentation et la manipulation par l'homme.
Les deux ordinateurs et de logiciels utilisent ??galement des repr??sentations internes qui sont effectivement d??cimales pour stocker des valeurs d??cimales et faire de l'arithm??tique. Souvent cette arithm??tique est effectu?? sur les donn??es qui sont cod??es ?? l'aide cod?? en binaire d??cimal, mais il ya d'autres repr??sentations d??cimales en usage (voir IEEE 754r), en particulier dans les impl??mentations de bases de donn??es. Arithm??tique d??cimale est utilis?? dans les ordinateurs afin que les r??sultats des fractions d??cimales peuvent ??tre calcul??es exactement, qui ne est pas possible en utilisant une repr??sentation binaire fractionn??e. Ce est souvent important pour les calculs financiers et d'autres .
Les fractions d??cimales
Une fraction d??cimale est une fraction o?? le d??nominateur est une puissance de dix.
Les fractions d??cimales sont g??n??ralement exprim??es sans d??nominateur, le s??parateur d??cimal ??tant ins??r??e dans le num??rateur (avec z??ros de t??te ajout??s si n??cessaire), ?? la position de la droite correspondant ?? la puissance dix du d??nominateur. par exemple, 8/10, 833/100, 83/1000, et 8/10000 sont exprim??s en:. 0 8, 8 33, 0 083 et 0 0008.... Dans les pays anglophones, un point (??) ou la p??riode est utilis?? comme s??parateur d??cimal (.); dans la plupart des autres langues une virgule est utilis??e.
La partie enti??re ou une partie int??grante d'un nombre d??cimal est la partie ?? gauche du s??parateur d??cimal (voir aussi fonction de-chauss??e). La partie du s??parateur d??cimal vers la droite est la partie fractionnaire; si consid??r?? comme un num??ro distinct, un z??ro est souvent ??crit en face. Surtout pour les nombres n??gatifs, nous devons faire la distinction entre la partie fractionnaire de la notation et la partie fractionnaire du nombre lui-m??me, parce que ce dernier obtient son propre signe moins. Il est habituel pour un nombre d??cimal qui est inf??rieure ?? une partie pour avoir un z??ro.
Z??ros apr??s la virgule ne sont pas n??cessaires, bien que dans la science, l'ing??nierie et les statistiques , ils peuvent ??tre conserv??s pour indiquer une pr??cision requise ou pour montrer un niveau de confiance dans l'exactitude du nombre:.. Alors que 0 080 et 0 08 sont num??riquement ??gal, dans l'ing??nierie 0. 080 sugg??re une mesure avec une erreur maximale de 1 partie en deux mille (?? 0. 0005), tandis que 0. 08 sugg??re une mesure avec une erreur maximale de 1 ?? deux cent (voir Chiffres significatifs).
D'autres nombres rationnels
Tout nombre rationnel qui ne peut ??tre exprim?? sous forme de fraction d??cimale a une infinie d??veloppement d??cimal unique, se terminant par d??cimales r??currentes.
Dix est le produit des premier et troisi??me nombres premiers , est plus grand que le carr?? de la deuxi??me nombre premier, et est un de moins que le cinqui??me nombre premier. Cela conduit ?? beaucoup de simples fractions d??cimales:
- 02/01 = 0,5
- 1/3 = 0,333333 ... (avec 3 r??p??ter)
- 1/4 = 0,25
- 05/01 = 0,2
- 1/6 = 0,166666 ... (avec 6 r??p??ter)
- 1/8 = 0,125
- 1/9 = 0,111111 ... (avec une r??p??tition)
- 10/01 = 0,1
- 11/01 = 0,090909 ... (avec r??p??tition 09)
- 1/12 = 0,083333 ... (avec 3 r??p??ter)
- 1/81 = ,012345679012 ... (avec 012.345.679 r??p??ter)
Autres facteurs premiers dans le d??nominateur donneront plus r??currents s??quences , voir par exemple 7, 13.
Qu'un nombre rationnel doit avoir un d??veloppement d??cimal fini ou p??riodique, peut ??tre consid??r??e comme une cons??quence de la division longue algorithme , en ce qu 'il n'y a que q-1 non nul possible restes de division par q, de sorte que le motif r??current auront une p??riode inf??rieure ?? q. Par exemple, pour trouver des 3/7 par une longue division:
0,4 2 8 5 7 1 4 ...
7) 3,0 0 0 0 0 0 0 0
2 8 30/7 = 4 r 2
2 0
1 4 20/7 = 2 r 6
6 0
5 6 8 60/7 = r 4
4 0
3 5 = 40/7 5 5 r
5 0
4 9 7 r = 50/7 1
1 0
7 7/10 1 = r 3
3 0
2 8 30/7 = 4 r 2 (nouveau)
2 0
etc
L'inverse de cette observation est que chaque r??currente d??cimale repr??sente un nombre rationnel p / q. Ceci est une cons??quence du fait la partie r??currente d'une repr??sentation d??cimale est, en fait, un infini s??rie g??om??trique qui r??sumer ?? un nombre rationnel. Par exemple,
Nombres r??els
Chaque nombre r??el a une (??ventuellement infini) repr??sentation d??cimale, ce est ?? dire, il peut ??tre ??crit comme
o??
- sign () est la fonction signe,
- a i ∈ {0,1, ..., 9} pour tout i ∈ Z, sont les chiffres d??cimaux, ??gal ?? z??ro pour tout i sup??rieur ?? un certain nombre (ce nombre ??tant le logarithme d??cimal de | x |).
Une telle somme converge i diminue, m??me se il ya une infinit?? de non nulle d'un i.
Nombres rationnels (par exemple p / q) avec facteurs premiers dans le d??nominateur autre que 2 et 5 (lorsque r??duit ?? termes les plus simples) ont un unique, repr??sentation d??cimale r??currente.
Consid??rez ces nombres rationnels qui ne ont que les facteurs 2 et 5 dans le d??nominateur, ce est ?? dire qui peut ??tre ??crit comme p / (2 ?? 5 b). Dans ce cas, il est une repr??sentation d??cimale de terminaison. Par exemple 1/1 = 1, 1/2 = 0,5, 3/5 = 0,6, 3/25 = 0,12 et 1306/1250 = 1,0448. Ces num??ros sont les seuls nombres r??els qui ne ont pas une repr??sentation d??cimale unique, comme ils peuvent aussi ??tre ??crites comme une repr??sentation qui a une r??currente 9, par exemple 1 = 0,99999 ..., 1/2 = 0,499999 ..., etc.
Cela laisse les nombres irrationnels . Ils ont ??galement unique repr??sentation d??cimale infinie, et peuvent ??tre caract??ris??s comme les num??ros dont les repr??sentations d??cimale ni fin, ni se reproduire.
Donc, en g??n??ral la repr??sentation d??cimale est unique, si l'on exclut les repr??sentations qui se terminent par un 9 r??currents.
Naturellement, le m??me trichotomie est valable pour une autre base-n syst??mes de num??ration de position:
- La repr??sentation de terminaison: o?? rationnelle le d??nominateur divise un certain n k
- Repr??sentation r??currente: autre rationnelle
- Non-terminaison, la repr??sentation non r??current: irrationnelle
et une version de cette vaut m??me pour les syst??mes de num??ration irrationnelle-base, tels que repr??sentation de base moyen d'or.
Histoire
Suit une liste chronologique des ??crivains d??cimales enregistr??es.
??crivains d??cimales
- . c 3500 - 2500 BC Elamites de l'Iran ??ventuellement utilis?? des formes pr??coces de syst??me d??cimal.
- . c 2900 BC ??gyptiens hi??roglyphes montrent compter en puissances de 10 (+ 1 million 400 000 ch??vres, etc.) - voir Ifrah, ci-dessous
- . c 2600 BC Civilisation de la vall??e de l'Indus , premi??re utilisation physique connu des d??cimales fractions dans le syst??me de poids ancienne: 1/20, 1/10, 1/5, 1/2. Voir poids et mesures ancienne vall??e de l'Indus
- . c 1400 BC chinoise ??crivains montrent familiarit?? avec le concept: par exemple, 547 est ??crit ??Cinq cents plus quatre d??cennies, plus de sept jours?? dans certains manuscrits
- . c 1200 BC Dans l'Inde ancienne , le Texte v??dique Yajurveda ??nonce les pouvoirs de 10, jusqu'?? 10 55
- c. 400 BC Pingala - d??veloppe le syst??me de nombre binaire pour le sanskrit prosodie, avec une cartographie claire au syst??me d??cimal en base 10
- c. 250 BC Archim??de r??dige le Sable Reckoner, qui prend d??cimal calcul jusqu'?? 10 80,000,000,000,000,000
- . c 100-200 Le Satkhandagama ??crit en Inde - premi??re utilisation des logarithmes d??cimaux
- c. 476-550 Aryabhata - utilise un syst??me de chiffrement alphab??tique pour les num??ros utilis??s z??ro
- c. 598-670 Brahmagupta - explique le Chiffres indo-arabes (syst??me num??rique moderne) qui utilise d??cimales des nombres entiers , entiers n??gatifs et z??ro
- . c 780-850 Muhammad ibn Musa al-Ḵwārizmī - premier ?? exposer sur algorism en dehors de l'Inde
- c. 920-980 Abu'l Hasan Ahmad ibn Ibrahim Al-Uqlidisi - premier traitement math??matique directe connue des fractions d??cimales.
- c. 1300-1500 Le Ecole Kerala en Inde du Sud - d??cimal nombres ?? virgule flottante
- 1548 / 49-1620 Simon Stevin - auteur de De thiende (la dixi??me)
- 1561-1613 Bartholemaeus Pitiscus - (??ventuellement) la notation d??cimale.
- 1550-1617 John Napier - utilisation de logarithme d??cimal comme un outil de calcul
- 1765 Johann Heinrich Lambert - discute (avec quelques si des preuves) mod??les dans expansions d??cimales de nombres rationnels et note une connexion avec le petit th??or??me de Fermat dans le cas de d??nominateurs premiers
- 1800 Karl Friedrich Gauss - utilise la th??orie des nombres pour expliquer syst??matiquement mod??les dans d??cimales expansions de nombres rationnels r??currents (par exemple, la relation entre la longueur de la p??riode de la partie r??currente et le d??nominateur, qui fractions avec le m??me d??nominateur ont r??currents parties d??cimales qui sont des changements de chaque d'autres, comme 1/7 et 2/7) et pose ??galement des questions qui restent ouvertes ?? ce jour (par exemple, un cas particulier de La conjecture de Artin sur les racines primitives: 10 est un g??n??rateur modulo p pour infinit?? de nombres premiers p)?.
- 1925 Louis Charles Karpinski - L'histoire de l'arithm??tique
- 1959 Werner Buchholz - Les doigts ou les mains? (Le Choix de repr??sentation d??cimale ou binaire)
- 1974 Hermann Schmid - Calcul d??cimal
- 2000 Georges Ifrah - L'histoire universelle des chiffres: De la Pr??histoire ?? l'invention de l'ordinateur
- 2003 Mike Cowlishaw - virgule d??cimale flottante: algorism pour les ordinateurs.
Les langues naturelles
Un syst??me d??cimal simple, dans lequel 11 est exprim??e en dix ?? une et 23 que de deux ?? dix-trois ans, se trouve dans les langues chinoises exception Wu, et Vietnamienne avec quelques irr??gularit??s. Japonais, Cor??en, et Thai ont import?? le syst??me d??cimal chinois. Beaucoup d'autres langues avec un syst??me d??cimal ont mots sp??ciaux pour les num??ros entre 10 et 20, et des d??cennies.
Langues incas telles que Quechua et Aymara ont un syst??me d??cimal presque simple, dans lequel 11 est exprim??e en dix avec un seul et 23 que de deux ?? dix avec trois.
Certains psychologues sugg??rent irr??gularit??s de chiffres dans une langue peut nuire ?? la capacit?? de comptage des enfants.