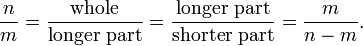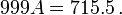Nombre irrationnel

En math??matiques , un nombre irrationnel est ne importe quel nombre r??el qui ne est pas un nombre rationnel - autrement dit, il se agit d'un nombre qui ne peut ??tre exprim??e comme une fraction m / n, o?? m et n sont des nombres entiers , avec n diff??rent de z??ro. Officieusement, cela signifie num??ros qui ne peuvent pas ??tre repr??sent??s comme des fractions simples. On peut en d??duire qu'ils ont ??galement ne peuvent pas ??tre repr??sent??s comme fin ou nombres d??cimaux, mais l'id??e est plus profond que cela. Bien qu'il puisse sembler ??trange au premier abord audience, presque tous les nombres r??els sont irrationnelles, dans un sens qui est d??fini plus pr??cis??ment ci-dessous. Peut-??tre que les num??ros les plus connus sont irrationnel π et √2.

Quand le rapport des longueurs des deux segments de ligne est irrationnel, les segments de ligne sont ??galement d??crits comme ??tant incommensurable, ce qui signifie qu'ils ne partagent aucune mesure en commun. Une mesure d'un segment de la ligne I est dans ce sens un segment de droite que J "mesures" I dans la mesure o?? un nombre de copies de l'ensemble J fix??es bout ?? bout occupent la m??me longueur que je.

Le num??ro est irrationnel.

Histoire

La premi??re preuve de l'existence de nombres irrationnels est g??n??ralement attribu??e ?? Hippasus de M??taponte, un Pythagore qui a probablement d??couvert tout en identifiant les c??t??s de la pentagramme. Cependant Pythagore croyait en l'absolu de num??ros, et ne pouvait pas accepter l'existence de nombres irrationnels. Il ne pouvait pas infirmer leur existence ?? travers la logique, mais ses convictions ne serait pas accepter l'existence de nombres irrationnels et donc, que la l??gende l'avait, il avait Hippasus noy??. Th??odore de Cyr??ne prouva l'irrationalit?? de la surds de nombres entiers jusqu'?? 17, mais se arr??taient l?? probablement parce que l'alg??bre qu'il a utilis?? ne pouvait pas ??tre appliqu??e ?? la racine carr??e de 17. Ce ne est que Eudoxe d??velopp?? une th??orie de rapports irrationnels qu'une base solide math??matique des nombres irrationnels a ??t?? cr????. ??l??ments d'Euclide livre 10 est d??di??e ?? la classification des grandeurs irrationnelles.

Le XVIe si??cle a vu l'acceptation de n??gatifs , int??grales et fractions num??ros. Le XVIIe si??cle a vu fractions d??cimales avec la notation moderne assez g??n??ralement utilis?? par les math??maticiens. Les cent prochaines ann??es ont vu les nombres imaginaires deviennent un outil puissant dans les mains de Abraham de Moivre, et surtout de Leonhard Euler . L'ach??vement de la th??orie des nombres complexes dans le XIXe si??cle a entra??n?? la diff??renciation des irrationnels en nombres alg??briques et transcendantes, la preuve de l'existence de nombres transcendants, et la r??surgence de l'??tude scientifique de la th??orie des irrationnels, largement ignor??s depuis Euclide . L'ann??e 1872 a vu la publication des th??ories de Karl Weierstrass (par son ??l??ve Kossak), Heine ( Crelle, 74), Georg Cantor (Annalen, 5), et Richard Dedekind. M??ray avait pris en 1869 le m??me point de d??part que Heine, mais la th??orie est g??n??ralement appel?? ?? l'ann??e 1872. La m??thode de Weierstrass a ??t?? compl??tement ??nonc??e par Salvatore Pincherle en 1880, et a re??u de Dedekind importance suppl??mentaire par le travail de l'auteur plus tard (1888) et l'approbation r??cente par Paul Tannery (1894). Weierstrass, Cantor et Heine fondent leurs th??ories sur la s??rie infinie, alors que Dedekind fonde son sur l'id??e d'un couper (Schnitt) dans le syst??me des nombres r??els , en s??parant tous les nombres rationnels en deux groupes ayant certaines propri??t??s caract??ristiques. Le sujet a re??u des contributions ult??rieures aux mains de Weierstrass, Kronecker (Crelle, 101), et M??ray.

Fractions continues, ??troitement li??s ?? des nombres irrationnels (et en raison de Cataldi, 1613), ont re??u une attention aux mains de Euler , et ?? l'ouverture de la dix-neuvi??me si??cle ont ??t?? mis en ??vidence ?? travers les ??crits de Lagrange . Dirichlet ??galement ajout?? ?? la th??orie g??n??rale, de m??me que de nombreux contributeurs aux applications de l'objet.

Lambert se est av??r?? (1761) que π ne peut pas ??tre rationnelle, et que e ⁿ est irrationnel si n est rationnel (sauf n = 0). Bien que la preuve de Lambert est souvent dite incompl??te, ??valuations modernes prennent en charge comme satisfaisante, et en fait pour son temps inhabituellement rigoureux. Legendre (1794), apr??s l'introduction du Fonction de Bessel-Clifford, fourni une preuve pour montrer que π ² est irrationnel, o?? il suit imm??diatement que π est irrationnel aussi. L'existence de nombres transcendants premier a ??t?? cr???? par Liouville (1844, 1851). Plus tard, Georg Cantor (1873) a prouv?? leur existence par une m??thode diff??rente, qui a montr?? que chaque intervalle dans les reals contient des nombres transcendants. Charles Hermite (1873) d'abord prouv?? transcendantale, et Ferdinand von Lindemann (1882), ?? partir des conclusions de Hermite, a montr?? le m??me pour π. La preuve de Lindemann a ??t?? beaucoup simplifi??e par Weierstrass (1885), encore par David Hilbert (1893), et a finalement ??t?? rendu ??l??mentaire par Adolf Hurwitz et Paul Albert Gordan.

Exemple preuves

La racine carr??e de 2

L'irrationalit?? de la racine carr??e de 2 peut ??tre prouv??e en supposant qu'il est rationnel et d'en d??duire une contradiction, un argument appel?? par reductio ad absurdum. L'argument suivant fait appel ?? deux reprises sur le fait que le carr?? d'un nombre impair est toujours impair.

Si √ 2 est rationnel, il a la forme m / n pour des entiers m, n, m??me pas les deux. Puis m ?? = 2 n ?? o?? m est encore, dit m = 2 p. Ainsi 4 p ?? = 2 n ?? donc 2 p ?? = n ?? o?? n est ??galement m??me, une contradiction.

Une autre preuve

Ce qui suit reductio argument ad absurdum est moins bien connu. Il utilise les informations suppl??mentaires √2> 1.

1. Supposons que √2 est un nombre rationnel. Cela signifie qu'il existe des entiers m et n avec n ≠ 0 tel que m / n = √2.
2. Puis √2 peut ??galement ??tre ??crit comme une fraction irr??ductible m / n avec des nombres entiers positifs, parce √2> 0.
3. Puis , Parce .
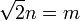4. Depuis √2> 1, il se ensuit que m> n, qui ?? son tour implique que m> 2 n - m.
5. Ainsi, la fraction m / n pour √2, qui selon le point (2) est d??j?? en termes plus bas, est repr??sent?? par (3) en termes strictement inf??rieurs. Ce est une contradiction, donc l'hypoth??se que √2 est rationnel doit ??tre fausse.

De m??me, assumer un triangle isoc??le dont la jambe droite et hypot??nuse avoir des longueurs n et m entiers respectifs. Par le th??or??me de Pythagore , le rapport m / n est ??gal ?? √2. Il est possible de construire par un classique r??gle et au compas construction un triangle rectangle isoc??le petits dont la jambe et l'hypot??nuse ont des longueurs respectives m - n et 2 n - m. Que la construction se av??re l'irrationalit?? de √2 par le genre de m??thode qui a ??t?? employ??e par les anciens g??om??tres grecs.

La racine carr??e de 10 et au-del??

Si √ 10 est rationnel, dire m / n, m ² = 10 n ^2. Cependant, en notation d??cimale, chaque carr?? se termine par un nombre pair de z??ros. Alors m ² et 10 n ² en d??cimal doit se terminer par respectivement un nombre pair et impair de z??ros, une contradiction.

Plus g??n??ralement, dans ne importe quel r radix qui ne est pas lui-m??me un carr??, chaque carr?? se termine par un m??me nombre de z??ros, o?? √ 10 _r en base r est irrationnel, ce est-?? √ r est irrationnel. Il se ensuit que les seuls entiers avec racines carr??es rationnelles sont des carr??s. Comme un cas au point, 2 ne est pas un carr??, et 2 en binaire est 10 _2. (Notez la convention de subscripting chiffres non d??cimal avec leur base, pour ??viter toute ambigu??t??. Dans le cadre de cette convention, les indices sont compris comme en d??cimal, ne ??tant pas eux-m??mes en indice.)

Pour aller plus loin, nous pouvons consid??rer m ^k = r ?? n ^k pour tout entiers r et k. Si r ≠ u ^k pour tout entier u, alors R a au moins un facteur premier p ??lev??e ?? un exposant qui ne est pas divisible par k. Comme tous les exposants dans le Premier factorisation de m ^k sont divisibles par k, pour l'??quation de tenir, la factorisation de n ^k doit contenir p ??lev?? ?? une puissance qui ne est pas non divisible par k. Mais ce est clairement impossible. Ainsi, pour tout entiers r et ^k, k √ r est irrationnel si r ≠ u ^k pour tout entier u. Ce r??sultat d??coule ??galement du fait que soulever un nombre rationnel non entier d'une puissance enti??re ne peut jamais ??galer un nombre entier plus une.

Le nombre d'or

Quand un segment de droite est divis?? en deux sous-segments disjoints de telle sorte que le rapport de l'ensemble de la partie la plus longue est ??gal au rapport de la partie la plus longue de la partie la plus courte, alors que le ratio est le nombre d'or , ??gal ??

Supposons que ce est un nombre rationnel n / m en termes plus bas. N Prendre comme la longueur de l'ensemble et m la longueur de la partie plus longue. Ensuite, n> m, et la longueur de la partie plus courte est le N - m. Ensuite, nous avons

Toutefois, cela met une fraction d??j?? en termes plus bas dans la contradiction de termes inf??rieurs. Par cons??quent, l'hypoth??se initiale, que le nombre d'or est rationnel, est fausse.

Logarithmes

Peut-??tre les num??ros les plus faciles ?? prouver pour ??tre irrationnelle sont certains logarithmes . Voici une preuve par reductio ad absurdum qui se connectent ₂ 3 est irrationnelle:

• Pr??sumer que log ₂ 3 est rationnel. Pour certains entiers positifs m et n, nous avons log ₂ = 3 m / n.
• Il en r??sulte que 2 ^{m / n} = 3.
• Soulevez chaque c??t?? ?? l'n puissance, trouvez 2 ^m = 3 ^n.
• Mais 2 ?? une puissance enti??re sup??rieure ?? 0 est pair (car au moins l'un de ses facteurs premiers est ??gal ?? 2) et 3 ?? une puissance enti??re plus grande que 0 est impair (parce qu'aucun de ses facteurs premiers est ??gal ?? 2), de sorte que l'hypoth??se de d??part est fausse.

Des cas comme log ₁₀ 2 peuvent ??tre trait??s de mani??re similaire.

Irrationnels et alg??briques transcendantales

Presque tous les nombres irrationnels sont transcendantale et tout nombres transcendants sont irrationnelles: l'article sur nombres transcendants ??num??re plusieurs exemples e ^r et π ^r sont irrationnelles si r ≠ 0 est rationnel; e ^π est aussi irrationnel..

Une autre fa??on de construire des nombres irrationnels est aussi irrationnel nombres alg??briques, ce est ?? dire sous forme de z??ros de polyn??mes ?? coefficients entiers: commencent par une ??quation polynomiale

p (x) = a _n x ⁿ + a _n-1 x ^n-1 + ... + a ₁ x + a ₀ = 0

o?? les coefficients a _i sont des nombres entiers. Supposons que vous savez qu'il existe un nombre r??el x avec p (x) = 0 (par exemple si n est impair et un _n est non nul, en raison de la th??or??me de la valeur interm??diaire). Les seules racines rationnelles possibles de cette ??quation polynomiale sont de la forme R / s o?? R est un diviseur de ₀ et s est un diviseur de _n; il ya seulement un nombre fini de ces candidats que vous pouvez tout ch??que ?? la main. Si aucun d'eux ne est une racine de p, alors x doit ??tre irrationnel. Par exemple, cette technique peut ??tre utilis??e pour montrer que x = (2 ^1/2 + 1) ^1/3 est irrationnel: nous avons (x ^{3-1) 2} = 2 et donc x ^6-2 x ^3-1 = 0 et ce dernier polyn??me n'a pas de racines rationnelles (les seuls candidats pour v??rifier sont ?? 1).

Du fait que les nombres alg??briques forment un domaine, de nombreuses nombres irrationnels peut ??tre construit en combinant des nombres transcendants et alg??briques. Par exemple 3π + 2, + π √ √ 2 et e 3 sont irrationnelles (et m??me transcendantale).

Expansions d??cimales

L'expansion d??cimale d'un nombre irrationnel ne se r??p??te jamais ou se termine, contrairement ?? un nombre rationnel.

Pour le montrer, supposons que nous diviser des nombres entiers n par m (o?? m est non nul). Quand division longue est appliqu??e ?? la division du n par m, m seulement restes sont possibles. Si 0 appara??t comme un reste, le d??veloppement d??cimal se termine. Si 0 ne se produit jamais, alors l'algorithme peut fonctionner au plus m - 1 ??tapes sans utiliser reste plus d'une fois. Apr??s cela, un reste doit se reproduire, puis les r??p??titions d'expansion d??cimales!

Inversement, supposons que nous sommes confront??s ?? un r??currente d??cimal, nous pouvons prouver que ce est une fraction de deux nombres entiers. Par exemple:

Ici la longueur de la repitend est 3. On multiplie par ³ 10:

Notez que, depuis, nous avons multipli?? par 10 ?? la puissance de la longueur de la partie ?? r??p??ter, nous avons r??orient?? les chiffres ?? gauche de la virgule exactement que de nombreux postes. Par cons??quent, l'extr??mit?? de queue de 1000 A correspond ?? l'extr??mit?? de queue de A exactement. Ici, ?? la fois A et 1000 A 162 ont r??p??ter ?? la fin.

Par cons??quent, lorsque l'on soustrait une des deux parties, l'extr??mit?? de queue de 1000 A annule hors de l'extr??mit?? de queue de A:

Puis

qui est un quotient d'entiers et donc un nombre rationnel.

Questions ouvertes

On ne sait pas si π + π ou e - e est irrationnel ou non. En fait, il n'y a pas de paire de nombres entiers non nuls m et n pour laquelle il est connu que m + π ne est irrationnel ou non. En outre, on ne sait pas si l'ensemble {π, e} est alg??briquement ind??pendants sur Q.

On ne sait pas si les deux ^e, π ^e, π ^√2, Constante de Catalan, ou Euler-Mascheroni Gamma γ constants sont irrationnelles.

L'ensemble des irrationnels

Depuis les r??els forment un ensemble non d??nombrable dont les rationnels sont un sous-ensemble d??nombrable, l'ensemble compl??mentaire de irrationnels est incalculable.

Sous l'habitude ( Euclidienne) fonction de distance d (x, y) = | x - y |, les chiffres r??els sont un espace m??trique et donc aussi un espace topologique. Restriction de la fonction de distance euclidienne donne les irrationnels la structure d'un espace m??trique. ??tant donn?? que le sous-espace de irrationnels ne est pas ferm??, la m??trique induite ne est pas complet. Cependant, ??tant un G-delta ensemble - ce est ?? dire, une intersection d??nombrable de parties ouvertes - dans un espace m??trique complet, l'espace des irrationnels est topologiquement compl??te: ce est, il est une m??trique sur les irrationnels induisant la m??me topologie que la restriction de la m??trique euclidienne, mais ?? l'??gard desquels les irrationnels sont complets. On peut voir cela sans savoir le fait mentionn?? ci-dessus sur les jeux de G-delta: le d??veloppement en fraction continue d'un nombre irrationnel d??finit un hom??omorphisme de l'espace des irrationnels ?? l'espace de toutes les s??quences de nombres entiers positifs, qui est facilement visibles pour ??tre compl??tement m??trisable.

En outre, l'ensemble de tous irrationnels est un espace m??trique d??connect??.