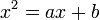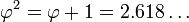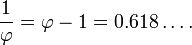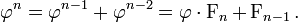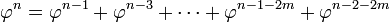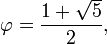Nombre d'or
Renseignements g??n??raux
Enfants SOS ont produit une s??lection d'articles de wikipedia pour les ??coles depuis 2005. parrainage d'enfants aide les enfants un par un http://www.sponsor-a-child.org.uk/ .


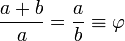 .
. Dans les math??matiques et les arts , deux quantit??s sont dans le rapport d'or si le rapport de la somme des quantit??s de la plus grande quantit?? est ??gale au rapport de la quantit?? plus grande de la plus petite. La figure de droite illustre la relation g??om??trique. Exprim??e alg??briquement:
o?? la lettre grecque phi (  ) Repr??sente le nombre d'or. Sa valeur est:
) Repr??sente le nombre d'or. Sa valeur est:
Le nombre d'or est aussi appel?? la section d'or (en latin: aurea sectio) ou d'or. Autres noms incluent extr??me et rapport moyen, section m??diane, la divine proportion, section divine (latin: sectio divina), la proportion d'or, coupe d'or, et nombre d'or.
Beaucoup 20??me si??cle artistes et architectes ont proportionn?? leurs travaux pour rapprocher le rapport-particulier d'or sous forme de rectangle d'or, dans lequel le rapport de la c??t?? le plus long au plus court est le rapport-croyant cette proportion en or pour ??tre esth??tiquement agr??able (voir Applications et observations ci-dessous). math??maticiens depuis Euclide ont ??tudi?? les propri??t??s du nombre d'or, y compris son apparition dans les dimensions d'une pentagone r??gulier et dans un rectangle d'or, qui peut ??tre coup?? en un carr?? et un petit rectangle avec le m??me rapport d'aspect. Le nombre d'or a ??galement ??t?? utilis?? pour analyser les proportions des objets naturels ainsi que des syst??mes artificiels tels que march??s financiers, dans certains cas, sur la base des crises douteuses aux donn??es.
Calcul
| |
| Binaire | 1,1001111000110111011 ... |
| D??cimal | 1,6180339887498948482 ... |
| Hexad??cimal | 1.9E3779B97F4A7C15F39 ... |
| Fraction continue |  |
| Forme alg??brique |  |
| S??rie infinie | 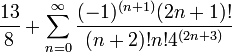 |
Deux grandeurs a et b sont dits ??tre dans le rapport d'or φ si:
Un proc??d?? pour trouver la valeur de φ est de commencer avec la fraction gauche. Gr??ce ?? la simplification de la fraction et son remplacement en b / a = 1 / φ,
il est d??montr?? que
Multipliant par φ donne
qui peuvent ??tre reconstitu??es ??
En utilisant la formule quadratique , deux solutions sont obtenues:
et
En raison du fait que φ est le rapport entre la longueur et la largeur d'un rectangle, qui sont non nuls, la solution doit ??tre choisie positif:
Histoire


Le nombre d'or a fascin?? les intellectuels occidentaux de divers int??r??ts pendant au moins 2400 ann??es. Selon Mario Livio:
Certains des plus grands esprits math??matiques de tous ??ges, de Pythagore et Euclide dans la Gr??ce antique , par le math??maticien italien m??di??vale Leonardo de Pise et de l'astronome de la Renaissance Johannes Kepler , ?? aujourd'hui personnalit??s scientifiques comme Oxford physicien Roger Penrose, ont pass?? des heures interminables sur ce rapport simple et ses propri??t??s. Mais la fascination avec le nombre d'or ne se limite pas simplement ?? des math??maticiens. Biologistes, artistes, musiciens, historiens, architectes, psychologues, et m??me mystiques ont r??fl??chi et d??battu la base de son ubiquit?? et d'appel. En fait, il est probablement juste de dire que le ratio d'or a inspir?? des penseurs de toutes les disciplines comme aucun autre nombre dans l'histoire des math??matiques.
Gr??ce antique math??maticiens abord ??tudi?? ce que nous appelons maintenant le nombre d'or en raison de son apparition fr??quente dans la g??om??trie . La division d'une ligne dans (la section d'or) "rapport extr??me et moyenne" est important dans la g??om??trie de la r??guli??re pentagrammes et pentagones. La Grecs g??n??ralement attribu??e la d??couverte de ce concept ?? Pythagore ou de son adeptes. Le pentagramme r??guli??re, qui a un pentagone r??gulier inscrit en son sein, ??tait le symbole des pythagoriciens.
Euclid s ' Elements ( grec : Στοιχεῖα) fournit la d??finition ??crite d'abord connu de ce qu'on appelle maintenant le nombre d'or: "Une ligne droite est dit avoir ??t?? coup?? dans l'extr??me et le ratio signifie lorsque, comme l'ensemble de la ligne est de la plus grande secteur , est ainsi le plus ?? moins. " Euclid explique une construction pour la coupe (coupe) une ligne "en rapport extr??me et moyenne", ce est ?? dire, le nombre d'or. Tout au long des ??l??ments, plusieurs propositions ( th??or??mes dans la terminologie moderne) et leurs preuves emploient le nombre d'or. Certaines de ces propositions montrent que le nombre d'or est un nombre irrationnel .
Le nom de ??rapport extr??me et moyenne" ??tait le terme principal utilis?? ?? partir du 3??me si??cle avant notre ??re jusqu'?? environ le 18??me si??cle.
L'histoire moderne de la proportion dor??e commence par Luca Pacioli De divina proportione de 1509, qui a captur?? l'imagination des artistes, des architectes, des scientifiques et mystiques avec les propri??t??s, math??matiques et autres, de la proportion dor??e.
La premi??re approximation connue du (inverse) de nombre d'or par une fraction d??cimale , a d??clar?? que "environ 0,6180340", a ??t?? ??crit en 1597 par Michael Maestlin du Universit?? de T??bingen dans une lettre ?? son ancien ??l??ve Johannes Kepler .
Depuis le 20??me si??cle , le nombre d'or a ??t?? repr??sent??e par le lettre grecque ou Φ φ ( phi, apr??s Phidias, sculpteur qui est dit avoir employ?? il) ou, moins fr??quemment par τ ( tau, la premi??re lettre du grec ancien coupe-τομή signifie racine).
Chronologie
Chronologie selon Priya Hemenway:
- Phidias (490-430 BC) a fait les Parth??non statues qui semblent incarner le nombre d'or.
- Platon (427-347 avant JC), dans son Tim??e, d??crit cinq solides r??guliers possibles (les des solides platoniciens : le t??tra??dre , cube , l'octa??dre , dod??ca??dre, et icosa??dre), dont certaines sont en relation avec le nombre d'or.
- Euclid (.. c 325 c 265 BC), dans ses ??l??ments , a donn?? la premi??re d??finition enregistr??e du nombre d'or, qu'il a appel??, que traduit en anglais, ??extr??me et le ratio signifie" (en grec: ἄκρος καὶ μέσος λόγος).
- Fibonacci (1170-1250) a mentionn?? la s??rie num??rique porte aujourd'hui son nom dans son Liber Abaci; le rapport des ??l??ments s??quentiels de la suite de Fibonacci se approche asymptotiquement le rapport d'or.
- Luca Pacioli (1445-1517) d??finit le nombre d'or comme le ??divine proportion?? dans son Divina Proportione.
- Michael Maestlin (1550-1631) publie le rapprochement d'abord connu du (inverse) nombre d'or comme une fraction d??cimale .
- Johannes Kepler (1571-1630) prouve que le nombre d'or est la limite du ratio des nombres de Fibonacci cons??cutifs, et d??crit le nombre d'or comme un ??joyau??: ??g??om??trie a deux grands tr??sors: l'un est le th??or??me de Pythagore , et l'autre la division d'une ligne en rapport extr??me et moyenne; la premi??re on peut comparer ?? une mesure de l'or, la deuxi??me nous pouvons nommer un bijou pr??cieux ". Ces deux richesses sont combin??s dans le Kepler triangle.
- Charles Bonnet (1720-1793) souligne que dans la spirale phyllotaxie des plantes aller dans le sens horaire et anti-horaire ??taient souvent deux s??ries de Fibonacci successifs.
- Martin Ohm (1792-1872) est consid??r?? comme le premier ?? utiliser le terme goldener Schnitt (section or) pour d??crire ce rapport, en 1835.
- ??douard Lucas (1842-1891) donne la s??quence num??rique maintenant connu comme la s??quence de Fibonacci de son nom actuel.
- Mark Barr (20e si??cle) sugg??re la lettre phi grec (φ), la premi??re lettre du nom de sculpteur grec Phidias, comme un symbole pour le nombre d'or.
- Roger Penrose (b.1931) a d??couvert un motif sym??trique qui utilise le nombre d'or dans le domaine de pavages ap??riodiques, qui ont conduit ?? de nouvelles d??couvertes sur quasicristaux.
Applications et observations
Esth??tique
De Divina Proportione, un ouvrage en trois volumes par Luca Pacioli, a ??t?? publi?? en 1509. Pacioli, un Franciscain fr??re, a ??t?? surtout connu en tant que math??maticien, mais il a ??galement ??t?? form?? et vivement int??ress?? par l'art. De Divina Proportione explor?? les math??matiques de la proportion dor??e. Bien qu'il est souvent dit que Pacioli a pr??conis?? l'application de la proportion dor??e pour obtenir, des proportions harmonieuses agr??ables, Livio souligne que l'interpr??tation a ??t?? attribu??e ?? une erreur en 1799, et que Pacioli effectivement pr??conis?? la Syst??me de Vitruve de proportions rationnelles. Pacioli a ??galement vu signification religieuse catholique dans le rapport, qui a conduit ?? le titre de son travail. Contenant des illustrations de solides r??guliers par Leonardo da Vinci , de longue date, l'ami et collaborateur de Pacioli, De Divina Proportione ??tait une grande influence sur des g??n??rations d'artistes et d'architectes de m??me.
Architecture

La fa??ade de l'Parth??non ainsi que des ??l??ments de sa fa??ade et ailleurs sont dit par certains d'??tre circonscrites par des rectangles d'or. D'autres chercheurs nier que les Grecs avaient toute association esth??tique avec nombre d'or. Par exemple, Midhat J. Gazal?? dit, "Ce ne est que Euclide, cependant, que les propri??t??s math??matiques du nombre d'or ont ??t?? ??tudi??s. Dans les ??l??ments (308 BC), le math??maticien grec simplement consid??r?? ce nombre comme un nombre irrationnel int??ressant, dans le cadre de les ratios moyens et extr??mes. Sa pr??sence dans pentagones r??guliers et d??cagones a ??t?? d??ment observ??es, ainsi que dans le dod??ca??dre (une poly??dre r??gulier dont les faces sont douze pentagones r??guliers). Il est en effet exemplaire que la grande Euclid, contrairement aux g??n??rations de mystiques qui ont suivi, traiterait sobrement ce nombre pour ce qu'elle est, sans y attacher autre que ses propri??t??s de fait. "Et Keith Devlin dit: ??Certes, l'affirmation souvent r??p??t??e que le Parth??non ?? Ath??nes est bas??e sur le nombre d'or ne est pas soutenu par des mesures r??elles. En fait, toute l'histoire sur les Grecs et nombre d'or semble ??tre sans fondement. La seule chose nous savons pour s??r est que Euclide, dans son c??l??bre ouvrage Elements, ??crit vers 300 avant JC, a montr?? comment calculer sa valeur ". Pr??s de sources contemporaines comme Vitruve discuter exclusivement des proportions qui peuvent ??tre exprim??s en nombres entiers, ce est ?? dire en rapport, par opposition ?? des proportions irrationnelles.
A 2004 analyse g??om??trique des recherches ant??rieures dans le Grande Mosqu??e de Kairouan r??v??le une application coh??rente du nombre d'or dans toute la conception, selon Boussora et Mazouz. Ils ont trouv?? ratios fermer le nombre d'or dans la proportion globale du plan et dans le dimensionnement de l'espace de pri??re, le tribunal et le minaret. Les auteurs notent toutefois que les zones o?? les taux proches du nombre d'or ont ??t?? trouv??s ne font pas partie de la construction d'origine, et th??orisent que ces ??l??ments ont ??t?? ajout??s dans une reconstruction.
Les Suisses architecte Le Corbusier, c??l??bre pour ses contributions ?? la moderne style international, centr?? sa philosophie de conception sur les syst??mes de l'harmonie et de proportion. La foi de Le Corbusier ?? l'ordre math??matique de l'univers a ??t?? ??troitement li?? ?? la proportion dor??e et la s??rie de Fibonacci, qu'il a d??crit comme "rythmes apparents ?? l'??il et clairs dans leurs relations avec l'autre. Et ces rythmes sont ?? la racine m??me de les activit??s humaines. Ils r??sonnent chez l'homme par une fatalit?? biologique, m??me in??vitable amende qui provoque le trac?? sur la section d'or par des enfants, des vieillards, des sauvages et les savants. "
Le Corbusier a explicitement utilis?? le nombre d'or dans son Syst??me pour le Modulor ??chelle de proportion architectural. Il a vu ce syst??me comme une continuation de la longue tradition de Vitruve, de L??onard de Vinci " Homme de Vitruve ", le travail de Leon Battista Alberti, et d'autres qui ont utilis?? les proportions du corps humain pour am??liorer l'apparence et la fonction de l'architecture . En plus du nombre d'or, Le Corbusier bas??e sur le syst??me mesures humaines, les nombres de Fibonacci , et la double unit??. Il a pris suggestion du nombre d'or dans des proportions humaines ?? l'extr??me: il sectionn?? la hauteur de son mod??le corps humain au niveau du nombril avec les deux sections de nombre d'or, puis subdivis?? ces sections dans nombre d'or au niveau des genoux et de la gorge; il a utilis?? ces proportions de nombre d'or dans le Syst??me Modulor. 1927 Villa Stein de Le Corbusier ?? Garches illustr?? la demande du syst??me Modulor. Rectangulaire sol le plan de la villa, l'altitude et la structure interne des rectangles d'or pr??s approximatives.
Un autre architecte suisse, Mario Botta, fonde beaucoup de ses dessins sur des figures g??om??triques. Plusieurs maisons priv??es, il a con??u en Suisse sont compos??es de carr??s et des cercles, des cubes et des cylindres. Dans une maison, il a con??u en Origlio, le nombre d'or est la proportion entre la section centrale et les sections lat??rales de la maison.
Dans un livre r??cent, auteur Jason Elliot sp??cul?? que le nombre d'or a ??t?? utilis?? par les concepteurs de la Naqsh-e Jahan Square et la mosqu??e de Lotfollah adjacente.
Peinture

Le philosophe du 16??me si??cle Heinrich Agrippa a attir?? un homme sur un pentagramme int??rieur d'un cercle, ce qui implique une relation avec le nombre d'or.
Leonardo da Vinci illustrations s 'de poly??dres dans De divina proportione (Sur la Divine Proportion) et son point de vue que certaines proportions corporelles pr??sentent le nombre d'or ont conduit certains chercheurs ?? sp??culer que il a incorpor?? le nombre d'or dans ses peintures. Mais la suggestion que sa Mona Lisa , par exemple, emploie des proportions de nombre d'or, ne est pas pris en charge par quoi que ce soit dans les propres ??crits de L??onard de Vinci. De m??me, bien que le Homme de Vitruve est souvent montr?? en relation avec le nombre d'or, les proportions de la figure ne correspond pas r??ellement, et le texte ne mentionne que les rapports de nombres entiers.
Salvador Dal??, influenc?? par les oeuvres de Matila Ghyka, utilis?? explicitement le nombre d'or dans son chef-d'??uvre, La Derni??re C??ne. Les dimensions de la toile sont un rectangle d'or. Un grand dod??ca??dre, en perspective de sorte que les bords sont en nombre d'or ?? une autre, est suspendu au-dessus et derri??re J??sus et domine la composition.
Mondrian a ??t?? dit d'avoir utilis?? la section d'or abondamment dans ses peintures g??om??triques, bien que d'autres experts (y compris critique Yve-Alain Bois) ont contest?? cette all??gation.
Une ??tude statistique sur 565 ??uvres d'art de diff??rents grands peintres, effectu??es en 1999, a constat?? que ces artistes ne avaient pas utilis?? le nombre d'or de la taille de leurs toiles. L'??tude a conclu que le ratio moyen des deux c??t??s des tableaux ??tudi??s est de 1,34, avec des moyennes pour les artistes individuels allant de 1,04 (Goya) ?? 1,46 (Bellini). D'autre part, Pablo Tosto r??pertori?? plus de 350 ??uvres d'artistes bien connus, dont plus de 100 qui ont toiles avec rectangle d'or et de racines-cinq proportions, et d'autres avec des proportions comme root-2, 3, 4 et 6.
la conception du livre

Selon Jan Tschichold,
Il fut un temps o?? les ??carts de la page vraiment belles proportions 2: 3, 1: √3, et la section d'or ??taient rares. Beaucoup de livres produites entre 1550 et 1770 montrent que ces proportions exactement, ?? l'int??rieur d'un demi-millim??tre.
Design industriel
Certaines sources affirment que le nombre d'or est couramment utilis?? dans la conception de tous les jours, par exemple dans les formes de cartes postales, cartes ?? jouer, des affiches, des t??l??viseurs ?? ??cran large, les photographies et les plaques d'interrupteur de lumi??re.
Musique
Ernő Lendva?? analyse Les ??uvres de B??la Bart??k comme ??tant fond??e sur deux syst??mes oppos??s, celui du nombre d'or et les ??chelle acoustique, bien que d'autres savants de musique rejettent cette analyse. Dans Bartok Musique pour cordes, percussion et c??lesta la progression de xylophone se produit ?? des intervalles 1: 2: 3: 5: 8: 5: 3: 2: 1. Compositeur fran??ais Erik Satie a utilis?? le nombre d'or dans plusieurs de ses pi??ces, y compris Sonneries de la Rose + Croix. Le nombre d'or est ??galement apparente dans l'organisation des sections dans la musique de Debussy Reflets dans l'eau (reflets dans l'eau), des images (1??re s??rie, 1905), dans lequel "la s??quence de touches est marqu??e par les intervalles 34, 21, 13 et 8, et l'apog??e principal se trouve ?? la position phi ??.
Le musicologue Roy Howat a observ?? que les limites formelles de La Mer correspondent exactement ?? la section d'or. Trezise trouve la preuve intrins??que "remarquable", mais avertit le lecteur que aucune preuve ??crite ou rapport?? sugg??re que Debussy a cherch?? consciemment de telles proportions.
Pearl Batteries positionne les bouches d'a??ration sur ses mod??les Master prime bas??e sur le nombre d'or. La soci??t?? affirme que cette disposition am??liore la r??ponse des graves et a demand?? une brevet sur cette innovation.
Bien que Heinz Bohlen a propos?? la non-Octave-de r??p??ter ??chelle 833 cents sur la base tons combin??s, les relations avec les caract??ristiques de r??glage bas?? sur le nombre d'or. Comme un intervalle musical le rapport 1,618 833,090 ... est ... cents (Play).
Nature

Adolf Zeising, dont le principal int??r??t ??taient les math??matiques et la philosophie, trouve le nombre d'or exprim?? dans la disposition des branches le long des tiges des plantes et des veines dans les feuilles. Il a ??tendu ses recherches aux squelettes d'animaux et les ramifications de leurs veines et des nerfs, les proportions de compos??s chimiques et la g??om??trie de cristaux, m??me ?? l'utilisation de proportion dans les efforts artistiques. Dans ces ph??nom??nes il a vu le nombre d'or fonctionnant comme une loi universelle. Dans le cadre de son plan pour les proportions du corps humain ?? base de dor?? rapport, Zeising a ??crit en 1854 d'une loi universelle ??dans lequel est contenue rez-de-principe de toute formative se effor??ant pour la beaut?? et l'exhaustivit?? dans les domaines de la nature et de l'art, et qui impr??gne, comme un id??al capitale spirituelle, toutes les structures, formes et proportions, que ce soit cosmique ou individuel, organique ou inorganique, acoustique ou optique; "qui trouve sa pleine r??alisation, cependant, dans la forme humaine.
En 2010, la revue Science a rapport?? que le nombre d'or est pr??sent ?? l'??chelle atomique dans la r??sonance magn??tique des spins dans les cristaux de niobate de cobalt.
Plusieurs chercheurs ont propos?? des liens entre le nombre d'or et g??nome humain ADN .
Cependant, certains ont fait valoir que la plupart des manifestations apparentes de l'or signifie dans la nature, en particulier en ce qui concerne les dimensions des animaux, sont en fait fictive.
Optimisation
Le nombre d'or est la cl?? du M??thode du nombre d'or.
??tudes sur la perception
Des ??tudes men??es par des psychologues, en commen??ant par Fechner, ont ??t?? con??ues pour tester l'id??e que le nombre d'or joue un r??le dans la perception humaine de beaut??. Alors que Fechner trouv?? une pr??f??rence pour des rapports de rectangle centr?? sur le nombre d'or, les tentatives ult??rieures de tester soigneusement une telle hypoth??se ont ??t??, au mieux, peu concluantes.
Math??matiques
Nombre d'or conjugu??
La racine n??gative de l'??quation quadratique pour φ (la ??racine conjugu??") est
La valeur absolue de cette quantit?? (≈ 0,618) correspond au rapport de la longueur prise dans l'ordre inverse (plus courte longueur de segment sur la longueur du plus long segment, b / a), et est parfois d??sign?? comme ??tant le rapport conjugu?? d'or. Elle est not??e ici par la capitale Phi (Φ):
Alternativement, Φ peut ??tre exprim??e comme
Ceci illustre la propri??t?? unique du nombre d'or parmi des nombres positifs, qui
ou son inverse:
Cela signifie 0,61803 ...: 1 = 1: 1,61803 ....
Courts preuves de l'irrationalit??
Contradiction d'une expression en termes plus bas

Rappelons que:
- l'ensemble est la partie la plus plus la partie la plus courte;
- l'ensemble est ?? la partie plus que la partie ne est plus ?? la partie plus courte.
Si nous appelons l'ensemble n et le plus partie m, puis la seconde d??claration ci-dessus devient
- n est ??gal ?? m comme m est n - m,
ou alg??briquement
Pour dire que φ est des moyens rationnels que φ est une fraction n / m o?? n et m sont des nombres entiers. Nous pouvons prendre la N / m pour ??tre en termes les plus bas et n et m soit positif. Mais si n / m est en termes plus bas, alors l'identit?? ??tiquet?? (*) ci-dessus dit m / (n - m) est en termes encore plus bas. Ce est une contradiction qui d??coule de l'hypoth??se que φ est rationnel.
D??rivation de l'irrationalit?? des √5
Une autre preuve, peut-??tre ?? court plus commun??ment connu-de l'irrationalit?? de la proportion dor??e fait usage de la fermeture de nombres rationnels sous addition et la multiplication. Si 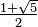 est rationnel, puis
est rationnel, puis  est aussi rationnelle, qui est une contradiction si elle est d??j?? connu que la racine carr??e d'un non- carr?? nombre naturel est irrationnel.
est aussi rationnelle, qui est une contradiction si elle est d??j?? connu que la racine carr??e d'un non- carr?? nombre naturel est irrationnel.
Autres formes

La formule φ = 1 + 1 / φ peut ??tre ??tendu de mani??re r??cursive pour obtenir un fraction continue pour le nombre d'or:
et son inverse:
Le convergents de ces fractions continues (1/1, 2/1, 3/2, 5/3, 8/5, 13/8, ..., ou 1/1, 1/2, 2/3, 3/5 , 5/8, 8/13, ...) sont des ratios de successives nombres de Fibonacci .
L'??quation φ 2 = 1 + φ produit m??me l'continu?? racine carr??e ou sourde infinie, la forme:
Une s??rie infinie peut ??tre d??riv?? d'exprimer phi:
??galement:
Ils correspondent au fait que la longueur de la diagonale d'un pentagone r??gulier est φ fois la longueur de son c??t??, et des relations similaires dans un pentagramme.
G??om??trie
Le nombre φ tourne fr??quemment dans la g??om??trie , en particulier dans les chiffres avec pentagonale sym??trie . La longueur d'un r??guli??re Pentagone diagonale est temps de φ son c??t??. Les sommets d'un r??guli??re icosa??dre sont ceux de trois mutuellement orthogonal rectangles d'or.
Il est connu g??n??rale algorithme d'organiser un certain nombre de n??uds uniform??ment sur une sph??re, pour l'un de plusieurs d??finitions de la distribution uniforme (voir, par exemple, Probl??me Thomson). Cependant, des r??sultats utiles d'approximation de diviser la sph??re en bandes parall??les de l'??galit?? de la zone et en pla??ant un noeud dans chaque bande ?? longitudes espac??es par une section d'or du cercle, soit 360 ?? / φ ≅ 222,5 ??. Cette m??thode a ??t?? utilis??e pour organiser les miroirs 1500 de l'??tudiant-participative satellite Starshine-3.
Division d'un segment de ligne
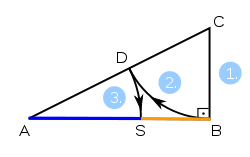
Ce qui suit algorithme produit une construction g??om??trique qui divise une segment de ligne en deux segments de ligne o?? le rapport entre la plus courte pour le segment de ligne est le nombre d'or:
- Avoir un segment AB, construire un BC perpendiculaire au point B, avec BC moiti?? de la longueur de AB. Dessinez le hypot??nuse AC.
- Tracez un cercle de centre C et de rayon BC. Ce cercle coupe l'hypot??nuse AC au point D.
- Tracez un cercle de centre A et de rayon AD. Ce cercle coupe le segment de ligne originale AB au point S. Point S divise le segment d'origine AB en segments de ligne AS et SB avec des longueurs dans le nombre d'or.
Triangle d'or, pentagone et pentagramme

Triangle d'or
Le triangle d'or peut ??tre caract??ris?? comme un triangle isoc??le ABC avec la propri??t?? que bissectrice de l'angle C produit un nouveau triangle CXB qui est un triangle semblable ?? l'original.
Si l'angle α = BCX, puis XCA = α en raison de la dichotomie, et CAB = α cause des triangles semblables; ABC = 2α de la sym??trie isoc??le originale et BXC = 2α par similarit??. Les angles d'un triangle se additionnent ?? 180 ??, de sorte 5α = 180, ce qui donne α = 36 ??. Ainsi, les angles du triangle d'or sont donc 36 ?? -72 ?? -72 ??. Les angles du triangle isoc??le reste obtus AXC (parfois appel?? le gnomon or) sont 36 ?? -36 ?? -108 ??.
Supposons XB a une longueur de 1, et nous appelons longueur de BC φ. En raison de la triangles isoc??les XC = XA et BC = XC, ce sont donc aussi la longueur φ. Longueur AC = AB, est donc ??gale ?? φ + 1. Mais triangle ABC est semblable ?? triangle CXB, afin AC / BC = BC / BX, et ainsi de AC est aussi ??gale ?? φ 2. Ainsi φ 2 = φ + 1, confirmant que φ est en effet le nombre d'or.
De m??me, le rapport de l'aire du triangle plus grand au plus petit AXC CXB est ??gal ?? φ, alors que le raison inverse est φ - 1.
Pentagone
Dans un pentagone r??gulier le rapport entre un c??t?? et une diagonale est 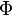 (Ce est ?? dire 1 / φ), tandis que d'intersection des diagonales de l'autre section dans le nombre d'or.
(Ce est ?? dire 1 / φ), tandis que d'intersection des diagonales de l'autre section dans le nombre d'or.
La construction d'Odom


George Odom a donn?? une construction remarquablement simple pour φ impliquant un triangle ??quilat??ral: si un triangle ??quilat??ral est inscrit dans un cercle et le segment de ligne joignant les milieux de deux c??t??s est produit ?? couper le cercle dans l'un des deux points, puis ces trois points sont en proportion dor??e. Ce r??sultat est la cons??quence directe de la intersection accords Th??or??me et peuvent ??tre utilis??s pour construire un pentagone r??gulier, une construction qui a attir?? l'attention du g??om??tre canadienne not?? HSM Coxeter qui l'a publi?? au nom de Odom comme un diagramme dans le American Mathematical Monthly accompagn?? par le seul mot ??Voil??!"
Pentacle

Le nombre d'or joue un r??le important dans la g??om??trie de pentagrammes. Chaque intersection des sections bords autres bords dans le nombre d'or. En outre, le rapport entre la longueur du segment plus court au segment d??limit?? par les deux bords se croisent (un c??t?? du pentagone dans le centre de la pentagone) est φ, que les quatre couleurs d'illustrations spectacles.
Le pentagramme comprend dix triangles isoc??les : cinq aigu?? et cinq obtus triangles isoc??les. Dans chacun d'eux, le rapport entre le c??t?? le plus long au c??t?? le plus court est φ. Les triangles aigus sont triangles d'or. Les triangles isoc??les sont obtus gnomons or.
Th??or??me de Ptol??m??e

Les propri??t??s de Golden Ratio d'un pentagone r??gulier peuvent ??tre confirm??s par l'application Le th??or??me de Ptol??m??e au quadrilat??re form?? par ??limination d'un de ses sommets. Si bord long et diagonales du quadrilat??re sont B, et les bords courts sont un, puis le th??or??me de Ptol??m??e donne 2 b = a + ab 2 qui rendements
Scalenity de triangles
Consid??rons un triangle dont les longueurs a, b et c dans l'ordre d??croissant. D??finir le "scalenity" du triangle d'??tre la plus petite des deux rapports a / b et b / c. Le scalenity est toujours inf??rieur ?? φ et peut ??tre faite aussi proche que d??sir?? ?? φ.
Triangle dont les c??t??s forment une progression g??om??trique
Si les longueurs des c??t??s d'un triangle forme une progression g??om??trique et sont dans le rapport 1: r: r 2, o?? r est le rapport commun, alors R doit ??tre comprise dans l'intervalle φ-1 <r <φ, ce qui est une cons??quence de la in??galit?? triangulaire (la somme de tous les deux c??t??s d'un triangle doit ??tre strictement plus grande que la longueur du troisi??me c??t??). Si r = φ alors les deux parties sont plus courtes 1 et φ, mais leur somme est φ 2, ainsi r <φ. Un calcul similaire montre que r> φ-1. Un triangle dont les c??t??s sont dans un rapport de 1: √φ: φ est un triangle rectangle (parce que 1 + φ = φ 2) connu en tant que Kepler triangle.
Triangle d'or, losange, et losange triaconta??dre
Un losange or est un losange dont les diagonales sont dans le rapport d'or. Le triaconta??dre est un losange polytope convexe qui poss??de une propri??t?? tr??s sp??ciale: toutes ses faces sont des losanges d'or. Dans le losange triaconta??dre la di??dre entre deux losanges adjacente est de 144 ??, ce qui est deux fois l'angle isoc??le d'un triangle d'or et quatre fois son angle le plus aigu.
Relation ?? la s??quence de Fibonacci
Les math??matiques du nombre d'or et de la suite de Fibonacci sont intimement li??s. La suite de Fibonacci est:
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ....
Le Solution de forme ferm??e (connue sous le nom La formule de Binet, m??me si elle ??tait d??j?? connue par Abraham de Moivre) pour la s??quence de Fibonacci implique le nombre d'or:

Le nombre d'or est le limite des ratios de mandats successifs de la suite de Fibonacci (ou ne importe quelle s??quence de Fibonacci comme), comme indiqu?? ?? l'origine par Kepler :
Par cons??quent, si un nombre de Fibonacci est divis??e par son pr??d??cesseur imm??diat dans la s??quence, le quotient se rapproche φ; par exemple, 987/610 ≈ 1,6180327868852. Ces approximations sont alternativement inf??rieur et sup??rieur ?? φ, et convergent sur φ que le nombre augmente de Fibonacci, et:
Plus g??n??ralement:
o?? ci-dessus, les ratios de mandats cons??cutifs de la suite de Fibonacci, est un cas o?? 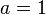 .
.
En outre, les puissances successives de φ ob??issent ?? la Fibonacci r??currence:
Cette identit?? permet ?? ne importe quel polyn??me φ ?? ??tre r??duite ?? une expression lin??aire. Par exemple:
Cependant, ce ne est pas de propri??t?? particuli??re de φ, parce que toute solution polyn??mes en x pour une ??quation quadratique peut ??tre r??duit d'une mani??re analogue, en appliquant:
pour les coefficients donnés un , b de telle sorte que x satisfait à l'équation. Même plus généralement, toute fonction rationnelle (à coefficients rationnels) de la racine d'une irréductible n e-polynôme de degré sur les rationnels peut être réduite à un polynôme de degré n - 1. Formulé en termes de théorie des champs, si ?? est une racine d'une irréductible n e-polynôme de degré, alors  est de degré n plus
est de degré n plus  , avec base
, avec base 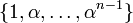 .
.
Symétries
Le nombre d'or et le ratio or inverse 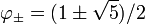 ont un ensemble de symétries qui préservent et interrelation entre eux. Ils sont tous deux conservés par les transformations linéaires fractionnaires
ont un ensemble de symétries qui préservent et interrelation entre eux. Ils sont tous deux conservés par les transformations linéaires fractionnaires  - ce fait correspond à l'identité et à la définition équation quadratique. En outre, ils sont échangés par les trois cartes
- ce fait correspond à l'identité et à la définition équation quadratique. En outre, ils sont échangés par les trois cartes  - ils sont inverses, symétriques par rapport à
- ils sont inverses, symétriques par rapport à 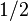 , et (projectivement) symétrique par rapport à deux.
, et (projectivement) symétrique par rapport à deux.
Plus profondément, ces cartes forment un sous-groupe dugroupe modulaire isomorphe augroupe symétrique sur 3 lettres,
isomorphe augroupe symétrique sur 3 lettres,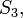 correspondant à lastabilisation de l'ensemble
correspondant à lastabilisation de l'ensemble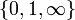 de 3 points standard sur ladroite projective, et les symétries correspondent à la carte de quotient
de 3 points standard sur ladroite projective, et les symétries correspondent à la carte de quotient - le sous-groupe
- le sous-groupe constitué de les 3 et cycles et de l'identité
constitué de les 3 et cycles et de l'identité fixe les deux chiffres, tandis que les 2-cycles échangent entre eux, réalisant ainsi la carte.
fixe les deux chiffres, tandis que les 2-cycles échangent entre eux, réalisant ainsi la carte.
Autres propri??t??s
Le nombre d'or a le plus simple expression (et plus lente convergence) comme un développement en fraction continue de tout nombre irrationnel (voir formes alternatives ci-dessus). Il est, pour cette raison, l'un des pires cas de rapprochement le théorème de Lagrange et il est un cas extrémal de l' inégalité Hurwitz pour approximations diophantiennes. Cela peut être la raison pour laquelle les angles proche du ratio or montrent souvent dans phyllotaxie (la croissance des plantes).
Le polynôme quadratique définition et la relation conjugué plomb en valeurs décimales qui ont leur partie fractionnaire en commun avec ??:
La séquence des pouvoirs de ?? contient ces valeurs 0.618 ..., 1.0, ... 1.618, 2.618 ...; plus généralement, toute la puissance de ?? est égal à la somme des deux puissances précédant immédiatement:
En conséquence, on peut facilement se décomposer toute puissance de ?? en un multiple de ?? et une constante. Le multiple et la constante sont toujours des nombres de Fibonacci adjacentes. Cela conduit à une autre propriété des puissances positives de ??:
Si  , Puis:
, Puis:
Lorsque le nombre d'or est utilisé comme base d'unsystème numérique(voirla base du rapport d'or, parfois surnomméphinaryou??-naire), tout entier a une représentation de terminaison, en dépit ?? étant irrationnel, mais chaque fraction a une représentation non-terminaison.
Le nombre d'or est uneunité fondamentale ducorps de nombres algébriques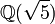 et est unnombre de Pisot-Vijayaraghavan. Sur le terrain
et est unnombre de Pisot-Vijayaraghavan. Sur le terrain 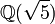 nous avons
nous avons O??
O?? 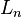 est le
est le  ièmenombre Lucas.
ièmenombre Lucas.
Le nombre d'or figure également à lagéométrie hyperbolique, comme la distance maximale entre un point situé sur un côté d'untriangle idéal à la plus proche des deux autres côtés: cette distance, la longueur du côté dutriangle équilatéral formé par les points de tangence d'un cercle inscrit dans le triangle idéal, est de 4 ln ??.
Développement décimal
Développement décimal du rapport d'or peut être calculé directement à partir de l'expression
avec ???5 ??? 2,2360679774997896964. Le racine carrée de 5 peut être calculé avec laméthode de Babylone, à commencer par une estimation initiale telle quex?? = 2 etitération
pourn= 1, 2, 3, ..., jusqu'à ce que la différence entrexnetx n-1devient égale à zéro, pour le nombre désiré de chiffres.
L'algorithme de Babylone pour ???5 est équivalente à la méthode de Newton pour résoudre l'équation x 2 - 5 = 0. Dans sa forme la plus générale, la méthode de Newton peut être appliqué directement à une équation algébrique, y compris l'équation x 2 - x - 1 = 0 qui définit le nombre d'or. Cela donne une itération qui converge vers le nombre d'or lui-même,
pour une première estimation appropriéx?? tel quex= ?? 1. Procédé légèrement plus rapide consiste à réécrire l'équationx- 1 - 1 /x= 0, auquel cas l'itération de Newton devient
Ces itérations tous convergent quadratique; qui est, chaque étape double à peu près le nombre de chiffres corrects. Le nombre d'or est donc relativement facile de calculer avec précision arbitraire. Le temps nécessaire pour calculer n chiffres du nombre d'or est proportionnelle au temps nécessaire pour diviser deux n nombres à chiffres. Ceci est considérablement plus rapide que les algorithmes connus pour les nombres transcendants ?? et e .
Une alternative facile à programmer en utilisant uniquement arithmétique entière est de calculer deux grands nombres de Fibonacci consécutifs et les diviser. Le ratio de Fibonacci numéros F 25001 et F 25000 , chaque plus de 5000 chiffres, les rendements de plus de 10.000 chiffres significatifs de la proportion dorée.
Le nombre d'or ?? a été calculé avec une précision de plusieurs millions de chiffres décimaux (séquence A001622 dans OEIS ). Alexis Irlande effectué les calculs et la vérification des 17000000000 premiers chiffres.
Pyramides
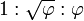 et
et 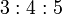 et
et 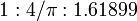 sont d'un intérêt particulier par rapport aux pyramides égyptiennes.
sont d'un intérêt particulier par rapport aux pyramides égyptiennes. Les deux pyramides égyptiennes et les mathématiques régulierspyramides carrées qui leur ressemblent peuvent être analysés par rapport au nombre d'or et d'autres ratios.
Pyramides et triangles mathématiques
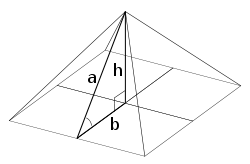
Une pyramide dans laquelle le apothème (hauteur oblique le long de la bissectrice d'un visage) est égal à ?? fois la semi-base (la largeur de base de la moitié) est parfois appelé une pyramide d'or . Le triangle isocèle qui est le visage d'une telle pyramide peut être construite à partir des deux moitiés d'un rectangle d'or diagonale diviser (de taille semi-base en apothème), reliant les bords de longueur moyenne pour faire le apothème. La hauteur de cette pyramide est  fois la semi-base (qui est, la pente de la face est
fois la semi-base (qui est, la pente de la face est  ); le carré de la taille est égale à la surface d'un visage, ?? fois le carré de la semi-base.
); le carré de la taille est égale à la surface d'un visage, ?? fois le carré de la semi-base.
La médianetriangle de la pyramide "d'or" (voir schéma), avec des côtés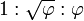 est intéressant dans son propre droit, démontrant par lethéorème de Pythagorela relation
est intéressant dans son propre droit, démontrant par lethéorème de Pythagorela relation ou
ou  . Cette " Kepler triangle "est la seule proportion de triangle avec des longueurs de pointe enprogression géométrique, tout comme le 3-4-5 triangle est la seule partie de triangle rectangle avec des longueurs de bord enprogression arithmétique. L'angle de tangente
. Cette " Kepler triangle "est la seule proportion de triangle avec des longueurs de pointe enprogression géométrique, tout comme le 3-4-5 triangle est la seule partie de triangle rectangle avec des longueurs de bord enprogression arithmétique. L'angle de tangente correspond à l'angle que du côté de la pyramide fait par rapport à la masse, ... 51,827 degrés (51 ° 49 ' 38 ").
correspond à l'angle que du côté de la pyramide fait par rapport à la masse, ... 51,827 degrés (51 ° 49 ' 38 ").
Une forme de pyramide à peu près semblable, mais avec des proportions raisonnables, est décrite dans le Papyrus Mathématique Rhind (la source d'une grande partie de la connaissance moderne de l'antique égyptienne mathématiques), sur la base du 3: 4: 5 triangle; la pente de face correspondant à l'angle avec la tangente 4/3 est 53,13 degrés (53 degrés et 8 minutes). La hauteur de la pente ou apothème est 5/3 ou 1.666 ... fois la semi-base. Le papyrus Rhind a un autre problème de la pyramide ainsi, encore une fois avec une pente rationnelle (exprimé en terme de trop lever). Mathématiques égyptiennes ne comprennent pas la notion des nombres irrationnels, et la pente inverse rationnelle (run / hausse, multiplié par un facteur de 7 à convertir leurs unités conventionnelles de palmiers par coudée) a été utilisé dans la construction des pyramides.
Un autre pyramide mathématique avec des proportions à peu près identiques à la "golden" un est celui qui périmètre égal à 2?? fois la hauteur, ou h: b = 4: ??. Ce triangle a un angle de face de 51,854 ° (51 ° 51 '), très proche de la 51,827 ° de la Kepler triangle. relation Cette pyramide correspond à la relation fortuite  .
.
Pyramides égyptiennes très proches en proportion de ces pyramides mathématiques sont connus.
Pyramides ??gyptiennes
Dans le milieu du XIXe siècle, Röber étudié diverses pyramides égyptiennes, y compris Khéphren, Mykérinos et certains de Gizeh, Saqqarah, et ??????les groupes Abousir, et a été interprété comme disant que la moitié de la base du côté de la pyramide est le moyen milieu du côté , formant ce que d'autres auteurs identifiés comme triangle Kepler; beaucoup d'autres théories mathématiques de la forme des pyramides ont également été explorées.
Une pyramide égyptienne est remarquablement proche d'une «pyramide d'or" -la Grande Pyramide de Gizeh (aussi connu comme la pyramide de Khéops ou Khufu). Sa pente de 51 ° 52 'est très proche de la pyramide "or" inclinaison de 51 ° 50' et la pyramide inclinaison base de ??-de 51 ° 51 '; autres pyramides de Gizeh (Khéphren, 52 ° 20 ', et Mykérinos, 50 ° 47') sont également tout près. Que la relation au nombre d'or dans ces pyramides est de par leur conception ou par accident reste ouvert à la spéculation. Plusieurs autres pyramides égyptiennes sont très proches au rationnel 3: 4: 5 forme.
Ajout de carburant à la controverse sur la paternité architecturale de la Grande Pyramide,Eric Temple Bell, mathématicien et historien, a affirmé en 1950 que les mathématiques égyptiennes auraient pas appuyé la possibilité de calculer la hauteur de la pente des pyramides, ou le rapport à la hauteur, à l'exception dans le cas de la 3: 4: 5 pyramide, depuis le 3: 4: 5 triangle était le seul triangle connue des Egyptiens et ils ne savaient pas le théorème de Pythagore, ni aucune façon de raisonner sur irrationnels tels que ?? ou ?? .
Michael Rice, affirme que les autorités principales sur l'histoire de l'architecture égyptienne ont fait valoir que les Egyptiens connaissaient bien le nombre d'or et qu'il fait partie des mathématiques des Pyramides, citant Giedon (1957). Les historiens de la science ont toujours débattu pour savoir si les Égyptiens avaient des connaissances ou pas, soutenant plutôt que son apparition dans un bâtiment égyptien est le fruit du hasard.
En 1859, l' pyramidologist John Taylor a affirmé que, dans la Grande Pyramide de Gizeh , le nombre d'or est représenté par le rapport de la longueur de la face (la hauteur de la pente), inclinée à un angle ?? à la terre, à la moitié de la longueur du côté de la base carrée, équivalente à la sécante de l'angle ??. Les deux longueurs supérieures étaient d'environ 186,4 et 115,2 mètres respectivement. Le rapport de ces longueurs est le nombre d'or, précis à plus de chiffres que l'une des mesures originales. De m??me, Howard Vyse, selon Matila Ghyka, a rapporté la grande hauteur de la pyramide 148,2 m, et la demi-base de 116,4 m, ce qui donne 1.6189 pour le rapport de hauteur inclinée à demi-base, encore plus précis que la variabilité des données.
Observations contestées
Exemples d'observations litigieuses de la proportion dorée sont les suivants:
- L'historien John Homme stipule que les pages de la Bible de Gutenberg ont été "basées sur la forme de la section d'or". Toutefois, selon les propres mesures de l'homme, le rapport de hauteur à largeur est de 1,45.
- Certaines proportions spécifiques dans les corps de nombreux animaux (y compris les humains) et des parties de coquilles de mollusques et céphalopodes sont souvent prétendu être dans le nombre d'or. Il ya une grande variation dans les mesures réelles de ces éléments dans des individus spécifiques, cependant, et la proportion en question est souvent très différente de la proportion dorée. Le ratio des os phalanges successives des chiffres et l'os métacarpien a été dit de rapprocher le nombre d'or. Le nautile, la construction de ce qui se déroule dans une spirale logarithmique, est souvent cité, généralement avec l'idée que toute spirale logarithmique est lié à le nombre d'or, mais parfois avec l'affirmation selon laquelle chaque nouvelle chambre est proportionné par le nombre d'or par rapport à la précédente; Toutefois, les mesures de coquilles de nautilus ne supportent pas cette prétention.
- Les proportions des différents composants de l'installation (nombre de feuilles à branches, des diamètres de figures géométriques à l'intérieur des fleurs) sont souvent réclamés pour montrer le rapport proportion d'or dans plusieurs espèces. Dans la pratique, il existe des variations importantes entre les individus, les variations saisonnières et des variations d'âge de ces espèces. Bien que le nombre d'or peut être trouvée dans des proportions chez certaines personnes à des moments particuliers dans leur cycle de vie, il n'y a pas de rapport constant dans leurs proportions.
- En investissant, certains praticiens de l'analyse technique utilisent le nombre d'or pour indiquer le soutien d'un niveau de prix, ou de la résistance aux augmentations de prix, d'un stock ou d'une marchandise; après prix significative change haut ou le bas, de nouveaux supports et résistances sont censément trouvé à ou près de prix liés au prix de départ par le nombre d'or. L'utilisation du nombre d'or dans l'investissement est également liée à des modèles plus compliqués décrits par les nombres de Fibonacci (par exemple principe de l'onde d'Elliott et de retracement de Fibonacci). Cependant, d'autres analystes du marché ont publié des analyses suggérant que ces pourcentages et les modèles ne sont pas étayées par les données.


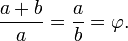
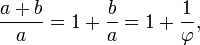

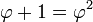

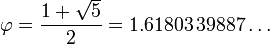
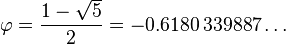
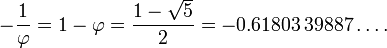

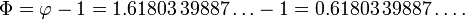
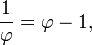
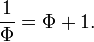

![\ Varphi = [1; 1, 1, 1, \ dots] = 1 + \ cfrac {1} {1 + \ cfrac {1} {1 + \ cfrac {1} {1 + \ ddots}}}](../../images/2794/279449.png)
![\ Varphi ^ {- 1} = [0; 1, 1, 1, \ dots] = 0 + \ cfrac {1} {1 + \ cfrac {1} {1 + \ cfrac {1} {1 + \ ddots}}}](../../images/2794/279450.png)


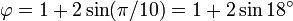

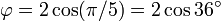

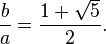


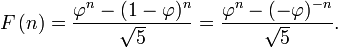
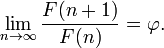
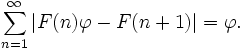
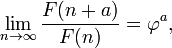

![\ Begin {align} 3 \ varphi ^ 3-5 \ varphi ^ 2 + 4 = 3 & (\ varphi ^ 2 + \ varphi) - 5 \ varphi ^ 2 + 4 = \\ & 3 [(\ varphi + 1) + \ varphi] - 5 (\ varphi + 1) + 4 = \\ & \ varphi + 2 \ environ 3,618. \ End {align}](../../images/2795/279500.png)