Cube
Contexte des ??coles Wikip??dia
SOS Enfants, qui se d??roule pr??s de 200 sos ??coles dans le monde en d??veloppement, a organis?? cette s??lection. enfants SOS est le plus grand don de charit?? du monde enfants orphelins et abandonn??s la chance de la vie familiale.
| Hexahedron r??guli??re | |
|---|---|
 (Cliquez ici pour le mod??le de rotation) | |
| Type | Solide de Platon |
| ??l??ments | F = 6, E = 12 V = 8 (χ 2 =) |
| Faces de c??t??s | 6 {4} |
| Symbole Schl??fli | {4,3} |
| Symbole de Wythoff | 3 | 2 4 |
| Coxeter diagramme |     |
| Sym??trie | O h, 3 BC, [4,3], (432 *) |
| groupe de rotation | O, [4,3] +, (432) |
| R??f??rences | U 06, C 18, W 3 |
| Propri??t??s | R??gulier convexe zono??dre |
| Di??dre | 90 ?? |
 4.4.4 ( Vertex figure) |  Octa??dre ( poly??dre dual) |
 Net | |
En g??om??trie , un cube est un objet solide tridimensionnel d??limit?? par six carr??s visages, facettes ou sur les c??t??s, avec trois r??unions ?? chaque vertex. Le cube peut aussi ??tre appel?? un r??gulier hexa??dre et est l'un des cinq solides de Platon . Ce est un type sp??cial de la place prisme rectangulaire de et de parall??l??pip??de trap??zo??dre trigonale. Le cube est double ?? l' octa??dre . Il a une sym??trie cubique (??galement appel?? sym??trie octa??drique). Il est sp??cial en ??tant un et un cubo??de rhombo??dre.
Projections orthogonales
Le cube a quatre sp??ciales projections orthogonales, centr??es sur un sommet, bords, le visage et normales ?? son Figure sommet. La premi??re et la troisi??me correspond ?? l'A 2 et B 2 Avions Coxeter.
| Centr?? par | Visage | Sommet |
|---|---|---|
| Avions Coxeter | B 2 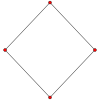 | A 2  |
| Projective sym??trie | ||
| Vues inclin??es |  |  |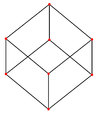
Les coordonn??es cart??siennes
Pour un cube centr?? ?? l'origine, avec des bords parall??les aux axes et avec une longueur d'ar??te de 2, les coordonn??es cart??siennes des sommets sont
- (?? 1, ?? 1, ?? 1)
tandis que l'int??rieur est constitu?? de l'ensemble des points (x 0, x 1, x 2) ?? -1 <x i <1.
??quation dans R 3
Dans la g??om??trie analytique , la surface d'un cube de centre (x 0, y 0, z 0) et la longueur de bord de la figure 2a est la lieu des points (x, y, z) de telle sorte que
Formules
Pour un cube de longueur d'ar??te 
,
| Surface |  |
| volume |  |
| face ?? la diagonale |  |
| l'espace en diagonale |  |
| rayon de sph??re circonscrite |  |
| rayon de sph??re tangente aux bords |  |
| rayon de sph??re inscrite |  |
| les angles entre les faces (en radians ) |  |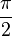
Comme le volume d'un cube est la puissance trois de ses c??t??s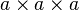 
, puissances tierces sont appel??s cubes, par analogie avec places et deuxi??me puissances.
Un cube a le plus grand volume entre parall??l??pip??des (bo??tes rectangulaires) avec une donn??e surface. En outre, un cube a le plus grand volume entre parall??l??pip??des avec la m??me taille totale lin??aire (longueur + largeur + hauteur).
Colorations uniformes et la sym??trie
Le cube a trois colorations uniformes, nomm??s par les couleurs des faces carr??es autour de chaque sommet: 111, 112, 123.
Le cube a trois classes de sym??trie, qui peuvent ??tre repr??sent??s par sommet-transitif colorer les visages. La plus haute sym??trie octa??drique O h a tous les visages de la m??me couleur. Le 4h sym??trie di??dre D provient du cube ??tant un prisme, avec les quatre c??t??s ??tant de la m??me couleur. Le plus bas 2h sym??trie D est ??galement une sym??trie prismatique, avec des couleurs alternant les c??t??s, il ya donc trois couleurs, appari??s par les c??t??s oppos??s. Chaque forme de sym??trie a une autre Symbole de Wythoff.
| Nom | Hexa??dre r??gulier | Carr?? prisme | Cubo??de | Trigone trap??zo??dre |
|---|---|---|---|---|
| Coxeter-Dynkin |     |  | | |
| Symbole Schl??fli | {4,3} | {4} {x} | {} X {} {} ?? | |
| Symbole de Wythoff | 3 | 4 2 | 4 2 | 2 | 2 2 2 | | |
| Sym??trie | O h (* 432) | 4h D (* 422) | 2h D (* 222) | D 3d (2 * 3) |
| Sym??trie d'ordre | 24 | 16 | 8 | 12 |
| Image (Coloration uniforme) |  (111) |  (112) |  (123) |  (111), (112), (122) et (222) |
Relations g??om??triques
Un cube a onze filets (illustration ci-dessus): Ce est, il existe des moyens onze pour aplatir un cube creux en coupant sept bords. Pour colorer le cube de sorte que deux faces adjacentes ont la m??me couleur, il faudrait au moins trois couleurs.
Le cube est la cellule de la seule carrelage r??guli??re de l'espace euclidien ?? trois dimensions. Il est ??galement unique parmi les solides de Platon en ayant des faces avec un nombre pair de c??t??s et, par cons??quent, il est le seul membre de ce groupe qui est un zono??dre (chaque visage a un point de sym??trie).
Le cube peut ??tre d??coup?? en six identique pyramides carr??es. Si ces pyramides carr??es sont ensuite fix??es sur les faces d'un second cube, un dod??ca??dre rhombique est obtenu (avec des paires de triangles coplanaires combin??s en losange visages.)
Autres dimensions
L'analogue d'un cube en quatre dimensions espace euclidien a un nom-a sp??ciale tesseract ou hypercube. Plus correctement, un hypercube (ou n cube de dimension ou simplement -Cube n) est l'analogue du cube dans l'espace de dimension n euclidienne et un tesseract est ?? l'ordre quatre-hypercube. Un hypercube est aussi appel?? une mesure polytope.
Il existe des analogues du cube des dimensions inf??rieures aussi: un point de dimension 0, un segment dans une dimension et un carr?? en deux dimensions.
Poly??dres connexes
Le quotient du cube par le carte donne un antipode poly??dre projective, le h??micube.
Si le cube d'origine a une longueur de bord, son poly??dre dual (un octa??dre ) a une longueur de bord 
.
Le cube est un cas particulier dans diff??rentes classes de poly??dres g??n??rale:
| Nom | Pointe-longueurs ??gales? | L'??galit?? des angles? | Angle droit? |
|---|---|---|---|
| Cube | Oui | Oui | Oui |
| Rhombo??dre | Oui | Oui | Aucun |
| Cubo??de | Aucun | Oui | Oui |
| Parall??l??pip??de | Aucun | Oui | Aucun |
| hexa??dre quadrilat??re face | Aucun | Aucun | Aucun |
Les sommets d'un cube peuvent ??tre regroup??s en deux groupes de quatre, formant chacun une r??guli??re t??tra??dre ; plus g??n??ralement ce est consid??r?? comme un demicube. Ces deux forment ensemble un r??guli??re compos??, la stella octangula. L'intersection des deux formes d'un octa??dre r??gulier. Les sym??tries d'un t??tra??dre r??gulier correspondent ?? celles d'un cube dont chaque t??tra??dre de la carte elle-m??me; les autres sym??tries du cube carte les deux ?? l'autre.
Un tel t??tra??dre r??gulier a un volume de 1/2 de celle du cube. L'espace restant est constitu?? de quatre t??tra??dres irr??guliers avec un volume ??gal de 1/6 de celle du cube, chaque.
Le cube redress?? est le cubocta??dre. Si les petits coins sont coup??s nous obtenons un poly??dre ?? six faces octogonales et huit triangulaires. En particulier, nous pouvons obtenir des octogones r??guliers ( cube tronqu??). Le rhombicubocta??dre est obtenu en coupant les coins et les bords de la quantit?? correcte.
Un cube peut ??tre inscrite dans un dod??ca??dre sorte que chaque sommet du cube est un sommet du dod??ca??dre et chaque bord est une diagonale de l'un des visages de la dod??ca??dre; prendre tous les cubes donne lieu au compos?? de cinq cubes r??guliers.
Si deux coins oppos??s d'un cube sont limit??s ?? la profondeur des trois sommets directement li??s ?? eux, un octa??dre irr??gulier est obtenu. Huit de ces octa??dres irr??guli??re peut ??tre fix?? aux faces triangulaires d'un octa??dre r??gulier pour obtenir le cubocta??dre.
Le cube est topologiquement li?? ?? une s??rie de poly??dres et pavages sph??rique pour-3 chiffres sommet.
| Poly??dres | Euclidienne | Pavages hyperboliques | ||||||
|---|---|---|---|---|---|---|---|---|
 {2,3} |  {3,3} |  {4,3} |  {5,3}  |  {6,3}  |  {7,3}  |  {8,3}  | ... |  (∞, 3}  |
Le cubocta??dre est une d'une famille de poly??dres uniformes li??es au cube et l'octa??dre r??gulier.
| Sym??trie: [4,3], (432 *) | [4,3] +, (432) | [1 + 4,3], (332 *) | [4,3 +], (3 * 2) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| | | | | | | |  | | |
 |  |  |  |  |  |  |  |  |  |
| {4,3} | 0,1 t {4,3} | t 1} {4,3 | 1,2 t {4,3} | {3,4} | 0,2 t {4,3} | t {4,3} 0,1,2 | s {4,3} | h {4,3} | h 1,2 {} 4,3 |
| Jumelage ?? poly??dres uniformes | |||||||||
 | | | | | | |  | | |
 |  |  |  |  |  |  |  |  |  |
| V4.4.4 | V3.8.8 | V3.4.3.4 | V4.6.6 | V3.3.3.3 | V3.4.4.4 | V4.6.8 | V3.3.3.3.4 | V3.3.3 | V3.3.3.3.3 |
Le cube est topologiquement li?? en tant que partie de la s??quence de pavages r??guliers, se ??tendant dans le plan hyperbolique: {4, p}, p = 3,4,5 ...
| {4,3} |  {4,4} |  {4,5} |  {4,6} |  {4,7} |  {4,8} | ... |  {4, ∞} |
Avec sym??trie di??dre, Dih 4, le cube est li??e topologiquement ?? une s??rie de poly??dres uniforme et pavages 4.2n.2n, se ??tendant dans le plan hyperbolique:
| Sym??trie * N42 [N, 4] | Sph??rique | Euclidienne | Hyperbolique ... | |||||
|---|---|---|---|---|---|---|---|---|
| * 242 [2,4] 4h D | * 342 [3,4] O h | * 442 [4,4] P4m | * 542 [5,4] | * 642 [6,4] | * 742 [7,4] | * 842 [8,4] ... | * ∞42 [∞, 4] | |
| Tronqu?? chiffres |  4.4.4 |  4.6.6 |  4.8.8 |  4.10.10 |  4.12.12 |  14/04/14 |  16/04/16 |  4.∞.∞ |
| Coxeter Schl??fli | 1,2 t {4,2} | 1,2 t {4,3} | 1,2 t {4,4} | 1,2 t {4,5} | 1,2 t {4,6} | 1,2 t {4,7} | 1,2 t {4,8} | 1,2 t {4, ∞} |
| Chiffres double uniformes | ||||||||
| n-Kis chiffres |  V4.4.4 | V4.6.6 |  V4.8.8 |  V4.10.10 |  V4.12.12 |  V4.14.14 |  V4.16.16 |  V4.∞.∞ |
| Coxeter | | | | | | | | |
Tous ces chiffres ont sym??trie octa??drique.
Le cube est une partie d'une s??quence de pavages et poly??dres rhombiques avec [n, 3] Coxeter groupe sym??trie. Le cube peut ??tre consid??r??e comme un hexa??dre rhombique o?? les losanges sont des carr??s.
| Sym??trie * N32 [N, 3] | Sph??rique | Euclidienne | Pavage hyperbolique | ||||
|---|---|---|---|---|---|---|---|
| * 332 [3,3] T d | * 432 [4,3] O h | * 532 [5,3] I h | * 632 [6,3] p6m | * 732 [7,3] | * 832 [8,3] | * ∞32 [∞, 3] | |
| Quasiregular chiffres configuration |  3.3.3.3 |  3.4.3.4 |  3.5.3.5 |  3.6.3.6 |  3.7.3.7 |  3.8.3.8 |  3.∞.3.∞ |
| Coxeter diagramme | | | | | | | |
| Double (Losange) chiffres configuration | V3.3.3.3 | V3.4.3.4 |  V3.5.3.5 |  V3.6.3.6 |  V3.7.3.7 |  V3.8.3.8 |  V3.∞.3.∞ |
| Coxeter diagramme | | | | | | | |
Le cube est un prisme carr??:
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ... | ∞ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| | | | | | |  |  |  |  | | |
 | |  |  |  |  |  |  |  |  |  | |
| Comme poly??dres sph??riques | |||||||||||
 |  |  |  |  |  |  |  | ||||
Comme un trap??zo??dre trigonal, le cube est en relation avec la famille de sym??trie di??dre hexagonale.
| Sym??trie: [6,2], (622 *) | [6,2] +, (622) | [1 + 6,2], (322) | [6,2 +], (2 * 3) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| | | | | | | | | | |
 |  | |  |  |  | |  |  |  |
| {6,2} | 0,1 t {6,2} | t 1} {6,2 | 1,2 t {6,2} | t 2 {6,2} | 0,2 t {6,2} | t {6,2} 0,1,2 | s {6,2} | h {6,2} | h 1,2 {} 6,2 |
| Duals uniformes | |||||||||
| | | | | | | | | | |
| |  | |  | | |  |  | |  |
| V6 2 | V12 2 | V6 2 | V4.4.6 | V2 6 | V4.4.6 | V4.4.12 | V3.3.3.6 | V3 2 | V3.3.3.3 |
 Compos?? de trois cubes |  Compos?? de cinq cubes |
Dans alv??oles uniformes et polychora
Ce est un ??l??ment de 9 sur 28 convexe alv??oles uniformes:
| Nid d'abeille cubique | Tronqu?? nid d'abeille prismatique carr??e | Snub nid d'abeille prismatique carr??e | Allong??e nid d'abeille prismatique triangulaire | Gyroelongated nid d'abeille prismatique triangulaire |
 |  |  |  |  |
| Nid d'abeille cube Cantellated | Nid d'abeille cube Cantitruncated | Nid d'abeille cube Runcitruncated | Runcinated nid d'abeille cube altern??   | |
 |  |  |  |
Ce est aussi un ??l??ment de cinq ?? quatre dimensions polychora uniforme:
| Tesseract | Cantellated 16 cellules | Tesseract Runcinated | Cantitruncated 16 cellules | Runcitruncated 16 cellules |
 |  |  |  |  |
Cubes combinatoires
Un autre type de cube est le graphe de cube, qui est le graphe de sommets et d'ar??tes du cube g??om??trique. Ce est un cas particulier de la Hypercube.
Une extension est tridimensionnel k -aire Hamming graphique, qui, pour k = 2 est le graphique de cube. Graphiques de ce genre se produisent dans la th??orie de traitement parall??le dans les ordinateurs.
- Unit?? cube
- Tesseract
- Cube (film)
- Trap??zo??dre
- Yoshimoto Cube
- Le Cube (Game Show)
- Le cube de Prince Rupert
- Cube OLAP
- L??vheim cube d'??motion
- Cube de Heymans
- Cube de Necker
- Cube de Rubik
