
Alg??bre
Contexte des ??coles Wikip??dia
Cette s??lection se fait pour les ??coles par la charit?? pour enfants lire la suite . Une bonne fa??on d'aider d'autres enfants est de parrainer un enfant
L'alg??bre est une branche de math??matiques concernant l'??tude de la structure , relation et la quantit?? . Le nom est d??riv?? du trait?? ??crit en arabe par le Persan math??maticien, astronome, astrologue et g??ographe, Muhammad bin Musa al-Khwarizmi intitul?? Kitab al-Jabr wa-l-Muqabala (ce qui signifie " Abr??g?? du calcul par la restauration et la comparaison "), qui a fourni des op??rations symboliques pour la solution syst??matique de lin??aire et ??quations du second degr?? .
Avec la g??om??trie , l'analyse , la combinatoire et la th??orie des nombres , l'alg??bre est l'une des principales branches de math??matiques . alg??bre ??l??mentaire est souvent partie du programme d'??tudes dans l'enseignement secondaire et fournit une introduction aux id??es fondamentales de l'alg??bre, y compris les effets de l'ajout et de la multiplication num??ros , le concept de variables, d??finition des polyn??mes , avec factorisation et la d??termination de leur racines.
L'alg??bre est beaucoup plus large que l'alg??bre ??l??mentaire et peut ??tre g??n??ralis??e. En plus de travailler directement avec les nombres, l'alg??bre couvre travailler avec symboles, variables et ensemble ??l??ments. Addition et la multiplication sont consid??r??s comme g??n??rale op??rations, et leurs d??finitions pr??cises conduisent ?? des structures telles que des groupes , anneaux et domaines.
Classification
Alg??bre peut ??tre divis??e ?? peu pr??s dans les cat??gories suivantes:
- Alg??bre ??l??mentaire , dans lequel les propri??t??s des op??rations sur le syst??me des nombres r??els sont enregistr??s en utilisant des symboles comme des ??fictifs?? pour d??signer constantes et variables, et les r??gles r??gissant expressions math??matiques et ??quations impliquant ces symboles sont ??tudi??s (note que cela inclut g??n??ralement l'objet de cours appel?? alg??bre interm??diaire et l'alg??bre coll??ge), ??galement appel?? seconde ann??e et la troisi??me ann??e de l'alg??bre;
- Alg??bre abstraite , parfois aussi appel?? l'alg??bre moderne, dans laquelle les structures alg??briques tels que des groupes , anneaux et les champs sont axiomatique d??fini et ??tudi??; cela inclut, parmi d'autres domaines,
- Alg??bre lin??aire , dans lequel les propri??t??s sp??cifiques des espaces vectoriels sont ??tudi??s (y compris les matrices );
- Alg??bre universelle, dans laquelle les propri??t??s communes ?? toutes les structures alg??briques sont ??tudi??s.
- Th??orie alg??brique des nombres, dans laquelle les propri??t??s des nombres sont ??tudi??s ?? travers des syst??mes alg??briques. La th??orie des nombres beaucoup inspir??s de l'abstraction originale en alg??bre.
- G??om??trie alg??brique dans son aspect alg??brique.
- Combinatoire alg??brique , dans lequel les m??thodes alg??briques abstraits sont utilis??s pour ??tudier les questions combinatoires.
Dans certaines directions d'??tude avanc??e, les syst??mes axiomatiques alg??briques tels que des groupes, des bagues, des champs et des alg??bres sur un champ sont ??tudi??es en pr??sence d'un g??om??trique structure (un m??trique ou une topologie ) qui est compatible avec la structure alg??brique. La liste comprend un certain nombre de domaines analyse fonctionnelle:
- Espaces lin??aires norm??s
- Espaces de Banach
- Espaces de Hilbert
- Alg??bres de Banach
- Alg??bres norm??s
- Alg??bres topologiques
- Groupes topologiques
Alg??bre ??l??mentaire
Alg??bre ??l??mentaire est la forme la plus fondamentale de l'alg??bre. Il est enseign?? aux ??l??ves qui sont pr??sum??s ne pas avoir connaissance des math??matiques au-del?? des principes de base de l'arithm??tique . En arithm??tique, seuls les num??ros et leurs op??rations arithm??tiques (tels que +, -, ??, ??) se produire. En alg??bre, les nombres sont souvent d??sign??es par des symboles (par exemple, A, X ou Y). Ce est utile parce que:
- Il permet la formulation g??n??rale des lois arithm??tiques (tels que a + b = b + a pour tout a et b), et est donc la premi??re ??tape pour une exploration syst??matique des propri??t??s du syst??me des nombres r??els .
- Il permet la r??f??rence aux num??ros ??inconnus??, la formulation des ??quations et l'??tude de la fa??on de r??soudre ces (par exemple, "trouver un certain nombre x tel que x 3 + 1 = 10").
- Il permet la formulation de fonctionnels relations (tels que "Si vous vendez x billets, alors votre b??n??fice sera 3 x - 10 dollars, ou f (x) = x 3 - 10, o?? f est la fonction, et x est le nombre dans laquelle la fonction est appliqu??e. ??).
Polyn??mes
A est un polyn??me expression qui est construit ?? partir d'un ou plusieurs variables et constantes, en utilisant uniquement les op??rations d'addition, la soustraction et la multiplication (o?? la multiplication r??p??t??e de la m??me variable est en standard d??sign??s comme exponentiation avec tout un exposant de nombre positif constant). Par exemple, 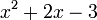 est un polyn??me dans la seule variable x.
est un polyn??me dans la seule variable x.
Une classe importante de probl??mes dans l'alg??bre est factorisation de polyn??mes, ce est l'expression d'un polyn??me donn?? en tant que produit d'autres polyn??mes. L'exemple ci-dessus peut polynomiale ??tre pris comme 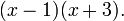 Une classe connexe de probl??mes est de trouver des expressions alg??briques pour le racines d'un polyn??me ?? une seule variable.
Une classe connexe de probl??mes est de trouver des expressions alg??briques pour le racines d'un polyn??me ?? une seule variable.
Alg??bre abstraite
Alg??bre abstraite ??tend les concepts familiers trouv??s dans l'alg??bre ??l??mentaire et l'arithm??tique des nombres ?? des concepts plus g??n??raux.
Sets: Plut??t que de simplement consid??rer les diff??rents types de num??ros , r??sum?? alg??bre offres avec la notion plus g??n??rale d'ensembles: une collection de tous les objets (appel?? ??l??ments) s??lectionn??s par la propri??t??, sp??cifiques pour l'ensemble. Toutes les collections des types familiers de nombres sont des ensembles. Autres exemples d'ensembles comprennent l'ensemble des deux-par-deux matrices , l'ensemble de tous second degr?? polyn??mes (AX 2 + bx + c), l'ensemble des deux dimensions vecteurs dans le plan, et les divers groupes finis tels que les groupes cycliques qui sont le groupe d'entiers modulo n. La th??orie des ensembles est une branche de la logique et pas techniquement une branche de l'alg??bre.
Les op??rations binaires: La notion de plus (+) est pr??lev??e pour donner une op??ration binaire, * dire. La notion de fonctionnement binaire est rien sans l'ensemble sur lequel l'op??ration est d??fini. Pour deux ??l??ments A et B dans un ensemble S a * b donne un autre ??l??ment dans le jeu; cette condition est appel??e . fermeture Addition (+), la soustraction (-), multiplication (??), et la division (??) peuvent ??tre des op??rations binaires lorsqu'elle est d??finie sur diff??rents ensembles, tout comme l'addition et la multiplication des matrices, vecteurs, et des polyn??mes.
??l??ments d'identit??: Les num??ros z??ro et un sont extraites de donner ?? la notion d'un ??l??ment d'identit?? pour une op??ration. Z??ro est l'??l??ment d'identit?? pour l'addition et on est l'??l??ment d'identit?? pour la multiplication. Pour un op??rateur binaire g??n??rale * l'identit?? ??l??ment e doit r??pondre ?? un e * = a et e * a = a. Cela vaut pour l'addition a + 0 = a 0 et a = a + et une multiplication ?? 1 = a 1 et a = a ??. Cependant, si nous prenons les nombres naturels positifs et plus, il n'y a aucun ??l??ment d'identit??.
??l??ments inverses: Les nombres n??gatifs donnent lieu ?? la notion d'??l??ments inverses. Par ailleurs, l'inverse d'une -a est, pour la multiplication et l'inverse est ??gal ?? 1 / a. Un ??l??ment inverse g??n??rale -1 doit satisfaire la propri??t?? qui a * a = -1 e et un -1 * a = e.
Associativit?? : Addition des entiers poss??de une propri??t?? appel??e associativit??. Cela signifie que le groupement des nombres ?? ajouter ne affecte pas la somme. Par exemple: (2 + 3) + 4 + 2 = (3 + 4). En g??n??ral, cela devient (a * b) * c = a * (b * c). Cette propri??t?? est partag??e par la plupart des op??rations binaires, mais pas la soustraction ou division ou octonion multiplication.
Commutativit?? : Addition des entiers a ??galement une propri??t?? appel??e commutativit??. Autrement dit, l'ordre des num??ros ?? ajouter ne affecte pas la somme. Par exemple: 2 + 3 = 3 + 2. En g??n??ral, cela devient un * b * b = a. Seules quelques op??rations binaires ont cette propri??t??. Il est valable pour les nombres entiers avec addition et de multiplication, mais il ne tient pas pour la multiplication de matrices ou multiplication quaternionique.
Groupes-structures d'un ensemble avec une op??ration binaire unique
En combinant les concepts ci-dessus donne une des structures les plus importantes en math??matiques: un groupe . Un groupe est une combinaison d'un ensemble S et un seul op??ration binaire '*', d??fini en aucune fa??on que vous choisissez, mais avec les propri??t??s suivantes:
- Un ??l??ment de l'identit?? e existe, de sorte que pour chaque membre a de S, e * A et A * e sont ?? la fois identique ?? un.
- Chaque ??l??ment a un inverse: pour chaque membre d'un de S, il existe un ??l??ment -1 de telle sorte que a * a -1 et -1 * a sont toutes deux identiques ?? l'??l??ment d'identit??.
- L'op??ration est associative: si a, b et c sont des membres de S, alors (a * b) * c est identique ?? a * (b * c).
Si un groupe est ??galement commutative - ce est, pour les deux membres A et B de S, a * b est identique ?? B * A - puis le groupe est dit ??tre Ab??lien.
Par exemple, l'ensemble des entiers sous l'op??ration d'addition est un groupe. Dans ce groupe, l'??l??ment d'identit?? est ??gal ?? 0 et l'inverse de tout ??l??ment est un son n??gation, - a. L'exigence d'associativit?? est atteint, parce que, pour des entiers a, b et c, (a + b) + c = a + (b + c)
Les non nuls nombres rationnels forment un groupe pour la multiplication. Ici, l'??l??ment d'identit?? est ??gal ?? 1, ??tant donn?? que 1 ?? a = a = a ?? 1 pour tout nombre rationnel a. L'inverse d'une est une / a, depuis une ?? 1 / a = 1.
Les entiers sous l'op??ration de multiplication, cependant, ne forment pas un groupe. Ce est parce que, en g??n??ral, l'inverse multiplicatif d'un nombre entier ne est pas un nombre entier. Par exemple, la figure 4 est un nombre entier, mais son inverse multiplicatif est de 1/4, ce qui ne est pas un nombre entier.
La th??orie des groupes est ??tudi?? dans la th??orie des groupes . Un r??sultat majeur de cette th??orie est la classification des groupes simples finis, principalement publi??s entre environ 1955 et 1983, qui est pens?? pour classer tous les fini groupes simples dans environ 30 types de base.
| Exemples | ||||||||||
| Set: | Nombres naturels  | Entiers 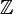 | Nombres rationnels 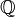 (Aussi r??el (Aussi r??el  et complexe et complexe 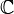 num??ros) num??ros) | Entiers mod 3: {0,1,2} | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Op??ration | + | X (w / o z??ro) | + | X (w / o z??ro) | + | - | X (w / o z??ro) | ?? (w / o z??ro) | + | X (w / o z??ro) |
| Ferm?? | Oui | Oui | Oui | Oui | Oui | Oui | Oui | Oui | Oui | Oui |
| Identit?? | 0 | 1 | 0 | 1 | 0 | N / A | 1 | N / A | 0 | 1 |
| Inverse | N / A | N / A | -a | N / A | -a | N / A | 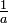 | N / A | 0,2,1, respectivement | NA, 1, 2, respectivement |
| Associatif | Oui | Oui | Oui | Oui | Oui | Aucun | Oui | Aucun | Oui | Oui |
| Commutative | Oui | Oui | Oui | Oui | Oui | Aucun | Oui | Aucun | Oui | Oui |
| Structure | monoid | monoid | Groupe ab??lien | monoid | Groupe ab??lien | quasigroupe | Groupe ab??lien | quasigroupe | Groupe ab??lien | Groupe ab??lien (  ) ) |
Semigroups, quasigroupes, et mono??des sont des structures semblables ?? des groupes, mais plus g??n??rale. Elles comprennent un ensemble et une op??ration binaire ferm??, mais ne satisfont pas n??cessairement les autres conditions. Un semigroupe a une op??ration binaire associative, mais pourrait ne pas avoir un ??l??ment d'identit??. Un mono??de est un semi-groupe qui ne avoir une identit??, mais pourraient ne pas avoir un inverse pour chaque ??l??ment. Un quasigroupe satisfait une exigence que tout ??l??ment peut ??tre transform?? en un autre par une pr?? uniques ou post-op??ratoire; Cependant l'op??ration binaire pourrait ne pas ??tre associative. Tous sont par exemple de groupo??des, les structures avec une op??ration binaire sur lequel aucune autre condition ne est impos??e.
Tous les groupes sont mono??des, et tous les mono??des sont semigroupes.
Anneaux et les champs-structures d'un ensemble avec deux op??rations binaires particuli??res, (+) et (x)
Les groupes ont une seule op??ration binaire. Afin d'expliquer le comportement des diff??rents types de num??ros, structures avec deux op??rateurs doivent ??tre ??tudi??es. La plus importante d'entre elles sont anneaux, et domaines.
Distributivity g??n??raliser la loi distributive pour les nombres, et pr??cise l'ordre dans lequel les op??rateurs devraient ??tre appliqu??es, (appel?? priorit??). Pour les entiers (a + b) x c = a + b ?? c ?? c et c ?? (a + b) = c ?? a + b ?? c et x est dite distributive plus +.
Un anneau a deux op??rations binaires (+) et (x), avec distributive ?? plus +. Sous le premier op??rateur (+) il forme un groupe ab??lien. Dans le cadre du deuxi??me op??rateur (x) il est associative, mais il n'a pas besoin d'avoir une identit??, ou ?? l'inverse, de sorte que la division ne est pas autoris??. L'??l??ment d'identit?? additive (+) se ??crit 0 et l'inverse additif d'un se ??crit - a.
Les entiers sont un exemple d'un anneau. Les entiers ont des propri??t??s suppl??mentaires qui en font un int??gre.
Un champ est un anneau avec la propri??t?? suppl??mentaire que tous les ??l??ments excluant 0 forment un groupe ab??lien sous ??. Le (x) l'identit?? multiplicatif est ??crit comme une et l'inverse multiplicatif d'un est ??crit comme un -1.
Les nombres rationnels, les nombres r??els et les nombres complexes sont tous des exemples de domaines.
Objets appel??s alg??bres
Le mot alg??bre est ??galement utilis?? pour diverses structures alg??briques :
- Alg??bre sur un corps ou plus g??n??ralement Alg??bre sur un anneau
- Alg??bre sur un ensemble
- Alg??bre de Boole
- F-alg??bre et F-cog??bre dans th??orie des cat??gories
- Tribu
Histoire

Les origines de l'alg??bre peuvent ??tre attribu??s ?? l'ancienne Babyloniens, qui ont d??velopp?? une avanc??e syst??me arithm??tique avec laquelle ils ont pu faire des calculs de fa??on alg??brique. Avec l'utilisation de ce syst??me, ils ont ??t?? en mesure d'appliquer des formules et calculer des solutions pour les valeurs inconnues pour une classe de probl??mes g??n??ralement r??solus aujourd'hui en utilisant des ??quations lin??aires , ??quations du second degr?? , et ??quations lin??aires pour une p??riode ind??termin??e. En revanche, la plupart Egyptiens de cette ??poque, et la plupart des Indiens , Grec et Math??maticiens chinois dans le premier mill??naire avant JC, habituellement r??solu ces ??quations par g??om??triques m??thodes, telles que celles d??crites dans le Papyrus Math??matique Rhind, Sulba soutras, ??l??ments d'Euclide , et Les Neuf Chapitres sur l'art math??matique. Le travail g??om??trique des Grecs, typ?? dans les ??l??ments, ?? condition que le cadre de la g??n??ralisation des formules-del?? de la solution de probl??mes particuliers dans des syst??mes plus g??n??raux de ??noncer et r??soudre des ??quations.
Plus tard, les math??maticiens indiens ont d??velopp?? des m??thodes alg??briques ?? un haut degr?? de sophistication. Bien que Diophante et les Babyloniens utilis??s principalement m??thodes ad hoc sp??ciaux pour r??soudre des ??quations, Brahmagupta fut le premier ?? r??soudre des ??quations en utilisant des m??thodes g??n??rales. Il a r??solu les ??quations ind??termin??es lin??aires, ??quations du second degr??, du second ordre ??quations ind??termin??es et ??quations ?? variables multiples.
Le mot ??alg??bre?? est nomm?? d'apr??s l' arabe mot "al-Jabr" dans le titre du livre al-Kitab al-muḫtaṣar f?? al-hisab Gabr wa-l-muqabala, ce qui signifie Le livre de synth??se concernant Calcul par transposition et la r??duction, un livre ??crit par le Math??maticien perse Al-Khwarismi en 820. Le mot Al-Jabr signifie ??r??union??. Le math??maticien hell??nistique Diophante a toujours ??t?? connu comme ??le p??re de l'alg??bre" mais le d??bat existe maintenant de savoir si ou non Al-Khwarizmi devrait prendre ce titre. Ceux qui soutiennent le point Al-Khwarizmi au fait qu'une grande partie de son travail sur la r??duction est encore en usage aujourd'hui et qu'il a donn?? une explication exhaustive de r??soudre des ??quations du second degr??. Ceux qui soutiennent Soulignent le fait que l'alg??bre trouv?? dans Al-Jabr est plus ??l??mentaire que l'alg??bre trouv?? dans Arithmetica et que Arithmetica Diophante est syncop?? tandis Al-Jabr est enti??rement rh??torique. Un autre math??maticien perse, Omar Khayyam, d??velopp?? la g??om??trie alg??brique et a trouv?? la solution g??om??trique g??n??rale de la ??quation cubique. Les math??maticiens indiens Mahavira et Bhaskara II, et le math??maticien chinois Zhu Shijie, a r??solu plusieurs cas de cube, quartique, quintique et d'ordre sup??rieur polyn??mes ??quations.
Un autre ??v??nement cl?? dans le d??veloppement de l'alg??bre est la solution alg??brique g??n??rale des ??quations cubiques et quartiques, d??velopp?? dans le milieu du 16??me si??cle. L'id??e d'un facteur d??terminant a ??t?? d??velopp?? par Math??maticien japonais Kowa Seki au 17??me si??cle, suivie par Gottfried Leibniz dix ans plus tard, dans le but de syst??mes d'??quations lin??aires simultan??es utilisant la r??solution de matrices . Gabriel Cramer a ??galement travaill?? sur des matrices et d??terminants dans le 18??me si??cle. alg??bre abstraite a ??t?? d??velopp?? dans le 19??me si??cle, se concentrant initialement sur ce qu'on appelle aujourd'hui la th??orie de Galois , et probl??mes de constructibilit??.
Les ??tapes du d??veloppement de l'alg??bre symbolique sont ?? peu pr??s comme suit:
- Alg??bre rh??torique, qui a ??t?? d??velopp?? par les Babyloniens et est rest??e dominante jusqu'?? la 16??me si??cle;
- Alg??bre g??om??trique constructive, qui a ??t?? soulign?? par le Math??maticiens grecs classiques indiennes et v??diques;
- Syncop?? alg??bre, tel que d??velopp?? par Diophante, Et la Brahmagupta Bakhshali Manuscrit; et
- Alg??bre symbolique, qui a ??t?? initi??e par Abu al-Hasan ibn Ali al-Qalasadi et voit son point culminant dans le travail de Gottfried Leibniz .

Une chronologie des principaux d??veloppements alg??briques sont comme suit:
- Circa 1800 BC: Le Old babylonienne Strassburg tablette cherche la solution d'une ??quation elliptique quadratique.
- Circa 1600 BC: Le Plimpton 322 tablette donne un tableau de Triplets pythagoriciens dans babylonienne Manuscrit cun??iforme.
- Circa 800 avant JC: math??maticien indien Baudhayana, dans son Baudhayana Sulba Sutra, d??couvre triplets pythagoriciens alg??brique, trouve des solutions g??om??triques d'??quations lin??aires et ??quations du second degr?? de la forme ax 2 = c et ax 2 + bx = c, et trouve deux ensembles de solutions int??grales positifs ?? un ensemble de simultan??e ??quations diophantiennes.
- Circa 600 avant JC: math??maticien indien Apastamba, dans son Apastamba Sulba Sutra, r??sout l'??quation lin??aire g??n??ral et utilise des ??quations diophantiennes simultan??es avec jusqu'?? cinq inconnues.
- Circa 300 avant JC: Dans le livre II de ses ??l??ments, Euclide donne une construction g??om??trique avec des outils euclidiennes pour la solution de l'??quation quadratique pour les racines r??els positifs. La construction est due ?? l'??cole pythagoricienne de la g??om??trie.
- Circa 300 avant JC: Une construction g??om??trique pour la solution du cube est demand??e (doubler le probl??me de cube). Il est maintenant bien connu que le cube g??n??rale n'a pas de telle solution en utilisant des outils euclidiennes .
- Circa 100 avant JC: ??quations alg??briques sont trait??s dans le livre de math??matiques chinoises (Les Neuf Chapitres sur l'art math??matique) de Jiuzhang, qui contient des solutions d'??quations lin??aires r??solus en utilisant la r??gle de la double fausse position, solutions g??om??triques des ??quations du second degr??, et les solutions de matrices ??quivalentes ?? la m??thode moderne, pour r??soudre des syst??mes d'??quations lin??aires simultan??es.
- Circa 100 avant JC: Le Manuscrit Bakhshali ??crit en Inde ancienne utilise une forme de notation alg??brique en utilisant des lettres de l'alphabet et d'autres signes, et contient des ??quations cubiques et quartiques, solutions alg??briques des ??quations lin??aires avec jusqu'?? cinq inconnues, la formule alg??brique g??n??ral pour l'??quation quadratique, et des solutions d'??quations du second degr?? pour une p??riode ind??termin??e et des ??quations simultan??es.
- Circa 150 AD: H??ron d'Alexandrie traite des ??quations alg??briques en trois volumes de math??matiques.
- Circa 200: Diophante, qui a v??cu en Egypte et est souvent consid??r?? comme le ??p??re de l'alg??bre", ??crit son c??l??bre Arithmetica, une oeuvre avec des solutions d'??quations alg??briques et sur la th??orie des nombres.
- 499: math??maticien indien Aryabhata, dans son trait?? Aryabhatiya, obtient des solutions de nombre entier d'??quations lin??aires par une m??thode ??quivalente ?? celle moderne, d??crit la solution int??grale g??n??rale de l'??quation lin??aire ind??termin??e et donne des solutions int??grales d'??quations lin??aires simultan??es pour une p??riode ind??termin??e.
- Circa 625: math??maticien chinois Wang Xiaotong trouve des solutions num??riques des ??quations cubiques.
- 628: math??maticien indien Brahmagupta, dans son trait?? Brahma Sputa Siddhanta, invente la chakravala m??thode de r??soudre des ??quations du second degr?? pour une p??riode ind??termin??e, y compris L'??quation de Pell, et donne des r??gles pour r??soudre des ??quations lin??aires et quadratiques.
- 820: Le mot est d??riv?? de l'alg??bre op??rations d??crites dans le trait?? r??dig?? par le Math??maticien persan Muhammad ibn Musa al-Ḵwārizmī intitul?? Al-Kitab al-Jabr wa-l-Muqabala (qui signifie ??Le Compendious livre sur le calcul par l'ach??vement et ??quilibrage??) sur la solution syst??matique de lin??aire et ??quations du second degr?? . Al-Khwarizmi est souvent consid??r?? comme le ??p??re de l'alg??bre", une grande partie de dont les travaux sur la r??duction a ??t?? inclus dans le livre et ajout?? ?? de nombreuses m??thodes que nous avons maintenant en alg??bre.
- Circa 850: Math??maticien persan al-Mahani con??ut l'id??e de r??duire les probl??mes g??om??triques telles que la duplication du cube pour des probl??mes d'alg??bre.
- Circa 850: math??maticien indien Mahavira r??sout diverses ??quations du second degr??, cubes, quartiques, quintique et d'ordre sup??rieur, ainsi que quadratique ind??termin??e, ??quations cubiques et d'ordre sup??rieur.
- Circa 990: Persan Abu Bakr al-Karaji, dans son trait?? al-Fakhri, d??veloppe davantage l'alg??bre en ??tendant la m??thodologie d'Al-Khwarizmi d'int??grer puissances enti??res et les racines int??grante de quantit??s inconnues. Il remplace op??rations g??om??triques de l'alg??bre avec des op??rations arithm??tiques modernes, et d??finit le mon??mes x, x 2, x 3, ... et 1 / x, 1 / x 2, 1 / x 3, ... et donne des r??gles pour les produits de deux quelconques de ceux-ci.
- Circa 1050: math??maticien chinois Jia Xian trouve des solutions num??riques d'??quations alg??briques.
- 1072: Math??maticien persan Omar Khayyam d??veloppe la g??om??trie alg??brique et, dans le Trait?? sur la d??monstration des probl??mes de l'alg??bre, donne une classification compl??te des ??quations cubiques avec des solutions g??om??triques g??n??rales trouv??s par l'interm??diaire d'intersection sections coniques.
- 1114: math??maticien indien Bhaskara, dans son Bijaganita (alg??bre), reconna??t que un nombre positif a la fois positif et n??gatif racine carr??e , et r??sout divers ??quations polynomiales cubes, quartique et d'ordre sup??rieur, ainsi que l'??quation quadratique ind??termin?? g??n??ral.
- 1202: Alg??bre est introduit dans l'Europe en grande partie gr??ce au travail de Leonardo Fibonacci de Pise dans son travail Liber Abaci.
- Circa 1300: math??maticien chinois Zhu Shijie traite alg??bre de polyn??mes, r??sout les ??quations du second degr??, ??quations simultan??es et ??quations avec jusqu'?? quatre inconnues, et num??riquement r??sout certains quartique, quintique et d'ordre sup??rieur ??quations polynomiales.
- Circa 1400: math??maticien indien Madhava de Sangamagramma trouve m??thodes it??ratives de solution approch??e d'??quations non lin??aires.
- Circa 1450: math??maticien arabe Abu al-Hasan ibn Ali al-Qalasadi pris "les premiers pas vers l'introduction de symbolisme alg??brique. "Il a repr??sent?? symboles math??matiques en utilisant des caract??res de la Alphabet arabe.
- 1535: Nicolo Fontana Tartaglia et d'autres math??maticiens en Italie r??solus ind??pendamment l'??quation cubique g??n??ral.
- 1545: Girolamo Cardano publie Ars magna - Le grand art qui donne la solution de Fontana ?? l'??quation quartique g??n??ral.
- 1572: Rafael Bombelli reconna??t les racines complexes de la cubique et am??liore la notation actuelle.
- 1591: Fran??ois Vi??te d??veloppe une meilleure notation symbolique pour divers pouvoirs d'un inconnu et utilise les voyelles et les consonnes pour inconnues des constantes dans En Artem analyticam isagoge.
- 1631: Thomas Harriot dans une publication posthume utilise la notation exponentielle et est le premier ?? utiliser des symboles pour indiquer ??inf??rieur ???? et ??sup??rieur??.
- 1682: Gottfried Wilhelm Leibniz d??veloppe sa notion de manipulation symbolique des r??gles formelles qu'il appelle characteristica generalis.
- 1680: math??maticien japonais Kowa Seki, dans sa m??thode de r??soudre les probl??mes dissimul??s, d??couvre le facteur d??terminant , et Nombres de Bernoulli.
- 1750: Gabriel Cramer, dans son trait?? Introduction ?? l'analyse des courbes alg??briques, d??clare La r??gle et les ??tudes de Cramer alg??brique des courbes, des matrices et d??terminants.
- 1824: Niels Henrik Abel se est av??r?? que l'??quation quintique g??n??rale est insoluble par les radicaux.
- 1832: la th??orie de Galois est d??velopp?? par Evariste Galois dans son travail sur l'alg??bre abstraite.

