Groupe cyclique

Dans la th??orie des groupes , un groupe cyclique ou un groupe monog??ne est un groupe qui peut ??tre g??n??r??e par un ??l??ment unique, en ce sens que le groupe comporte un ??l??ment g (appel?? " g??n??rateur "du groupe) de telle sorte que, lors de l'??criture par multiplication, chaque ??l??ment du groupe est une puissance de g (un multiple de g lorsque la notation est additif).

D??finition

Un groupe cyclique G est appel?? se il existe un ??l??ment g de G tel que G = <g> g = ^{n | ⁿ est un nombre entier}. Depuis ne importe quel groupe g??n??r??e par un ??l??ment dans un groupe est un sous-groupe de ce groupe, montrant que la seule sous-groupe de G de groupe qui contient g G est elle-m??me suffit ?? montrer que G est cyclique.

Par exemple, si G = {g ^0, g ^1, g ^2, g ^3, g ^4, g ^5} est un groupe, puis ⁶ g = g ^0, et G est cyclique. En fait, G est essentiellement la m??me que (ce est- isomorphe ??) l'ensemble {0, 1, 2, 3, 4, 5} avec addition modulo 6. Par exemple, 1 + 2 = 3 (mod 6) correspond ?? ¹ g ² g ?? g = ^3, et 2 + 5 = 1 (mod 6) correspond ?? ² g ?? g ⁵ = g = g ^{1 7,} et ainsi de suite . On peut utiliser l'isomorphisme φ d??finie par φ (g ⁱ⁾ = i.

Pour tout entier positif n il ya exactement un groupe cyclique (?? isomorphisme pr??s) dont l'ordre est n, et il ya exactement un groupe cyclique infini (les entiers de moins de plus). Ainsi, les groupes cycliques sont les groupes les plus simples et ils sont totalement class??s.

Le nom ??cyclique?? peut ??tre trompeuse: il est possible de g??n??rer un nombre infini d'??l??ments et non former des cycles litt??rales; ce est, tous les 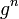est distincte. (On peut dire qu'il a une infiniment long cycle.) Un groupe g??n??r?? de cette mani??re est appel?? un groupe cyclique infini, et est isomorphe au groupe additif des nombres entiers Z.

??tant donn?? que les groupes cycliques sont ab??lien, ils sont souvent ??crits additive et not??s Z _n. Toutefois, cette notation peut ??tre probl??matique pour les th??oriciens des nombres , car il entre en conflit avec la notation habituelle pour p nombre -adique anneaux ou localisation ?? un id??al premier. Le notations quotient Z / n Z, Z / n, et Z / (n) sont des solutions standard. Nous adoptons la premi??re de ces ici pour ??viter la collision de la notation. Voir aussi la section sous-groupes et la notation ci-dessous.

On peut ??crire le groupe multiplicativement, et notons par C _n, o?? n est l'ordre (qui peut ??tre ∞). Par exemple, g ³ g ⁴ g = ² ?? C _5, alors que 3 + 4 = 2 dans Z / Z 5.

Propri??t??s

Le th??or??me fondamental de groupes cycliques stipule que si G est un groupe cyclique d'ordre n puis tous sous-groupe de G est cyclique. En outre, l'ordonnance d'un sous-groupe de G est un diviseur de n et pour chaque diviseur positif k de n le groupe G a exactement un sous-groupe d'ordre k. Cette propri??t?? caract??rise groupes cycliques finis: un groupe d'ordre n est cyclique si et seulement si pour tout diviseur d de n le groupe poss??de au plus un sous-groupe d'ordre d. Parfois, la d??claration ??quivalente est utilis??e: un groupe d'ordre n est cyclique si et seulement si pour tout diviseur d de n le groupe a exactement un sous-groupe d'ordre d.

Chaque groupe cyclique fini est isomorphe au groupe {[0], [1], ..., [n - 1]} des entiers modulo n, par addition, et tout groupe cyclique infini est isomorphe ?? Z (l'ensemble de tous les entiers) sous addition. Ainsi, il suffit de regarder ces groupes ?? comprendre les propri??t??s de groupes cycliques en g??n??ral. Ainsi, des groupes cycliques sont l'un des groupes les plus simples ?? ??tudier et ?? un certain nombre de propri??t??s int??ressantes sont connus.

??tant donn?? un groupe cyclique G d'ordre n (n peut ??tre infini) et pour tout g dans G,

• G est ab??lien; ce est, leur op??ration de groupe est commutatif: gh = hg (pour tout h dans G). Il en est ainsi depuis g + h mod n = h + g mod n.
• Si n est fini, alors g = g ^{n 0} est un ??l??ment du groupe de l'identit??, puisque n = 0 mod n.
• Si n = ∞, alors il ya exactement deux g??n??rateurs: ?? savoir 1 et -1 pour Z, et tous les autres mapp??s ?? eux sous un isomorphisme dans d'autres groupes cycliques infinis.
• Si n est fini, alors il ya exactement φ (n) g??n??rateurs o?? φ est le Fonction de phi d'Euler
• Chaque sous-groupe de G est cyclique. En effet, chaque sous-groupe fini de G est un groupe de {0, 1, 2, 3, ..., m - 1} avec addition modulo m. Et chaque sous-groupe infini de G est m Z pour un m, qui est bijective ?? (donc isomorphe ??) Z.
• G _n est isomorphe ?? Z / n Z ( groupe de facteurs de Z sur Z n) depuis Z / n Z = {0 + Z n, Z n + 1, n + 2 Z, Z n + 3, 4 + Z n, ..., n - 1 + n Z } 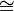{0, 1, 2, 3, 4, ..., n - 1} pour l'addition modulo n.

Plus g??n??ralement, si d est un diviseur de n, alors le nombre d'??l??ments dans Z / n qui ont ordre d est φ (d). L'ordre de la classe de r??sidus de m est n / pgcd (n, m).

Si p est un nombre premier , alors le seul groupe ( jusqu'?? isomorphisme) ?? p ??l??ments est le groupe cyclique C ou Z _p / p Z.

Le produit direct de deux groupes cycliques Z / n Z et Z / Z m est cyclique si et seulement si n et m sont premiers entre eux. Ainsi par exemple, Z / Z 12 est le produit direct de Z / Z et Z 3 / Z 4, mais pas le produit direct de Z / 6 Z et Z / Z 2.

La d??finition implique imm??diatement que les groupes cycliques ont tr??s simple pr??sentation du groupe C = _∞ <x |> et C _n = <x | x ^n> pour n fini.

Un groupe cyclique primaire est un groupe de la forme Z / p ^k o?? p est un nombre premier . Le th??or??me fondamental de groupes ab??liens stipule que chaque groupe ab??lien de type fini est le produit direct d'un nombre fini groupes cycliques cycliques et infinis primaires finis.

Z / n Z et Z sont ??galement anneaux commutatifs . Si p est premier, alors Z / p Z est un corps fini, ??galement d??sign?? par F _p ou GF (p). Chaque champ ?? p ??l??ments est isomorphe ?? celui-ci.

Le unit??s de l'anneau Z / n Z sont les num??ros premier avec n. Ils forment un groupe sous la multiplication modulo n avec φ (n) ??l??ments (voir ci-dessus). Il est ??crit que (Z / n Z) ^??. Par exemple, nous obtenons (Z / n Z) ^?? = {1,5} lorsque n = 6, et obtenir des (Z / n Z) ^?? = {1,3,5,7} lorsque n = 8.

En fait, on sait que (Z / Z n) ^?? est cyclique si et seulement si n est ??gal ?? 2 ou 4 ou 2 ou p ^k p ^k pour un impaire nombre premier p et k ≥ 1, dans ce cas, tous les g??n??rateurs de (Z / n Z) ^?? est appel?? primitive modulo n racine. Ainsi, (Z / Z n) ^?? est cyclique pour n = 6, mais pas pour n = 8, o?? il est isomorphe ?? la place Groupe de Klein.

Le groupe (Z / p Z) ^?? est cyclique avec p - 1 ??l??ments pour chaque nombre premier p, et est aussi ??crit (Z / p Z) ^* parce qu'il se compose des ??l??ments non nuls. Plus g??n??ralement, tous les finis sous-groupe du groupe multiplicatif de toute champ est cyclique.

Exemples

En 2D et 3D de la groupe de sym??trie pour n -fois sym??trie de rotation est C _n, d'un groupe type abstrait Z _n. En 3D, il ya ??galement d'autres groupes de sym??trie qui sont alg??briquement m??me, voir Groupes de sym??trie cyclique en 3D.

Notez que le groupe S ¹ de toutes les rotations d'un cercle (le Groupe de cercle) ne est pas cyclique, car il ne est m??me pas d??nombrable.

La ^n-i??me racines de l'unit?? forment un groupe cyclique d'ordre n pour la multiplication. par exemple, 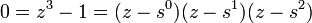o?? 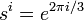et un groupe de la multiplication est cyclique.

Le De chaque groupe de Galois fini l'extension du champ d'un champ fini est fini et cyclique; ?? l'inverse, ??tant donn?? un corps fini F et un groupe cyclique fini G, il est une extension finie de F dont le groupe de Galois G est sur le terrain.

Repr??sentation

Le graphiques du cycle de groupes cycliques finis sont tous les polygones n -sided avec les ??l??ments aux sommets. Le sommet sombre dans les graphiques ci-dessous de cycle pour tenir l'??l??ment d'identit?? et les autres sommets sont les autres ??l??ments du groupe. Un cycle est constitu?? de puissances successives de l'un des ??l??ments connect??s ?? l'??l??ment d'identit??.

C 1	C 2	C 3	C 4	C 5	C 6	C 7	C 8

Le la th??orie de la repr??sentation du groupe cyclique est un cas de base essentiel pour la th??orie des repr??sentations des groupes finis plus g??n??rales. Dans le affaire complexe, une repr??sentation d'un groupe cyclique se d??compose en une somme directe de caract??res lin??aires, faisant le lien entre la th??orie des caract??res et la th??orie de la repr??sentation transparente. Dans le cas caract??ristique positive, les repr??sentations ind??composables du groupe cyclique former un mod??le et une base inductive pour la th??orie de la repr??sentation des groupes avec cyclique Sous-groupes de Sylow et plus g??n??ralement la th??orie de la repr??sentation des blocs de d??faut cyclique.

Sous-groupes et la notation

Tous et des sous-groupes groupes quotients de groupes cycliques sont cycliques. Plus pr??cis??ment, tous les sous-groupes de Z sont de la forme m Z, avec un nombre entier m ≥0. Tous ces sous-groupes sont diff??rents, et ?? part le groupe trivial (pour m = 0) sont tous isomorphe ?? Z. Le r??seau de sous-groupes de Z est isomorphe au double du r??seau des nombres naturels ordonn??es par la divisibilit?? . Tous les groupes de facteurs de Z sont limit??es, sauf pour l'exception trivial Z / {0} = Z / 0 Z. Pour chaque diviseur D positif de n, le groupe quotient Z / Z n a une pr??cision sous-groupe d'ordre d, l'une g??n??r??e par la classe de r??sidus de n / d. Il n'y a pas d'autres sous-groupes. Le r??seau de sous-groupes est donc isomorphe ?? l'ensemble des diviseurs de n, ordonn??e par la divisibilit??. En particulier, un groupe cyclique est simple si et seulement si son ordre (le nombre de ses ??l??ments) est premier.

Utilisation du groupe quotient formalisme, Z / n Z est une notation standard pour le groupe cyclique additif ?? n ??l??ments. En terminologie annulaire, le sous-groupe Z n est la id??al (n), de sorte que le quotient peut ??galement ??tre ??crit Z / (n) ou Z / n sans abus de notation. Ces solutions de rechange ne sont pas incompatibles avec la notation pour les p entiers -adiques. La derni??re forme pr??sente l'avantage suppl??mentaire qu'il lit de la m??me fa??on que le groupe ou l'anneau est souvent d??crit verbalement, ??Zee mod en".

Comme un probl??me pratique, on peut ??tre donn?? un sous-groupe fini d'ordre n C, g??n??r??e par un ??l??ment g, et a demand?? de trouver la taille m du sous-groupe engendr?? par G ^k pour un certain entier k. Ici m sera le plus petit entier> 0 tel que mk est divisible par n. Il est donc n / m o?? m = (k, n) est la pgcd de k et n. En d'autres termes, la indice du sous-groupe engendr?? par g ^k est m. Ce raisonnement est connu comme le algorithme de calcul de l'indice, dans la th??orie des nombres .

Endomorphismes

Le anneau commutatif endomorphisme du groupe Z / n Z est isomorphe ?? Z / n Z lui-m??me en tant que anneau. Sous cet isomorphisme, le nombre r correspond ?? la endomorphisme de Z / n Z qui mappe chaque ??l??ment ?? la somme de r copies de celui-ci. Ce est une bijection si et seulement si r est premier avec n, de sorte que le groupe automorphisme de Z / n Z est isomorphe au groupe de base (Z / n Z) ^?? (voir ci-dessus).

De m??me, l'anneau des endomorphismes du groupe additif Z est isomorphe ?? l'anneau Z. Son groupe d'automorphismes est isomorphe au groupe d'unit??s de l'anneau Z, ce est-?? {-1, 1} 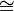C _2.

Pratiquement groupes cycliques

Un groupe est appel?? pratiquement cyclique si elle contient un sous-groupe cyclique fini de index. Il est connu qu'un type fini groupe discret avec exactement deux extr??mit??s est pratiquement cyclique. Chaque sous-groupe ab??lien d'un Groupe hyperbolique Gromov est pratiquement cyclique.