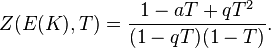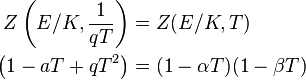Courbe elliptique
Renseignements g??n??raux
SOS Enfants, qui se d??roule pr??s de 200 sos ??coles dans le monde en d??veloppement, a organis?? cette s??lection. Cliquez ici pour en savoir plus sur le parrainage d'enfants.

En math??matiques , une courbe elliptique est une lisse, projective courbe alg??brique genre une, sur laquelle il ya un point O sp??cifi??. Une courbe elliptique est en fait un vari??t?? ab??lienne - autrement dit, il a une multiplication d??fini alg??briquement, par rapport ?? laquelle il est (n??cessairement commutatif ) groupe - O et sert d'??l??ment d'identit??. Souvent, la courbe elle-m??me, sans O sp??cifi??, est appel?? une courbe elliptique.
Toute courbe elliptique peut ??tre ??crit comme une courbe alg??brique plane d??finie par une ??quation de la forme:
qui est non singuli??re; ce est son graphe n'a pas cuspides ou auto-intersections. (Quand le caract??ristique du champ de coefficient est ??gal ?? 2 ou 3, l'??quation ci-dessus ne est pas tout ?? fait assez g??n??ral pour comprendre tous non singuli??re courbes cubes; voir ci-dessous pour une d??finition plus pr??cise.) Le point O est en fait le " point ?? l'infini "dans le plan projectif.
Si y 2 = P (x), o?? P est un polyn??me quelconque de degr?? trois pouces x r??p??t??es sans racines, on obtient alors une courbe plane non singuli??re de une genre, qui est donc ??galement une courbe elliptique. Si P est de degr?? quatre et est quadratfrei cette ??quation d??crit ?? nouveau une courbe plane d'une genre; cependant, il n'a pas le choix naturel de l'??l??ment d'identit??. Plus g??n??ralement, toute courbe alg??brique du genre ci, par exemple ?? partir de l'intersection de deux quadriques int??gr??s dans l'espace tridimensionnel projective, est appel??e une courbe elliptique, ?? condition qu'il ait au moins un point rationnel.
En utilisant la th??orie de fonctions elliptiques, il peut ??tre d??montr?? que les courbes elliptiques d??finies sur les nombres complexes correspondent ?? plongements du tore dans le plan projectif complexe. Le tore est ??galement un groupe ab??lien, et en fait, ce est ??galement une correspondance groupe isomorphisme.
Les courbes elliptiques sont particuli??rement importants dans la th??orie des nombres , et constituent un domaine majeur de la recherche actuelle; par exemple, ils ont ??t?? utilis??s dans la preuve, par Andrew Wiles (assist?? par Richard Taylor), du dernier th??or??me de Fermat . Ils trouvent ??galement des applications dans la cryptographie (voir l'article cryptographie ?? courbe elliptique) et factorisation entier.
Une courbe elliptique ne est pas une ellipse : voir int??grale elliptique de l'origine du terme. Topologiquement, une courbe elliptique est un tore .
Courbes elliptiques sur les nombres r??els
Bien que la d??finition formelle d'une courbe elliptique est assez technique et n??cessite une certaine exp??rience de la g??om??trie alg??brique, il est possible de d??crire quelques caract??ristiques de courbes elliptiques sur les nombres r??els en utilisant uniquement l'??cole secondaire l'alg??bre et la g??om??trie .
Dans ce contexte, une courbe elliptique est une courbe plane d??finie par une ??quation de la forme
o?? a et b sont des nombres r??els. Ce type d'??quation se appelle une ??quation de Weierstrass.
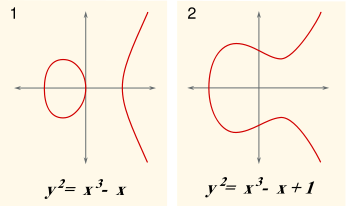
La d??finition de la courbe elliptique exige ??galement que la courbe soit non singuli??re. G??om??triquement, cela signifie que le graphe ne est pas cuspides, auto-intersections ou points isol??s. Alg??briquement, il se agit de calculer la discriminant
La courbe est non singuli??re si et seulement si le discriminant ne est pas ??gale ?? z??ro. (Bien que le facteur ne semble pas pertinent ici -16, il se av??re ??tre pratique dans une ??tude plus pouss??e des courbes elliptiques.)
La (vraie) graphique d'une courbe non singuli??re a deux composantes si son discriminant est positif, et un composant se il est n??gatif. Par exemple, dans les graphiques pr??sent??s dans la figure ?? droite, le discriminant dans le premier cas est de 64, et dans le second cas est -368.
La loi de groupe
En ajoutant un "point ?? l'infini", on obtient la version projective de cette courbe. Si P et Q sont deux points de la courbe, on peut d??crire de mani??re unique un troisi??me point qui est l'intersection de la courbe avec la ligne par P et Q. Si la ligne est tangente ?? la courbe en un point, alors ce point est compt?? deux fois; et si la ligne est parall??le ?? l'axe des y, nous d??finissons le troisi??me point que le point "?? l'infini". Exactement une des conditions suivantes est vraie alors pour ne importe quelle paire de points d'une courbe elliptique.
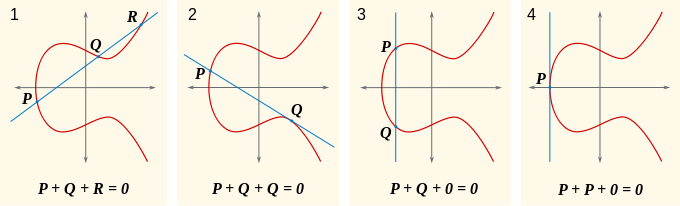
Il est alors possible d'introduire une op??ration de groupe , +, sur la courbe avec les propri??t??s suivantes: on consid??re le point ?? l'infini ?? 0, l'identit?? de groupe; et si une ligne droite coupe la courbe aux points P, Q et R, nous exigeons que P + Q + R = 0 dans le groupe. On peut v??rifier que cela se transforme la courbe dans un groupe ab??lien, et donc dans un vari??t?? ab??lienne. On peut montrer que l'ensemble des K - points rationnels (y compris le point ?? l'infini) forme un sous-groupe de ce groupe. Si la courbe est repr??sent??e par E, puis ce sous-groupe est souvent ??crit sous la forme E (K).
Le groupe ci-dessus peut ??tre d??crit alg??briquement ainsi que g??om??triquement. Compte tenu de la courbe y = 2 x 3 - px - q sur le champ K (dont les caract??ristique que nous supposons ??tre ni deux, ni trois), et les points P = (x P, y P) et Q = (x Q, y Q) sur la courbe, supposent d'abord que x P x Q ≠. Soit s la pente de la ligne contenant P et Q; ce est ?? dire, s = (y P - y Q) / (x P - x Q). Depuis K est un champ, s est bien d??fini. Ensuite, nous pouvons d??finir R = P + Q = (R x, -y R) par
Si x P x = Q (troisi??me et quatri??me volets ci-dessus), puis il ya deux options: si y = P - y Q, y compris le cas o?? y = y P Q = 0, alors la somme est d??finie comme 0; Ainsi, l'inverse de chaque point de la courbe se trouve en r??fl??chissant ?? travers la axe des x. Si y P y = Q ≠ 0 (deuxi??me volet), alors R = P + P = 2 P = (x R, Y R) est donn??e par
Courbes elliptiques sur les nombres complexes
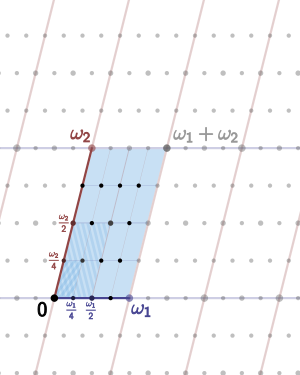
La formulation de courbes elliptiques comme l'incorporation d'un tore dans la plan projectif complexe d??coule naturellement un bien curieux Fonction elliptique de Weierstrass. Ces fonctions et leur d??riv??e premi??re sont li??s par la formule
Ici, G 2 et G 3 sont des constantes; 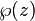 est la fonction elliptique de Weierstrass et
est la fonction elliptique de Weierstrass et 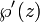 son d??riv??. Il devrait ??tre clair que cette relation est sous la forme d'une courbe elliptique (sur les nombres complexes ). Les fonctions de Weierstrass sont doublement p??riodique; autrement dit, ils sont p??riodiques par rapport ?? une treillis Λ; en substance, les fonctions de Weierstrass sont naturellement d??finis sur un tore T = C / Λ. Ce tore peut ??tre incorpor??e dans le plan projectif complexe au moyen de la carte
son d??riv??. Il devrait ??tre clair que cette relation est sous la forme d'une courbe elliptique (sur les nombres complexes ). Les fonctions de Weierstrass sont doublement p??riodique; autrement dit, ils sont p??riodiques par rapport ?? une treillis Λ; en substance, les fonctions de Weierstrass sont naturellement d??finis sur un tore T = C / Λ. Ce tore peut ??tre incorpor??e dans le plan projectif complexe au moyen de la carte
Cette carte est une groupe isomorphisme, portant la structure de groupe naturel du tore dans le plan projectif. Ce est aussi un isomorphisme de surfaces de Riemann , donc topologiquement, une courbe elliptique donn??e ressemble ?? un tore. Si le treillis Λ est li?? de par multiplication par un nombre non nul ?? un complexe c treillis Λ c, alors les courbes correspondantes sont isomorphes. classes d'isomorphisme de courbes elliptiques sont sp??cifi??s par le j-invariant.
Les classes d'isomorphisme peuvent ??tre comprises d'une mani??re plus simple ainsi. Les constantes g 2 et g 3, appel?? le invariants modulaires, sont d??termin??s de fa??on unique par le r??seau, qui est, par la structure du tore. Cependant, les nombres complexes de la forme champ de fractionnement pour les polyn??mes ?? coefficients r??els, et ainsi de la courbe elliptique peut se ??crire
On constate que
et
de sorte que le discriminant modulaire est
Ici, λ est parfois appel?? le fonction lambda modulaire.
Notez que le uniformisation th??or??me implique que chaque compacte surface de Riemann de genre peut ??tre repr??sent?? comme un tore.
Cela permet ??galement une compr??hension facile du points de torsion sur une courbe elliptique: si le treillis Λ est engendr?? par les p??riodes fondamentales ω 1 et ω 2, puis les n -torsion points sont les (classes d'??quivalence de) points de la forme 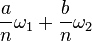 , Pour a et b des nombres entiers dans la gamme de 0 ?? n -1.
, Pour a et b des nombres entiers dans la gamme de 0 ?? n -1.
Sur les nombres complexes, chaque courbe elliptique a neuf les points d'inflexion. Chaque ligne ?? travers deux de ces points passe aussi par un troisi??me point d'inflexion; les neuf points et 12 lignes form??es de cette mani??re forment une r??alisation de la Configuration Hesse.
Courbes elliptiques sur les nombres rationnels
Une courbe E d??finie sur le corps des nombres rationnels est ??galement d??fini sur le corps des nombres r??els, donc la loi d'addition (de points avec coordonn??es r??elles) par la m??thode de la tangente et s??cant peut ??tre appliqu?? ?? E. Les formules explicites montrer que la somme de deux points P et Q avec coordonn??es rationnelles a pour coordonn??es nouveau rationnels, depuis la ligne joignant P et Q a coefficients rationnels. De cette fa??on, on montre que l'ensemble des points rationnels de E forme un sous-groupe du groupe de points r??els de E. Comme ce groupe, ce est un groupe ab??lien, ce est-?? P + Q = Q + P.
La structure de points rationnels
Le r??sultat le plus important est que tous les points peuvent ??tre construits par la m??thode des tangentes et s??cantes ?? partir d'un nombre fini de points. Plus pr??cis??ment la Th??or??me de Mordell-Weil affirme que le groupe E (Q) est un fini g??n??r?? groupe (commutatif). Par le th??or??me fondamental de groupes ab??liens de type fini, il est donc une somme directe finie de copies de Z et des groupes cycliques finis.
La preuve de ce th??or??me repose sur deux ingr??dients: d'abord, on montre que pour tout entier m> 1, le groupe quotient E (Q) / ME (Q) est fini (faible th??or??me de Mordell-Weil). D'autre part, l'introduction d'un fonction de la hauteur h sur les points rationnelle E (Q) d??fini par h (P 0) = 0 et h (P) = log max (| p |, | q |) si P (in??gal au point ?? l'infini P 0) a en abscisse le nombre rationnel x = p / q (avec p et q premiers entre eux). Cette fonction de la hauteur h a la propri??t?? que h (MP) se d??veloppe ?? peu pr??s comme le carr?? de m. En outre, seulement un nombre fini de points rationnels avec hauteur inf??rieure ?? toute existent constante sur E.
La d??monstration du th??or??me est donc une variante de la m??thode de descente infinie et se appuie sur l'application r??p??t??e de Divisions euclidiennes sur E: soit P ∈ E (Q) soit un point rationnel sur la courbe, ??crit P comme la somme 2 P 1 + Q 1 o?? Q 1 est un representant fixe de P dans E (Q) / 2 E (Q ), la hauteur de P 1 est d'environ 1/4 de celle de P (plus g??n??ralement, ne importe quel remplacement, par 2 m> 1, et 1/4 de 1 / m 2). Refaire la m??me chose avec P 1, ce est-??-dire P 1 = P 2 + Q 2 2, alors P = 2 P 2 Q 3 + 3, etc. exprime enfin P comme une combinaison lin??aire de points int??grante Q i et des points dont hauteur est limit??e par une constante fixe choisie ?? l'avance: par la faiblesse du th??or??me de Mordell-Weil et la seconde propri??t?? de la fonction de la hauteur P est ainsi exprim?? en combinaison lin??aire int??grante d'un nombre fini de points fixes.
Jusqu'?? pr??sent, le th??or??me ne est pas efficace car il n'y a pas de proc??dure g??n??rale connue pour d??terminer les representants de E (Q) / ME (Q).
Le rang de E (Q), ce est le nombre de copies de Z ?? E (Q) ou, de fa??on ??quivalente, le nombre de points ind??pendants d'ordre infini, est appel?? le rang de E. Le Conjecture de Birch et Swinnerton-Dyer est pr??occup?? par d??terminer le rang. On conjecture qu'il peut ??tre arbitrairement grand, m??me si seuls exemples avec relativement faible rang sont connus. La courbe elliptique avec le plus grand rang exactement connu est
- y 2 + xy = x 3 − 26 175 960 092 705 884 096 311 701 787 701 203 903 556 438 969 515 x + 51 069 381 476 131 486 489 742 177 100 373 772 089 779 103 253 890 567 848 326 .
Il est de rang 18, trouv??e par Noam Elkies en 2006. Les courbes de rang au moins 28 sont connus, mais leur rang ne est pas exactement connue.
En ce qui concerne les groupes constituant la sous-groupe de torsion E (Q), ce qui suit est connu le sous-groupe de torsion de E (Q) est l'un des 15 groupes suivants (un th??or??me en raison de Barry Mazur): Z / N Z pour N = 1, 2, ..., 10, ou 12, ou Z / 2 Z ?? Z / 2 N Z avec N = 1, 2, 3, 4. Exemples pour tous les cas sont connus . En outre, les courbes elliptiques dont Mordell-Weil sur Q groupes ont les m??mes groupes de torsion appartiennent ?? une famille param??tr??e.
La conjecture de Birch et Swinnerton-Dyer
La Conjecture de Birch et Swinnerton-Dyer (BSD) est l'un des probl??mes du mill??naire de la Clay Mathematics Institute. La conjecture se appuie sur des objets d'analyse et de calcul d??finies par la courbe elliptique en question.
Sur le c??t?? analytique, un ingr??dient important est une fonction d'une variable complexe, L, la Hasse-Weil fonction zeta de E sur Q. Cette fonction est une variante de la Fonction z??ta de Riemann et Fonctions L de Dirichlet. Il est d??fini comme une Euler produit, avec un seul facteur pour chaque nombre premier p.
Pour une courbe E sur Q donn??e par une ??quation minimale
?? coefficients entiers de un i, r??duisant les coefficients modulo p d??finit une courbe elliptique sur la champ fini F p (sauf pour un nombre fini de nombres premiers p, o?? la courbe pr??sente une diminution singularit?? et donc ne parvient pas ?? ??tre elliptique, auquel cas E est dit des mauvaise r??duction en p).
La fonction z??ta d'une courbe elliptique sur un corps fini F p est, dans un certain sens, un la fonction de g??n??ration de l'information de l'assemblage du nombre de points de E avec des valeurs dans le fini extensions de terrain de F p, F p n. Il est donn??,
La somme int??rieur de l'exponentielle ressemble le d??veloppement du logarithme et, en fait, la fonction z??ta ainsi d??fini est un fonction rationnelle:
La fonction z??ta de Hasse-Weil de E sur Q est alors d??fini par la collecte de ces informations, pour tous les nombres premiers p. Elle est d??finie par
o?? ε (p) = 1 si E a bonne r??duction en p et 0 sinon (dans ce cas, un P est d??fini diff??remment que ci-dessus).
Ce produit converge pour 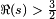 seulement. La conjecture de Hasse affirme que le L admet une -fonction prolongement analytique ?? l'ensemble du plan complexe et satisfait une ??quation fonctionnelle relative, pour tout s, L (E, S) ?? L (E, 2 s). En 1999, ce est r??v??l?? ??tre une cons??quence de la preuve de la conjecture de Shimura-Taniyama-Weil, qui affirme que toute courbe elliptique sur Q est un courbe modulaire, ce qui implique que son -fonction L est la L -fonction d'un forme modulaire dont le prolongement analytique est connue.
seulement. La conjecture de Hasse affirme que le L admet une -fonction prolongement analytique ?? l'ensemble du plan complexe et satisfait une ??quation fonctionnelle relative, pour tout s, L (E, S) ?? L (E, 2 s). En 1999, ce est r??v??l?? ??tre une cons??quence de la preuve de la conjecture de Shimura-Taniyama-Weil, qui affirme que toute courbe elliptique sur Q est un courbe modulaire, ce qui implique que son -fonction L est la L -fonction d'un forme modulaire dont le prolongement analytique est connue.
On peut donc parler des valeurs de L (E, s) ?? ne importe quel nombre complexe s. La conjecture de Birch-Swinnerton-Dyer concerne l'arithm??tique de la courbe pour le comportement de son L -fonction s = 1. Plus pr??cis??ment, il affirme que l'ordre de la L -fonction en s = 1 est ??gal au rang de E et pr??dit la terme principal de la s??rie de Laurent L (E, s) ?? ce point en termes de plusieurs quantit??s attach??s ?? la courbe elliptique.
Tout comme le Hypoth??se de Riemann, cette conjecture a de multiples cons??quences, y compris les deux suivantes:
- Soit n un impair sans carr?? entier. En supposant que la conjecture de Birch et Swinnerton-Dyer, n est la zone d'un triangle rectangle avec des longueurs rationnels secondaires (une nombre congruent) si et seulement si le nombre de triplets de nombres entiers (x, y, z) v??rifiant
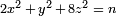 est le double du nombre de triplets satisfaisant
est le double du nombre de triplets satisfaisant 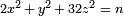 . Cette d??claration, en raison de Tunnell, est li??e au fait que n est un nombre congruent si et seulement si la courbe elliptique
. Cette d??claration, en raison de Tunnell, est li??e au fait que n est un nombre congruent si et seulement si la courbe elliptique 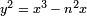 a un point d'ordre infini (donc, en vertu de la conjecture de Birch et Swinnerton-Dyer, son L -fonction a un z??ro ?? 1) rationnelle. L'int??r??t de cette d??claration est que la condition est facilement v??rifi??e.
a un point d'ordre infini (donc, en vertu de la conjecture de Birch et Swinnerton-Dyer, son L -fonction a un z??ro ?? 1) rationnelle. L'int??r??t de cette d??claration est que la condition est facilement v??rifi??e. - Dans une autre direction, certaines m??thodes d'analyse permettent une estimation de l'ordre de z??ro au centre de la bande critique de familles de L -functions. Admettant la conjecture de BSD, ces estimations correspondent ?? l'information sur le rang des familles de courbes elliptiques en question. Par exemple ,: supposons que la hypoth??se de Riemann g??n??ralis??e et la conjecture de BSD, le rang moyen de courbes donn??e par
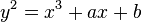 est inf??rieur ?? 2.
est inf??rieur ?? 2.
Le th??or??me de modularit?? et son application ?? le dernier th??or??me de Fermat
Le th??or??me de modularit??, autrefois connue comme la conjecture de Shimura-Taniyama-Weil, affirme que toute courbe elliptique E sur Q est un courbe modulaire, ce est-??-dire, sa fonction z??ta de Hasse-Weil est le L -fonction d'un forme modulaire de poids 2 et de niveau N, o?? N est le conducteur de E (un nombre entier divisible par les m??mes nombres premiers que le discriminant de E, Δ (E).) En d'autres termes, si, par 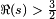 , On ??crit la L -fonction sous la forme
, On ??crit la L -fonction sous la forme
l'expression 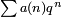 , O?? q = exp (iz 2π) d??finit un modulaire parabolique newform de poids 2 et de niveau N. Pour nombres premiers ℓ pas divisant N, le coefficient
, O?? q = exp (iz 2π) d??finit un modulaire parabolique newform de poids 2 et de niveau N. Pour nombres premiers ℓ pas divisant N, le coefficient 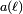 de la forme est ??gal ?? ℓ - le nombre de solutions de l'??quation minimale de la courbe de ℓ modulo.
de la forme est ??gal ?? ℓ - le nombre de solutions de l'??quation minimale de la courbe de ℓ modulo.
Par exemple, pour la courbe elliptique 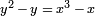 de discriminant (et chef d'orchestre) 37, est associ??e la forme
de discriminant (et chef d'orchestre) 37, est associ??e la forme 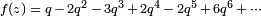 O??
O?? 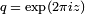 . Pour nombres premiers ℓ distinctes de 37 ans, on peut v??rifier la propri??t?? sur les coefficients. Ainsi, pour ℓ = 3, les solutions de l'??quation modulo 3 sont (0, 0), (0, 1), (2, 0), (1, 0), (1, 1), (2, 1) , au fur et
. Pour nombres premiers ℓ distinctes de 37 ans, on peut v??rifier la propri??t?? sur les coefficients. Ainsi, pour ℓ = 3, les solutions de l'??quation modulo 3 sont (0, 0), (0, 1), (2, 0), (1, 0), (1, 1), (2, 1) , au fur et 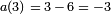 .
.
La conjecture, qui remonte aux ann??es cinquante, a ??t?? compl??tement montr?? en 1999 en utilisant des id??es de Andrew Wiles, qui a d??j?? prouv?? en 1994 pour une grande famille de courbes elliptiques.
Il existe plusieurs formulations de la conjecture. En d??montrant qu'elles sont ??quivalentes est difficile et a ??t?? un sujet principal de la th??orie des nombres dans la seconde moiti?? du 20e si??cle. La modularit?? d'une courbe elliptique E du conducteur N peut ??galement ??tre exprim?? en disant qu'il ya un non constante carte rationnelle d??finie sur Q, de la courbe modulaire 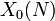 ?? E. En particulier, les points de E peuvent ??tre param??tr??es par fonctions modulaires.
?? E. En particulier, les points de E peuvent ??tre param??tr??es par fonctions modulaires.
Par exemple, une param??trisation modulaire de la courbe 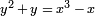 est donn??e par
est donn??e par
o??, comme pr??c??demment, q = exp (iz 2π). Les fonctions x (z) et y (z) sont modulaires de poids 0 et le niveau 37; en d'autres termes ils sont m??romorphe, d??finie sur la demi-plan sup??rieur 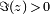 et satisfaire
et satisfaire 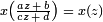 et de m??me pour y (z) pour tout entier a, b, c, d avec ad - bc = 1 et 37 | c.
et de m??me pour y (z) pour tout entier a, b, c, d avec ad - bc = 1 et 37 | c.
Une autre formulation d??pend de la comparaison de repr??sentations de Galois fix??s d'une part ?? courbes elliptiques, et d'autre part ?? des formes modulaires. Cette derni??re formulation a ??t?? utilis??e dans la d??monstration de la conjecture. Traiter avec le niveau des formes (et la connexion au conducteur de la courbe) est particuli??rement d??licate.
L'application la plus spectaculaire de la conjecture est la preuve de th??or??me de Fermat (FLT). Supposons que pour un nombre premier p> 5, l'??quation de Fermat
a une solution avec des entiers non nuls, donc un contre-exemple ?? la FLT. Ensuite, la courbe elliptique
de discriminant 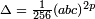 ne peut pas ??tre modulaire. Ainsi, la preuve de la conjecture de Shimura-Taniyama-Weil pour cette famille de courbes elliptiques (appel??es courbes Hellegouarch-Frey) implique la FLT. La preuve du lien entre ces deux d??clarations, bas??e sur une id??e de Gerhard Frey (1985), est difficile et technique. Il a ??t?? cr???? par Kenneth Ribet en 1987.
ne peut pas ??tre modulaire. Ainsi, la preuve de la conjecture de Shimura-Taniyama-Weil pour cette famille de courbes elliptiques (appel??es courbes Hellegouarch-Frey) implique la FLT. La preuve du lien entre ces deux d??clarations, bas??e sur une id??e de Gerhard Frey (1985), est difficile et technique. Il a ??t?? cr???? par Kenneth Ribet en 1987.
Points entiers
Cet article concerne des points P = (x, y) de E tel que x est un nombre entier. Le th??or??me suivant est due ?? CL Siegel: l'ensemble des points P = (x, y) de E (Q) de telle sorte que x est entier est fini. Ce th??or??me peut ??tre g??n??ralis??e ?? points dont les coordonn??es x a un d??nominateur divisible que par un ensemble fini de nombres premiers fixe.
Le th??or??me peut ??tre formul??e de mani??re efficace. Par exemple, si l'??quation de Weierstrass de E coefficients entiers limit??es par une constante H, les coordonn??es (x, y) d'un point de E ?? la fois x et y satisfaire entier:
Par exemple, l'??quation 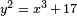 a huit solutions int??grales avec y> 0:
a huit solutions int??grales avec y> 0:
- (X, y) = (1,4), (2,3), (2,5), (4,9), (8,23), (43 282) (52 375), (5 234, 378 661).
Comme autre exemple, L'??quation de Ljunggren, une courbe dont la forme est Weierstrass y 2 = x 3-2 x, n'a que quatre solutions avec y ≥ 0:
- (X, y) = (0,0), (-1,1), (2, 2), (338,6214).
G??n??ralisation aux champs num??riques
Beaucoup des r??sultats pr??c??dents restent valables lorsque le champ de la d??finition de E est un champ de num??ro, ce est-??-dire, un ensemble fini extension de domaine de Q. En particulier, le groupe E (K) de K des points -rationnels d'une courbe elliptique E d??finie sur K est de type fini, qui g??n??ralise le th??or??me de Mordell-Weil-dessus. Un th??or??me de Lo??c Merel montre que pour un nombre entier j donn??, il existe ( ?? isomorphisme pr??s) qu'un nombre fini de groupes qui peuvent se produire que les groupes de torsion de E (K) pour une courbe elliptique d??finie sur un champ de nombre K de degr?? d. Plus pr??cis??ment, il existe un nombre B (d) telle que, pour toute courbe elliptique E d??finie sur un corps de nombres K de degr?? d, un point quelconque de E (K) de torsion est de commander inf??rieur ?? B (d). Le th??or??me est efficace: pour d> 1, si un point de torsion est d'ordre p, avec p premier, alors 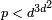 .
.
Quant aux points entiers, le th??or??me de Siegel g??n??ralise ?? la suivante: soit E une courbe elliptique d??finie sur un corps de nombres K, x et y coordonne le Weierstrass. Ensuite, les points de E (K) dont le -Coordonner x est dans la anneau des entiers O K est fini.
Les propri??t??s de la fonction z??ta de Hasse-Weil et la Conjecture de Birch et Swinnerton-Dyer peuvent ??galement ??tre ??tendus ?? cette situation plus g??n??rale.
Courbes elliptiques sur un champ g??n??ral
Les courbes elliptiques peuvent ??tre d??finis sur toute corps K; la d??finition formelle d'une courbe elliptique est une courbe alg??brique projective non singuli??re sur K avec genre 1 avec un point donn?? d??fini sur K.
Si le caract??ristique de K ne est ni deux, ni trois, alors chaque courbe elliptique sur K peut ??tre ??crit sous la forme
o?? p et q sont des ??l??ments de K tel que le droit polyn??me c??t?? x 3 - px - q ne poss??de pas de racines doubles. Si la caract??ristique est 2 ou 3, puis plusieurs termes doivent ??tre conserv??s: en caract??ristique 3, l'??quation la plus g??n??rale l'est de la forme
pour des constantes arbitraires 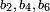 tels que le polyn??me sur le c??t?? droit a des racines distinctes (la notation est choisie pour des raisons historiques). Dans caract??ristique 2, m??me autant ne est pas possible, et l'??quation la plus g??n??rale l'est
tels que le polyn??me sur le c??t?? droit a des racines distinctes (la notation est choisie pour des raisons historiques). Dans caract??ristique 2, m??me autant ne est pas possible, et l'??quation la plus g??n??rale l'est
?? condition que la vari??t?? qu'elle d??finit est non singuli??re. Si caract??ristique ne ??tait pas un obstacle, chaque ??quation se r??duit ?? la pr??c??dente par une modification appropri??e de variables.
On prend g??n??ralement la courbe comme ??tant l'ensemble de tous les points (x, y) qui satisfont ?? l'??quation ci-dessus et de telle sorte que x et y sont des ??l??ments de la cl??ture alg??brique de K. Points de la courbe dont coordonne deux appartiennent ?? K sont appel??s les points K -rationnels.
Isog??nie
Soient E et D soit courbes elliptiques sur un corps k. Une isog??nie entre E et D est un finie morphisme f: E → D vari??t??s qui pr??serve points de base (en d'autres termes, le point sur les cartes E donn??e ?? celle sur D).
Les deux courbes sont appel??s isog??ne se il existe une isog??nie entre elles. Il se agit d'une relation d'??quivalence , sym??trie ??tant due ?? l'existence de la double isog??nie. Chaque isog??nie est un alg??brique homomorphisme et induit donc homomorphismes des groupes des courbes elliptiques pour les points k -??valu??es.
Les courbes elliptiques sur les corps finis
 .
. Soit K = F q le corps fini ?? q ??l??ments et E une courbe elliptique d??finie sur K. Alors que le pr??cise nombre de points rationnels d'une courbe elliptique E sur K est en g??n??ral assez difficile ?? calculer, Le th??or??me de Hasse sur les courbes elliptiques nous donne, y compris le point ?? l'infini, l'estimation suivante:
En d'autres termes, le nombre de points de la courbe cro??t ?? peu pr??s comme le nombre d'??l??ments dans le domaine. Ce fait peut ??tre compris et prouv?? ?? l'aide d'une th??orie g??n??rale; voir fonction zeta locale, Cohomologie ??tale.
 .
. L'ensemble des points E (F q) est un groupe ab??lien fini. Il est toujours cyclique ou le produit de deux groupes cycliques. Par exemple, la courbe d??finie par
sur F 71 a 72 points (71 points affines y compris (0,0) et une point ?? l'infini) sur ce domaine, dont le p??rim??tre est donn??e par Z / 2 Z ?? Z / Z 36. Le nombre de points sur une courbe sp??cifique peut ??tre calcul??e avec L'algorithme de Schoof.
Etudier la courbe sur la extensions de champ de F q est facilit??e par l'introduction de la fonction z??ta locale de E sur F q, d??fini par une s??rie de g??n??ration (voir ??galement ci-dessus)
o?? le corps K n est le (unique) extension de K = F q de degr?? n (ce est-?? 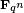 ). La fonction zeta est une fonction rationnelle dans T. Il est un nombre entier de telle sorte que
). La fonction zeta est une fonction rationnelle dans T. Il est un nombre entier de telle sorte que
Par ailleurs,
avec des nombres complexes α, β de valeur absolue 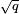 . Ce r??sultat est un cas particulier de la Conjectures de Weil. Par exemple, la fonction z??ta de
. Ce r??sultat est un cas particulier de la Conjectures de Weil. Par exemple, la fonction z??ta de 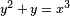 sur le corps F 2 est donn??e par
sur le corps F 2 est donn??e par 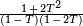 depuis la courbe a
depuis la courbe a 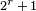 (
( 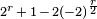 ) Points sur
) Points sur 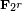 si r est impair (m??me, respectivement).
si r est impair (m??me, respectivement).
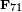 .
. Le Sato-Tate conjecture est une d??claration sur la fa??on dont le terme d'erreur 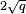 dans le th??or??me de Hasse varie avec les diff??rents nombres premiers q, si vous prenez une courbe elliptique E sur Q et r??duisez q modulo. Il a ??t?? prouv?? (pour presque tous ces courbes) en 2006 en raison des r??sultats de Taylor, Harris et Shepherd-Barron, et dit que les termes d'erreur sont ??quir??parties.
dans le th??or??me de Hasse varie avec les diff??rents nombres premiers q, si vous prenez une courbe elliptique E sur Q et r??duisez q modulo. Il a ??t?? prouv?? (pour presque tous ces courbes) en 2006 en raison des r??sultats de Taylor, Harris et Shepherd-Barron, et dit que les termes d'erreur sont ??quir??parties.
Les courbes elliptiques sur les corps finis sont notamment appliqu??es dans la cryptographie et de la factorisation de grands nombres entiers. Ces algorithmes font souvent usage de la structure de groupe sur les points de E. Algorithmes qui sont applicables ?? des groupes g??n??raux, par exemple le groupe des ??l??ments inversibles dans des domaines finis, 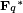 , Peut ainsi ??tre appliqu??e sur le groupe de points sur une courbe elliptique. Par exemple, le logarithme discret est un tel algorithme. L'int??r??t est que le choix d'une courbe elliptique permet une plus grande souplesse que de choisir q (et donc le groupe d'unit??s de F q). En outre, la structure de groupe de courbes elliptiques est g??n??ralement plus complexe.
, Peut ainsi ??tre appliqu??e sur le groupe de points sur une courbe elliptique. Par exemple, le logarithme discret est un tel algorithme. L'int??r??t est que le choix d'une courbe elliptique permet une plus grande souplesse que de choisir q (et donc le groupe d'unit??s de F q). En outre, la structure de groupe de courbes elliptiques est g??n??ralement plus complexe.
Algorithmes qui utilisent les courbes elliptiques
Les courbes elliptiques sur les corps finis sont utilis??s dans certains cryptographiques applications ainsi que pour factorisation entier. Typiquement, l'id??e g??n??rale de ces applications est connu qu'un algorithme qui rend l'utilisation de certains groupes finis est r????crit pour utiliser les groupes de points rationnels des courbes elliptiques. Pour plus Voir aussi:
- Cryptographie ?? courbe elliptique
- Elliptic Curve DSA
- Lenstra courbe elliptique factorisation
- Courbe elliptique primalit?? proving
Repr??sentations alternatives de courbes elliptiques
- Courbe de Hesse
- Courbe Edwards
- Courbe Twisted
- Courbe Twisted Hesse
- Courbe Twisted Edwards
- Courbe Doche-Icart-Kohel orient??e jumelage
- Courbe Doche-Icart-Kohel Triplement orient??
- Courbe jacobienne
- Courbe Montgomery
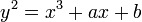
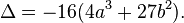
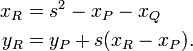
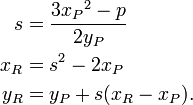
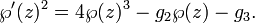
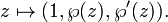
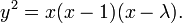
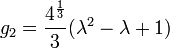
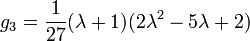
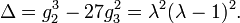
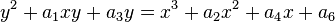
![Z (E (\ mathbf {F} _p)) = \ exp \ left (\ sum \ mathrm {carte} \ left [E ({\ mathbf F} _ {p ^ n}) \ right] \ frac {T ^ n} {n} \ right).](../../images/1230/123094.png)
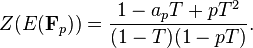
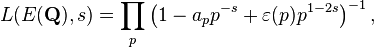
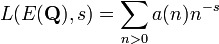
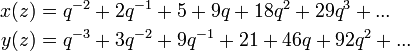
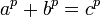
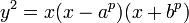
![\ Max (| x |, | y |) <\ exp \ left (\ left [10 ^ 6H \ right] ^ {{10} ^ 6} \ right).](../../images/1231/123117.png)
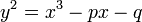
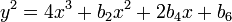
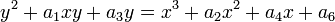
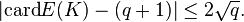
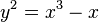
![Z (E (K), T) \ equiv \ exp \ left (\ sum_ {n = 1} ^ {\ infty} \ mathrm {carte} \ left [E (K_N) \ right] {T ^ n \ n plus } \ right)](../../images/1231/123137.png)