
Plus grand commun diviseur
?? propos de ce ??coles s??lection Wikipedia
SOS Enfants a fait cette s??lection Wikipedia aux c??t??s d'autres ??coles des ressources . Une bonne fa??on d'aider d'autres enfants est de parrainer un enfant
En math??matiques , le plus grand commun diviseur (PGCD de), parfois connu comme le plus grand facteur commun (GCF) ou un facteur plus commune (HCF), de deux non-z??ro entiers , est le plus grand entier positif qui divise les deux num??ros sans reste.
Vue d'ensemble
Le plus grand commun diviseur de a et b se ??crit pgcd (a, b), ou parfois simplement en tant que (a, b). Par exemple, gcd (12, 18) = 6, gcd (-4, 14) = 2 et pgcd (5, 0) = 5. Deux nombres sont appel??s premiers entre eux ou relativement premier si leur plus grand commun diviseur est ??gal ?? 1. Par exemple, 9 et 28 sont premiers.
Le plus grand commun diviseur est utile pour r??duire fractions vulgaires ??tre en termes plus bas. Par exemple, gcd (42, 56) = 14, par cons??quent,
Calcul du pgcd
Plus grands communs diviseurs peuvent en principe ??tre calcul?? en d??terminant le facteurs premiers des deux num??ros et comparant des facteurs, comme dans l'exemple suivant: pour calculer PGCD (18,84), on trouve les facteurs premiers 18 = 2 ?? 3 2 et 84 = 2 2 ?? 3 ?? 7 et notez que le " chevauchement "des deux expressions est 2 ?? 3; si pgcd (18,84) = 6. Dans la pratique, cette m??thode ne est possible que pour les tr??s petits nombres; calcul facteurs premiers en g??n??ral prend trop longtemps.
Un proc??d?? beaucoup plus efficace est le Algorithme d'Euclide, qui utilise le algorithme de division en combinaison avec l'observation que le pgcd de deux nombres divise aussi leur diff??rence: diviser 84 par 18 pour obtenir un quotient de 4 et un reste de 12. Ensuite, divisez 18 par 12 pour obtenir un quotient de 1 et un reste de 6 . Ensuite, divisez 12 par 6 pour obtenir un reste de 0, ce qui signifie que 6 est le pgcd.
La s??rie de quotients g??n??r??s par l'algorithme d'Euclide composer un fraction continue.
Si A et B ne sont pas tous deux z??ro, le plus grand commun diviseur de a et b peut ??tre calcul??e en utilisant moins commun multiple (LCM) de a et b:
Propri??t??s
- Chaque grand commun diviseur de a et b est un diviseur de pgcd (a, b).
- pgcd (a, b), o?? a et b sont pas tous deux z??ro, peut ??tre d??finie alternativement et de fa??on ??quivalente comme le plus petit entier positif d qui peut ??tre ??crit sous la forme d = a ?? p + B ?? q o?? p et q sont des nombres entiers . Cette expression est appel?? L'identit?? de B??zout. Num??ros de p et q comme ceci peuvent ??tre calcul??s avec le algorithme d'Euclide ??tendu.
- pgcd (a, 0) = | a |, pour a ≠ 0, ??tant donn?? que ne importe quel nombre est un diviseur de 0, et le plus grand diviseur de a est | a |. Ceci est habituellement utilis?? en tant que cas de r??f??rence ?? l'algorithme d'Euclide.
- Si a divise le produit b ?? c et pgcd (a, b) = D, puis un / d divise c.
- Si m est un entier non-n??gatif, alors pgcd (m ?? a, m ?? b) = m ?? pgcd (a, b).
- Si m est un nombre entier, alors pgcd (a + b ?? m, b) = pgcd (a, b). Si m est un diviseur commun non nul de A et B, puis pgcd (a / m, b / m) = pgcd (a, b) / m.
- Le GCD est un fonction multiplicative dans le sens suivant: si un 1 et 2 sont relativement premier, alors pgcd (a 1 ?? 2, b) = pgcd (a 1, b) ?? pgcd (a 2, b).
- Le GCD est un commutative fonction: PGCD (a, b) = pgcd (b, a).
- Le GCD est un associative fonction: pgcd (a, pgcd (b, c)) = PGCD (gcd (a, b), c).
- Le pgcd de trois chiffres peut ??tre calcul??e comme pgcd (a, b, c) = PGCD (gcd (a, b), c), ou dans quelque autre mani??re en appliquant la commutativit?? et l'associativit??. Ceci peut ??tre ??tendu ?? un nombre quelconque de nombres.
- pgcd (a, b) est ??troitement li??e ?? la LCM plus petit commun multiple (a, b): nous avons
- pgcd (a, b) ?? LCM (a, b) = a ?? b.
- Cette formule est souvent utilis??e pour calculer multiples moins communs: on calcule d'abord le PGCD avec l'algorithme d'Euclide, puis divise le produit des chiffres donn??s par leur pgcd. Les versions suivantes de Distributivit?? ??tre vrai:
- pgcd (a, LCM (b, c)) = LCM (PGCD (a, b), pgcd (a, c))
- LCM (a, pgcd (b, c)) = pgcd (LCM (a, b), LCM (a, c)).
- Il est utile de d??finir pgcd (0, 0) = 0 et LCM (0, 0) = 0 car alors les nombres naturels deviennent une complet distributif treillis avec pgcd que se rencontrent et LCM comme op??ration de jointure. Cette extension de la d??finition est ??galement compatible avec la g??n??ralisation des anneaux commutatifs ci-dessous.
- Dans un syst??me de coordonn??es cart??siennes , pgcd (a, b) peut ??tre interpr??t?? comme le nombre de points de coordonn??es int??gr??e pour la ligne droite reliant les points (0, 0) et (a, b), ?? l'exclusion (0, 0).
Probabilit??s et valeur attendue
La probabilit?? que deux entiers choisis au hasard (illimit??)  et
et 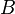 avoir un plus grand commun diviseur donn??
avoir un plus grand commun diviseur donn??  est
est  . Cela d??coule de la caract??risation de
. Cela d??coule de la caract??risation de 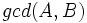 comme le nombre entier
comme le nombre entier  tel que
tel que  et
et 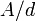 et
et  sont premiers entre eux. La probabilit?? de deux entiers partager un facteur
sont premiers entre eux. La probabilit?? de deux entiers partager un facteur  est
est 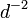 . La probabilit?? que deux entiers premiers entre eux sont est
. La probabilit?? que deux entiers premiers entre eux sont est 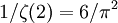 . (Voir premiers entre eux pour une d??rivation).
. (Voir premiers entre eux pour une d??rivation).
En utilisant cette information, la valeur attendue du plus grand commun diviseur de fonction peut ??tre calcul??e. C'est
Cette derni??re est la sommation S??rie harmonique, qui diverge. D'o?? la valeur attendue du plus grand commun diviseur des deux variables ne est pas bien d??finie. Ce ne est pas le cas en g??n??ral, cependant. Pour le plus grand commun diviseur de 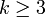 des variables, la valeur attendue est bien d??fini, et par l'argument ci-dessus, il est
des variables, la valeur attendue est bien d??fini, et par l'argument ci-dessus, il est
o??  est le Fonction z??ta de Riemann.
est le Fonction z??ta de Riemann.
Pour  , Ce est approximativement ??gale ?? 1,3684. Pour
, Ce est approximativement ??gale ?? 1,3684. Pour  , Il est d'environ 1,1106.
, Il est d'environ 1,1106.
si tous les nombres entiers x sont limit??s 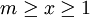 les r??sultats peuvent ??tre ??tendus ??
les r??sultats peuvent ??tre ??tendus ??
o?? 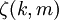 est le Fonction zeta Hurwitz.
est le Fonction zeta Hurwitz.
se ils sont diff??rents 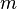 'S sont connus pour diff??rents
'S sont connus pour diff??rents  puis le meilleur
puis le meilleur 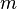 est pris.
est pris.
Le PGCD dans les anneaux commutatifs
Le plus grand commun diviseur peut plus g??n??ralement ??tre d??fini pour les ??l??ments d'un arbitraire anneau commutatif .
Si R est un anneau commutatif, et a et b sont dans R, un ??l??ment de R d est appel?? un grand commun diviseur de a et b se il divise la fois A et B (qui est, si il ya des ??l??ments x et y dans R tel que d ?? x = a et d ?? y = b). Si d est un diviseur commun de A et B, et chaque grand commun diviseur de a et b divise d, alors d est appel?? un plus grand commun diviseur de a et b.
Notez qu'avec cette d??finition, deux ??l??ments a et b peuvent tr??s bien avoir plusieurs diviseurs plus communs, ou pas du tout. Mais si R est un domaine int??grante alors toutes les deux pgcd de a et b doit ??tre ??l??ments associ??s. En outre, si R est un Anneau factoriel, puis deux ??l??ments ont un pgcd. Si R est un Domaine euclidienne alors une forme de l'algorithme d'Euclide peuvent ??tre utilis??s pour calculer diviseurs plus communs.
Ce qui suit est un exemple d'un domaine solidaire de deux ??l??ments qui ne ont pas de GCD:
Les ??l??ments 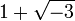 et
et 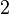 deux diviseurs communs "extr??mes" (ce est ?? dire ne importe quel diviseur commun qui est un multiple de 2 est associ?? ?? deux, il en est de m??me pour
deux diviseurs communs "extr??mes" (ce est ?? dire ne importe quel diviseur commun qui est un multiple de 2 est associ?? ?? deux, il en est de m??me pour 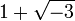 ), Mais ils ne sont pas associ??s, donc il n'y a pas de plus grand commun diviseur de a et b.
), Mais ils ne sont pas associ??s, donc il n'y a pas de plus grand commun diviseur de a et b.
Correspondant ?? la propri??t?? Bezout nous peut, en tout anneau commutatif, envisager la collecte des ??l??ments de la forme  , O?? p et q gamme sur l'anneau. Ceci est le id??al engendr?? par a et b, et est not?? tout simplement
, O?? p et q gamme sur l'anneau. Ceci est le id??al engendr?? par a et b, et est not?? tout simplement 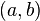 . Dans un anneau dont tous les id??aux sont les principaux (un anneau principal ou PID), cet id??al sera identique ?? l'ensemble des multiples de certains ??l??ments de l'anneau D; puis ce d est un plus grand commun diviseur de a et b. Mais l'id??al
. Dans un anneau dont tous les id??aux sont les principaux (un anneau principal ou PID), cet id??al sera identique ?? l'ensemble des multiples de certains ??l??ments de l'anneau D; puis ce d est un plus grand commun diviseur de a et b. Mais l'id??al 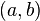 peuvent ??tre utiles, m??me lorsqu'il n'y a pas plus grand commun diviseur de a et b. (En Effet, Ernst Kummer utilis?? cet id??al comme un remplacement pour un GCD dans son traitement de dernier th??or??me de Fermat , bien qu'il l'envisageait comme l'ensemble des multiples de certains hypoth??tique ou id??al, ??l??ment annulaire d, d'o?? le terme de cycle th??orique.)
peuvent ??tre utiles, m??me lorsqu'il n'y a pas plus grand commun diviseur de a et b. (En Effet, Ernst Kummer utilis?? cet id??al comme un remplacement pour un GCD dans son traitement de dernier th??or??me de Fermat , bien qu'il l'envisageait comme l'ensemble des multiples de certains hypoth??tique ou id??al, ??l??ment annulaire d, d'o?? le terme de cycle th??orique.)

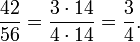
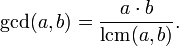
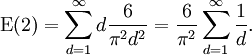
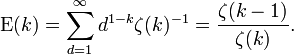
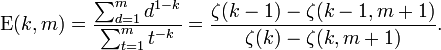
![R = \ mathbb {Z} \ left [\ sqrt {-3} \ right], \ quad a = 4 = 2 \ cdot 2 = \ left (1+ \ sqrt {-3} \ right) \ left (1- \ sqrt {-3} \ right), \ quad b = \ left (1+ \ sqrt {-3} \ right) \ cdot 2.](../../images/184/18487.png)
