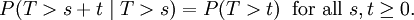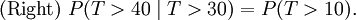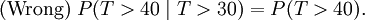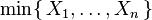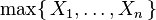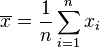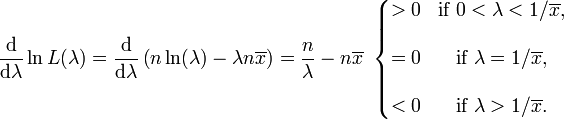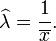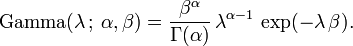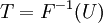Distribution exponentielle

Contexte des ??coles Wikip??dia

SOS Enfants, un organisme de bienfaisance de l'??ducation , a organis?? cette s??lection. Avec enfants SOS vous pouvez choisir de parrainer des enfants dans plus de cent pays

Exponentiel
Densit?? de probabilit??
Fonction de distribution cumulative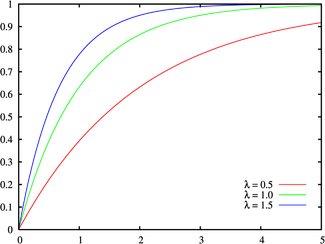
Param??tres	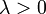$\ Lambda> 0 \,$ taux ou ??chelle inverse ( r??el )
Soutien	$[0, \ infty) \!$
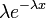PDF	$\ Lambda e ^ {- \ lambda x}$
CDF	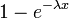$1 - e ^ {- \ lambda x}$
Signifier	$\ Frac {1} {\ lambda} \,$
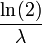M??diane	$\ Frac {\ ln (2)} {\ lambda} \,$
Mode	$0 \,$
Variance	$\ Lambda ^ {- 2} \,$
Asym??trie	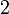$2 \,$
Ex. aplatissement	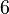$6 \,$
Entropy	$1 - \ ln (\ lambda) \,$
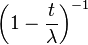MGF	$\ Left (1 - \ frac {t} {\ lambda} \ right) ^ {- 1} \,$
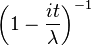FC	$\ Left (1 - \ frac {it} {\ lambda} \ right) ^ {- 1} \,$

Dans la th??orie des probabilit??s et des statistiques , les distributions exponentielles sont une classe de continues distributions de probabilit?? . Une distribution exponentielle se pose naturellement lors de la mod??lisation du temps entre les ??v??nements ind??pendants qui se produisent ?? un taux moyen constant.

Caract??risation

Densit?? de probabilit??

Le fonction de densit?? de probabilit?? (pdf) d'une distribution exponentielle est de la forme

$f (x; \ lambda) = \ \ left {\ begin {matrix} \ lambda e ^ {- \ lambda} x &, \; x \ ge 0, 0 \\ & \; x <0. \ end {matrix} \ right.$

o?? λ> 0 est un param??tre de distribution, souvent appel?? le param??tre de d??bit. La distribution est support?? sur l'intervalle [0, ∞). Si une variable al??atoire X a cette distribution, nous ??crire X ~ exponentiel (λ).

Fonction de distribution cumulative

Le fonction de distribution cumulative est donn??e par

$F (x; \ lambda) = \ \ left {\ begin {matrix} 1-e ^ {- \ lambda} x &, \; x \ ge 0, 0 \\ & \; x <0. \ end {matrix} \ right.$

Param??trage suppl??ant

Une alternative param??trage est couramment utilis?? pour d??finir le fonction de densit?? de probabilit?? (pdf) d'une distribution exponentielle

$f (x; \ beta) = \ \ left {\ begin {matrix} \ frac {1} {\ beta} e ^ {- x / \ beta} &, \; x \ ge 0, 0 \\ & \; x <0. \ end {matrix} \ right.$

o?? β> 0 est un param??tre d'??chelle de la distribution et est le r??ciproque du param??tre de vitesse, λ, d??finis ci-dessus. Dans cette description, β est un param??tre de survie dans ce sens que si une variable al??atoire X est la dur??e de temps pendant laquelle un syst??me biologique ou m??canique donn??e M parvient ?? survivre et X ~ exponentielle (β), puis $\ Mathbb {} E [X] = \ beta$ . Ce est-??-dire la dur??e pr??vue de la survie des unit??s M est β de temps.

Cette sp??cification autre est parfois plus pratique que celle donn??e ci-dessus, et certains auteurs se utiliser comme une d??finition standard. Nous ne assumons cette sp??cification autre. Malheureusement, cela donne lieu ?? un l'ambigu??t?? de notation. En g??n??ral, le lecteur doit v??rifier lequel de ces deux sp??cifications est utilis?? si un auteur ??crit "X ~ exponentiel (λ)", soit depuis la notation dans la pr??c??dente (en utilisant λ) ou la notation dans cette section (ici, en utilisant β pour ??viter toute confusion) pourrait ??tre pr??vu.

Pr??sence et applications

La distribution exponentielle se produit naturellement dans la description de la longueur des temps inter-arriv??es homog??ne dans un Processus de Poisson.

La distribution exponentielle peut ??tre consid??r?? comme un homologue continu de la distribution g??om??trique, qui d??crit le nombre de Bernoulli n??cessaires pour un processus discret changement d'??tat. En revanche, la distribution exponentielle d??crit le temps pour un proc??d?? en continu pour changer d'??tat.

Dans les sc??narios du monde r??el, l'hypoth??se d'un taux constant (ou la probabilit?? par unit?? de temps) est rarement satisfait. Par exemple, le taux d'appels t??l??phoniques entrants est diff??rente selon le moment de la journ??e. Mais si nous nous concentrons sur un intervalle de temps pendant laquelle le taux est ?? peu pr??s constante, tels que 2-4 heures en jours de travail, la distribution exponentielle peut ??tre utilis?? comme un bon mod??le approximatif pour le moment jusqu'?? ce que le prochain appel t??l??phonique arrive. R??serves similaires se appliquent aux exemples suivants qui donnent les variables approximativement exponentielle distribu??s:

le temps jusqu'?? ce qu'une particule radioactive se d??sint??gre, ou le temps entre les signaux sonores d'un compteur Geiger;
le temps qu'il faut avant votre prochain appel t??l??phonique
le temps jusqu'?? ce d??faut (sur le paiement aux d??tenteurs de la dette de l'entreprise) sous forme r??duite mod??lisation du risque de cr??dit

Les variables exponentielles peuvent ??galement ??tre utilis??s pour mod??liser des situations o?? certains ??v??nements se produisent avec une probabilit?? constante par unit?? de distance:

la distance entre mutations sur un ADN brin;
la distance entre roadkill sur une rue donn??e;

En la th??orie des files, les temps entre les arriv??es (c.-??-temps entre les clients entrent dans le syst??me) sont souvent mod??lis??s comme des variables r??parties de fa??on exponentielle. La longueur d'un processus qui peut ??tre consid??r?? comme une s??quence de plusieurs t??ches ind??pendantes est mieux mod??lis??e par une variable apr??s la Distribution d'Erlang (qui est la distribution de la somme de plusieurs variables ind??pendantes r??parties de fa??on exponentielle).

la th??orie de la fiabilit?? et de ing??nierie de la fiabilit?? ??galement faire usage extensif de la distribution exponentielle. En raison de l' absence de m??moire propri??t?? de cette distribution, il est bien adapt?? pour mod??liser la constante partie de taux de risque de la courbe en baignoire utilis??e dans la th??orie de la fiabilit??. Il est ??galement tr??s pratique car il est si facile d'ajouter les taux d'??chec dans un mod??le de fiabilit??. La distribution exponentielle est cependant pas appropri??e pour mod??liser la dur??e de vie globale des organismes ou des dispositifs techniques, parce que les "taux d'??chec" ici ne sont pas constantes: plus d'??checs se produisent pour les tr??s jeunes et pour les tr??s vieux syst??mes.

Dans la physique , si vous observez un gaz ?? un prix fixe de temp??rature et pression dans un uniforme champ gravitationnel, les hauteurs des diff??rentes mol??cules suivent ??galement une distribution exponentielle approximative. Ceci est une cons??quence de la propri??t?? mentionn??e ci-dessous entropique.

Propri??t??s

Moyenne et la variance

La moyenne ou valeur attendue d'une variable al??atoire X distribu?? de fa??on exponentielle avec le param??tre de taux λ est donn??e par

$\ Mathrm {} E [X] = \ frac {1} {\ lambda}. \!$

?? la lumi??re des exemples donn??s ci-dessus, cela fait sens: si vous recevez des appels t??l??phoniques ?? un taux moyen de 2 par heure, alors vous pouvez vous attendre ?? attendre une demi-heure pour chaque appel.

La variance de X est donn??e par

$\ Mathrm {} Var [X] = \ frac {1} {\ lambda ^ 2}. \!$

Perte de m??moire

Une propri??t?? importante de la distribution exponentielle est qu'il est sans m??moire. Cela signifie que si une variable al??atoire T est distribu?? de fa??on exponentielle, de sa ob??it probabilit??s conditionnelles

$P (T> s + t \; | \; T> s) = P (T> t) \; \; \ Hbox {} pour tous les \ s, t \ ge 0.$

Ce dit que le probabilit?? conditionnelle que nous devons attendre, par exemple, plus de 10 secondes avant la premi??re arriv??e, ??tant donn?? que la premi??re arriv??e n'a pas encore pass?? apr??s 30 secondes, ne est pas diff??rent de la probabilit?? initiale que nous devons attendre plus de 10 secondes pour la premi??re arriv??e. Ce est souvent mal compris par les ??tudiants qui suivent des cours sur la probabilit??: le fait que P (T> 40 | T> 30) = P (T> 10) ne signifie pas que les ??v??nements T> 40 et T> 30 sont ind??pendante. Pour r??sumer: "Perte de m??moire" de la distribution de probabilit?? du d??lai d'attente T jusqu'?? ce que les premiers moyens d'arriv??e

$\ Mathrm {(droite)} \ P (T> 40 \ mi T> 30) = P (T> 10).$

Cela ne signifie pas

$\ Mathrm {(Mauvais)} \ P (T> 40 \ mi T> 30) = P (T> 40).$

(Ce serait l'ind??pendance. Ces deux ??v??nements ne sont pas ind??pendants.)

Les distributions exponentielles et la distributions g??om??triques sont les seules distributions de probabilit?? sans m??moire.

La distribution exponentielle a ??galement une constante fonction de risque.

Quartiles

La fonction quantile (fonction de distribution cumulative inverse) pour exponentiel (λ) est

$F ^ {- 1} (p; \ lambda) = \ frac {- \ ln (1-p)} {\ lambda}, \!$

pour 0 ≤ p <1. Le quartiles sont donc:

premier quartile: $\ Ln (4/3) / \ lambda \,$
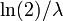
m??diane: $\ Ln (2) / \ lambda \,$
troisi??me quartile: $\ Ln (4) / \ lambda \,$

Kullback-Leibler

La sc??ne Kullback-Leibler entre Exp (λ ₀₎ (??vraie?? distribution) et Exp (λ) (??rapprochant?? distribution) est donn??e par

$\ Delta (\ lambda || \ lambda_0) = \ log (\ lambda) - \ log (\ lambda_0) + \ frac {\ lambda_0} {\ lambda} - 1.$

Distribution d'entropie maximale

Parmi toutes les distributions de probabilit??s continues avec le soutien [0, ∞) et μ dire, la distribution exponentielle avec λ = 1 / μ a plus grand entropie.

R??partition du minimum de variables al??atoires exponentielles

Soit X _1, ..., X _n soit variables al??atoires ind??pendantes distribu??es de fa??on exponentielle avec des param??tres de taux λ _1, ..., λ _n. Puis

$\ Min \ {\, X_1, \ dots, X_n \, \}$

est ??galement une distribution exponentielle, avec le param??tre

$\ Lambda = \ lambda_1 + \ cdots + \ lambda_n. \,$

Cependant,

$\ Max \ {\, X_1, \ dots, X_n \, \}$

ne est pas une distribution exponentielle.

Estimation des param??tres

Supposons que vous savez qu'une variable donn??e est distribu?? de fa??on exponentielle et que vous voulez estimer le param??tre de taux λ.

Maximum de vraisemblance

Le fonction de vraisemblance pour λ, ??tant donn?? un ??chantillon ind??pendant et identiquement distribu??es x = (x _1, ..., x _n) tir?? de votre variable, est

$L (\ lambda) = \ prod_ {i = 1} ^ n \ lambda \, \ exp (- \ lambda x_i) = \ lambda ^ n \, \ exp \ \ left (\ -! \ Lambda \ {i sum_ = 1} ^ n x_i \ right) = \ lambda ^ n \ exp \ gauche (- \ lambda n \ overline {x} \ right),$

o??

$\ Overline {x} = {1 \ over n} \ sum_ {i = 1} ^ n x_i$

est la moyenne d'??chantillon.

Le d??riv?? du logarithme de la fonction de vraisemblance est

$\ Frac {\ mathrm {d}} {\ mathrm {d} \ lambda} \ ln L (\ lambda) = \ frac {\ mathrm {d}} {\ mathrm {d} \ lambda} \ left (n \ ln (\ lambda) - \ lambda n \ overline {x} \ right) = {n \ over \ lambda} -n \ overline {x} \ \ \ left {\ begin {matrix}> 0 et \ mbox {if} \ 0 <\ lambda <1 / \ overline {x}, \\ \\ = 0 & \ mbox {if} \ \ lambda = 1 / \ overline {x}, \\ \\ <0 et \ mbox {if} \ \ lambda> 1 / \ overline {x}. \ End {matrix} \ right.$

En cons??quence, la estimation du maximum de vraisemblance pour le param??tre de vitesse est

$\ Widehat {\ lambda} = \ frac1 {\ overline {x}}.$

Inf??rence bay??sienne

Le conjugu?? pr??alable pour la distribution exponentielle est la la distribution gamma (dont la distribution exponentielle est un cas particulier). Le param??trage suivants du gamma pdf est utile:

$\ Mathrm {Gamma} (\ lambda \,; \, \ alpha, \ beta) = \ frac {\ beta ^ {\ alpha}} {\ Gamma (\ alpha)} \, \ lambda ^ {\ alpha-1} \, \ exp (- \ lambda \, \ beta). \!$

Le distribution a posteriori p peut alors ??tre exprim??e en termes de la fonction de vraisemblance d??fini ci-dessus et un gamma avant:

$p (\ lambda) \ propto L (\ lambda) \ times \ mathrm {Gamma} (\ lambda \,; \, \ alpha, \ beta)$

$= \ Lambda ^ n \, \ exp (- \ lambda \, n \ overline {x}) \ times \ frac {\ beta ^ {\ alpha}} {\ Gamma (\ alpha)} \, \ lambda ^ {\ alpha-1} \, \ exp (- \ lambda \, \ beta)$

$\ Propto \ lambda ^ {(\ alpha + n) -1} \, \ exp (- \ lambda \, (\ beta + n \ overline {x})).$

Maintenant, la densit?? a posteriori p a ??t?? d??termin??s jusqu'?? une constante de normalisation manquantes. Comme il a la forme d'un gamma pdf, ce qui peut facilement ??tre rempli, et l'on obtient

$p (\ lambda) = \ mathrm {Gamma} (\ lambda \,; \, \ alpha + n, \ beta + n \ overline {x}).$

Ici, les param??tres α peut ??tre interpr??t?? comme le nombre d'observations ant??rieures, β et que la somme des observations ant??rieures.

G??n??ration variables al??atoires exponentielles

Une m??thode conceptuellement tr??s simple pour g??n??rer exponentielle variables al??atoires sont bas??es sur le transformation inverse ??chantillonnage: ??tant donn?? une variable al??atoire U tir?? de la distribution uniforme sur l'intervalle unit?? 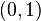$(0, 1)$ , La variable al??atoire

$T = F ^ {- 1} (U) \!$

suit une loi exponentielle, o?? $F ^ {- 1}$ est la fonction quantile, d??fini par

$F ^ {- 1} (p) = \ frac {- \ ln (1-p)} {\ lambda}. \!$

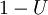En outre, si U est uniforme sur $(0; 1)$ , Alors il en est $1-U$ . Cela signifie qu'on peut g??n??rer des variables al??atoires exponentielles comme suit:

$T = \ frac {- \ ln U} {\ lambda}. \!$

Autres m??thodes pour g??n??rer des variables al??atoires exponentielles sont examin??s par Knuth et Devroye.

Le algorithme de ziggourat est une m??thode rapide pour g??n??rer des variables al??atoires exponentielles.

Distributions connexes

Une distribution exponentielle est un cas particulier d'un la distribution gamma avec 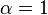$\ Alpha = 1$ (Ou $k = 1$ en fonction du jeu de param??tres utilis??).
?? la fois une distribution exponentielle et une distribution gamma sont des cas particuliers de la la distribution de type phase.
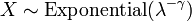$Y \ sim \ {operatorname Weibull} (\ gamma, \ lambda)$ , Soit Y a un Distribution de Weibull, si $Y = X ^ {1 / \ gamma} \,$ et $X \ sim \ {operatorname exponentielle} (\ lambda ^ {- \ gamma})$ . En particulier, toutes les distributions exponentielle est ??galement une distribution de Weibull.
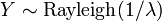$Y \ sim \ operatorname {} Rayleigh (1 / \ lambda)$ , Soit Y a un Distribution de Rayleigh, si 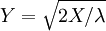$Y = \ sqrt {2X / \ lambda}$ et $X \ sim \ {operatorname exponentielle} (\ lambda)$ .
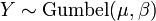$Y \ sim \ operatorname {} Gumbel (\ mu, \ beta)$ , Soit Y a un Distribution de Gumbel si $Y = \ mu - \ beta \ log (X / \ lambda) \,$ et $X \ sim \ {operatorname exponentielle} (\ lambda)$ .
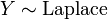$Y \ sim \ {operatorname Laplace}$ , Soit Y a un La distribution de Laplace, si 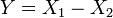$Y = X_1 - X_2 \,$ pour deux distributions exponentielles ind??pendantes $X_1 \,$ et $X_2 \,$ .
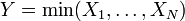$Y \ sim \ {operatorname exponentielle}$ , Soit Y suit une loi exponentielle si $Y = \ min (x_1, \ dots, X_n)$ pour les distributions exponentielles ind??pendantes $X_i \,$ .
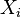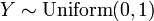$Y \ sim \ operatorname {} uniforme (0,1)$ , Soit Y a un distribution uniforme si $Y = \ exp (-X \ lambda) \,$ et $X \ sim \ {operatorname exponentielle} (\ lambda)$ .
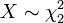$X \ sim \ chi_2 ^ 2$ , C.-??-X a une distribution chi-carr?? avec deux degr??s de libert??, le cas $X \ sim \ {operatorname exponentielle} (\ lambda = 1/2) \, \;$ .
Laisser $X_1 \ dots X_n \ sim \ {operatorname exponentielle} (\ lambda), \$ ??tre distribu??s de fa??on exponentielle et ind??pendante $Y = \ sum_ {i = 1} ^ n X_i \,$ . Puis $Y \ sim \ {gamma} operatorname (n, 1 / \ lambda) \,$
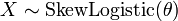$X sim \ {operatorname SkewLogistic} (\ theta) \ \,$ , Puis $\ Operatorname {} log (1 + e ^ {- X}) \ sim \ {operatorname exponentielle} (\ theta) \,$

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Exponential_distribution&oldid=195091990 "