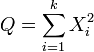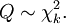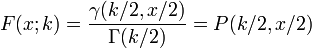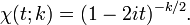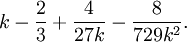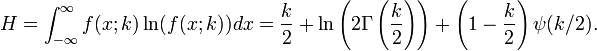La distribution Chi-squared
Saviez-vous ...
Cette s??lection ??coles a ??t?? choisi par SOS Enfants pour les ??coles dans le monde en d??veloppement ne ont pas acc??s ?? Internet. Il est disponible en t??l??chargement intranet. SOS Children travaille dans 45 pays africains; pouvez-vous aider un enfant en Afrique ?
Densit?? de probabilit?? 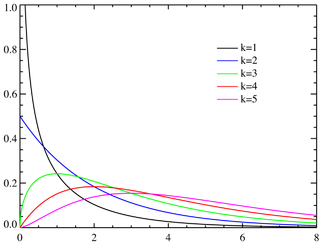 | |
Fonction de distribution cumulative 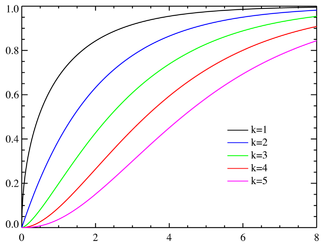 | |
| Param??tres | 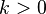 degr??s de libert?? degr??s de libert?? |
|---|---|
| Soutien | 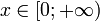 |
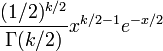 | |
| CDF |  |
| Signifier | 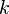 |
| M??diane | environ 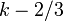 |
| Mode | 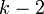 si si 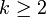 |
| Variance | 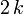 |
| Asym??trie |  |
| Ex. aplatissement | 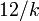 |
| Entropy |  |
| MGF | 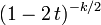 pour pour 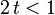 |
| FC | 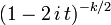 |
Dans la th??orie des probabilit??s et des statistiques , la distribution du chi carr?? (aussi chi carr?? ou 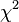 distribution) est l'un des plus largement utilis??s th??oriques des distributions de probabilit?? en inf??rence statistique, par exemple, dans tests de signification statistique. Il est utile parce que, sous des hypoth??ses raisonnables, les quantit??s calcul??es peuvent ??tre facilement prouv?? qu'ils ont des distributions qui approximatives ?? la distribution du chi carr?? si le hypoth??se nulle est vraie.
distribution) est l'un des plus largement utilis??s th??oriques des distributions de probabilit?? en inf??rence statistique, par exemple, dans tests de signification statistique. Il est utile parce que, sous des hypoth??ses raisonnables, les quantit??s calcul??es peuvent ??tre facilement prouv?? qu'ils ont des distributions qui approximatives ?? la distribution du chi carr?? si le hypoth??se nulle est vraie.
Si 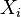 sont k , ind??pendants normalement distribu??s variables al??atoires moyenne 0 et de variance 1, alors la variable al??atoire
sont k , ind??pendants normalement distribu??s variables al??atoires moyenne 0 et de variance 1, alors la variable al??atoire
est distribu??e selon la distribution du chi carr??. Ce est g??n??ralement ??crite
La distribution du chi carr?? a un param??tre: 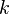 - Un nombre entier positif qui sp??cifie le nombre de degr??s de libert?? (ce est ?? dire le nombre de
- Un nombre entier positif qui sp??cifie le nombre de degr??s de libert?? (ce est ?? dire le nombre de 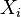 )
)
La distribution du chi carr?? est un cas particulier de la la distribution gamma.
Les situations les plus connus dans lesquels la distribution du chi carr?? sont utilis??s sont la commune des tests chi-carr??s pour qualit?? de l'ajustement d'une distribution observ??e ?? un th??orique, et de la ind??pendance des deux crit??res de classification des donn??es qualitatives. Cependant, de nombreux autres tests statistiques conduisent ?? une utilisation de cette distribution. Un exemple est L'analyse de Friedman de la variance par rangs.
Caract??ristiques
Densit?? de probabilit??
Un fonction de densit?? de probabilit?? de la distribution du chi carr?? est
o??  d??signe le Fonction Gamma, qui prend valeurs particuli??res aux demi-entiers.
d??signe le Fonction Gamma, qui prend valeurs particuli??res aux demi-entiers.
Fonction de distribution cumulative
Son fonction de distribution cumulative est la suivante:
o?? 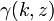 est le fonctions inf??rieur incompl??te Gamma et
est le fonctions inf??rieur incompl??te Gamma et 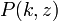 est le fonction Gamma r??gularis??e.
est le fonction Gamma r??gularis??e.
Tables de cette distribution - souvent dans sa forme cumulative - sont largement disponibles et la fonction est inclus dans de nombreux des feuilles de calcul et tous les progiciels statistiques.
Fonction caract??ristique
Le fonction caract??ristique de la distribution chi carr?? est
Propri??t??s
La distribution du chi carr?? a de nombreuses applications en inf??rence statistique , par exemple dans des tests chi-carr??s et ?? l'estimation des ??carts . Il entre dans le probl??me de l'estimation de la moyenne d'une population distribu??e normalement et le probl??me de l'estimation de la pente d'une r??gression ligne via son r??le dans la distribution t de Student . Il entre tout analyse des probl??mes de la variance par son r??le dans le F-distribution, qui est la distribution du rapport de deux khi-deux ind??pendants des variables al??atoires r??parties par leurs degr??s respectifs de libert??.
Approximation normale
Si  , Alors que
, Alors que 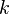 tend vers l'infini, la distribution de
tend vers l'infini, la distribution de 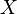 tend ?? la normalit??. Cependant, la tendance est lente (l'asym??trie est
tend ?? la normalit??. Cependant, la tendance est lente (l'asym??trie est 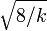 et l'exc??s de kurtosis est
et l'exc??s de kurtosis est 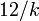 ) Et deux transformations sont g??n??ralement consid??r??s, dont chacun se rapproche plus rapide que la normale
) Et deux transformations sont g??n??ralement consid??r??s, dont chacun se rapproche plus rapide que la normale 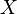 m??me:
m??me:
Fisher empirique a d??montr?? que 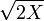 est approximativement normale de moyenne
est approximativement normale de moyenne 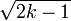 et de variance unit??. Il est possible d'arriver au m??me r??sultat d'approximation normale en utilisant instant correspondant. Pour le voir, consid??rer la moyenne et la variance d'une variable al??atoire Chi-distribu??s
et de variance unit??. Il est possible d'arriver au m??me r??sultat d'approximation normale en utilisant instant correspondant. Pour le voir, consid??rer la moyenne et la variance d'une variable al??atoire Chi-distribu??s 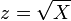 , Qui sont donn??s par
, Qui sont donn??s par 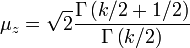 et
et 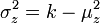 O??
O?? 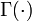 est la fonction Gamma. Le rapport particulier des fonctions Gamma dans
est la fonction Gamma. Le rapport particulier des fonctions Gamma dans 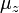 a le d??veloppement en s??rie suivant :
a le d??veloppement en s??rie suivant :
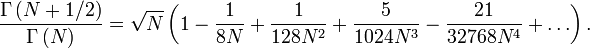 Quand
Quand 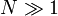 , Ce rapport peut ??tre approch??e comme suit:
, Ce rapport peut ??tre approch??e comme suit: 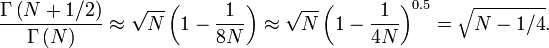
Alors, simple moment r??sultats correspondants dans l'approximation suivante 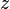 :
: 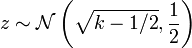 D'o?? il r??sulte que
D'o?? il r??sulte que 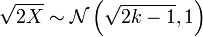 .
.
Wilson et Hilferty ont montr?? en 1931 que ![\ Sqrt [3] {X / k}](../../images/185/18595.png) est approximativement normale de moyenne
est approximativement normale de moyenne 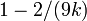 et la variance
et la variance  .
.
Le valeur attendue d'une variable al??atoire ayant une distribution chi-carr?? avec 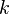 degr??s de libert?? est
degr??s de libert?? est 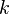 et la variance est
et la variance est  . La m??diane est donn??e approximativement par
. La m??diane est donn??e approximativement par
Notez que les deux degr??s de libert?? conduit ?? une distribution exponentielle .
Entropie de l'information
Le entropie de l'information est donn??e par
o?? 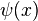 est le Fonction digamma.
est le Fonction digamma.
Distributions connexes
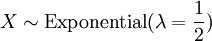 est une distribution exponentielle si
est une distribution exponentielle si 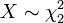 (Avec 2 degr??s de libert??).
(Avec 2 degr??s de libert??). 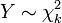 est une distribution de chi-carr?? si
est une distribution de chi-carr?? si 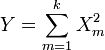 pour
pour 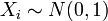 ind??pendante qui sont normalement distribu?? .
ind??pendante qui sont normalement distribu?? . - Si le
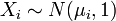 disposer de moyens non nuls, puis
disposer de moyens non nuls, puis 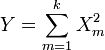 est tir?? ?? partir d'un distribution chi-carr?? non centrale.
est tir?? ?? partir d'un distribution chi-carr?? non centrale. - La distribution du chi carr??
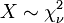 est un cas particulier de la la distribution gamma, en ce que
est un cas particulier de la la distribution gamma, en ce que 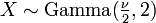 .
.  est un F-distribution si
est un F-distribution si 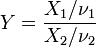 o??
o?? 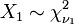 et
et 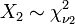 sont ind??pendants avec leurs degr??s respectifs de libert??.
sont ind??pendants avec leurs degr??s respectifs de libert??. 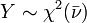 est une distribution de chi-carr?? si
est une distribution de chi-carr?? si 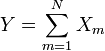 o??
o??  sont ind??pendants et
sont ind??pendants et 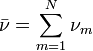 .
. - si
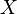 est chi carr?? distribu??,
est chi carr?? distribu??, 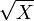 est chi distribu??.
est chi distribu??. - en particulier, si
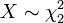 (Chi-carr?? avec deux degr??s de libert??), puis
(Chi-carr?? avec deux degr??s de libert??), puis 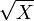 est Rayleigh distribu??.
est Rayleigh distribu??. - si
 sont iid
sont iid 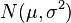 variables al??atoires , puis
variables al??atoires , puis 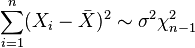 o??
o??  .
. - si
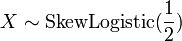 , Puis
, Puis 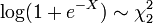
| Nom | Statistique |
|---|---|
| la distribution chi-carr?? | 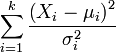 |
| chi carr?? non centrale de distribution | 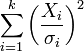 |
| la distribution chi | 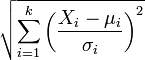 |
| distribution chi non centrale |  |