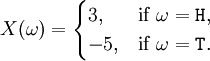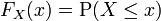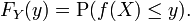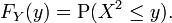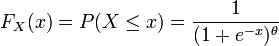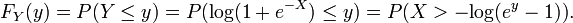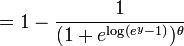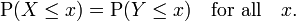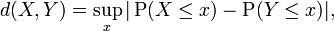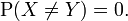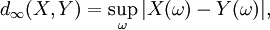Variable al??atoire

?? propos de ce ??coles s??lection Wikipedia

SOS croit que l'??ducation donne une meilleure chance dans la vie des enfants dans le monde en d??veloppement aussi. Pour comparer les organismes de bienfaisance de parrainage ce est le meilleur lien de parrainage .

Une variable al??atoire est une abstraction de la notion intuitive de chances dans les domaines des math??matiques th??oriques, formant les bases de la th??orie des probabilit??s et statistiques math??matiques.

La th??orie et la langue de variables al??atoires ont ??t?? formalis??s au cours des derniers si??cles aux c??t??s id??es de probabilit??. Familiarit?? compl??te avec toutes les propri??t??s de variables al??atoires n??cessite une solide exp??rience dans les concepts d??velopp??s plus r??cemment de th??orie de la mesure, mais variables al??atoires peuvent ??tre compris intuitivement ?? diff??rents niveaux de la fluidit?? en math??matiques; la th??orie des ensembles et de calcul sont fondamentaux.

De fa??on g??n??rale, une variable al??atoire est d??finie comme une quantit?? dont les valeurs sont al??atoires et ?? laquelle une distribution de probabilit?? est assign??e. Plus formellement, une variable al??atoire est une ?? partir d'une fonction mesurable ??chantillon espace pour le mesurable espace des valeurs possibles de la variable. La d??finition formelle de variables al??atoires place exp??riences impliquant r??sultats valeurs r??elles r??solument dans le mesurer la th??orie cadre et nous permet de construire des fonctions de distribution de variables al??atoires ?? valeurs r??elles.

Exemples

Une variable al??atoire peut ??tre utilis?? pour d??crire le processus de laminage une foire mourir et les r??sultats possibles {1, 2, 3, 4, 5, 6}. La repr??sentation la plus ??vidente est de prendre ce jeu comme l'espace d'??chantillon, la mesure de probabilit?? d'??tre mesure uniforme, et la fonction d'??tre le fonction identit??.

Pour un tirage au sort, un espace appropri?? des r??sultats possibles est Ω = {H, T} (pour les t??tes et queues). Un exemple variable al??atoire sur cet espace est

$X (\ omega) = \ begin {} 3 cas, & \ text {if} \ omega = \ texttt {H}, \\ -5, & \ text {if} \ omega = \ texttt {T}. \ End {} cas$

Variables al??atoires ?? valeurs r??elles

Typiquement, l'espace mesurable est l'espace mesurable sur les nombres r??els. Dans ce cas, laissez- $(\ Omega, \ mathcal {F}, P)$ ??tre un espace de probabilit?? . Ensuite, la fonction $X: \ Omega \ rightarrow \ mathbb {R}$ est une variable al??atoire r??elle valeur-si

$\ {\ Omega: X (\ omega) \ le r \} \ in \ mathcal {F} \ qquad \ forall r \ in \ mathbb {R}$

Les fonctions de distribution de variables al??atoires

Association d'une fonction de distribution cumulative (CDF) avec une variable al??atoire est une g??n??ralisation de l'affectation d'une valeur ?? une variable. Si le CDF est un (?? droite continue) Fonction de Heaviside alors la variable prend la valeur du saut, avec une probabilit?? 1. En g??n??ral, le CDF sp??cifie la probabilit?? que la variable prend des valeurs particuli??res.

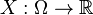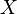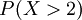Si une variable al??atoire $X: \ Omega \ to \ mathbb {R}$ d??finie sur l'espace de probabilit?? $(\ Omega, A, P)$ est donn??e, nous pouvons poser des questions comme "Quelle est la probabilit?? que la valeur de $X$ est plus grand que 2? ". Ce est la m??me que la probabilit?? de l'??v??nement $\ {S \ in \ Omega: X (s)> 2 \}$ qui est souvent ??crit comme $P (X> 2)$ en abr??g??.

L'enregistrement de toutes ces probabilit??s de plages de sortie d'une valeur r??elle variable al??atoire X donne la distribution de probabilit?? de X. La distribution de probabilit?? ??oublie?? sur l'espace de probabilit?? notamment utilis??s pour d??finir X et seulement enregistre les probabilit??s de diff??rentes valeurs de X. Une telle distribution de probabilit?? peut toujours ??tre captur?? par son fonction de distribution cumulative

$F_X (x) = \ operatorname {P} (X \ le x)$

et parfois aussi ?? l'aide d'un fonction de densit?? de probabilit??. En mesurer la th??orie termes, nous utilisons la variable al??atoire X pour "pousser en avant" la mesure P sur Ω ?? une mesure d F sur R. Le Ω de l'espace de probabilit?? sous-jacente est un dispositif technique utilis?? pour garantir l'existence de variables al??atoires, et parfois de les construire. Dans la pratique, on dispose souvent de la Ω total de l'espace et juste met une mesure sur R qui attribue mesure 1 ?? l'ensemble de la ligne r??elle, ce est ?? dire, on travaille avec des distributions de probabilit??s au lieu de variables al??atoires.

Moments

La distribution de probabilit?? d'une variable al??atoire est souvent caract??ris?? par un petit nombre de param??tres, qui ont ??galement une interpr??tation pratique. Par exemple, il est souvent assez pour savoir ce que son "valeur moyenne" est. Ce est captur?? par le concept math??matique de valeur attendue d'une variable al??atoire, not?? E [X]. En g??n??ral, E [f (X)] ne est pas ??gale ?? f (E [X]). Une fois que la "valeur moyenne" est connu, on pourrait alors se demander comment loin de cette valeur moyenne des valeurs de X sont typiquement, une question qui est r??pondu par la variance et l'??cart-type d'une variable al??atoire.

Math??matiquement, cela est connu comme le (g??n??ralis??e) probl??me de moments: pour une classe donn??e de variables al??atoires X, trouver une collection {f _i} de fonctions telles que l'attente valeurs E [f _i (X)] caract??riser compl??tement la distribution de la variable al??atoire X.

Fonctions de variables al??atoires

Si nous avons une variable al??atoire X sur Ω et un fonction mesurable f: R → R, alors Y = f (X) sera ??galement une variable al??atoire sur Ω, puisque la composition des fonctions mesurables est ??galement mesurable. La m??me proc??dure qui a permis ?? une de passer d'un espace de probabilit?? (Ω, P) de (R, dF _X) peut ??tre utilis?? pour obtenir la distribution de Y. Le fonction de distribution cumulative de Y est

$F_Y (y) = \ operatorname {P} (f (X) \ le y).$

Exemple 1

Soit X, une valeur r??elle variable al??atoire continue et laissez Y = X ^2. Ensuite,

$F_Y (y) = \ operatorname {P} (X ^ 2 \ le y).$

Si y <0, alors P (X ² ≤ y) = 0, de sorte que

$F_Y (y) = 0 \ qquad \ hbox {if} \ quad y <0.$

Si y ≥ 0, alors

$\ Operatorname {P} (X ^ 2 \ le y) = \ operatorname {P} (| X | \ le \ sqrt {y}) = \ operatorname {P} (- \ sqrt {y} \ le X \ le \ sqrt {y}),$

$F_Y (y) = F_X (\ sqrt {y}) - F_X (- \ sqrt {y}) \ qquad \ hbox {if} \ quad y \ ge 0.$

Exemple 2

Supposer 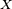$\ Scriptstyle X$ est une variable al??atoire avec une distribution cumulative

$F_ {X} (x) = P (X \ leq x) = \ frac {1} {(1 + e ^ {- x}) ^ {\ theta}}$

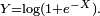o?? $\ Scriptstyle \ theta> 0$ est un param??tre fixe. Consid??rons la variable al??atoire $\ Scriptstyle Y = \ mathrm {} log (1 + e ^ {- X}).$ Ensuite,

$F_ {Y} (y) = P (Y \ leq y) = P (\ mathrm {} log (1 + e ^ {- X}) \ leq y) = P (X> - \ mathrm {} log (e ^ {y} -. 1)) \,$

La derni??re expression peut ??tre calcul?? en fonction de la r??partition de $X,$ si

$F_ {Y} (y) = 1 - F_ {X} (- \ mathrm {Journal} (e ^ {y} - 1)) \,$

$= 1 - \ frac {1} {(1 + e ^ {\ mathrm {} log (e ^ {y} - 1)}) ^ {\ theta}}$

$= 1 - \ frac {1} {(1 + e ^ {y} - 1) ^ {\ theta}}$

$= 1 - e ^ {- y \ theta} \,.$

Equivalence des variables al??atoires

Il ya plusieurs sens diff??rents dans lesquels les variables al??atoires peuvent ??tre consid??r??es comme ??quivalentes. Deux variables al??atoires peuvent ??tre ??gaux, ??gale presque s??rement, ??gaux en moyenne, ou l'??quivalent dans la distribution.

Dans l'ordre croissant de la force, la d??finition pr??cise de ces notions d'??quivalence est donn??e ci-dessous.

L'??galit?? dans la distribution

Deux variables al??atoires X et Y sont ??gaux dans la distribution si elles ont les m??mes fonctions de distribution:

$\ Operatorname {P} (X \ le x) = \ operatorname {P} (Y \ le x) \ quad \ hbox {} pour tous les \ quad x.$

Deux variables al??atoires ayant ??gale fonctions g??n??ratrices des moments ont la m??me distribution. Ceci permet, par exemple, une m??thode utile de v??rifier l'??galit?? de certaines fonctions du iidrv de.

Pour ??tre ??gal dans la distribution, variables al??atoires ne doivent pas ??tre d??finis sur le m??me espace de probabilit??. La notion d'??quivalence dans la distribution est associ??e ?? la notion suivante de distance entre les distributions de probabilit??,

$d (X, Y) = \ sup_x | \ operatorname {P} (X \ le x) - \ operatorname {P} (Y \ le x) |,$

qui est la base de la Test de Kolmogorov-Smirnov.

L'??galit?? dans moyen

Deux variables al??atoires X et Y sont ??gaux ?? p-i??me dire si la p-i??me instant de | X - Y | est ??gal ?? z??ro, ce est-

$\ Operatorname {} E (| X-Y | ^ p) = 0.$

L'??galit?? dans p e moyenne implique l'??galit?? dans q ??me moyenne pour tout q <p. Comme dans le cas pr??c??dent, il existe une distance connexe entre les variables al??atoires, ?? savoir

$D_P (X, Y) = \ {E} operatorname (| X-Y | ^ p).$

??galit?? presque s??re

Deux variables al??atoires X et Y sont ??gaux presque certainement si, et seulement si, la probabilit?? qu'ils sont diff??rents est ??gal ?? z??ro:

$\ Operatorname {P} (X \ neq Y) = 0.$

?? toutes fins pratiques dans la th??orie des probabilit??s, cette notion d'??quivalence est aussi forte que l'??galit?? r??elle. Il est associ?? ?? la distance suivante:

$d_ \ infty (X, Y) = \ sup_ \ omega | X (\ omega) -Y (\ omega) |,$

o?? 'sup' dans ce cas repr??sente la borne sup??rieure essentiel au sens de th??orie de la mesure.

??galit??

Enfin, les deux variables al??atoires X et Y sont ??gaux si elles sont ??gales en tant que fonctions de leur espace de probabilit??, qui est,

$X (\ omega) = Y (\ omega) \ qquad \ hbox {} pour tous les \ quad \ omega$

Convergence

Beaucoup de statistiques math??matiques consiste ?? prouver les r??sultats de convergence pour certaines s??quences de variables al??atoires; voir par exemple le loi des grands nombres et le th??or??me central limite.

Il existe diff??rents sens dans lequel une s??quence (X _n) de variables al??atoires peuvent converger ?? une variable al??atoire X. Elles sont expliqu??es dans l'article sur convergence des variables al??atoires.

Litt??rature

Kallenberg, O., mesures al??atoires, 4e ??dition. Academic Press, New York, Londres; Akademie-Verlag, Berlin (1986). MR0854102 ISBN 0123949602
Papoulis, Athanasios 1965 Probabilit??, variables al??atoires et les processus stochastiques. McGraw-Hill Kogakusha, Tokyo, 9e ??dition, ISBN 0-07-119981-0.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Random_variable&oldid=195646641 "