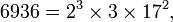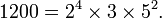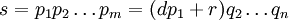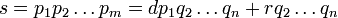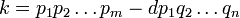Th??or??me fondamental de l'arithm??tique
Saviez-vous ...
SOS Enfants a essay?? de rendre le contenu plus accessible Wikipedia par cette s??lection des ??coles. Les enfants SOS est le plus grand don de charit?? du monde enfants orphelins et abandonn??s la chance de la vie familiale.
Dans la th??orie des nombres , le th??or??me fondamental de l'arithm??tique (ou uniques-prime-factorisation th??or??me) stipule que chaque nombre naturel sup??rieur ?? 1 peut ??tre ??crit comme un produit unique de nombres premiers . Par exemple,
Il n'y a pas d'autres possibles factorisations de 6936 ou 1200 dans les nombres premiers. La repr??sentation ci-dessus se effondre r??p??t?? facteurs premiers en pouvoirs pour faciliter l'identification. Parce que la multiplication est commutative et associative , l'ordre des facteurs ne est pas pertinent et le plus souvent ??crite, du moins au plus grand.
De nombreux auteurs prennent les nombres naturels ?? commencer par 0, qui n'a pas de facteurs premiers. Ainsi Th??or??me 1 de Hardy & Wright (1979) prend la forme, "Chaque entier positif, sauf une, est un produit de nombres premiers", et le th??or??me 2 (leur ??fondamentales??) affirme unicit??. Le num??ro 1 ne est pas se amorcer, mais puisque ce est le produit d'aucun chiffre, il est souvent pratique de l'inclure dans le th??or??me par le vide r??gle du produit. (Voir, par exemple, Calcul du pgcd .)
Hardy & Wright d??finissent un nombre anormal d'??tre un nombre hypoth??tique qui ne poss??de pas une factorisation unique. Ils prouvent le th??or??me fondamental de l'arithm??tique en prouvant qu'il ne existe pas un nombre anormal.
Applications
Le th??or??me fondamental de l'arithm??tique ??tablit l'importance des nombres premiers. Les nombres premiers sont les blocs de construction de base de tout nombre entier positif, en ce sens que chaque entier positif peut ??tre construit ?? partir du produit de nombres premiers avec une construction unique. Trouver la factorisation d'un entier permet d??rivation de tous ses diviseurs, ?? la fois premiers et non-prime.
Par exemple, au-dessus de la factorisation de 6936 montre que ne importe quel diviseur positif de 6936 doit avoir la forme  O??
O??  prend l'une des quatre valeurs dans {0, 1, 2, 3}, o??
prend l'une des quatre valeurs dans {0, 1, 2, 3}, o?? 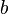 prend l'une des deux valeurs dans {0, 1}, et o??
prend l'une des deux valeurs dans {0, 1}, et o??  prend l'une des valeurs 3 dans {0, 1, 2}. En multipliant le nombre d'options ind??pendantes ensemble produit un total de
prend l'une des valeurs 3 dans {0, 1, 2}. En multipliant le nombre d'options ind??pendantes ensemble produit un total de  diviseurs positifs.
diviseurs positifs.
Une fois que les facteurs premiers de deux nombres sont connus, leur plus grand commun diviseur et moins commun multiple peut ??tre trouv?? rapidement. Par exemple, ?? partir de ce qui pr??c??de, il est montr?? que le plus grand commun diviseur de 6936 et 1200 est 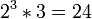 . Toutefois, si les facteurs premiers ne sont pas connus, l'utilisation de la Euclidienne algorithme n??cessite g??n??ralement beaucoup moins de calculs que l'affacturage les deux num??ros.
. Toutefois, si les facteurs premiers ne sont pas connus, l'utilisation de la Euclidienne algorithme n??cessite g??n??ralement beaucoup moins de calculs que l'affacturage les deux num??ros.
Le th??or??me fondamental garantit que additif et multiplicatif fonctions arithm??tiques sont compl??tement d??termin??es par leurs valeurs sur les pouvoirs des nombres premiers.
Preuve
Le th??or??me ??tait pratiquement prouv?? par Euclide , mais la premi??re preuve compl??te et correcte se trouve dans le Disquisitiones Arithmeticae par Carl Friedrich Gauss . Il peut ??tre important de noter que les Egyptiens aiment Ahm??s utilis?? aspects pratiques de la t??t affacturage, et plus petit commun multiple, du th??or??me fondamental de l'arithm??tique permettant une longue tradition de d??velopper, formalis??e par Euclide, et rigoureusement prouv??e par Gauss.
Bien qu'?? premi??re vue le th??or??me semble ????vident??, il ne tient pas dans les syst??mes num??riques plus g??n??rales, y compris de nombreux anneaux de entiers alg??briques. Ce fut d'abord fait remarquer par Ernst Kummer en 1843, dans son ouvrage sur le dernier th??or??me de Fermat . La reconnaissance de cet ??chec est l'un des premiers d??veloppements dans th??orie alg??brique des nombres.
La preuve d'Euclid
La preuve consiste en deux ??tapes. Dans la premi??re ??tape chaque nombre se av??re ??tre un produit de z??ro ou plusieurs nombres premiers. Dans le second, la preuve montre que les deux repr??sentations peuvent ??tre unifi??es en une seule repr??sentation.
Num??ros de composites non-prime
Supposons qu'il y ait un nombre entier positif qui ne peut ??tre ??crit comme un produit de nombres premiers. Ensuite, il doit y avoir un plus petit nombre aussi (voir bien-commande): que ce soit n. Ce nombre n ne peut pas ??tre 1, en raison de la Convention vide-produit ci-dessus. Il ne peut pas ??tre un nombre premier soit, puisque tout nombre premier est un produit d'une seule ??coute, lui-m??me. Donc, il doit ??tre un nombre compos??. Ainsi
- n = ab
o?? a et b sont des entiers positifs plus petits que n. Puisque n est le plus petit nombre qui ne peut ??tre ??crit comme un produit de nombres premiers, a et b peuvent ??tre ??crites comme des produits de nombres premiers. Mais alors
- n = ab
peut ??tre ??crit comme un produit de nombres premiers, ainsi, un la preuve par l'absurde. C'est un minime contre-argument.
M??thode de descente infinie
Une preuve de l'unicit?? de la d??composition en facteurs premiers d'un utilisations enti??res donn??es descente infinie: Supposons qu'un certain entier peut ??tre ??crit comme (au moins) deux diff??rents produits de nombres premiers: alors il doit exister un petit entier  avec une telle propri??t??. Notons ces deux factorisations de
avec une telle propri??t??. Notons ces deux factorisations de  comme
comme 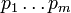 et
et 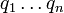 , Tel que
, Tel que  .
.
Aucun  (Avec
(Avec 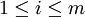 ) Peut ??tre ??gale ?? ne importe quel
) Peut ??tre ??gale ?? ne importe quel 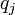 (Avec
(Avec  ), Car il y aurait autrement un entier plus petit factorisable de deux fa??ons (en ??liminant les facteurs premiers communs dans les deux produits), en violation de l'hypoth??se ci-dessus. Maintenant, on peut supposer sans perte de g??n??ralit?? que
), Car il y aurait autrement un entier plus petit factorisable de deux fa??ons (en ??liminant les facteurs premiers communs dans les deux produits), en violation de l'hypoth??se ci-dessus. Maintenant, on peut supposer sans perte de g??n??ralit?? que  est un facteur premier plus petit que ne importe quel
est un facteur premier plus petit que ne importe quel 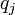 (Avec
(Avec  ). Laisser
). Laisser  le quotient et
le quotient et  la reste de la division
la reste de la division 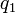 par
par  . Par le algorithme de division
. Par le algorithme de division  et
et  sont garantis ??tre entiers tels que
sont garantis ??tre entiers tels que 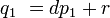 et
et  . Notez que
. Notez que  ne peut pas ??tre
ne peut pas ??tre  , Car ce serait faire
, Car ce serait faire 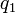 un multiple de
un multiple de  et pas premier. Aussi
et pas premier. Aussi  Car
Car 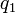 est sup??rieur ??
est sup??rieur ??  .
.
Substituant dans des 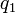 dans la d??finition initiale des
dans la d??finition initiale des  ci-dessus,
ci-dessus,
Par distributivit??:
D??finir un nouvel entier 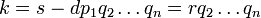 . Depuis
. Depuis  , Il est clair que
, Il est clair que  doit ??tre inf??rieure ??
doit ??tre inf??rieure ??  . Et puisque
. Et puisque  ,
,  doit ??tre positif. D'apr??s la d??finition de
doit ??tre positif. D'apr??s la d??finition de  Il se ensuit que:
Il se ensuit que:
et par factorisation  :
:
Il ya donc une factorisation premi??re  qui comprend
qui comprend  . Mais il est ??galement vrai que
. Mais il est ??galement vrai que
Depuis  ,
,  ne peut pas ??tre un facteur premier de
ne peut pas ??tre un facteur premier de  . Ainsi, en combinant les facteurs premiers de
. Ainsi, en combinant les facteurs premiers de  avec
avec  Il est ??galement possible de construire une factorisation de
Il est ??galement possible de construire une factorisation de  qui ne comprend pas
qui ne comprend pas  . Donc
. Donc  a deux facteurs premiers diff??rents, contredisant l'hypoth??se originale qui
a deux facteurs premiers diff??rents, contredisant l'hypoth??se originale qui  est le plus petit entier factorisable en plus d'une fa??on. Ainsi, l'hypoth??se de d??part doit ??tre fausse.
est le plus petit entier factorisable en plus d'une fa??on. Ainsi, l'hypoth??se de d??part doit ??tre fausse.