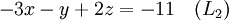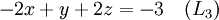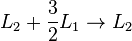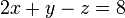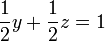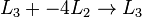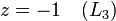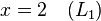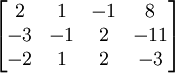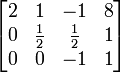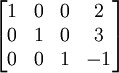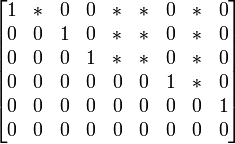??limination de Gauss
?? propos de ce ??coles s??lection Wikipedia
Cette s??lection ??coles a ??t?? choisi par SOS Enfants pour les ??coles dans le monde en d??veloppement ne ont pas acc??s ?? Internet. Il est disponible en t??l??chargement intranet. SOS Enfants a regard?? des enfants en Afrique depuis quarante ans. Pouvez-vous aider dans leur travail en Afrique ?
En alg??bre lin??aire , ??limination de Gauss est une algorithme qui peut ??tre utilis?? pour d??terminer les solutions d'un syst??me d'??quations lin??aires , de trouver la un rang de matrice , et pour calculer l'inverse d'un matrice carr??e inversible. ??limination de Gauss est nomm?? d'apr??s le math??maticien et scientifique allemand Carl Friedrich Gauss .
Op??rations ??l??mentaires sur les lignes sont utilis??es dans l'algorithme. L'algorithme comporte deux parties, dont chacun consid??re les lignes de la matrice dans l'ordre. La premi??re partie r??duit la matrice Matrice ??chelonn??e tandis que le second r??duit la matrice ?? la suite de forme r??duite de Gauss. La premi??re partie seule est suffisante pour de nombreuses applications.
Un algorithme connexes, mais moins efficace, Gauss-Jordan ??limination, apporte une matrice ?? forme r??duite de Gauss en un seul passage.
Histoire
La m??thode d'??limination de Gauss appara??t dans le chapitre huit, rectangulaires tableaux, de l'importante chinoise texte math??matique ou Jiuzhang suanshu Les Neuf Chapitres sur l'art math??matique. Son utilisation est illustr??e sur dix-huit probl??mes, de deux ?? cinq ??quations. La premi??re r??f??rence ?? l'ouvrage de ce titre est dat?? ?? 179 CE, mais certaines parties ont ??t?? ??crites d??s environ 150 BCE.
Cependant, la m??thode a ??t?? invent??e en Europe ind??pendamment. Il est nomm?? d'apr??s le math??maticien Carl Friedrich Gauss .
Aper??u Algorithme
Le processus d'??limination gaussienne comporte deux parties. La premi??re partie (avant ??limination) r??duit un syst??me donn?? soit triangulaire ou forme ??chelonn??e, ou les r??sultats dans un ??quation d??g??n??r?? sans solution, indiquant que le syst??me n'a pas de solution. Ceci est accompli par l'utilisation de op??rations ??l??mentaires sur les lignes. Les utilisations seconde ??tape substitution en arri??re pour trouver la solution du syst??me ci-dessus.
D??clar?? ??quivalente pour les matrices, la premi??re partie r??duit ?? une matrice rang??e forme ??chelon aide op??rations ??l??mentaires sur les lignes tandis que le second, il se r??duit ?? forme r??duite de Gauss, ou ramer forme canonique.
Un autre point de vue, qui se av??re ??tre tr??s utile d'analyser l'algorithme, ce est que l'??limination de Gauss calcule une matrice d??composition. Les trois op??rations ??l??mentaires sur les lignes utilis??es dans l'??limination de Gauss (multiplication de lignes, la commutation de lignes, et en ajoutant un multiple de lignes ?? d'autres lignes) montant ?? la multiplication de la matrice d'origine avec des matrices inversibles de la gauche. La premi??re partie de l'algorithme calcule une LU d??composition, tandis que la deuxi??me partie ??crit la matrice d'origine comme le produit d'une matrice inversible uniquement d??termin?? et un r??duit matrice rang??e ??chelonn??e uniquement d??termin??e.
Exemple
Supposons que le but est de trouver et de d??crire la solution (s), le cas ??ch??ant, de ce qui suit syst??me d'??quations lin??aires :
L'algorithme est le suivant: ?? ??liminer  ?? partir de toutes les ??quations ci-dessous
?? partir de toutes les ??quations ci-dessous 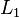 , Puis ??liminer
, Puis ??liminer 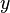 ?? partir de toutes les ??quations ci-dessous
?? partir de toutes les ??quations ci-dessous 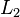 . Cela mettra le syst??me en forme triangulaire. Puis, en utilisant de nouveau la substitution, chaque inconnu peut ??tre r??solue pour.
. Cela mettra le syst??me en forme triangulaire. Puis, en utilisant de nouveau la substitution, chaque inconnu peut ??tre r??solue pour.
Dans notre exemple, nous ??liminons  ?? partir de
?? partir de 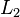 en ajoutant
en ajoutant 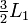 ??
?? 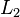 , Puis nous ??liminons
, Puis nous ??liminons  ?? partir de
?? partir de 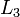 en ajoutant
en ajoutant 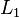 ??
?? 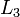 . Formellement:
. Formellement:
Le r??sultat est le suivant:
Maintenant, nous ??liminons 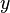 ?? partir de
?? partir de 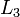 en ajoutant
en ajoutant  ??
?? 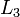 :
:
Le r??sultat est le suivant:
Ce r??sultat est un syst??me d'??quations lin??aires en forme triangulaire, de sorte que la premi??re partie de l'algorithme est termin??.
La deuxi??me partie, back-substitution, consiste ?? r??soudre pour les inconnues dans l'ordre inverse. Ainsi, nous pouvons facilement voir que
Ensuite, 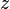 peut ??tre substitu?? en
peut ??tre substitu?? en 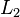 , Qui peut ensuite ??tre r??solu facilement obtenir
, Qui peut ensuite ??tre r??solu facilement obtenir
Suivant, 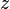 et
et 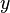 peut ??tre substitu?? en
peut ??tre substitu?? en 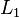 , Qui peut ??tre r??gl?? pour obtenir
, Qui peut ??tre r??gl?? pour obtenir
Ainsi, le syst??me est r??gl??.
Cet algorithme fonctionne pour ne importe quel syst??me d'??quations lin??aires. Il est possible que le syst??me ne peut pas ??tre r??duite ?? la forme triangulaire, mais toujours avoir au moins une solution valable: par exemple, si 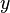 ne est pas survenu dans
ne est pas survenu dans 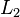 et
et 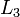 apr??s notre premi??re ??tape ci-dessus, l'algorithme aurait ??t?? incapable de r??duire le syst??me ?? la forme triangulaire. Toutefois, il serait encore r??duit le syst??me de forme ??chelonn??e. Dans ce cas, le syst??me n'a pas de solution unique, car il contient au moins un variable libre. L'ensemble de la solution peut alors ??tre exprim?? param??trique (ce est, en termes de variables libres, de sorte que si les valeurs pour les variables libres sont choisis, une solution sera g??n??r??).
apr??s notre premi??re ??tape ci-dessus, l'algorithme aurait ??t?? incapable de r??duire le syst??me ?? la forme triangulaire. Toutefois, il serait encore r??duit le syst??me de forme ??chelonn??e. Dans ce cas, le syst??me n'a pas de solution unique, car il contient au moins un variable libre. L'ensemble de la solution peut alors ??tre exprim?? param??trique (ce est, en termes de variables libres, de sorte que si les valeurs pour les variables libres sont choisis, une solution sera g??n??r??).
En pratique, on ne traite pas habituellement avec les syst??mes r??els en termes des ??quations, mais fait plut??t l'utilisation de la matrice augment??e (ce qui est ??galement appropri?? pour des manipulations informatiques). Ce, alors, est l'algorithme gaussien appliqu?? ?? l'??limination augment??e matrice du syst??me ci-dessus, commen??ant par:
qui, ?? la fin de la premi??re partie de l'algorithme se pr??sente comme suit:
Ce est ?? dire qu'il se trouve dans formulaire de Gauss.
A la fin de l'algorithme, on se retrouve avec
Ce est ?? dire qu'il se trouve dans forme r??duite de Gauss de, ou la ligne forme canonique.
D'autres applications
Trouver l'inverse d'une matrice
Supposer  est un
est un 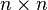 Matrix et vous avez besoin de calculer sa inverse. Le
Matrix et vous avez besoin de calculer sa inverse. Le 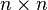 matrice d'identit?? est augment??e vers la droite de
matrice d'identit?? est augment??e vers la droite de  , Formant une
, Formant une  matrice (le matrice de bloc
matrice (le matrice de bloc ![B = [A, I]](../../images/142/14234.png) ). Gr??ce ?? l'application des op??rations ??l??mentaires sur les lignes et l'algorithme d'??limination gaussienne, le bloc de gauche de
). Gr??ce ?? l'application des op??rations ??l??mentaires sur les lignes et l'algorithme d'??limination gaussienne, le bloc de gauche de 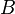 peut ??tre r??duite ?? la matrice d'identit??
peut ??tre r??duite ?? la matrice d'identit?? 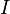 , Ce qui laisse
, Ce qui laisse 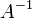 dans le bloc de droite de
dans le bloc de droite de 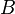 .
.
Si l'algorithme est incapable de r??duire  ?? la forme triangulaire, puis
?? la forme triangulaire, puis  ne est pas inversible.
ne est pas inversible.
Dans la pratique, inversant une matrice est rarement n??cessaire. La plupart du temps, on ne est vraiment apr??s que la solution d'un syst??me d'??quations lin??aires particulier.
L'algorithme g??n??ral pour calculer les rangs et bases
L'algorithme d'??limination gaussienne peut ??tre appliqu??e ?? ne importe quel 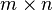 matrice
matrice  . Si nous obtenons ??coinc??s?? dans une colonne donn??e, nous passons ?? la colonne suivante. De cette fa??on, par exemple, certaines
. Si nous obtenons ??coinc??s?? dans une colonne donn??e, nous passons ?? la colonne suivante. De cette fa??on, par exemple, certaines  matrices peuvent ??tre transform??s en une matrice qui a une rang??e forme ??chelonn??e r??duite comme
matrices peuvent ??tre transform??s en une matrice qui a une rang??e forme ??chelonn??e r??duite comme
(Les * s 'sont des entr??es arbitraires). Cette matrice d'??chelon 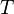 contient une mine d'informations sur
contient une mine d'informations sur  : Le rang de
: Le rang de  est 5 car il existe cinq rang??es non nulles dans
est 5 car il existe cinq rang??es non nulles dans 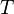 ; l' espace vectoriel engendr?? par les colonnes de
; l' espace vectoriel engendr?? par les colonnes de  a une base constitu??e de la premi??re, troisi??me, quatri??me, septi??me et neuvi??me colonne de
a une base constitu??e de la premi??re, troisi??me, quatri??me, septi??me et neuvi??me colonne de  (les colonnes de celles de
(les colonnes de celles de 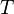 ), Et le * 's vous dire comment les autres colonnes de
), Et le * 's vous dire comment les autres colonnes de  peut se ??crire comme des combinaisons lin??aires des colonnes de base.
peut se ??crire comme des combinaisons lin??aires des colonnes de base.
Analyse
??limination de Gauss sur une matrice n ?? n n??cessite environ 2 n 3/3 op??rations. Donc, il a une complexit?? de 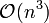 .
.
Cet algorithme peut ??tre utilis?? sur un ordinateur pour les syst??mes avec des milliers d'??quations et d'inconnues. Cependant, le co??t devient prohibitif pour les syst??mes avec des millions d'??quations. Ces grands syst??mes sont g??n??ralement r??solus en utilisant m??thodes it??ratives. M??thodes sp??cifiques existent pour les syst??mes dont les coefficients suivent un sch??ma r??gulier (voir syst??me d'??quations lin??aires ).
L'??limination de Gauss peut ??tre effectu??e sur tout domaine.
??limination de Gauss est num??riquement stable pour diagonale dominante ou matrices d??finies positives. Pour les matrices g??n??rales, ??limination de Gauss est g??n??ralement consid??r?? comme stable dans la pratique si vous utilisez pivot partiel tel que d??crit ci-dessous, m??me si il ya des exemples pour lesquels il est instable.
Pseudocode
Comme expliqu?? ci-dessus, l'??limination de Gauss ??crit une donn??e m ?? n matrice A uniquement comme un produit d'un m ?? m inversible matrice S et une matrice de Gauss T. Ici, S est le produit des matrices correspondant aux op??rations effectu??es en rang??e.
L'algorithme pour calculer formelle 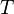 ?? partir de
?? partir de  suit. Nous ??crivons
suit. Nous ??crivons ![A [i, j]](../../images/142/14240.png) pour l'entr??e dans la rang??e
pour l'entr??e dans la rang??e  , Colonne
, Colonne  en matrice
en matrice  . La transformation est effectu??e ??en place??, ce qui signifie que la matrice originale
. La transformation est effectu??e ??en place??, ce qui signifie que la matrice originale  est perdu et successivement remplac?? par
est perdu et successivement remplac?? par 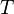 .
.
i := 1 j := 1 while (i ≤ m and j ≤ n) do Find pivot in column j, starting in row i: maxi := i for k := i+1 to m do if abs(A[k,j]) > abs(A[maxi,j]) then maxi := k end if end for if A[maxi,j] ≠ 0 then swap rows i and maxi, but do not change the value of i Now A[i,j] will contain the old value of A[maxi,j]. divide each entry in row i by A[i,j] Now A[i,j] will have the value 1. for u := i+1 to m do subtract A[u,j] * row i from row u Now A[u,j] will be 0, since A[u,j] - A[i,j] * A[u,j] = A[u,j] - 1 * A[u,j] = 0. end for i := i + 1 end if j := j + 1 end while Cet algorithme diff??re l??g??rement de celui ??voqu?? plus t??t, parce que avant d'??liminer une variable, il ??change des premi??res rang??es pour d??placer l'entr??e avec la plus grande valeur absolue ?? la "position de pivot". Tel que proc??dure de pivotement permet d'am??liorer la stabilit?? num??rique de l'algorithme; certaines variantes sont ??galement en cours d'utilisation.
La colonne en cours de transformation est appel??e la colonne de pivotement. Proc??dez de gauche ?? droite, laissant la colonne pivot soit la premi??re colonne, puis la deuxi??me colonne, etc. et enfin la derni??re colonne avant la ligne verticale. Pour chaque colonne pivot, faire les deux ??tapes suivantes avant de passer ?? la colonne pivot suivante:
- Recherchez l'??l??ment en diagonale dans la colonne de pivot. Cet ??l??ment est appel?? pivot. La ligne contenant le pivot est appel?? la ligne de pivot. Diviser chaque ??l??ment de la ligne pivot par le pivot d'obtenir une nouvelle ligne de pivot avec un 1 dans la position de pivot.
- Obtenir un 0 ?? chaque position au-dessous de la position de pivotement en soustrayant un multiple appropri?? de la ligne de pivotement de chacune des rang??es au-dessous.
?? l'issue de cette proc??dure, la matrice augment??e sera en forme ??chelonn??e et peut ??tre r??solu en arri??re-substitution.