Calcul vectoriel

Contexte des ??coles Wikip??dia

SOS Enfants produite ce site pour les ??coles ainsi que ce site de vid??o sur l'Afrique . Voir http://www.soschildren.org/sponsor-a-child pour conna??tre le parrainage d'enfants.

Calcul vectoriel (??galement appel??e analyse vectorielle) est un domaine de math??matiques concern?? avec multivari??e analyse r??elle des vecteurs dans un l'espace interne du produit de deux ou plus dimensions (quelques r??sultats - ceux qui concernent la produit en croix - ne peuvent ??tre appliqu??s ?? trois dimensions). Il se compose d'une suite de formules et de r??solution de probl??mes techniques tr??s utiles pour l'ing??nierie et de la physique . Analyse vectorielle a son origine dans analyse de quaternion, et a ??t?? formul??e par l'ing??nieur et scientifique am??ricain J. Willard Gibbs et l'ing??nieur britannique Oliver Heaviside.

Calcul vectoriel concerne champs scalaires, qui associent un scalaire ?? chaque point dans l'espace, et champs de vecteurs, qui associent un vecteur ?? chaque point dans l'espace. Par exemple, la temp??rature d'une piscine est un champ scalaire: ?? chaque point nous associons une valeur scalaire de la temp??rature. Le d??bit d'eau dans le m??me pool est un champ de vecteurs: ?? chaque point nous associons un vecteur vitesse.

op??rations vectorielles

Vecteur ??tudes de calcul diff??rents op??rateurs diff??rentiels d??finis sur les champs scalaires ou vectorielles, qui sont g??n??ralement exprim??s en termes de del op??rateur ( $\ Nabla$ ). Les quatre op??rations les plus importantes dans le calcul vectoriel sont:

Op??ration	Notation	Description	Domaine / Plage
Pente	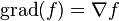$\ {Operatorname grad} (f) = \ nabla f$	Mesure la vitesse et la direction du changement dans un champ scalaire.	Cartes champs scalaires ?? des champs de vecteurs.
Curl	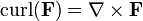$\ {Operatorname boucle} (\ mathbf {F}) = \ nabla \ times \ mathbf {F}$	Mesure la tendance ?? tourner autour d'un point dans un champ de vecteur.	Cartes champs de vecteurs ?? des champs de vecteurs.
Divergence	$\ {Div} operatorname (\ mathbf {F}) = \ nabla \ cdot \ mathbf {F}$	Mesure la magnitude d'une source ou un puits ?? un moment donn?? dans un champ de vecteurs.	Cartes champs de vecteurs ?? des champs scalaires.
Laplacien	$\ Delta f = \ nabla ^ 2 f = \ nabla \ cdot \ nabla f$	Composition des op??rations de divergence et gradient.	Cartes champs scalaires ?? des champs scalaires.

Une quantit?? appel??e le Jacobienne est utile pour ??tudier les fonctions lorsque les deux le domaine et de la fonction sont ?? variables multiples, comme un changement de variables lors de l'int??gration.

Th??or??mes

De m??me, il ya plusieurs th??or??mes importants li??s ?? ces op??rateurs qui g??n??ralisent le th??or??me fondamental du calcul ?? des dimensions sup??rieures:

Th??or??me	D??claration	Description
Th??or??me du gradient	$\ Varphi \ left (\ mathbf {q} \ right) - \ varphi \ left (\ mathbf {p} \ right) = \ int_L \ nabla \ varphi \ cdot d \ mathbf {r}.$	Le int??grale curviligne ?? travers un champ de gradient (vecteur) est ??gale ?? la diff??rence de son champ scalaire aux extr??mit??s de la courbe .
Le th??or??me de Green	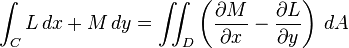$\ Int_ {C} L \, dx + M \, dy = \ iint_ {D} \ left (\ frac {\ partial M} {\ x partielle} - \ frac {\ partial L} {\ y partielle} \ right ) \, dA$	L'int??grale de la courbure d'un champ scalaire vectoriel sur une r??gion dans le plan est ??gale ?? l'int??grale de ligne du champ de vecteurs sur la courbe limitant la r??gion.
Th??or??me de Stokes	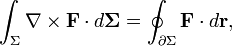$\ Int _ {\ Sigma} \ nabla \ times \ mathbf {F} \ cdot d \ mathbf {\ Sigma} = \ oint _ {\ partial \ Sigma} \ mathbf {F} \ cdot d \ mathbf {r},$	L'int??grale de la boucle d'un champ de vecteurs sur une surface est ??gale ?? l'int??grale de ligne du champ de vecteurs sur la courbe d??limitant la surface.
Th??or??me de la divergence	$\ Iiint \ limits_V \ left (\ nabla \ cdot \ mathbf {F} \ right) dV = \ iint \ limites _ {\ partie V} \ mathbf {F} \ cdot d \ mathbf {S},$	L'int??grale de la divergence d'un champ vectoriel sur certaines solide est ??gale ?? l'int??grale de la flux ?? travers la surface d??limitant le solide.

L'utilisation de calcul vectoriel peut exiger l'impartialit?? de la syst??me de coordonn??es ?? prendre en compte (voir produit en croix et impartialit?? pour plus de d??tails). La plupart des r??sultats analytiques sont faciles ?? comprendre, sous une forme plus g??n??rale, en utilisant le m??canisme de la g??om??trie diff??rentielle , dont le calcul vectoriel forme un sous-ensemble.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Vector_calculus&oldid=201811633 "