Distance

Renseignements g??n??raux

Enfants SOS offrent un chargement complet de la s??lection pour les ??coles pour une utilisation sur les intranets des ??coles. Parrainer un enfant de faire une r??elle diff??rence.

La distance est une description num??rique de quelle distance les objets sont. Dans la physique ou de la discussion de tous les jours, la distance peut se r??f??rer ?? une longueur physique, une p??riode de temps, ou une estimation bas??e sur d'autres crit??res (par exemple, "deux comt??s plus"). En math??matiques , la distance doit r??pondre ?? des crit??res plus rigoureux.

Dans la plupart des cas, il existe une sym??trie et ??distance de A ?? B" est interchangeable avec "la distance entre B et A".

Math??matiques

G??om??trie

En g??om??trie neutre, la distance minimale entre deux points est la longueur du segment de droite entre eux.

Dans la g??om??trie analytique , la distance entre deux points du plan xy peuvent ??tre trouv??es en utilisant la formule de distance. La distance entre (x _1, y ₁₎ et (x _2, y ₂₎ est donn??e par

$d = \ sqrt {(\ Delta x) ^ 2 + (\ Delta y) ^ 2} = \ sqrt {(x_2-x_1) ^ 2 + (Y_2-y_1) ^ 2}. \,$

Le secteur m??me, donn??s (x _1, y _1, z ₁₎ et (x _2, y _2, z ₂₎ dans l'espace tridimensionnel , la distance entre eux est

$d = \ sqrt {(\ Delta x) ^ 2 + (\ Delta y) ^ 2 + (\ Delta z) ^ 2} = \ sqrt {(x_1-x_2) ^ 2 + (y_1-Y_2) ^ 2 + ( z_1-Z_2) ^ 2}.$

Qui est facilement prouv?? par la construction d'un triangle rectangle avec une jambe sur le hypot??nuse d'un autre (avec l'autre jambe orthogonal au plan contenant le premier triangle) et en appliquant le th??or??me de Pythagore .

Dans l'??tude de g??om??tries complexes, nous appelons ce type (le plus courant) de la distance Distance euclidienne, comme il est d??riv?? du th??or??me de Pythagore , qui ne tient pas en G??om??tries non-euclidiennes. Cette distance formule peut ??galement ??tre ??tendu dans le formule longueur d'arc.

Distance dans l'espace euclidien

Dans l' espace euclidien R ^n, la distance entre deux points est g??n??ralement donn?? par la Distance euclidienne (?? distance 2-norme). Autres distances, fond??es sur d'autres normes, sont parfois utilis??s ?? la place.

Pour un point (x _1, x _2, ..., x _n) et un point (y _1, y _2, ..., y _n), la distance de Minkowski d'ordre p (distance p-norme) est d??finie comme :

La distance norme 1	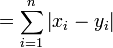$= \ Sum_ {i = 1} ^ n \ left \| x_i - y_i \ right \|$
La distance norme 2	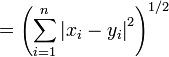$= \ Left (\ sum_ {i = 1} ^ n \ left \| x_i - y_i \ right \| ^ 2 \ right) ^ {1/2}$
p -norme la distance	$= \ Left (\ sum_ {i = 1} ^ n \ left \| x_i - y_i \ right \| ^ p \ right) ^ {1 / p}$
norme infinie la distance	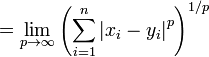$= \ Lim_ {p \ to \ infty} \ left (\ sum_ {i = 1} ^ n \ left \| x_i - y_i \ right \| ^ p \ right) ^ {1 / p}$
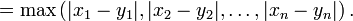	$= \ Max \ gauche (\| x_1 - y_1 \|, \| x_2 - Y_2 \|, \ ldots, \| x_n - y_n \| \ right).$

p ne est pas n??cessairement un nombre entier, mais il ne peut pas ??tre inf??rieur ?? 1, car sinon le in??galit?? triangulaire ne tient pas.

La distance 2-norme est la Distance euclidienne, une g??n??ralisation du th??or??me de Pythagore ?? plus de deux coordonne. Ce est ce que l'on obtiendrait si la distance entre deux points ont ??t?? mesur??s avec un r??gle: l'id??e ??intuitive?? de la distance.

La distance norme 1 est plus imag??e appel?? la norme de taxi ou Distance de Manhattan, parce que ce est la distance d'une voiture serait conduire dans une ville am??nag?? dans des blocs carr??s (se il n'y a pas de rues ?? sens unique).

La distance de l'infini norme est aussi appel?? La distance Chebyshev. En 2D repr??sente la distance rois doivent voyager entre deux carr??s sur un ??chiquier.

Le p -norme est rarement utilis?? pour des valeurs de p autres que 1, 2, et l'infini, mais voir super-ellipse.

Dans l'espace physique de la distance euclidienne est d'une mani??re la plus naturelle, car dans ce cas la longueur d'un corps rigide ne change pas avec rotation.

Cas g??n??ral

En math??matiques , en particulier la g??om??trie , une fonction de distance sur une donn??e M est d??fini une fonction d: M ?? M → R, o?? R est l'ensemble des nombres r??els , qui satisfait aux conditions suivantes:

d (x, y) ≥ 0, et d (x, y) = 0 si et seulement si x = y. (Distance est positive entre deux points diff??rents, et est nul pr??cis??ment d'un point ?? lui-m??me.)
C'est sym??trique: d (x, y) = d (y, x). (La distance entre x et y est la m??me dans les deux sens).
Il r??pond ?? la triangle in??galit??: d (x, z) ≤ d (x, y) + d (y, z). (La distance entre deux points est la plus courte distance le long d'une voie).

Une telle fonction de la distance est connue en tant que m??trique. Avec l'ensemble, il fait un espace m??trique.

Par exemple, la d??finition usuelle de la distance entre deux nombres r??els x et y est: d (x, y) = | x - y |. Cette d??finition satisfait aux trois conditions ci-dessus, et correspond ?? la norme topologie du ligne r??elle. Mais la distance sur un ensemble donn?? est un choix de d??finition. Un autre choix possible consiste ?? d??finir: d (x, y) = 0 si x = y, et 1 sinon. Ce d??finit ??galement une m??trique, mais donne une topologie compl??tement diff??rent, le " topologie discr??te ", avec ce nombre de d??finition ne peut ??tre arbitrairement proche.

Les distances entre les ensembles et entre un point et un ensemble

d (A, B)> d (A, C) + d (C, B)

Diverses d??finitions de distance sont possibles entre les objets. Par exemple, entre les corps c??lestes ne faut pas confondre la distance surface-surface et la distance de centre ?? centre. Dans le premier cas est tr??s inf??rieure ?? celle-ci, comme pour un LEO, la premi??re tend ?? ??tre cit?? (altitude), sinon, par exemple pour la distance Terre-Lune, ce dernier.

Il ya deux d??finitions communes pour la distance entre deux non vides sous-ensembles d'un ensemble donn??:

Une version de la distance entre deux ensembles non vides est le infimum des distances entre deux de leurs points respectifs, ce qui est la signification de tous les jours de la parole. Ce est un sym??trique prametric. Sur une collection d'ensembles dont certains tactile ou se chevauchent, il ne est pas "s??paration", parce que la distance entre deux ensembles diff??rents mais touchant ou se chevauchant est z??ro. En outre, il ne est pas hemimetric, ?? savoir la in??galit?? triangulaire ne tient pas, sauf dans des cas particuliers. Par cons??quent seulement dans des cas particuliers cette distance permet une collection d'ensembles d'un espace m??trique.
Le Distance de Hausdorff est la plus grande des deux valeurs, l'une ??tant la borne sup??rieure, pour un point allant sur un ensemble, de la borne inf??rieure, pour un deuxi??me point allant sur l'autre ensemble, de la distance entre les points, et l'autre valeur ??tant ??galement d??fini mais avec les r??les des deux ensembles ??chang??s. Cette distance fait l'ensemble des non-vides compacts sous-ensembles d'un espace m??trique elle-m??me un espace m??trique.

Le Module: Metric_space ( parler ?? ?? hist ?? ?? liens ?? sous-pages essais - r??sultats) est la borne inf??rieure des distances entre le point et celles de l'ensemble. Cela correspond ?? la distance, selon la d??finition mentionn??e en premier lieu ci-dessus pour la distance entre les ensembles, de l'ensemble contenant seulement ce point ?? l'autre ensemble.

En termes de cela, la d??finition de la distance de Hausdorff peut ??tre simplifi??e: ce est la plus grande des deux valeurs, l'une ??tant la borne sup??rieure, pour un point allant sur un ensemble, de la distance entre le point et le jeu, et l'autre valeur ??tant ??galement d??fini mais avec les r??les des deux ensembles ??chang??s.

Distance en fonction du d??placement

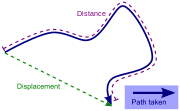
Distance long d'un chemin par rapport au d??placement

Distance ne peut pas ??tre n??gative . La distance est une quantit?? scalaire, contenant seulement grandeur, tandis que d??placement est un ??quivalent vecteur quantit?? contenant ?? la fois l'ampleur et direction.

La distance parcourue par un v??hicule (souvent enregistr?? par un odom??tre), personne, un animal, un objet, etc. doit ??tre distingu??e de la distance entre le point de d??part jusqu'au point final, m??me si ce dernier est pris pour signifier par exemple la plus courte distance le long de la route, car un d??tour pourrait ??tre faite, et le point final peut m??me co??ncider avec le point de d??part.

Autres "distances"

La distance de Mahalanobis est utilis??e dans les statistiques .
La distance de Hamming est utilis?? dans th??orie du codage.
Levenshtein
Distance de Tchebychev

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Distance&oldid=202869167 "

La distance norme 1	$= \ Sum_ {i = 1} ^ n \ left \| x_i - y_i \ right \|$
La distance norme 2	$= \ Left (\ sum_ {i = 1} ^ n \ left \| x_i - y_i \ right \| ^ 2 \ right) ^ {1/2}$
p -norme la distance	$= \ Left (\ sum_ {i = 1} ^ n \ left \| x_i - y_i \ right \| ^ p \ right) ^ {1 / p}$
norme infinie la distance	$= \ Lim_ {p \ to \ infty} \ left (\ sum_ {i = 1} ^ n \ left \| x_i - y_i \ right \| ^ p \ right) ^ {1 / p}$
	$= \ Max \ gauche (\| x_1 - y_1 \|, \| x_2 - Y_2 \|, \ ldots, \| x_n - y_n \| \ right).$