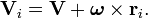Vitesse angulaire
Renseignements g??n??raux
SOS croit que l'??ducation donne une meilleure chance dans la vie des enfants dans le monde en d??veloppement aussi. SOS Enfants a regard?? des enfants en Afrique depuis quarante ans. Pouvez-vous aider dans leur travail en Afrique ?
- Ne pas confondre avec fr??quence angulaire

Dans la physique , de la vitesse angulaire est un vecteur quantit?? (plus pr??cis??ment, un pseudovector) qui pr??cise les la vitesse angulaire ?? laquelle un objet est en rotation avec la direction dans laquelle il tourne. Le Unit?? de mesure de vitesse angulaire est radians par seconde, m??me si elle peut ??tre mesur??e dans d'autres unit??s telles que degr??s par seconde, degr??s par heure, etc. Lorsque mesur??e en cycles ou rotations par unit?? de temps (par exemple, tours par minute), il est souvent appel?? la vitesse de rotation et de son ampleur la vitesse de rotation. La vitesse angulaire est g??n??ralement repr??sent?? par le symbole om??ga (Ω ou ω). La direction du vecteur de vitesse angulaire est perpendiculaire au plan de rotation, dans une direction qui est g??n??ralement indiqu?? par le r??gle de la main droite.
La vitesse angulaire d'une particule
Deux dimensions

La vitesse angulaire d'une particule dans un plan deux dimensions est la plus facile ?? comprendre. Comme le montre la figure de droite (exprimant g??n??ralement les mesures angulaires φ et θ en radians ), si nous tra??ons une ligne ?? partir de l'origine (O) ?? la particule (P), alors le vecteur de vitesse ( 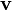 ) De la particule aura une composante le long du rayon (
) De la particule aura une composante le long du rayon ( 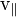 - La composante radiale) et une composante perpendiculaire au rayon (
- La composante radiale) et une composante perpendiculaire au rayon ( 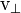 - La composante tangentielle).
- La composante tangentielle).
Un mouvement radial ne produit pas de rotation de la particule (par rapport ?? l'origine), de sorte ?? des fins de recherche de la vitesse angulaire de la parall??le (radiale) composant peut ??tre ignor??. Par cons??quent, la rotation est totalement produite par le mouvement tangentiel (comme celle d'une particule se d??pla??ant le long d'une circonf??rence), et la vitesse angulaire est compl??tement d??termin??e par la (tangentiel) composante perpendiculaire.
On peut voir que le taux de variation de la position angulaire de la particule est li??e ?? la vitesse tangentielle par:
En utilisant θ, l'angle entre les vecteurs 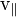 et v, ou de mani??re ??quivalente comme ??tant l'angle entre les vecteurs r et v, on obtient:
et v, ou de mani??re ??quivalente comme ??tant l'angle entre les vecteurs r et v, on obtient:
En combinant les deux ??quations ci-dessus et de d??finir la vitesse angulaire ω, les rendements = & phiv / dt:
En deux dimensions la vitesse angulaire est un num??ro unique qui n'a pas de sens. Un seul num??ro qui n'a pas de direction est soit un ou un scalaire pseudoscalaire, la diff??rence ??tant que un scalaire ne change pas son signe quand les axes x et y sont ??chang??s (ou invers??), tandis qu'un pseudoscalaire fait. L'angle ainsi que la vitesse angulaire est un pseudoscalaire. Le sens de rotation positif est repris, par convention, pour ??tre dans la direction de l'axe y de l'axe x. Si les axes sont invers??s, mais le sens de rotation ne est pas, alors le signe de l'angle de rotation, et donc la vitesse angulaire ainsi, va changer.
Il est important de noter que la vitesse angulaire pseudoscalaire d'une particule d??pend du choix de l'origine et de l'orientation des axes de coordonn??es.
Trois dimensions
En trois dimensions, la vitesse angulaire devient un peu plus compliqu??. La vitesse angulaire dans ce cas est g??n??ralement consid??r?? comme un vecteur , ou plus pr??cis??ment, un pseudovector. Il a maintenant non seulement une grandeur, mais une direction ainsi. L'ampleur est la vitesse angulaire et la direction d??crit la axe de rotation. Le r??gle de la main droite indique le sens positif de la pseudovector de vitesse angulaire, ?? savoir:
- Si vous courbez les doigts de votre main droite pour suivre la direction de la rotation, puis la direction du vecteur de vitesse angulaire est indiqu?? par votre pouce droit.
Tout comme dans le cas ?? deux dimensions, une particule aura une composante de sa vitesse le long du rayon de l'origine de la particule, et une autre composante perpendiculaire ?? ce rayon. La combinaison du point de d??part et de la composante perpendiculaire de la vitesse d??finit un plan de rotation dans lequel le comportement de la particule (pour l'instant) appara??t comme il le fait dans le cas bidimensionnel. L'axe de rotation est alors une ligne perpendiculaire ?? ce plan, et cet axe d??fini le sens de la pseudo-vecteur de vitesse angulaire, tandis que l'amplitude est la m??me que la valeur pseudoscalaire trouv?? dans le cas deux dimensions. D??finir un vecteur unitaire 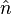 qui pointe dans la direction de l'pseudovector de vitesse angulaire. La vitesse angulaire peut ??tre ??crit d'une mani??re similaire ?? celle de deux dimensions:
qui pointe dans la direction de l'pseudovector de vitesse angulaire. La vitesse angulaire peut ??tre ??crit d'une mani??re similaire ?? celle de deux dimensions:
qui, par la d??finition du produit vectoriel , peut se ??crire:
Dimensions sup??rieures
En g??n??ral, la vitesse angulaire dans un espace ?? n dimensions est la d??riv??e de temps du d??placement angulaire tenseur qui est un deuxi??me rang antisym??trique tenseur. Ce tenseur devra n (n-1) / 2 composantes ind??pendantes et ce nombre est la dimension de la Alg??bre de Lie du groupe de Lie des rotations d'un espace de produit interne de dimension n. Il se av??re que dans un espace tridimensionnel vitesse angulaire peut ??tre repr??sent?? par le vecteur, car le nombre de composantes ind??pendantes est ??gale ?? nombre de dimensions de l'espace.
Vitesse d'un corps rigide angulaire
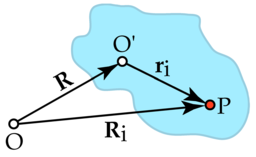
Afin de traiter avec le mouvement d'un corps rigide, il est pr??f??rable d'envisager un syst??me qui est fixe par rapport au corps rigide coordonn??e, et d'??tudier les transformations de coordonn??es entre cette coordonn??e et le syst??me fixe "de laboratoire". Comme le montre la figure de droite, l'origine du syst??me de laboratoire est au point O, l'origine du syst??me de corps rigide est ?? O 'et le vecteur de O ?? O' est R. Une particule (i) dans le corps rigide est situ?? au point P et le vecteur de position de cette particule est R i dans la trame de laboratoire, et ?? la position r i dans la trame de corps. On voit que la position de la particule peut se ??crire:
La caract??ristique d'un corps rigide est que la distance entre deux points quelconques dans un corps rigide est invariable dans le temps. Cela signifie que la longueur du vecteur  est immuable. Par P??le eul??rien, nous peut remplacer le vecteur
est immuable. Par P??le eul??rien, nous peut remplacer le vecteur  avec
avec 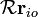 o??
o?? 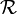 est un matrice de rotation et
est un matrice de rotation et 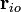 est la position de la particule ?? un point fixe dans le temps, dire t = 0. Ce remplacement est utile, parce que maintenant ce ne est que la matrice de rotation
est la position de la particule ?? un point fixe dans le temps, dire t = 0. Ce remplacement est utile, parce que maintenant ce ne est que la matrice de rotation 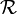 qui ??volue dans le temps et non pas le vecteur de r??f??rence
qui ??volue dans le temps et non pas le vecteur de r??f??rence 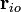 , Que le corps rigide tourne autour du point O '. La position de la particule est maintenant ??crire:
, Que le corps rigide tourne autour du point O '. La position de la particule est maintenant ??crire:
En prenant la d??riv??e de temps donne le vitesse de la particule:
o?? V i est la vitesse de la particule (dans le cadre du laboratoire) et v est la vitesse de O '(l'origine du cadre de corps rigide). Depuis 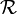 est une matrice de rotation inverse de sa sa sa transpos??e. Donc, nous substituons
est une matrice de rotation inverse de sa sa sa transpos??e. Donc, nous substituons 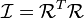 :
:
Continuer en prenant le temps de derivitve 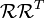 :
:
En appliquant la formule (AB) T = B T A T:
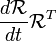 est le n??gatif de sa transpos??e. Il est donc une matrice 3x3 antisym??trique. Nous pouvons donc prendre sa double pour obtenir un vecteur en 3 dimensions.
est le n??gatif de sa transpos??e. Il est donc une matrice 3x3 antisym??trique. Nous pouvons donc prendre sa double pour obtenir un vecteur en 3 dimensions. 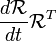 est appel?? le tenseur de vitesse angulaire . Si nous prenons le double de ce tenseur, la multiplication de matrices est remplac?? par le produit crois??. Son double est appel?? le pseudovector de vitesse angulaire, ω.
est appel?? le tenseur de vitesse angulaire . Si nous prenons le double de ce tenseur, la multiplication de matrices est remplac?? par le produit crois??. Son double est appel?? le pseudovector de vitesse angulaire, ω.
En substituant ω dans l'expression de vitesse ci-dessus:
On peut voir que la vitesse d'un point dans un corps rigide peut ??tre divis?? en deux termes - la vitesse d'un point fixe dans le corps rigide, plus la dur??e transversale du produit impliquant la vitesse angulaire de la particule par rapport au point de r??f??rence r??f??rence . Cette vitesse angulaire est le "spin" vitesse angulaire du corps rigide par rapport ?? la vitesse angulaire du point de r??f??rence O 'sur l'origine O.
Ce est un point important que la vitesse angulaire de rotation de chaque particule dans le corps rigide est la m??me, et que la vitesse angulaire de rotation est ind??pendant du choix de l'origine du syst??me de corps rigide ou du syst??me de laboratoire. En d'autres termes, ce est une quantit?? physique r??elle, qui est une propri??t?? du corps rigide, ind??pendant de son choix de syst??me de coordonn??es. La vitesse angulaire du point sur l'origine de la volont?? de trame de laboratoire de r??f??rence, cependant, d??pendent de ces choix de syst??me de coordonn??es. Il est souvent commode de choisir le centre de masse du corps rigide que l'origine du syst??me de corps rigide, depuis une simplification consid??rable se produit math??matique dans l'expression de la vitesse angulaire du corps rigide.

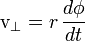
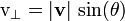
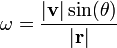
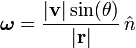
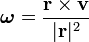
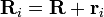
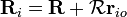
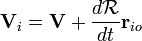
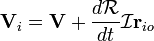
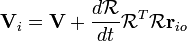
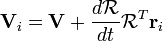
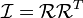
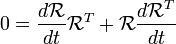
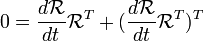
![\ Boldsymbol \ omega = [\ omega_x, \ omega_y, \ omega_z]](../../images/147/14774.png)