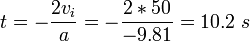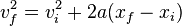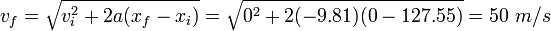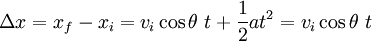Cin??matique

Renseignements g??n??raux

SOS Enfants a fait cette s??lection Wikipedia aux c??t??s d'autres ??coles des ressources . Cliquez ici pour plus d'informations sur les enfants SOS.

Cin??matique ( grec κινειν, kinein, se d??placer) est une branche de la dynamique qui d??crit le mouvement d'objets sans la prise en compte des masses ou des forces qui font ressortir le mouvement. En revanche, cin??tique est concern?? avec les forces et interactions qui produisent ou qui affectent le mouvement.

L'application la plus simple de la cin??matique est de montrer le mouvement des particules ( cin??matique cin??matique de translation ou lin??aire). La description de rotation ( la cin??matique de rotation ou angulaires cin??matique) est plus compliqu??. L'??tat d'un corps rigide g??n??rique peut ??tre d??crit en combinant ?? la fois la traduction et la cin??matique de rotation ( la cin??matique de corps rigide). Un cas plus compliqu?? est la cin??matique d'un syst??me de corps rigides, ??ventuellement reli??s entre eux par des moyens m??caniques articulations. La description cin??matique de l'??coulement du fluide est encore plus compliqu??, et pas g??n??ralement consid??r?? dans le contexte de la cin??matique.

Translation

Translationnelle ou cin??matique curvilignes est la description du mouvement dans l'espace d'un point le long d'une trajectoire. Ce chemin peut ??tre lin??aire ou courbe comme on le voit avec le mouvement du projectile. Il ya trois concepts de base qui sont n??cessaires pour comprendre le mouvement de translation:

Le d??placement est la distance la plus courte entre deux points: l'origine et le point d??plac??es. L'origine est (0,0) sur une syst??me qui est d??fini par l'observateur de coordonn??es. Parce que le d??placement a ?? la fois l'ampleur (longueur) et la direction, ce est un vecteur dont le point de d??part est l'origine et le point terminal est le point d??plac??.
La vitesse est la vitesse de variation de d??placement en fonction du temps; ce est le d??placement d'un point change avec le temps. Velocity est ??galement un vecteur. Pour une vitesse constante, chaque unit?? de temps ajoute la longueur du vecteur vitesse (dans le m??me sens) pour le d??placement de la pointe mobile. Vitesse instantan??e (la vitesse ?? un instant de temps) est d??finie comme 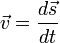$\ Vec v = \ frac {d \ vec s} {d} t$ , O?? ds est un infiniment petit d??placement et dt est un infiniment petit laps de temps. La vitesse moyenne (vitesse sur une longueur de temps) est d??finie comme 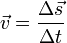$\ Vec v = \ frac {\ Delta \ vec s} {\ Delta t}$ O?? Δs est le changement dans le d??placement et At est l'intervalle de temps pendant laquelle le d??placement changements.
L'acc??l??ration est la vitesse de variation de la vitesse par rapport au temps. L'acc??l??ration est ??galement un vecteur. Comme avec une vitesse si l'acc??l??ration est constante, pour chaque unit?? de temps de la longueur du vecteur d'acc??l??ration (dans le m??me sens) est ajout??e ?? la vitesse. Si la variation de la vitesse (un vecteur) est connu, l'acc??l??ration est parall??le. Acc??l??ration instantan??e (l'acc??l??ration ?? un instant de temps) est d??finie comme $\ Vec a = \ frac {d \ vec v} {d} t$ O?? dv est un infiniment petit changement de vitesse et dt est un infiniment petit laps de temps. 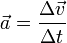Acc??l??ration moyenne (d'acc??l??ration sur une longueur de temps) est d??finie comme $\ Vec a = \ frac {\ Delta \ vec v} {\ Delta t}$ O?? Av est le changement de vitesse et At est l'intervalle de temps pendant lequel les changements de vitesse.

Lorsque l'acc??l??ration est constante, il est dit ??tre en cours de mouvement uniform??ment acc??l??r??. Si tel est le cas, il ya quatre ??quations qui peuvent ??tre utilis??s pour d??crire le mouvement d'un objet.

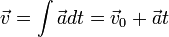$\ Vec v = \ int \ vec une dt = \ vec v_0 + \ vec un t$ Ceux qui sont familiers avec le calcul peut reconna??tre comme un probl??me de valeur initiale. ??tant donn?? que l'acc??l??ration (a) est une constante, int??grant par rapport au temps (t) donne un changement de vitesse. L'ajout de ce ?? la vitesse initiale (v ₀₎ donne la vitesse finale (V).
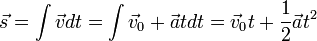$\ Vec s = \ int \ vec v dt = \ int \ v_0 vec + \ vec au dt = \ vec v_0 t + \ frac {1} {2} \ vec au ^ 2$ En utilisant la formule ci-dessus, nous pouvons substituer ?? v pour arriver ?? cette ??quation, o?? s est le d??placement.
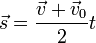$\ = \ Frac de l'vec {\ vec v + \ vec v_0} {2} t$ En utilisant la d??finition d'un moyenne, et la connaissance que les temps de la vitesse moyenne du temps de d??placement est ??gal, nous pouvons arriver ?? cette ??quation.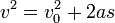
$v ^ 2 = v_0 ^ 2 + 2 une s$

Vitesse relative

Pour d??crire le mouvement de l'objet A par rapport ?? l'objet O, quand on sait comment chacun se d??place par rapport ?? l'objet B, nous utilisons l'??quation suivante impliquant des vecteurs et addition de vecteurs:

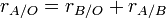
$r_ {A / S} = {r_ B / O} + r_ {A / B} \, \!$

L'??quation de mouvement relatif ci-dessus indique que le mouvement de A par rapport ?? O est ??gale ?? la motion de B par rapport ?? O, plus le mouvement de A par rapport ?? B.

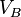Par exemple, laissez-Ann se d??placer avec vitesse $V_ {A}$ et laissez Bob d??placer avec une vitesse $V_ {B}$ , Chaque vitesse donn??e par rapport au sol. Pour trouver quelle vitesse Ann se d??place par rapport ?? Bob (nous appelons cette vitesse 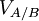$V_ {A / B}$ ), L'??quation ci-dessus donne:

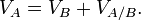
$V_ {A} = V_ {B} + V_ {A / B} \, \! .$

Trouver 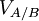$V_ {A / B}$ nous r??organisons tout simplement cette ??quation pour obtenir:

$V_ {A / B} = V_ {A} -V_ {B} \, \! .$

A des vitesses comparables ?? la vitesse de la lumi??re , ces ??quations sont pas valides. Ils sont remplac??s par des ??quations d'Einstein d??riv??s de la th??orie de la relativit?? restreinte .

Exemple: rectiligne (1D) mouvement

Un objet est tir?? vers le haut, atteint son sommet, puis commence sa descente dans une acc??l??ration constante.

Consid??rons un objet qui est tir?? directement vers le haut et retombe sur le sol de sorte que sa trajectoire est contenue dans une ligne droite. Si nous adoptons la convention que la direction vers le haut est le sens positif, l'objet subit une acc??l??ration constante d'environ -9,81 m / s ^2. Par cons??quent, son mouvement peut ??tre mod??lis??e avec les ??quations r??gissant mouvement uniform??ment acc??l??r??.

Par souci d'exemple, supposons que l'objet a une vitesse initiale de 50 m / s. Il ya plusieurs questions cin??matiques int??ressantes que nous pouvons poser au sujet de la motion de la particule:

Combien de temps faudra-il l'air?

Pour r??pondre ?? cette question, nous appliquons la formule

$x_f - x_i = v_i t + \ frac {1} {2} au ^ 2.$

Puisque la question demande la longueur de temps entre l'objet quitter le sol et frapper le sol sur sa chute, le d??placement est z??ro.

$0 = v_i t + \ frac {1} {2} au ^ 2 = t (v_i + \ frac {1} {2} at)$

Nous trouvons deux solutions pour cela. La solution triviale affirme que le temps est z??ro; ce est effectivement vrai aussi, ce est le premier moment le d??placement est nul: juste au moment o?? il amorce le mouvement. Toutefois, la solution est d'int??r??t

$t = - \ frac {} 2v_i {a} = - \ frac {2} {* 50 - 9,81 = 10,2} \ s$

Que faut-il atteindre l'altitude avant qu'il ne commence ?? tomber?

Dans ce cas, on utilise le fait que l'objet a une vitesse de z??ro au sommet de sa trajectoire. Par cons??quent, l'??quation est applicable:

$v_F ^ 2 = v_i ^ 2 + 2 bis (x_f - x_i)$

Si l'origine de notre syst??me de coordonn??es est au sol, puis 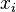$x_i$ est z??ro. Puis nous r??solvons pour 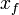$x_f$ et substitut valeurs connues:

$x_f = \ frac {v_F ^ 2 - v_i ^ 2} {2} + un x_i = \ frac {0-50 ^ 2} {2} * -9,81 0 = 127,55 \ m$

Quelle sera sa vitesse finale ??tre quand il atteint le sol?

Pour r??pondre ?? cette question, nous utilisons le fait que l'objet a une vitesse initiale de z??ro au sommet avant qu'il ne commence sa descente. Nous pouvons utiliser la m??me ??quation que nous avons utilis?? pour la derni??re question, en utilisant la valeur de 127,55 m pour $x_i$ .

$v_F = \ sqrt {v_i ^ 2 + 2 bis (x_f - x_i)} = \ sqrt {0 ^ 2 + 2 (-9,81) (0 ?? 127,55)} = 50 \ m / s$

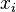En supposant que cette exp??rience a ??t?? r??alis??e sous vide (niant les effets de tra??n??e), nous constatons que les vitesses finales et initiales sont ??gales, un r??sultat qui est d'accord avec conservation de l'??nergie.

Exemple: Projectile (2D) mouvement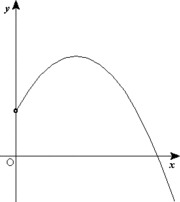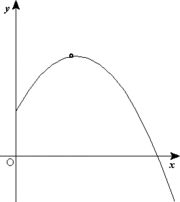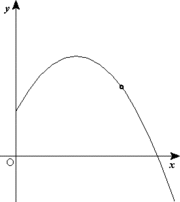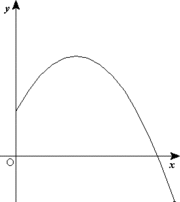

Un objet tir?? ?? un angle $\ Theta$ ?? partir du sol suit une trajectoire parabolique.

Supposons qu'un objet ne est pas tir?? verticalement, mais est tir?? ?? un angle $\ Theta$ ?? partir du sol. L'objet sera alors suivre une trajectoire parabolique, et son mouvement horizontal peut ??tre mod??lis?? ind??pendamment de son mouvement vertical. On suppose que l'objet est cuit ?? une vitesse initiale de 50 m / s et 30 degr??s par rapport ?? l'horizontale.

Jusqu'o?? faut-il voyager avant de toucher le sol?

L'objet subit une acc??l??ration de -9,81 ms ^-2 dans la direction verticale et pas d'acc??l??ration dans la direction horizontale. Par cons??quent, le d??placement horizontal est

$\ Delta x = x_f - x_i = v_i \ cos \ theta \ t + \ frac {1} {2} au ^ 2 = v_i \ cos \ theta \ t$

Pour r??soudre cette ??quation, nous devons trouver t. Cela peut ??tre fait en analysant le mouvement dans la direction verticale. Si nous imposons que le d??placement vertical est ??gal ?? z??ro, nous pouvons utiliser la m??me proc??dure que nous avons fait pour le mouvement rectiligne de trouver t.

$0 = v_i \ sin \ theta \ t + \ frac {1} {2} au ^ 2 = t (v_i \ sin \ theta + \ frac {1} {2} at)$

Nous r??solvons maintenant t et rempla??ons cette expression dans l'expression original pour d??placement horizontal. (Notez l'utilisation de la identit?? trigonom??trique $2 \ sin \ theta \ cos \ theta = \ sin 2 \ theta$ )

$\ Delta x = v_i \ cos \ theta \ left (\ frac {-2 v_i \ sin \ theta} {a} \ right) = - \ frac {v_i ^ 2 \ sin 2 \ theta} {a} = 220,93 \ m$

Un mouvement de rotation

Le vecteur de vitesse angulaire pointe vers le haut pour la rotation dans le sens antihoraire et vers le bas pour une rotation dans le sens horaire, comme sp??cifi?? par le R??gle de la main droite.

La cin??matique de rotation est la description de la rotation d'un objet et implique la d??finition et l'utilisation des trois quantit??s suivantes:

Position angulaire: Si un vecteur est d??fini comme ??tant la distance orient??e de l'axe de rotation jusqu'?? un point sur un objet, la position angulaire de ce point est l'angle orient?? $\ Theta$ ?? partir d'un axe de r??f??rence (par exemple, les x-de demi-axe positifs) ?? ce vecteur. Un angle est un angle orient?? balay?? autour d'un axe de rotation connue et dans un sens de rotation connue. Dans la cin??matique en deux dimensions (la description du mouvement planaire), l'axe de rotation est normale au cadre de r??f??rence et peuvent ??tre repr??sent??s par un point de rotation (ou centre), et le sens de rotation est repr??sent?? par le signe de l'angle (g??n??ralement, un signe positif signifie sens antihoraire). D??placement angulaire peut ??tre consid??r?? comme une position relative. Elle est repr??sent??e par l'angle orient?? balay??e par le point mentionn?? ci-dessus (ou vecteur), d'une position angulaire ?? l'autre.

Vitesse angulaire: la grandeur de la vitesse angulaire 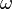$\ Omega$ est la vitesse ?? laquelle la position angulaire $\ Theta$ des changements par rapport au temps t:

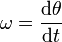
$\ Mathbf {\ omega} = \ frac {\ mathrm {d} \ theta} {\ mathrm {d} t}$

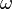Acc??l??ration angulaire: L'amplitude de l'acc??l??ration angulaire $\ Alpha$ est la vitesse ?? laquelle la vitesse angulaire $\ Omega$ des changements par rapport au temps t:

$\ Mathbf {\ alpha} = \ frac {\ mathrm {d} \ mathbf {\ omega}} {\ mathrm {d} t}$

Les ??quations de la cin??matique de translation peuvent facilement ??tre ??tendues ?? la cin??matique de rotation plane avec ??changes variables simples:

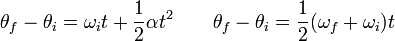
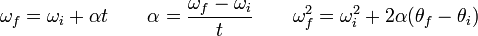
$\ \ \ Theta_f -! \ Theta_i = \ omega_i t + \ frac {1} {2} \ alpha t ^ 2 \ qquad \ theta_f - \ theta_i = \ frac {1} {2} (\ + omega_f \ omega_i) t$ $! \, \ \ Omega_f = \ omega_i + \ alpha t \ qquad \ alpha = \ frac {\ omega_f - \ omega_i} {t} \ qquad \ omega_f ^ 2 = \ omega_i ^ 2 + 2 \ alpha (\ theta_f - \ theta_i)$

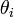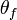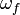Ici $\, \! \ Theta_i$ et $\, \! \ Theta_f$ sont, respectivement, les positions angulaires initiales et finales, $\, \! \ Omega_i$ et $\, \! \ Omega_f$ sont, respectivement, les vitesses angulaires initiales et finales, et $\, \! \ Alpha$ est l'acc??l??ration angulaire constante. Bien que la position dans l'espace et de la vitesse dans l'espace sont deux vecteurs de mouvement vrai (en termes de leurs propri??t??s dans la rotation), comme ce est la vitesse angulaire, angle soi ne est pas un v??ritable vecteur.

Syst??mes de coordonn??es

Dans une situation donn??e, coordonn??es les plus utiles peuvent ??tre d??termin??es par contraintes sur le mouvement ou par la nature g??om??trique de la force provoquant ou affectant la motion. Ainsi, pour d??crire le mouvement d'une bille contraint de se d??placer le long d'un arceau circulaire dont le plus utile de coordonn??es peut ??tre son angle sur la frette. De m??me, pour d??crire le mouvement d'une particule charg??e par un force centrale, coordonn??es les plus utiles peuvent ??tre coordonn??es polaires .

Coordonn??es rectangulaires fixes

Dans ce syst??me de coordonn??es, les vecteurs sont exprim??s comme une addition de vecteurs dans le plan x, y, et z direction ?? partir d'une origine non tournante. Habituellement i est un vecteur unitaire dans la direction x, j est un vecteur unitaire dans la direction y, et k est un vecteur unitaire dans la direction z.

Le vecteur de position, S (ou R), le vecteur de vitesse, v, et l' acc??l??ration vecteur, sont exprim??s en utilisant des coordonn??es rectangulaires de la mani??re suivante:

$\ S vec = x \ vec i + Y j vec \ + z \ vec k \, \!$

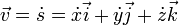
$\ Vec v = \ dot {s} = \ dot {x} \ vec {i} + \ dot {y} \ vec {j} + \ dot {z} \ vec {k} \, \!$

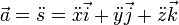
$\ Vec a = \ ddot {s} = \ ddot {x} \ vec {i} + \ ddot {y} \ vec {j} + \ {z ddot} \ vec {k} \, \!$

Remarque: 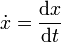$\ Dot {x} = \ frac {\ mathrm {d} x} {\ mathrm {d} t}$ , $\ Ddot {x} = \ frac {\ mathrm {d} ^ 2x} {\ mathrm {d} t ^ 2}$

Trois rotation dimensions cadre de coordonn??es

(?? ??crire)

Contraintes cin??matiques

Une contrainte cin??matique est toute condition relative propri??t??s d'un syst??me dynamique qui doit ??tre vrai en tout temps. Voici quelques exemples courants:

Rouler sans glisser

Un objet qui roule contre un surface sans glisser ob??it ?? la condition que la vitesse de son centre de masse est ??gal au produit vectoriel de la vitesse angulaire d'un vecteur ?? partir du point de contact au centre de masse,:

$v_G (t) {G / O de l'} = \ omega de \ times \, \!$

Pour le cas d'un objet qui ne est pas basculer ou tourner, ce qui r??duit ?? v = R ω.

Cordon inextensible

Ce est le cas o?? les corps sont reli??s par un cordon qui reste en tension et ne peut pas changer de longueur. La contrainte est que la somme de tous les composants de la moelle, mais ils sont d??finis, est la longueur totale, et la d??riv??e temporelle de cette somme est nulle.

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Kinematics&oldid=199418384 "