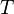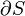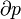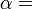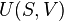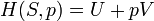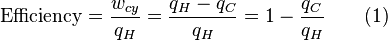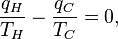Temp??rature thermodynamique
Contexte des ??coles Wikip??dia
SOS Enfants a fait cette s??lection Wikipedia aux c??t??s d'autres ??coles des ressources . Cliquez ici pour plus d'informations sur les enfants SOS.
| Thermodynamique | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 Le classique Cycle de Carnot. | |||||||||||||||||||||
Branches
| |||||||||||||||||||||
Lois
| |||||||||||||||||||||
Syst??mes ??tat
Processus
Cycles
| |||||||||||||||||||||
Propri??t??s syst??me
Fonctions d'Etat ( Variables conjugu??es en italique)
| |||||||||||||||||||||
Propri??t??s des mat??riaux
Click on the following link to visit or download this HTML page
| |||||||||||||||||||||
??quations
| |||||||||||||||||||||
Potentiels
| |||||||||||||||||||||
Philosophie
Histoire
Th??ories
Principales publications
??ch??ancier
Art
??ducation
| |||||||||||||||||||||
Les scientifiques
| |||||||||||||||||||||
Temp??rature thermodynamique est la mesure absolue de la temp??rature et il est l'un des principaux param??tres de la thermodynamique .
Temp??rature thermodynamique est une "absolue" ??chelle parce que ce est la mesure de la propri??t?? fondamentale sous-jacente temp??rature: son nul ou z??ro, z??ro absolu , est la temp??rature ?? laquelle les constituants des particules de la mati??re ont mouvement minime et peuvent devenir pas plus froid.
?? son plus simple, la temp??rature provient de l' ??nergie cin??tique des mouvements vibratoires de mati??re de mandants de particules ( mol??cules , atomes , et particules subatomiques). La vari??t?? compl??te de ces motions cin??tiques, avec ??nergies potentielles de particules, et aussi parfois certains autres types d'??nergie de particules en ??quilibre avec ceux-ci, contribuent total l'??nergie interne dans une substance. L'??nergie interne est vaguement appel?? la chaleur ou l'??nergie l'??nergie thermique dans des conditions en l'absence de travail est r??alis?? sur le fond de son environnement, ou par la substance sur l'environnement. L'??nergie interne peut ??tre stock??e dans un certain nombre de fa??ons dans une substance, mais seulement l'??nergie cin??tique des particules contribue ?? la temp??rature de la substance.
Vue d'ensemble
Temp??rature r??sulte des vibrations al??atoires submicroscopiques des constituants de particules de mati??re . Ces mouvements comprennent la cin??tique de l'??nergie dans une substance. Plus pr??cis??ment, la temp??rature thermodynamique de toute quantit?? en vrac de la mati??re est la mesure de l'??nergie cin??tique moyenne d'un certain type de mouvement vibratoire de ses particules constitutives appel??es mouvements de translation. Mouvements de translation sont, mouvements du corps entier ordinaires . espace que les particules se d??placent et l'??nergie d'??change dans des collisions en trois dimensions la figure 1 ci-dessous montre un mouvement de translation dans les gaz; Figure 4 ci-dessous montre un mouvement de translation dans les solides. De temp??rature thermodynamique point z??ro, z??ro absolu, est la temp??rature ?? laquelle les constituants de particules de mati??re sont aussi proches que possible de compl??ter repos; autrement dit, ils ont mouvement minimal, ne conservant que la m??canique quantique mouvement. Z??ro ??nergie cin??tique reste dans une substance au z??ro absolu (voir L'??nergie thermique au z??ro absolu , ci-dessous).
Partout dans le monde scientifique o?? les mesures sont effectu??es en Unit??s SI, temp??rature thermodynamique est mesur??e en kelvins (symbole: K). De nombreux domaines de l'ing??nierie dans le US Cependant, mesurer la temp??rature thermodynamique utilisant la ??chelle Rankine.
Par accord international, le kelvin de l'unit?? et son ampleur sont d??finis par deux points: z??ro absolu et la triple point de Vienne standard Mean Ocean Water (eau avec un m??lange sp??cifi?? de l'hydrog??ne et l'oxyg??ne isotopes). Z??ro absolu, la temp??rature la plus basse possible, est d??finie comme ??tant pr??cis??ment K 0 et -273,15 ?? C . Le point triple de l'eau est d??finie comme ??tant pr??cis??ment 273,16 K et 0,01 ?? C. Cette d??finition fait trois choses:
- Il fixe l'ampleur de l'unit?? de kelvin comme ??tant pr??cis??ment une part ?? 273,16 pi??ces la diff??rence entre le z??ro absolu et le point triple de l'eau;
- Il ??tablit que l'un kelvin a pr??cis??ment la m??me ampleur comme une augmentation de un degr?? sur le Celsius ??chelle; et
- Il ??tablit la diff??rence entre les points nuls des deux balances comme ??tant pr??cis??ment 273,15 kelvins (K = 0 -273,15 ?? C et 273,16 K = 0,01 ?? C).
Temp??ratures exprim??es en kelvins sont convertis en degr??s Rankine simplement en multipliant par 1,8 comme suit: T ?? R = 1,8 T K, o?? T K et T ?? R sont des temp??ratures en degr??s kelvin et de Rankine respectivement. Temp??ratures exprim??es en degr??s Rankine sont convertis en kelvins en divisant par 1,8 comme suit: T K = T ?? R / 1,8.
R??alisation pratique
Bien que les ??chelles de Kelvin et Celsius sont d??finies en utilisant le z??ro absolu (0 K) et le point triple de l'eau (273,16 K et 0,01 ?? C), il est impossible d'utiliser cette d??finition ?? des temp??ratures qui sont tr??s diff??rentes du point triple de l'eau. ITS-90 est alors con??u pour repr??senter le plus fid??lement possible la temp??rature thermodynamique dans toute sa gamme. Beaucoup de diff??rentes conceptions de thermom??tre sont n??cessaires pour couvrir l'ensemble de la gamme. Il se agit notamment h??lium thermom??tres ?? pression de vapeur, les thermom??tres de gaz d'h??lium, thermom??tres ?? r??sistance de platine standard (connu sous le nom Sprts, PRT ou Platium RTD) et thermom??tres de rayonnement monochromatique.
Pour certains types de thermom??tre la relation entre la propri??t?? observ??e (par exemple, la longueur d'une colonne de mercure) et de la temp??rature, est presque lin??aire, donc pour la plupart des fins une ??chelle lin??aire est suffisante, sans ??talonnage point par point. Pour d'autres une courbe d'??talonnage ou l'??quation est n??cessaire. Le thermom??tre ?? mercure, invent?? avant la temp??rature thermodynamique a ??t?? entendu, d??fini ?? l'origine l'??chelle de temp??rature; sa lin??arit?? fait lectures bonne corr??lation avec la temp??rature r??elle, ?? savoir l'??chelle de temp??rature "de mercure" ??tait un ajustement serr?? ?? l'??chelle r??elle.
La relation de la temp??rature, les mouvements, la conduction, et l'??nergie thermique
La nature de l'??nergie cin??tique, un mouvement de translation, et la temp??rature
?? son plus simple, la temp??rature provient de l' ??nergie cin??tique des mouvements vibratoires de mati??re de mandants de particules ( mol??cules , atomes , et particules subatomiques). La vari??t?? compl??te de ces motions cin??tiques, avec ??nergies potentielles de particules, et aussi parfois certains autres types d'??nergie de particules en ??quilibre avec ceux-ci, contribuent total ??nergie interne (vaguement, le thermique ??nerg??tique) dans une substance. Ainsi, l'??nergie peut ??tre stock??e dans un certain nombre de fa??ons dans une substance, mais seulement l'??nergie cin??tique des particules contribue ?? la temp??rature de la substance. Le capacit?? thermique, qui concerne l'apport de chaleur et le changement de temp??rature, est discut??e ci-dessous.
Le rapport de l'??nergie cin??tique, la masse et la vitesse est donn??e par la formule suivante: E k = 1/2 mv 2. En cons??quence, des particules ayant une unit?? de masse mobile ?? une unit?? de vitesse ont exactement la m??me ??nergie cin??tique, et pr??cis??ment la m??me temp??rature, que ceux qui ont quatre fois la masse mais la moiti?? de la vitesse.
Sauf dans le r??gime quantique ?? des temp??ratures extr??mement basses, la temp??rature thermodynamique d'une quantit?? majeure d'une substance (une quantit?? statistiquement significative de particules) est directement proportionnelle ?? l'??nergie cin??tique moyenne moyenne d'un certain type de mouvement de particules connu sous le nom mouvement de translation. Ces mouvements simples dans les trois x, y, z et de les dimensions de l'espace signifie que les particules se d??placent dans les trois spatiale degr??s de libert??. Cette forme particuli??re d'??nergie cin??tique est parfois appel??s temp??rature cin??tique. translation ne est qu'une forme d'??nergie thermique et de gaz est ce qui donne non seulement leur temp??rature, mais aussi leur pression et la grande majorit?? de leur volume. Cette relation entre la temp??rature, la pression et le volume de gaz est ??tabli par le formule pv de loi des gaz parfaits = nRT et est incarn?? dans le lois de gaz.
La mesure dans laquelle l'??nergie cin??tique du mouvement de translation d'un atome ou d'une mol??cule (des particules) individuelle dans un gaz contribue ?? la pression et le volume de gaz qui est une fonction proportionnelle de la temp??rature thermodynamique, tel qu'??tabli par la Constante de Boltzmann (symbole: k B). La constante de Boltzmann concerne ??galement la temp??rature thermodynamique d'un gaz ?? l'??nergie cin??tique moyenne du mouvement de translation d'une particule individuelle de la mani??re suivante:
o??:
 est l'??nergie cin??tique moyenne en joules (J) et se prononce "E bar"
est l'??nergie cin??tique moyenne en joules (J) et se prononce "E bar" - k B = 1,380 6 504 (24) ?? 10 -23 J / K et se prononce "bee sous Kay"
- T est la temp??rature thermodynamique en kelvins (K) et se prononce "Tee"
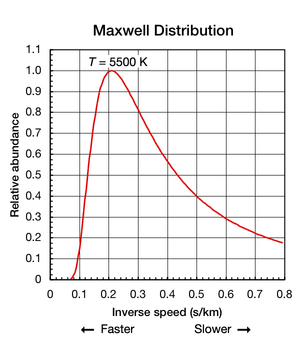
Alors que la constante de Boltzmann est utile pour trouver l'??nergie cin??tique moyenne d'une particule, il est important de noter que m??me si une substance est isol?? et ??quilibre thermodynamique (toutes les pi??ces sont ?? une temp??rature uniforme et pas de chaleur va dans ou hors de celui-ci), les mouvements de translation des atomes et des mol??cules individuelles se produit ?? travers une large gamme de vitesses (voir l'animation dans la figure 1 ci-dessus). A tout instant une, la proportion de particules se d??pla??ant ?? une vitesse donn??e au sein de cette plage est d??termin??e par la probabilit?? telle que d??crite par la Distribution de Maxwell-Boltzmann. Le graphique pr??sent?? ici dans la figure. La figure 2 montre la distribution de vitesse de 5500 K atomes d'h??lium. Ils ont une vitesse la plus probable de 4,780 km / s. Toutefois, une certaine proportion d'atomes ?? un instant donn?? se d??placent plus rapidement tandis que d'autres se d??placent relativement lentement; certains sont momentan??ment ?? l'arr??t virtuel (hors l'axe des x vers la droite). Ce graphique utilise vitesse inverse de son axe des x de sorte que la forme de la courbe peut ??tre ais??ment compar?? ?? des courbes de la Figure 5 ci-dessous. Dans les deux graphiques, z??ro sur l'axe des x repr??sente la temp??rature infinie. En outre, les x et y axe des sur les deux graphiques sont r??duits proportionnellement.
Les hautes vitesses de translation
Bien que les ??quipements de laboratoire tr??s sp??cialis??s est n??cessaire pour d??tecter directement mouvements de translation, les r??sultantes des collisions par des atomes ou des mol??cules de petites particules en suspension dans un fluide produit Mouvement brownien qui peut ??tre vu avec un microscope ordinaire. Les mouvements de translation des particules ??l??mentaires sont tr??s rapides et des temp??ratures proches du z??ro absolu sont tenus d'observer directement. Par exemple, lorsque les scientifiques ?? la NIST atteint une temp??rature froide record de 700 nK (milliardi??mes de kelvin) en 1994, ils ont utilis?? Equipement de r??seau optique laser ?? adiabatique fra??ches c??sium atomes. Ils ont ensuite ??teint les lasers et les vitesses de pi??geage d'atomes directement mesur??es de 7 mm par seconde afin de calculer leur temp??rature. Les formules pour calculer la vitesse et la vitesse de mouvement de translation sont donn??s dans la r??f??rence ci-dessous.
Les mouvements internes de mol??cules et la chaleur sp??cifique

Il ya d'autres formes d'??nergie de chaleur en plus l'??nergie cin??tique du mouvement de translation. Comme on peut le voir dans l'animation ?? droite, les mol??cules sont des objets complexes; ils sont une population d'atomes et de l'agitation thermique peut grever leurs internes liaisons chimiques de trois fa??ons diff??rentes: via rotation, longueur de la liaison, et d'obligations mouvements angulaires. Ce sont tous les types de degr??s de libert?? internes. Cela rend les mol??cules distinctes de substances monoatomiques (constitu??s d'atomes individuels) comme le gaz noble l'h??lium et l'argon , qui ne ont que trois degr??s de libert?? en translation. L'??nergie cin??tique est stock??e dans degr??s internes de mol??cules de la libert??, qui leur donne une temp??rature interne. M??me si ces mouvements sont appel??s interne, les parties externes de mol??cules encore se d??placent plut??t comme le jiggling d'un fixe ballon d'eau. Cela permet l'??change bidirectionnel d'??nergie cin??tique entre les mouvements internes et des mouvements de translation avec chaque collision mol??culaire. En cons??quence, comme la chaleur est ??limin??e ?? partir de mol??cules, tant de leur temp??rature cin??tique (l'??nergie cin??tique du mouvement de translation) et leur temp??rature interne diminue simultan??ment dans des proportions ??gales. Ce ph??nom??ne est d??crit par le equipartition th??or??me, qui stipule que pour toute quantit?? en vrac d'une substance ?? l'??quilibre, l'??nergie cin??tique du mouvement des particules est uniform??ment r??partie entre tous les degr??s de libert?? actifs disponibles pour les particules. Depuis la temp??rature interne de mol??cules sont g??n??ralement ??gale ?? leur temp??rature cin??tique, la distinction est g??n??ralement d'int??r??t que dans l'??tude d??taill??e des non ??quilibre thermodynamique (LTE) ph??nom??nes locaux tels que combustion, la sublimation des solides, et la diffusion de gaz chauds dans un vide partiel.
L'??nergie cin??tique emmagasin??e dans les mol??cules ?? l'int??rieur de substances provoque contiennent plus d'??nergie thermique ?? une temp??rature donn??e et pour absorber l'??nergie thermique suppl??mentaire pour une augmentation de temp??rature donn??e. Ce est parce que toute l'??nergie cin??tique qui est, ?? un instant donn??, li?? ?? des mouvements internes ne est pas ?? ce m??me instant contribuant ?? mouvements de translation des mol??cules. Cette ??nergie cin??tique suppl??mentaire augmente simplement la quantit?? d'??nergie thermique ?? une substance absorbe une ??l??vation de temp??rature donn??e. Cette propri??t?? est connue comme une substance de la capacit?? thermique sp??cifique.
Diff??rentes mol??cules absorbent des quantit??s diff??rentes d'??nergie thermique pour chaque augmentation progressive de la temp??rature; ce qui signifie qu'ils ont des capacit??s thermiques sp??cifiques. Haute capacit?? thermique sp??cifique provient, en partie, parce que les mol??cules de certaines substances poss??dent degr??s de libert?? internes plus que d'autres. Par exemple, la temp??rature ambiante de l'azote , qui est un mol??cule diatomique, dispose de cinq degr??s de libert?? actifs: le mouvement de translation comprenant trois plus deux degr??s de libert?? en rotation interne. Sans surprise, en conformit?? avec le th??or??me d'??quipartition, l'azote a cinq tiers de la capacit?? de chaleur sp??cifique par taupe (un certain nombre de mol??cules) comme les gaz monoatomiques. Un autre exemple est l'essence (voir tableau montrant sa capacit?? de chaleur sp??cifique). L'essence peut absorber une grande quantit?? d'??nergie thermique par mole avec seulement un changement de temp??rature modeste parce que chaque mol??cule comprend une moyenne de 21 atomes et a de nombreux degr??s de libert?? internes cons??quent. M??me grosses mol??cules plus complexes peuvent avoir des dizaines de degr??s de libert?? internes.
La diffusion de la chaleur de l'??nergie: Entropie, phonons et ??lectrons de conduction mobiles

la conduction de la chaleur est la diffusion de l'??nergie thermique ?? partir de parties chaudes d'un syst??me ?? froid. Un syst??me peut ??tre soit une entit?? masse unique ou une pluralit?? d'entit??s discr??tes en vrac. La majeure partie de terme dans ce contexte signifie une quantit?? statistiquement significative de particules (qui peut ??tre une quantit?? microscopique). Chaque fois que l'??nergie thermique se diffuse au sein d'un syst??me isol??, les diff??rences de temp??rature dans le syst??me de diminution (et entropie augmente).
Un m??canisme de conduction de chaleur se produit lorsque notamment un mouvement de translation, la temp??rature sous-jacente de mouvement de particules, transf??re l'??lan de particule ?? particule dans des collisions. Dans les gaz, ces mouvements de translation sont de la nature ci-dessus dans la figure. 1 . Comme on le voit en ce que l'animation, non seulement la dynamique (chaleur) diffuse dans tout le volume du gaz ?? travers les collisions de s??rie, mais des mol??cules ou des atomes entiers peuvent se d??placer vers l'avant dans un nouveau territoire, portant leur ??nergie cin??tique avec eux. Par cons??quent, les diff??rences de temp??rature tout au long ??galiser gaz tr??s rapidement, surtout pour les atomes l??gers ou des mol??cules; convection acc??l??re ce processus encore plus.
Mouvement de translation dans cependant solides, prend la forme de phonons (voir Fig. 4 ?? droite). Phonons sont contraints, paquets d'ondes quantifi??es voyageant ?? la vitesse du son pour une substance donn??e. La mani??re dont les phonons interagissent au sein d'un solide d??termine ses diverses propri??t??s, y compris sa conductivit?? thermique. Dans les solides ??lectriquement isolantes, conduction de la chaleur ?? base de phonon-est g??n??ralement inefficace et ces solides sont consid??r??s comme isolants thermiques (tels que le verre, le plastique, le caoutchouc, la c??ramique, et la roche). Ce est parce que dans les solides, les atomes et les mol??cules sont verrouill??s en place par rapport ?? leurs voisins et ne sont pas libres de se d??placer.
Les m??taux ne sont toutefois pas limit??s ?? la conduction de la chaleur uniquement sur la base phonon. L'??nergie thermique effectue gr??ce m??taux extr??mement rapidement, car au lieu de collisions directes mol??cule ?? mol??cule, la grande majorit?? de l'??nergie thermique est m??di??e par tr??s l??gers, mobiles conduction des ??lectrons . Ce est pourquoi il existe une corr??lation presque parfaite entre les m??taux ' conductivit?? thermique et leur conductivit?? ??lectrique. ??lectrons de conduction impr??gnent m??taux avec leur conductivit?? extraordinaire parce qu'ils sont d??localis??e (ce est ?? dire, ne sont pas li??s ?? un atome sp??cifique) et de se comporter un peu comme une sorte de gaz quantique en raison des effets de ??nergie du point z??ro (pour plus de ZPE, voir la note 1 ci-dessous). En outre, les ??lectrons sont relativement l??gers avec une masse au repos seulement 1/1836 ??me celle d'un proton . Il se agit de la m??me proportion que la 0,22 balle courte (29 grains ou 1,88 g) par rapport ?? l'arme qui tire elle. Comme Isaac Newton a ??crit avec son troisi??me loi du mouvement ,
Loi n ?? 3: Toutes les forces sont associ??s par paires, et ces deux forces sont ??gales en amplitude et en direction oppos??e.
Cependant, une balle acc??l??re plus vite que un fusil donn?? une force ??gale. Depuis ??nergie cin??tique augmente comme le carr?? de la vitesse, la quasi-totalit?? de l'??nergie cin??tique va dans la balle, pas le fusil, m??me si les deux l'exp??rience de la m??me force des gaz propulseurs expansion. De la m??me mani??re, car ils sont beaucoup moins massive, l'??nergie thermique est facilement support?? par les ??lectrons de conduction mobiles. En outre, parce qu'ils sont d??localis??e et tr??s rapide, l'??nergie cin??tique de chaleur conduit tr??s rapidement ?? travers les m??taux avec des ??lectrons de conduction abondantes.
La diffusion de l'??nergie de chaleur: le rayonnement du corps noir
Le rayonnement thermique est un sous-produit des collisions d??coulant de divers mouvements vibratoires d'atomes. Ces collisions entra??nent les ??lectrons des atomes de thermiques ??mettent des photons (connu sous le nom rayonnement du corps noir). Photons sont ??mis quand une charge ??lectrique est acc??l??r??e (comme cela arrive quand les nuages de deux atomes d'??lectrons entrent en collision). M??me mol??cules individuelles avec des temp??ratures internes sup??rieures ?? z??ro absolu ??mettent aussi un rayonnement du corps noir de leurs atomes. Dans ne importe quelle quantit?? en vrac d'une substance ?? l'??quilibre, les photons corps noir sont ??mis ?? travers une gamme de longueurs d'onde dans un spectre qui a une forme de courbe comme Bell appel?? Courbe Planck (voir graphique en. Fig 5 ?? droite). Le sommet d'une courbe de Planck ( la longueur d'onde pic de ??mittance) est situ?? dans une partie particuli??re de la spectre ??lectromagn??tique en fonction de la temp??rature du corps noir. Substances ?? l'extr??me temp??ratures cryog??niques ??mettent aux longueurs d'onde radio longues alors des temp??ratures extr??mement chaudes produisent courte rayons gamma (voir Table des temp??ratures ordinaires ).
Rayonnement du corps noir diffuse l'??nergie de la chaleur dans une substance que les photons sont absorb??s par des atomes voisins, le transfert de la dynamique du processus. Photons corps noir aussi ??chapper facilement d'une substance et peuvent ??tre absorb??s par le milieu ambiant; l'??nergie cin??tique est perdue dans le processus.
Comme ??tabli par le Loi de Stefan-Boltzmann, l'intensit?? des augmentations de rayonnement du corps noir comme la quatri??me puissance de la temp??rature absolue. Ainsi, un corps noir ?? 824 K (un peu moins de rouge sombre incandescent) ??met 60 fois le radiants puissance comme il le fait ?? 296 K (temp??rature ambiante). Ce est pourquoi on peut si facilement sentir la chaleur rayonnante des objets chauds ?? distance. Aux temp??ratures plus ??lev??es, telles que celles trouv??es dans une lampe ?? incandescence, rayonnement du corps noir peut ??tre le principal m??canisme par lequel l'??nergie de la chaleur se ??chappe un syst??me.
Table des temp??ratures thermodynamiques
La gamme compl??te de l'??chelle de temp??rature thermodynamique, du z??ro absolu ?? absolu chaud, et quelques points notables entre eux sont pr??sent??s dans le tableau ci-dessous.
| kelvin | ??mittance pic longueur d'onde de photons corps noir | |
| Z??ro absolu (Pr??cis??ment par d??finition) | 0 K | ∞ |
| Coldest mesur??e temp??rature | 450 pK | 6400 km |
| Un millikelvin (Pr??cis??ment par d??finition) | 0,001 K | 2,897 77 m??tres (Radio, Bande FM) |
| Eau de point triple (Pr??cis??ment par d??finition) | 273,16 K | 10,608.3 nm (Longueur d'onde longue IR) |
| Lampe ?? incandescence B | 2500 K | 1160 nm (Near infrarouge) C |
| Sun surface visible C | 5778 K | 501,5 nm ( Feu vert ) |
| Eclair de canal | 28000 K | 100 nm (Far Ultraviolet la lumi??re) |
| Le noyau de Sun | 16 MK | 0,18 nm ( Les rayons X) |
| Bombe H (Temp??rature maximale) | 350 MK | 8,3 ?? 10 -3 nm ( Les rayons gamma) |
| Sandia National Labs ?? Z machine D | 2 GK | 1,4 ?? 10 -3 nm (rayons gamma) |
| Base d'un de masse ??lev??e STAR sur son dernier jour | 3 GK | 1 x 10 -3 nm (rayons gamma) |
| Fusion binaire neutron syst??me d'??toiles | 350 GK | 8 ?? 10 -6 nm (rayons gamma) |
| Sursaut gamma prog??niteurs | 1 TK | 3 ?? 10 -6 nm (rayons gamma) |
| Lourds relativistes Ion Collider | 1 TK | 3 ?? 10 -6 nm (rayons gamma) |
| Protons du CERN contre la collisions noyau | 10 savoirs traditionnels | 3 ?? 10 -7 nm (rayons gamma) |
| Univers 5,391 ?? 10 -44 s apr??s la Big Bang | 1,417 ?? 10 32 K | 1,616 ?? 10 -26 nm (Fr??quence Planck) |
A La valeur K 2500 est approximative.
B Pour un vrai noir (qui ne sont pas filaments de tungst??ne). l'??missivit?? de filaments de tungst??ne est sup??rieure aux longueurs d'onde plus courtes, ce qui les rend plus blancs.
C la temp??rature de la photosph??re efficace.
D Pour un vrai noir (qui ne ??tait pas le plasma). ??mission dominante de la machine ?? Z provient de 40 ??lectrons MK (??missions rayons X mous) dans le plasma.
La chaleur de changement de phase

L'??nergie cin??tique du mouvement des particules ne est qu'un contributeur ?? l'??nergie totale de chaleur dans une substance; un autre est les transitions de phase, qui sont le l'??nergie potentielle de liaisons mol??culaires qui peuvent se former dans une substance en refroidissant (par exemple pendant et condensation cong??lation). L'??nergie thermique requise pour une transition de phase est appel??e . chaleur latente Ce ph??nom??ne peut plus facilement ??tre saisie en le consid??rant dans le sens inverse: la chaleur latente est l'??nergie n??cessaire pour rompre les liaisons chimiques (tels que cours ??vaporation et fusion). Presque tout le monde est familier avec les effets de transitions de phase; par exemple, la vapeur ?? 100 ?? C peut causer de graves br??lures beaucoup plus rapidement que l'air 100 ?? C ?? partir d'un s??che-cheveux. Cela se produit car une grande quantit?? de chaleur latente est lib??r??e sous forme de vapeur se condense en eau liquide sur la peau.
Bien que l'??nergie thermique est lib??r??e ou absorb??e au cours de transitions de phase, purs ??l??ments chimiques , compos??s , et eutectique alliages pr??sentent pas de changement de la temp??rature que ce soit alors ils les subissent (voir Fig. 7, ci-dessous ?? droite). Consid??rez un type particulier de transition de phase: fusion. Quand un solide est en train de fondre, r??seau cristallin liaisons chimiques sont d??compos??s; la substance est en train de passer de ce qui est connu comme un ??tat plus ordonn?? ?? un ??tat moins ordonn??. Dans la Fig. 7, la fonte des glaces est repr??sent?? au sein de la bo??te en bas ?? gauche la position du bleu au vert.
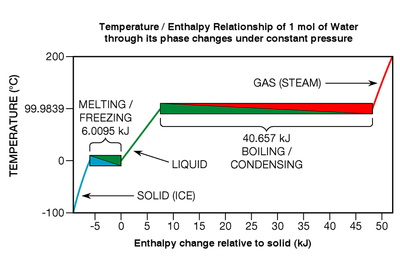
?? un moment donn?? thermodynamique sp??cifique, le point de fusion (qui est de 0 ?? C ?? travers une large gamme de pression dans le cas de l'eau), tous les atomes ou mol??cules sont, en moyenne, au seuil maximum d'??nergie de leurs liaisons chimiques peut supporter sans rompre du treillis. Les liaisons chimiques sont des forces toutes-ou-rien: soit ils d??tiennent rapide, ou se casser; il ne existe aucun ??tat entre-deux. Par cons??quent, lorsqu'une substance est ?? son point de fusion, tous les joule d'??nergie de la chaleur ajout??e ne rompt les liens d'une quantit?? sp??cifique de ses atomes ou de mol??cules, les convertir dans un liquide de pr??cis??ment la m??me temp??rature; pas d'??nergie cin??tique est ajout?? ?? un mouvement de translation (qui est ce qui donne substances leur temp??rature). L'effet est un peu comme popcorn: ?? une certaine temp??rature, l'??nergie thermique suppl??mentaire ne peut pas faire les noyaux plus chaud jusqu'?? ce que la transition (popping) est termin??e. Si le processus est invers?? (comme dans le gel d'un liquide), l'??nergie calorifique doit ??tre retir?? de la substance.
Comme indiqu?? plus haut, l'??nergie thermique n??cessaire pour une transition de phase est appel??e chaleur latente. Dans les cas sp??cifiques de fusion et de cong??lation, il est appel?? enthalpie de fusion ou de la chaleur de fusion. Si les liaisons mol??culaires dans un r??seau cristallin sont fortes, la chaleur de fusion peut ??tre relativement grande, typiquement dans la gamme de 6 ?? 30 kJ par mole de l'eau et la plupart des ??l??ments m??talliques. Si la substance est l'un des gaz monoatomiques, (qui ont peu tendance ?? former des liaisons mol??culaires) la chaleur de fusion est plus faible, allant de 0,021 ?? 2,3 kJ par mole. Relativement parlant, les transitions de phase peuvent ??tre des ??v??nements vraiment ??nergiques. Pour faire fondre compl??tement glace ?? 0 ?? C dans l'eau ?? 0 ?? C, il faut ajouter environ 80 fois l'??nergie de chaleur est n??cessaire pour augmenter la temp??rature de la m??me masse d'eau liquide par un degr?? Celsius. Les ratios des m??taux sont encore plus grandes, typiquement dans la gamme de 400 ?? 1200 fois. Et la transition de phase de ??bullition est beaucoup plus ??nergique que la cong??lation. Par exemple, l'??nergie n??cessaire pour faire bouillir compl??tement ou vaporiser de l'eau (ce qui est connu en tant que enthalpie de vaporisation) est environ 540 fois celle requise pour une hausse d'un degr??.
Enthalpie importante de l'eau de vaporisation est pourquoi sa peau peut ??tre br??l?? si rapidement que de la vapeur se condense sur elle (rubrique du rouge au vert sur la Fig. 7 ci-dessus). Dans la direction oppos??e, ce est pourquoi sa peau est fra??che que l'eau liquide sur elle se ??vapore (un processus qui se produit ?? un sous-ambiante temp??rature de bulbe humide qui d??pend de humidit?? relative). Enthalpie tr??s ??nergique de l'eau de vaporisation est ??galement un facteur important qui sous-tend la raison pour laquelle les couvertures de piscine solaires (flottants, des couvertures isol??s qui couvrent piscines lorsqu'il ne est pas en cours d'utilisation) sont si efficaces ?? r??duire les co??ts de chauffage: ils emp??chent l'??vaporation. Par exemple, l'??vaporation de seulement 20 mm d'eau d'un bassin 1,29 m??tres de profondeur refroidit son eau 8,4 degr??s Celsius (15,1 ?? F).
L'??nergie interne
L'??nergie cin??tique totale de tous les mouvements des particules, y compris celle des ??lectrons de conduction, en plus de l'??nergie potentielle de changements de phase, ainsi que ??nergie du point z??ro comprennent la l'??nergie d'une substance, qui est son ??nergie thermique totale. L'??nergie interne terme ne doit pas ??tre confondue avec degr??s de libert?? internes. Alors que les degr??s de libert?? internes de mol??cules se r??f??re ?? un endroit particulier o?? l'??nergie cin??tique est li??e, l'??nergie interne d'une substance comprend toutes les formes d'??nergie thermique.

L'??nergie thermique au z??ro absolu
Comme une substance se refroidit, les diff??rentes formes d'??nergie thermique et leurs effets connexes diminuer simultan??ment en amplitude: la chaleur latente de disponibles transitions de phase sont lib??r??s comme une substance passe d'un ??tat moins ordonn?? ?? un ??tat plus ordonn??; les mouvements de translation des atomes et des mol??cules diminuent (leur temp??rature cin??tique diminue); les mouvements internes de mol??cules diminuent (leur temp??rature interne diminue); ??lectrons de conduction (si la substance est un conducteur ??lectrique) voyager un peu plus lent; et le pic de rayonnement noir de corps ??mittance longueur d'onde augmente (l'??nergie des photons diminue). Lorsque les particules d'une substance sont aussi proches que possible de compl??ter repos et de ne retenir que le mouvement m??canique quantique ZPE-induite, la substance est ?? la temp??rature du z??ro absolu (T = 0).
Notez que, tandis que le z??ro absolu est le point z??ro temp??rature thermodynamique et est ??galement le moment o?? les constituants des particules de la mati??re ont mouvement minimal, z??ro absolu ne est pas n??cessairement le point ?? laquelle une substance contient z??ro ??nergie thermique; il faut ??tre tr??s pr??cis avec ce que l'on entend par ??nergie thermique. Souvent, tous les changements de phase qui peuvent survenir dans une substance, auront eu lieu au moment o?? il atteint z??ro absolu. Cependant, ce ne est pas toujours le cas. Notamment, T = 0 h??lium reste liquide ?? la pression ambiante et doit ??tre sous une pression d'au moins 25 bar (2,5 MPa) ?? cristalliser. Ce est parce que la chaleur de l'h??lium de la fusion (l'??nergie requise pour faire fondre la glace de l'h??lium) est si faible (seulement 21 joules par mole) que l'effet de mouvement induisant des ??nergie du point z??ro est suffisante pour l'emp??cher de geler ?? des pressions inf??rieures. Seulement si dans au moins 25 bars (2,5 MPa) de la pression sera cette ??nergie de chaleur latente lib??r??e comme le gel d'h??lium en se approchant de z??ro absolu. Une autre complication est que beaucoup de solides changent leur structure cristalline ?? des arrangements plus compacts ?? des pressions tr??s ??lev??es (jusqu'?? des millions de bars, ou des centaines de gigapascals). Ils sont connus comme les transitions de phase solide-solide dans lequel la chaleur latente est lib??r??e comme un r??seau cristallin des modifications ?? un, compact une thermodynamiquement plus favorable.
Les complexit??s ci-dessus font des d??clarations g??n??rales plut??t lourdes concernant l'??nergie interne en T = 0 substances. Ind??pendamment de la pression mais, ce qui peut ??tre dit, ce est que au z??ro absolu, tous les solides avec un r??seau cristallin plus bas d'??nergie tels ceux avec un plus compacte arrangement (voir Fig. 8, ci-dessus ?? gauche) contient ??nergie minimale, pour ne retenir que celle due au contexte toujours pr??sent d'??nergie du point z??ro. On peut aussi dire que pour une substance donn??e ?? pression constante, le z??ro absolu est le point le plus bas enthalpie (une mesure du potentiel de travail qui prend de l'??nergie interne, la pression et le volume en consid??ration). Enfin, il est toujours vrai de dire que tous les T = 0 substances contiennent z??ro ??nergie cin??tique de la chaleur.
Les applications pratiques de temp??rature thermodynamique

Temp??rature thermodynamique est utile non seulement pour les scientifiques, il peut aussi ??tre utile pour les la??cs dans de nombreuses disciplines impliquant des gaz. En exprimant les variables en termes absolus et en appliquant Loi de Gay-Lussac de proportionnalit?? temp??rature / pression, des solutions aux probl??mes quotidiens sont simples; par exemple, le calcul de la fa??on dont un changement de temp??rature influe sur la pression ?? l'int??rieur d'un pneu d'automobile. Si le pneu a une pression relativement froid de 200 kPa-Gage, puis en termes absolus (par rapport ?? un vide), sa pression est de 300 kPa absolu. La temp??rature ambiante ("froid" en termes de pneus) est 296 K. Si la pression des pneus est de 20 ?? C plus chaud (20 kelvins), la solution est calcul??e comme 316 K / 296 K = 6,8% plus grande temp??rature thermodynamique et la pression absolue; ce est une pression de 320 kPa-absolue, qui est de 220 kPa-Gage.
D??finition de temp??rature thermodynamique
Strictement parlant, la temp??rature d'un syst??me est bien d??finis que si ses particules ( atomes , mol??cules , ??lectrons , photons ) sont ?? l'??quilibre, de sorte que leur ??nergie ob??issent ?? une Distribution de Boltzmann (ou sa m??canique quantique contrepartie). Il existe de nombreuses ??chelles possibles de temp??rature, provenant d'une vari??t?? d'observations de ph??nom??nes physiques. La temp??rature thermodynamique peut ??tre montr?? pour avoir des propri??t??s sp??ciales, et en particulier peut ??tre vu pour ??tre d??finie de mani??re unique (jusqu'?? un facteur multiplicatif constant) en consid??rant la efficacit?? de id??alis??e moteurs thermiques. Ainsi, la T 2 / T 1 des deux temp??ratures T 1 et T 2 est le m??me rapport ?? toutes les ??chelles absolues.
Librement a d??clar??, la temp??rature contr??le le flux de chaleur entre deux syst??mes, et l' univers dans son ensemble, comme avec ne importe quel syst??me naturel, a tendance ?? progresser de mani??re ?? maximiser l'entropie . Cela donne ?? penser qu'il devrait y avoir une relation entre la temp??rature et l'entropie. Pour ??lucider cela, consid??rons d'abord la relation entre la chaleur, le travail et la temp??rature. Une fa??on d'??tudier ce est d'analyser un moteur thermique, qui est un dispositif destin?? ?? convertir la chaleur en travail m??canique, tel que le Cycle de Carnot. Ces fonctions d'un des moteurs de la chaleur en utilisant un gradient de température entre une haute température T H et une basse température T C de générer du travail, et le travail effectué (par cycle, par exemple) par le moteur thermique est égale à la différence entre l'énergie thermique q H mettre en le système à la température élevée et la chaleur q C éjecté à la basse température (dans ce cycle). Le rendement du moteur est divisée par le travail de la chaleur du système mis en ou
où w cy est le travail effectué par cycle. Ainsi, l'efficacité ne dépend que de q C / q H .
Le th??or??me de Carnot stipule que tous les moteurs r??versibles fonctionnant entre les m??mes r??servoirs de chaleur sont ??galement efficaces.Ainsi, un moteur de chaleur réversible fonctionnant entre les températuresT 1etT 2doit avoir la même efficacité, ce qui est à dire, l'efficacité est la fonction des seules températures
En outre, un moteur thermique réversible fonctionnant entre les températures T 1 et T 3 doit avoir la même efficacité que l'un constitué par les deux cycles, une entre T 1 et un autre (intermédiaire) la température T 2 , et la seconde entre T 2 et T 3 . Un moyen rapide de voir ce que ce devrait pas être le cas, alors l'énergie (sous forme de Q ) seront gaspillés ou acquise, résultant en différents rendements globaux à chaque fois un cycle est divisé en cycles de composants; clairement un cycle peut être composé d'un nombre quelconque de cycles plus petits.
Avec cette compréhension deQ 1,Q 2etQ 3, nous notons aussi que mathématiquement,
Mais la première fonction est PAS une fonction de T 2 , donc le produit des deux dernières fonctions DOIT entraîner le retrait de T 2 comme une variable. Le seul moyen est donc de définir la fonction f comme suit:
et
de sorte que
dire le rapport entre la puissance thermique ??chang??e est une fonction des temp??ratures respectives au cours de laquelle ils se produisent.Nous pouvons choisir toute fonction monotone pour notre ;il est une question de commodité et de la convention que nous choisissons
;il est une question de commodité et de la convention que nous choisissons .Choisir ensuiteunetempérature de référence fixe (c.-à-point triple de l'eau), nous établissons l'échelle de température thermodynamique.
.Choisir ensuiteunetempérature de référence fixe (c.-à-point triple de l'eau), nous établissons l'échelle de température thermodynamique.
Il est à noter que cette définition coïncide avec celui de la dérivation des gaz parfaits; il est aussi cette définition de la température thermodynamique qui nous permet de représenter le rendement de Carnot en termes de T H et T C , et donc tirer que le (complet) cycle de Carnot est isentropique:
En substituant cette arrière dans notre première formule d'efficacité donne une relation en termes de température:
Notez que pour T C = 0, le rendement est de 100% et que l'efficacité devient supérieure à 100% pour T C <0, ce qui ne sont pas réalistes cas. En soustrayant le côté droit de l'équation 4 de la partie médiane et donne réorganisation
o?? le signe n??gatif indique thermique ??ject?? du syst??me.La généralisation de cette équation estClausius théorème, ce qui suggère l'existence d'unefonction état??????S(ie, une fonction qui ne dépend que de l'état du système, et non pas sur la façon dont il a atteint cet état) défini (à une constante additive) par
où l'indice indique le transfert de chaleur dans un processus réversible. La fonction S correspond à l' entropie du système, mentionné précédemment, et le changement de S autour d'un cycle est égal à zéro (ce ??????qui est nécessaire pour toute fonction d'état). L'équation 5 peut être réarrangé pour obtenir une définition alternative pour la température en termes d'entropie et de la chaleur (pour éviter la boucle logique, nous devrions d'abord définir l'entropie par la mécanique statistique):
Pour un système dans lequel l'entropieSest une fonctionS(E) de son énergieE, la température thermodynamiqueTest donc donnée par
de sorte que l'inverse de la température thermodynamique est le taux d'augmentation de l'entropie de l'énergie.
Histoire
- Ca. 485 BC: Parménide dans son traité «De la Nature" postulé l'existente de frigidum primum , une source de substance élémentaire hypothétique de tout refroidissement ou de froid dans le monde.
- 1702-1703: Guillaume Amontons (1663-1705) a publié deux documents qui peuvent être utilisés pour le crédit comme étant le premier chercheur à déduire l'existence d'un (thermodynamique) échelle de température fondamentale avec un zéro absolu. Il a fait la découverte tout en cherchant à améliorer les thermomètres d'air en usage à l'époque. Ses thermomètres J-tubes constitués d'une colonne de mercure qui a été soutenu par une masse fixe de l'air piégé dans la partie de détection du thermomètre. En termes thermodynamiques, ses thermomètres invoqués la relation entre le volume / température du gaz sous pression constante. Ses mesures du point d'eau et le point de glace de fusion ébullition ont montré que, indépendamment de la masse d'air emprisonné à l'intérieur de ses thermomètres ou le poids de mercure de l'air a été soutenu, la réduction du volume de l'air au point de la glace était toujours le même rapport . Cette observation a conduit à postuler qu'une réduction suffisante de la température permettrait de réduire le volume d'air à zéro. En fait, ses calculs prévoyaient que le zéro absolu était équivalente à -240 ° C-seulement 33.15 degrés courts de la vraie valeur de -273,15 ° C.
- 1742: Anders Celsius (1701-1744) a créé une version «à rebours» de l'échelle moderne de température en degrés Celsius. Dans échelle originale de Celsius, zéro représenté le point d'ébullition d'eau et 100 représentaient le point de fonte des glaces. Dans son document Observations de deux degrés persistants sur un thermomètre, il a raconté ses expériences montrant que le point de fusion de la glace était effectivement affectée par la pression. Il a également déterminé avec une précision remarquable comment le point d'ébullition de l'eau varie en fonction de la pression atmosphérique. Il a proposé que le zéro sur son échelle de température (le point d'ébullition de l'eau) serait calibré à la pression barométrique moyenne au niveau moyen de la mer.
- 1744: Coïncidant avec la mort de Anders Celsius, le célèbre botaniste Carl von Linné (1707-1778) effectivement inversé l'échelle de Celsius lors de la réception de son premier thermomètre avec une échelle où zéro représenté le point de glace et 100 point d'ébullition de l'eau représenté fusion. Le sur-mesure linnaeus-thermomètre , pour une utilisation dans ses serres, a été faite par Daniel Ekström, premier fabricant suédois d'instruments scientifiques à l'époque. Pour les 204 prochaines années, les communautés scientifiques et dans le monde entier thermométrie référence à cette échelle que l' échelle centigrade . Les températures sur l'échelle centigrade ont été souvent rapportés simplement comme degrés ou, si une plus grande spécificité a été souhaité, degrés centigrades . Le symbole des valeurs de température de cette ampleur était ° C (en plusieurs formats au fil des ans). Parce que le terme centigrades était aussi le nom de langue française pour une unité de mesure d'angle (un centième d'un angle droit) et avait une connotation semblable dans d'autres langues, le terme «degré centésimal" a été utilisé lors de très précis, un langage sans ambiguïté était requis par les organismes de normalisation internationaux tels que le Bureau international des Poids et Mesures (BIPM). Le 9e CGPM ( Conférence générale des poids et mesures ( Conférence générale des Poids et Mesures ) et le (CIPM Comité international des poids et mesures ( Comité international des Poids et Mesures ) a officiellement adopté degré Celsius (symbole: ° C) en 1948.
- 1777: Dans son livre Pyrometrie (Berlin: Haude & Spener 1779) a complété quatre mois avant sa mort, Johann Heinrich Lambert (1728-1777), parfois appelé à tort comme Joseph Lambert, a proposé une échelle de température absolue basée sur la pression / température relation d'un volume fixe de gaz. Cela est différent de la relation entre le volume / température de gaz sous pression constante que Guillaume Amontons découvert 75 années plus tôt. Lambert a déclaré que le zéro absolu était le point où une simple extrapolation linéaire atteint la pression du gaz zéro et était égale à -270 ° C.
- Circa 1787: Malgré le travail de Guillaume Amontons 85 années plus tôt, Jacques Alexandre César Charles (1746-1823) est souvent crédité de découvrir, mais non l'édition, que le volume d'un gaz sous pression constante est proportionnelle à sa température absolue. La formule qu'il a créé était V 1 / T 1 = V 2 / T 2 .
- 1802: Louis Joseph Gay-Lussac (1778-1850) ouvrage publié (en reconnaissant les notes de laboratoire inédites de Jacques Charles quinze ans plus tôt) décrivant comment le volume de gaz sous les variations de pression constants linéairement avec son absolue (thermodynamique) la température. Ce comportement est appelé la loi de Charles et est l'un des lois de gaz. Sa sont les formules du premier connus pour utiliser le numéro 273 pour le coefficient de dilatation du gaz par rapport au point de glace de fusion (ce qui indique que le zéro absolu était équivalente à -273 ° C).
- 1848: William Thomson , (1824-1907), également connu comme Lord Kelvin, a écrit dans son journal, sur une échelle thermométrique absolue, de la nécessité d'une échelle par laquelle infinie froid (zéro absolu) était point zéro de l'échelle, et qui a utilisé le degré Celsius pour son incrément de l'unité. Comme Gay-Lussac, Thomson a calculé que le zéro absolu était équivalente à -273 ° C sur les thermomètres de l'air de l'époque. Cette échelle absolue est connu aujourd'hui comme l'échelle de température thermodynamique Kelvin. Il est à noter que la valeur de Thomson de -273 a été en fait dérivé de 0,00366, qui était le coefficient de dilatation acceptée de gaz par degré Celsius par rapport au point de glace. L'inverse de -0,00366 exprimé à cinq chiffres significatifs est -273,22 ° C, ce qui est remarquablement proche de la vraie valeur de -273,15 ° C.
- 1859: William John Macquorn Rankine (1820-1872) a proposé une échelle thermodynamique de température similaire à William Thomson, mais qui a utilisé le degré Fahrenheit pour son incrément de l'unité. Cette échelle absolue est connu aujourd'hui comme l' échelle de température thermodynamique Rankine.
- 1877-1884: Ludwig Boltzmann (1844-1906) a fait d'importantes contributions à la thermodynamique grâce à une compréhension du rôle que la cinétique de particules et de rayonnement du corps noir joué. Son nom est maintenant attaché à plusieurs des formules utilisées aujourd'hui dans la thermodynamique.
- Circa 1930:expériences de thermométrie de gaz soigneusement calibrés au point de glace et de point d'ébullition de l'eau de fusion a montré que le zéro absolu était équivalent à -273,15 ° C.
- 1948: Résolution 3 de la 9e CGPM (Conférence Générale des Poids et Mesures, également connu sous le nom Conférence générale des poids et mesures) fixe le point triple de l'eau précisément à 0,01 ° C. A cette époque, le point triple avait toujours pas de définition formelle pour sa valeur kelvin équivalent, dont la résolution a déclaré "sera fixée à une date ultérieure". L'implication est que si la valeur du zéro absolu mesuré dans les années 1930 était vraiment -273,15 ° C, alors le point triple de l'eau (0,01 ° C) a été équivalent à 273,16 K. En outre, à la fois le CIPM (Comité international des Poids et Mesures , également connu comme le Comité international des poids et mesures) et la CGPM a officiellement adopté le nom Celsius pour le degré Celsius et l' échelle de température Celsius .
- 1954: Résolution 3 de la 10e Conférence générale a donné l'échelle Kelvin sa définition moderne en choisissant le point triple de l'eau comme son deuxième point de définition et lui a donné une température de précision 273,16 kelvin (ce qui a été écrit à 273,16 degrés Kelvin à l'époque). Ceci, en combinaison avec la Résolution 3 de la 9e CGPM, a eu pour effet de définir le zéro absolu comme étant précisément zéro kelvin et de -273,15 ° C.
- 1967/1968: Résolution 3 de la 13e CGPM rebaptisé l'incrément de l'unité de température thermodynamique kelvin , symbole K, en remplacement de degré absolu , symbole ° K. En outre, se sentir utile de définir plus explicitement l'ampleur de l'augmentation de l'unité, la 13e CGPM a également décidé dans la résolution 4 que «Le kelvin, unité de température thermodynamique, est la fraction 1 / 273,16 de la température thermodynamique du point triple de l'eau ».
- 2005:Le CIPM (Comité International des Poids et Mesures, aussi connu comme leComité international des poids et mesures)a affirmé que, pour les fins de la délimitation de la température du point triple de l'eau, la définition de l'échelle de température thermodynamique Kelvin se réfère à l'eau ayant une composition isotopique définie comme étant précisément égale à la spécification nominale deVienne standard Mean Ocean Water.