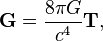Introduction ?? la relativit?? g??n??rale
Renseignements g??n??raux
SOS Enfants, qui se d??roule pr??s de 200 sos ??coles dans le monde en d??veloppement, a organis?? cette s??lection. Avant de vous d??cider ?? propos de parrainer un enfant, pourquoi ne pas en apprendre davantage sur diff??rents organismes de parrainage premier ?
| La relativit?? g??n??rale |
|---|
 |
| Introduction Formulation math??matique Ressources |
Concepts fondamentaux |
Ph??nom??nes Probl??me de Kepler ?? Objectifs ?? Flots Cadre tra??ner ?? Effet g??od??sique Event horizon ?? Singularit?? Trou noir |
??quations Approximation des champs faibles Formalisme post-newtonien ??quation d'Einstein ??quation g??od??sique ??quations de Friedmann Formalisme ADM BSSN formalisme ??quation de Hamilton-Jacobi-Einstein |
Th??ories avanc??es Kaluza-Klein La gravit?? quantique |
Solutions Schwarzschild Reissner-Nordstr??m ?? G??del Kerr ?? Kerr-Newman Kasner ?? Taub-NUT ?? Milne ?? Robertson-Walker pp-ondes ?? la poussi??re van Stockum |
Les scientifiques Einstein ?? Lorentz ?? Hilbert ?? Poincar?? ?? Schwarzschild ?? ?? Sitter Reissner ?? Nordstr??m ?? Weyl ?? Eddington ?? Friedman ?? Milne ?? Zwicky ?? Lema??tre ?? G??del ?? Wheeler ?? Robertson ?? Bardeen ?? Walker ?? Kerr ?? Chandrasekhar ?? Ehlers ?? Penrose ?? Hawking ?? Taylor ?? Hulse ?? Stockum ?? Taub ?? Nouvel Homme Yau ?? Thorne autres |
Spacetime Spacetime Minkowski espace-temps diagrammes de Spacetime Spacetime en relativit?? g??n??rale |
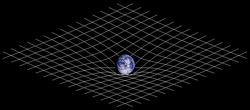
La relativit?? g??n??rale est une th??orie de la gravitation qui a ??t?? d??velopp?? par Albert Einstein entre 1907 et 1915. Selon la relativit?? g??n??rale, l'attraction gravitationnelle des masses observ??e entre les r??sultats de leur d??formation de espace et le temps.
Au d??but du 20??me si??cle, Loi universelle de la gravitation avait ??t?? accept??e pour plus de deux cents ans comme une description valide de la force gravitationnelle entre les masses. Dans le mod??le de Newton, la gravit?? est le r??sultat d'une force d'attraction entre des objets massifs. Bien que m??me Newton a ??t?? troubl?? par la nature inconnue de cette force, le cadre de base a ??t?? extr??mement fructueuse ?? d??crire le mouvement.
Exp??riences et observations montrent que la description de la gravitation d'Einstein repr??sente plusieurs effets qui sont inexpliqu??es par la loi de Newton, comme les anomalies de minutes dans le orbites de Mercure et d'autres plan??tes . La relativit?? g??n??rale pr??dit ??galement de nouveaux effets de la gravit??, tels que ondes gravitationnelles, lentille gravitationnelle et un effet de la gravit?? sur le temps connu sous le nom gravitationnelle dilatation du temps. Beaucoup de ces pr??dictions ont ??t?? confirm??es par l'exp??rience, tandis que d'autres font l'objet de recherches en cours. Par exemple, bien qu'il y ait des preuves indirectes d'ondes gravitationnelles, la preuve directe de leur existence est toujours recherch?? par plusieurs ??quipes de scientifiques dans des exp??riences comme le LIGO et GEO 600 projets.
La relativit?? g??n??rale est devenue un outil essentiel dans moderne astrophysique . Il constitue la base de la compr??hension actuelle de trous noirs , les r??gions de l'espace o?? l'attraction gravitationnelle est si forte que m??me la lumi??re ne peut se ??chapper. Leur forte gravit?? est pens?? pour ??tre responsable de l'intense rayonnement ??mis par certains types d'objets astronomiques (tels que noyaux actifs de galaxies ou microquasars). La relativit?? g??n??rale est ??galement inscrit dans le cadre de la norme Big Bang mod??le de la cosmologie .
Bien que la relativit?? g??n??rale ne est pas la seule th??orie relativiste de la gravit??, il est le plus simple telle th??orie qui est compatible avec les donn??es exp??rimentales. N??anmoins, un certain nombre de questions ouvertes restent, dont la plus fondamentale est de savoir comment la relativit?? g??n??rale peut ??tre concili??e avec les lois de la physique quantique pour produire une th??orie compl??te et coh??rente de l'auto- la gravit?? quantique.
De particuli??re ?? la relativit?? g??n??rale
En Septembre 1905, Albert Einstein publie sa th??orie de la relativit?? restreinte , qui concilie les lois du mouvement de Newton avec ??lectrodynamique (L'interaction entre les objets avec charge ??lectrique ). La relativit?? sp??ciale a introduit un nouveau cadre pour l'ensemble de la physique en proposant de nouveaux concepts de espace et le temps. Certaines th??ories physiques puis accept??es ??taient incompatibles avec ce cadre; un exemple cl?? ??tait la th??orie de Newton sur la gravit?? , qui d??crit l'attraction mutuelle v??cue par les organismes en raison de leur masse.
Plusieurs physiciens, dont Einstein, cherch?? une th??orie qui r??concilierait la loi de la gravitation de Newton et de la relativit?? restreinte. Seulement la th??orie d'Einstein se est av??r?? ??tre conforme aux exp??riences et observations. Pour comprendre les id??es de base de la th??orie, il est instructif de suivre la pens??e d'Einstein entre 1907 et 1915, de son simple, pens?? exp??rience impliquant un observateur en chute libre ?? sa th??orie enti??rement g??om??trique de gravit??.
Principe d'??quivalence
Une personne dans un en chute libre ascenseur ??prouve apesanteur, et des objets soit flotter immobile ou la d??rive ?? une vitesse constante. Puisque tout dans l'ascenseur est en baisse ensemble, aucun effet gravitationnel peut ??tre observ??e. De cette fa??on, les exp??riences d'un observateur en chute libre sont indiscernables de ceux d'un observateur dans l'espace profond, loin de toute source importante de gravit??. Ces observateurs sont les observateurs privil??gi??s (??inertie??) d??crit Einstein dans sa th??orie de la relativit?? restreinte : les observateurs pour lesquels la lumi??re se d??place le long des lignes droites ?? vitesse constante.
Einstein l'hypoth??se que les exp??riences similaires de apesanteur observateurs et des observateurs d'inertie dans la relativit?? restreinte repr??sentaient une propri??t?? fondamentale de la gravit??, et il a fait ce la pierre angulaire de sa th??orie de la relativit?? g??n??rale, formalis?? dans son principe d'??quivalence. Grosso modo, les principe stipule que une personne dans un ascenseur en chute libre ne peut pas dire qu'il est en chute libre. Chaque exp??rience dans un environnement en chute libre a les m??mes r??sultats que ce serait pour un observateur au repos ou en mouvement uniforme dans l'espace profond, loin de toutes les sources de gravit??.
Gravit?? et acc??l??ration

La plupart des effets de la gravit?? disparaissent en chute libre, mais les effets qui semblent les m??mes que celles de gravit?? peuvent ??tre produites par une acc??l??ration de cadre de r??f??rence. Un observateur dans une pi??ce ferm??e ne peut pas dire lequel des ??nonc??s suivants est vrai:
- Objets tombent sur le sol parce que la salle est pos??e sur la surface de la Terre et les objets sont tir??s vers le bas par gravit??.
- Objets tombent sur le sol parce que la salle est ?? bord d'une fus??e dans l'espace, qui se acc??l??re ?? 9,81 m / s 2 et est loin d'??tre une source potentielle de gravit??. Les objets sont tir??s vers le sol par la m??me ??force d'inertie?? qui appuie le conducteur d'une voiture acc??l??rant dans le dossier de son si??ge.
Inversement, tout effet observ?? dans un cadre de r??f??rence acc??l??r??e doit ??galement ??tre observ?? dans un champ gravitationnel de la r??sistance correspondant. Ce principe a permis Einstein pour pr??dire plusieurs nouveaux effets de gravit?? en 1907, comme expliqu?? dans la section suivante .
Un observateur dans un cadre de r??f??rence acc??l??r??e doit pr??senter ce que les physiciens appellent forces fictives pour tenir compte de l'acc??l??ration subie par lui-m??me et les objets autour de lui. Un exemple, la force de pression le conducteur d'une voiture acc??l??rant dans son si??ge, a d??j?? ??t?? mentionn??; l'autre est la force que vous pouvez sentir tirant vos bras et si vous essayez de tourner comme une toupie. Ma??tre la perspicacit?? d'Einstein ??tait que la constante, traction famili??re du champ gravitationnel de la Terre est fondamentalement le m??me que ces forces fictives. La magnitude apparente des forces fictives semble toujours ??tre proportionnelle ?? la masse d'un objet sur lequel ils agissent - par exemple, le si??ge du conducteur exerce une force juste suffisante pour acc??l??rer le pilote ?? la m??me vitesse que la voiture. Par analogie, Einstein a propos?? qu'un objet dans un champ gravitationnel devrait se sentir une force gravitationnelle proportionnelle ?? sa masse, incarn??e dans La loi de la gravitation de Newton.
Cons??quences physiques
En 1907, Einstein ??tait encore huit ann??es loin de compl??ter la th??orie de la relativit?? g??n??rale. N??anmoins, il ??tait en mesure de faire un certain nombre de nouvelles pr??dictions testables, qui ??taient fond??es sur son point de d??part pour d??velopper sa nouvelle th??orie: le principe d'??quivalence.

Le premier effet est la nouvelle gravitationnelle d??calage de fr??quence de la lumi??re. Consid??rons deux observateurs bord d'une fus??e-navire acc??l??rer. ?? bord d'un tel navire, il ya un concept naturel de ??haut?? et ??bas??: la direction dans laquelle le bateau acc??l??re est "up", et les objets seules acc??l??rer dans la direction oppos??e, de tomber "vers le bas". Supposons que l'un des observateurs est "plus haut" que l'autre. Lorsque l'observateur inf??rieure envoie un signal lumineux ?? l'observateur plus, l'acc??l??ration fait que la lumi??re soit d??cal??e vers le rouge , qui peuvent ??tre calcul??es ?? partir de la relativit?? restreinte ; le deuxi??me observateur mesurer une faible la fr??quence de la lumi??re que la premi??re. Inversement, la lumi??re envoy??e ?? l'observateur sup??rieur ?? l'inf??rieur est d??cal??e vers le bleu, ce est d??cal??e vers des fr??quences plus ??lev??es. Einstein a fait valoir que ces d??calages de fr??quence doivent ??galement ??tre observ??es dans un champ gravitationnel. Ceci est illustr?? sur la figure de gauche, ce qui montre une onde lumineuse qui est progressivement d??cal??e vers le rouge comme il fait son chemin vers le haut contre l'acc??l??ration de la pesanteur. Cet effet a ??t?? confirm?? exp??rimentalement, comme d??crit ci-dessous .
Ce d??calage de fr??quence gravitationnelle correspond ?? une gravitationnelle dilatation du temps: Depuis l'observateur ??sup??rieur?? mesure la m??me onde lumineuse d'avoir une fr??quence inf??rieure ?? l'observateur ??inf??rieur??, le temps doit ??tre plus rapide pour passer l'observateur sup??rieur. Ainsi, le temps passe plus lentement pour les observateurs qui sont plus bas dans un champ gravitationnel.
Il est important de souligner que, pour chaque observateur, il n'y a pas de changements observables de l'??coulement du temps pour des ??v??nements ou des processus qui sont au repos dans son cadre de r??f??rence. Cinq minutes ??ufs que cadenc??e par l'horloge de chaque observateur ont la m??me consistance; jusqu'?? un an passe sur chaque horloge, chaque observateur ??ges de ce montant; chaque horloge, en bref, est en parfait accord avec l'ensemble des processus qui se passe dans son voisinage imm??diat. Ce est seulement lorsque les horloges sont compar??es entre observateurs distincts que l'on peut remarquer que le temps se plus lentement pour l'observateur inf??rieur pour le sup??rieur. Cet effet est infime, mais il a aussi ??t?? confirm??e exp??rimentalement dans de multiples exp??riences, comme d??crit ci-dessous .
De la m??me mani??re, Einstein pr??dit la d??viation gravitationnelle de la lumi??re: dans un champ gravitationnel, la lumi??re est d??vi?? vers le bas. Quantitativement, ses r??sultats ??taient outre par un facteur de deux; le bon calcul n??cessite une formulation plus compl??te de la th??orie de la relativit?? g??n??rale, et pas seulement le principe d'??quivalence.
Les effets de mar??e

L'??quivalence entre les effets gravitationnels et d'inertie ne constitue pas une th??orie compl??te de la gravit??. Quand il se agit d'expliquer la gravit?? pr??s de notre propre position sur la surface de la Terre, notant que notre cadre de r??f??rence ne est pas en chute libre, de sorte que forces fictives sont ?? pr??voir, fournit une explication appropri??e. Mais un cadre de r??f??rence en chute libre sur un c??t?? de la Terre ne peut pas expliquer pourquoi les gens sur le c??t?? oppos?? de la Terre ??prouvent une attraction gravitationnelle dans la direction oppos??e.
Une manifestation plus basique de la m??me effet implique deux corps qui tombent c??te ?? c??te vers la Terre. Dans un cadre de r??f??rence qui est en chute libre ?? c??t?? de ces corps, ils semblent flotter en apesanteur - mais pas exactement ainsi. Ces organismes ne sont pas en baisse dans exactement la m??me direction, mais vers un point dans l'espace: ?? savoir, de la Terre du centre de gravit?? . Par cons??quent, il est une composante du mouvement de chaque corps vers l'autre (voir la figure). Dans un petit environnement, comme un ascenseur en chute libre, cette acc??l??ration est minuscule par rapport, tandis que pour parachutistes sur les c??t??s oppos??s de la Terre, l'effet est grand. Ces diff??rences en vigueur sont ??galement responsables des mar??es dans les oc??ans de la Terre, de sorte que le terme " effet de mar??e ??est utilis?? pour ce ph??nom??ne.
L'??quivalence entre l'inertie et la gravit?? ne peut pas expliquer les effets de mar??e - il ne peut pas expliquer les variations dans le champ gravitationnel. Pour cela, il faut une th??orie qui d??crit la fa??on dont la mati??re (comme la grande masse de la Terre) affecte l'environnement d'inertie autour de lui.
De l'acc??l??ration ?? la g??om??trie
En explorant l'??quivalence de la gravit?? et l'acc??l??ration ainsi que le r??le des forces de mar??e, Einstein a d??couvert plusieurs analogies avec le g??om??trie de surfaces. Un exemple est la transition ?? partir d'un cadre de r??f??rence inertiel (dans lequel les particules libres c??te le long des sentiers droits ?? des vitesses constantes) ?? un cadre de r??f??rence de rotation (dans lequel les termes suppl??mentaires correspondant ?? forces fictives doivent ??tre mis en place afin d'expliquer le mouvement des particules): ce est analogue ?? la transition d'une cart??sienne Syst??me (dans lequel les lignes de coordonn??es sont des lignes droites) de coordonn??es ?? un syst??me (o?? les lignes de coordonn??es ne est pas n??cessairement lin??aire) courbes de coordonn??es.
Une analogie plus profonde concerne les forces de mar??e avec une propri??t?? de surfaces appel?? courbure. Pour les champs gravitationnels, l'absence ou la pr??sence de forces de mar??e d??termine si oui ou non l'influence de la gravit?? peut ??tre ??limin?? en choisissant un cadre de r??f??rence en chute libre. De m??me, l'absence ou la pr??sence de courbure d??termine si oui ou non une surface est ??quivalent ?? un plan . ?? l'??t?? de 1912, inspir?? par ces analogies, Einstein a cherch?? une formulation g??om??trique de gravit??.
Les objets ??l??mentaires de la g??om??trie - points, lignes , triangles - sont traditionnellement d??finis dans trois dimensions l'espace ou sur deux dimensions surfaces. En 1907, le math??maticien Hermann Minkowski (qui ??tait l'ancien professeur de math??matiques d'Einstein suisse polytechnique f??d??rale) a introduit une formulation g??om??trique d'Einstein th??orie de la relativit?? dans lequel la g??om??trie comprenait non seulement l'espace, mais aussi du temps. L'entit?? de base de cette nouvelle g??om??trie est quatre dimensions l'espace-temps. Les orbites des corps en mouvement sont les courbes dans l'espace-temps; les orbites des corps se d??pla??ant ?? une vitesse constante sans changer de direction correspondent ?? des lignes droites.
Pour les surfaces, la g??n??ralisation de la g??om??trie d'un plan - une surface plane - ?? celle d'une surface courbe g??n??rale a ??t?? d??crite au d??but du 19??me si??cle par Carl Friedrich Gauss . Cette description avait ?? son tour ??t?? g??n??ralis?? ?? des espaces de dimensions sup??rieures dans un formalisme math??matique introduit par Bernhard Riemann dans les ann??es 1850. Avec l'aide de La g??om??trie de Riemann, Einstein a formul?? une description g??om??trique de gravit?? dans lequel l'espace-temps de Minkowski est remplac?? par d??form??e, espace courbe, tout comme les surfaces courbes sont une g??n??ralisation des surfaces planes ordinaires.
Apr??s avoir r??alis?? la validit?? de cette analogie g??om??trique, il a fallu Einstein encore trois ans pour trouver la pierre angulaire manquante de sa th??orie: les ??quations d??crivant comment importance de la courbure de l'espace-temps influences. Ayant formul?? ce qui est maintenant connu sous le nom Les ??quations d'Einstein (ou, plus pr??cis??ment, ses ??quations du champ de gravit??), il a pr??sent?? sa nouvelle th??orie de la gravit?? lors de plusieurs sessions de la Acad??mie des sciences de Prusse ?? la fin de 1915.
G??om??trie et la gravitation
Paraphrasant John Wheeler, la th??orie g??om??trique de la gravitation d'Einstein peut se r??sumer ainsi: l'espace-temps dit importe comment se d??placer; question raconte comment l'espace-temps courbe. Ce que cela signifie est abord??e dans les trois sections suivantes, qui explorent le mouvement des particules dites essai, examiner les propri??t??s de la mati??re constituent une source de la gravit??, et, enfin, introduire les ??quations d'Einstein, qui concernent ces propri??t??s de la mati??re ?? la courbure l'espace-temps.
Sonder le champ gravitationnel

Afin de cartographier influence gravitationnelle d'un corps, il est utile de r??fl??chir ?? ce que les physiciens appellent sonde ou particules de test: des particules qui sont influenc??s par la gravit??, mais qui sont si petit et l??ger que nous pouvons n??gliger leur propre effet gravitationnel. En l'absence de gravit?? et d'autres forces ext??rieures, une particule de test se d??place le long d'une ligne droite ?? une vitesse constante. Dans la langue de l'espace-temps, ce qui est ??quivalent ?? dire que ces particules de test se d??placent le long droite lignes de monde dans l'espace-temps. En pr??sence de la gravit??, l'espace-temps est non-euclidienne, ou lignes courbes, et dans l'espace-temps courbes monde droites peuvent ne pas exister. Au lieu de cela, des particules de test se d??placent le long des lignes appel??es g??od??siques, qui sont "aussi droite que possible".
Une analogie simple est la suivante: En g??od??sie, la science de la mesure de la taille et la forme de la Terre, une g??od??sique (du grec "geo", la Terre, et "daiein", de diviser) est le plus court chemin entre deux points sur la surface de la Terre. Environ, une telle voie est une segment d'un grand cercle, tel qu'un ligne de longitude ou de l' ??quateur . Ces chemins sont certainement pas droit, tout simplement parce qu'ils doivent suivre la courbure de la surface de la Terre. Mais ils sont aussi droite que possible soumis ?? cette contrainte.
Les propri??t??s des g??od??siques diff??rent de celles des lignes droites. Par exemple, sur un plan, des lignes parall??les ne se rencontrent jamais, mais ce ne est pas le cas pour g??od??siques sur la surface de la Terre: par exemple, les lignes de longitude sont parall??les ?? l'??quateur, mais se croisent au niveau des p??les. De mani??re analogue, les lignes d'univers de particules d'essai sont en chute libre g??od??siques espace-temps, les lignes les plus droites possibles dans l'espace-temps. Mais il ya encore des diff??rences cruciales entre eux et les lignes droites vraiment qui peuvent ??tre trac??s dans le espace-temps sans gravit?? de la relativit?? restreinte. Dans la relativit?? restreinte, g??od??siques parall??les restent parall??les. Dans un champ gravitationnel avec des effets de mar??e, ce ne sera pas, en g??n??ral, ??tre le cas. Si, par exemple, deux corps sont initialement au repos par rapport ?? l'autre, mais sont ensuite d??pos??s dans le champ gravitationnel de la Terre, ils se d??placent vers l'autre comme ils tombent vers le centre de la Terre.
Compar?? avec les plan??tes et autres corps c??lestes, les objets de la vie quotidienne (personnes, voitures, maisons, m??me les montagnes) ont peu de masse. En ce qui concerne ces objets, les lois r??gissant le comportement des particules de test sont suffisants pour d??crire ce qui se passe. En particulier, afin de d??vier une particule de test ?? partir de sa trajectoire g??od??sique, une force ext??rieure doit ??tre appliqu??e. Une personne assise sur une chaise essaie de suivre une g??od??sique, ce est-?? tomber librement vers le centre de la Terre. Mais la pr??sidence applique une force externe vers le haut emp??chant la personne de tomber. De cette mani??re, la relativit?? g??n??rale explique l'exp??rience quotidienne de la gravit?? sur la surface de la terre vers le bas pas la traction d'une force de gravitation, mais comme la pouss??e vers le haut de forces ext??rieures. Ces forces d??vier tous les corps reposant sur la surface de la Terre depuis les g??od??siques qu'ils suivraient autrement. Pour les objets de mati??re dont l'influence gravitationnelle propre ne peut ??tre n??glig??, les lois du mouvement sont un peu plus compliqu?? que pour les particules de test, m??me se il reste vrai que l'espace-temps dit importe comment se d??placer.
Les ??quations d'Einstein
Les ??quations d'Einstein sont la pi??ce ma??tresse de la relativit?? g??n??rale. Ils fournissent une formulation pr??cise de la relation entre la g??om??trie de l'espace-temps et les propri??t??s de la mati??re, en utilisant le langage des math??matiques. Plus concr??tement, ils sont formul??s en utilisant les concepts de La g??om??trie de Riemann, dans lequel les propri??t??s g??om??triques d'un espace (ou un espace-temps) sont d??crits par une quantit?? appel??e m??trique. La m??trique code pour l'information n??cessaire pour calculer les notions g??om??triques fondamentales de la distance et de l'angle dans un espace courbe (ou espace-temps).

Une surface sph??rique comme celle de la Terre fournit un exemple simple. L'emplacement de tout point de la surface peut ??tre d??crit par deux coordonn??es: la g??ographique latitude et longitude. Contrairement aux coordonn??es cart??siennes de l'avion, coordonnent diff??rences ne sont pas les m??mes que les distances sur la surface, comme le montre le sch??ma de droite: pour quelqu'un ?? l'??quateur, d??pla??ant 30 degr??s de longitude ouest (ligne magenta) correspond ?? une distance de environ 3300 km (2100 mi). D'autre part, quelqu'un ?? une latitude de 55 degr??s, se d??pla??ant 30 degr??s de longitude ouest (ligne bleue) couvre une distance de seulement 1900 km (1200 mi). Donc coordonn??es ne fournissent pas suffisamment d'informations pour d??crire la g??om??trie d'une surface sph??rique, voire la g??om??trie de tout espace plus compliqu?? ou l'espace-temps. Cette information est pr??cis??ment ce qui est cod?? dans la m??trique, ce qui est une fonction d??finie ?? chaque point de la surface (ou l'espace, ou l'espace-temps) et se rapporte ?? coordonner les diff??rences diff??rences de distance. Toutes les autres quantit??s qui sont d'int??r??t pour la g??om??trie, tels que la longueur de ne importe quelle courbe donn??e, ou l'angle sous lequel deux courbes r??pondent, peuvent ??tre calcul??es ?? partir de cette fonction m??trique.
La fonction m??trique et son taux de variation d'un point ?? peuvent ??tre utilis??s pour d??finir une quantit?? g??om??trique appel?? Tenseur de Riemann, qui d??crit exactement comment l'espace (ou espace-temps) est incurv??e ?? chaque point. Dans la relativit?? g??n??rale, la m??trique et la courbure tenseur de Riemann sont des quantit??s d??finies ?? chaque point de l'espace-temps. Comme cela a d??j?? ??t?? mentionn??, la teneur en mati??re du l'espace-temps d??finit une autre quantit??, le Tenseur impulsion-??nergie T, et le principe que ??l'espace-temps dit importe comment se d??placer, l'espace-temps et de la mati??re raconte comment la courbe" signifie que ces quantit??s doivent ??tre li??s les uns aux autres. Einstein a formul?? cette relation en utilisant le tenseur de courbure de Riemann et la m??trique de d??finir une autre quantit?? g??om??trique G, maintenant appel?? le Tenseur d'Einstein, qui d??crit certains aspects de la fa??on dont l'espace-temps est courbe. L'??quation d'Einstein d??clare ensuite que
ce est ?? dire, jusqu'?? un multiple constant, la quantit?? G (qui mesure la courbure) est assimil?? ?? la quantit?? T (qui mesure la teneur en mati??re). Les constantes impliqu??es dans cette ??quation refl??tent les diff??rentes th??ories qui ont servi ?? sa fabrication: π est une des constantes de base de la g??om??trie, G est le constante gravitationnelle qui est d??j?? pr??sent dans la gravitation newtonienne, et c est la vitesse de la lumi??re , la constante cl?? dans la relativit?? restreinte.
Cette ??quation est souvent appel?? au pluriel comme les ??quations d'Einstein, puisque les quantit??s G et T sont chacun d??termin??s par plusieurs fonctions des coordonn??es de l'espace-temps, et les ??quations assimiler chacune de ces fonctions composants. Une solution de ces ??quations d??crivant une g??om??trie particuli??re de espace et le temps; par exemple, la Solution de Schwarzschild d??crit la g??om??trie autour, une masse non rotative sph??rique comme une ??toile ou d'un trou noir , alors que le Solution de Kerr d??crit un trou noir en rotation. D'autres solutions peuvent toujours d??crire une onde gravitationnelle ou, dans le cas de la Friedmann-Lema??tre solution-Robertson-Walker, un univers en expansion. La solution la plus simple est la non courb??e Minkowski l'espace-temps, l'espace-temps d??crite par la relativit?? restreinte.
Des essais exp??rimentaux
Aucune th??orie scientifique est apodictiquement vrai; chacun est un mod??le qui doit ??tre v??rifi?? par l'exp??rience. La loi de la gravitation de Newton a ??t?? accept??e, car elle repr??sentait le mouvement des plan??tes et des lunes dans le syst??me solaire avec une grande pr??cision. Comme la pr??cision des mesures exp??rimentales progressivement am??lior??s, certains ??carts avec les pr??visions de Newton ont ??t?? observ??s, et ceux-ci ont ??t?? prises en compte dans la th??orie de la relativit?? g??n??rale. De m??me, les pr??dictions de la relativit?? g??n??rale doivent ??galement ??tre v??rifi??s avec l'exp??rience, et Einstein lui-m??me mis au point trois tests maintenant connu comme les tests classiques de la th??orie:

- Gravit?? newtonien pr??dit que le orbite une seule plan??te autour d'une trace parfaitement sph??rique ??toiles devrait ??tre une ellipse . La th??orie d'Einstein pr??dit une courbe plus complexe: la plan??te se comporte comme si elle ??tait en voyage autour d'une ellipse, mais en m??me temps, l'ellipse dans son ensemble tourne lentement autour de l'??toile. Dans le sch??ma de droite, l'ellipse pr??dite par la gravitation newtonienne est affich??e en rouge, et une partie de l'orbite pr??dite par Einstein en bleu. Pour une plan??te en orbite autour du Soleil, cette d??viation ?? partir des orbites de Newton est connu comme le anormale passage au p??rih??lie. La premi??re mesure de cet effet, pour la plan??te Mercure , remonte ?? 1859. Les r??sultats les plus pr??cis pour le mercure et d'autres plan??tes ?? ce jour sont bas??es sur des mesures qui ont ??t?? men??es entre 1966 et 1990, en utilisant des radiot??lescopes . La relativit?? g??n??rale pr??dit le passage au p??rih??lie anormale correcte pour toutes les plan??tes o?? cela peut ??tre mesur??e avec pr??cision ( Mercure , V??nus et de la Terre ).
- Selon la relativit?? g??n??rale, la lumi??re ne se d??place pas en ligne droite quand il se propage dans un champ gravitationnel. Au lieu de cela, il est d??vi?? en pr??sence de corps massifs. En particulier, la lumi??re des ??toiles est d??vi?? de son passage pr??s du Soleil, conduit ?? des changements apparents de jusqu'?? 1,75 secondes d'arc dans les positions des ??toiles dans le ciel de nuit (une seconde d'arc est ??gal ?? 1/3600 d'un degr?? ). Dans le cadre de la gravitation newtonienne, un argument heuristique peut ??tre faite qui m??ne ?? la d??viation de la lumi??re par la moiti?? de ce montant. Les diff??rentes pr??dictions peuvent ??tre test??es en observant les ??toiles qui sont pr??s du Soleil pendant une ??clipse solaire . De cette fa??on, une exp??dition britannique ?? l'Afrique de l'Ouest en 1919, dirig?? par Arthur Eddington, a confirm?? que la pr??diction d'Einstein ??tait correcte, et les pr??dictions newtoniens mal, par l'observation de la Mai 1919 ??clipse. Les r??sultats de Eddington ne ??taient pas tr??s pr??cis; observations ult??rieures de la d??viation de la lumi??re du lointain quasars par le soleil, qui utilisent des techniques tr??s pr??cises de radioastronomie, ont confirm?? les r??sultats de Eddington avec beaucoup plus de pr??cision (la premi??re de ces mesures datent de 1967, la plus r??cente analyse compl??te ?? partir de 2004).
- Redshift gravitationnel a ??t?? mesur??e la premi??re fois dans un laboratoire en 1959 par Pound et Rebka. On le voit ??galement dans les mesures astrophysiques, notamment pour la lumi??re se ??chappant du White Dwarf Sirius B . La connexes gravitationnelle effet de la dilatation du temps a ??t?? mesur??e en transportant horloges atomiques ?? des altitudes entre des dizaines et des dizaines de milliers de kilom??tres (d'abord par Hafele et Keating en 1971; plus de pr??cision ?? ce jour par Gravity Probe A lanc?? en 1976).
De ces tests, seul le avance du p??rih??lie de Mercure ??tait connu avant la publication finale d'Einstein de la relativit?? g??n??rale en 1916. La confirmation exp??rimentale subs??quente de ses autres pr??dictions, en particulier les premi??res mesures de la d??viation de la lumi??re par le soleil en 1919, catapult?? Einstein pour la c??l??brit?? internationale. Ces trois essais exp??rimentaux ont justifi?? l'adoption de la relativit?? g??n??rale sur la th??orie de Newton et, accessoirement, sur un certain nombre de alternatives ?? la relativit?? g??n??rale qui avaient ??t?? propos??s.

D'autres tests de la relativit?? g??n??rale comprennent des mesures de pr??cision de la Effet Shapiro ou de retard de temps gravitationnelle de la lumi??re, le plus r??cemment en 2002 par le Cassini sonde spatiale. Une s??rie de tests se concentre sur les effets pr??vus par la relativit?? g??n??rale pour le comportement de gyroscopes voyageant ?? travers l'espace. L'un de ces effets, pr??cession g??od??sique, a ??t?? test?? avec le R??flecteur lunaire (des mesures de haute pr??cision de l'orbite de la Lune ). Un autre, qui est li?? ?? des masses en rotation, est appel??e frame-glisser. Les effets g??od??siques et ch??ssis-glisser ont tous deux ??t?? test??s par le Gravity Probe B exp??rience satellite lanc?? en 2004, avec des r??sultats confirmant la relativit?? ?? 0,5% et 15%, respectivement, en D??cembre 2008.
En normes cosmiques, la gravit?? dans le syst??me solaire est faible. Depuis les diff??rences entre les pr??dictions d'Einstein et les th??ories de Newton sont plus prononc??s lorsque la gravit?? est forte, les physiciens se int??ressent depuis longtemps ?? tester diff??rents effets relativistes dans un cadre avec relativement forts champs gravitationnels. Cela est devenu possible gr??ce ?? des observations de pr??cision de pulsars binaires. Dans un tel syst??me d'??toiles, deux tr??s compact ??toiles ?? neutrons en orbite autour de l'autre. Au moins l'un d'eux est un pulsar - un objet astronomique qui ??met un faisceau ??troit d'ondes radio. Ces faisceaux frappent la Terre ?? intervalles tr??s r??guliers, de fa??on similaire ?? la fa??on dont le faisceau tournant d'un phare signifie qu'un observateur voit un clin phare, et peut ??tre observ?? comme une s??rie tr??s r??guli??re d'impulsions. La relativit?? g??n??rale pr??dit d??viations sp??cifiques de la r??gularit?? de ces impulsions radio. Par exemple, ?? des moments o?? les ondes radio passent pr??s de l'autre ??toile ?? neutrons, ils doivent ??tre d??vi??s par le champ gravitationnel de l'??toile. Les s??quences d'impulsions observ??es sont remarquablement proches de ceux pr??dits par la relativit?? g??n??rale.
Un ensemble particulier d'observations est li??e ?? des applications pratiques ??minemment utiles, ?? savoir syst??mes de navigation par satellite comme le Syst??me de positionnement mondial qui sont utilis??s ?? la fois pour pr??cise positionnement et chronom??trage. De tels syst??mes se appuient sur deux ensembles de horloges atomiques: les horloges ?? bord des satellites en orbite de la Terre, et horloges de r??f??rence stationn??es sur la surface de la Terre. La relativit?? g??n??rale pr??dit que ces deux ensembles d'horloges doivent cocher ?? des taux l??g??rement diff??rents, en raison de leurs diff??rents mouvements (un effet d??j?? pr??dit par la relativit?? restreinte) et leurs diff??rentes positions dans le champ gravitationnel de la Terre. Afin d'assurer la pr??cision du syst??me, les horloges des satellites sont soit ralentis par un facteur relativiste, ou m??me facteur est faite partie de l'algorithme d'??valuation. ?? leur tour, les tests de la pr??cision du syst??me (en particulier les mesures tr??s approfondies qui font partie de la d??finition de universel coordonn?? heure) t??moignent de la validit?? des pr??dictions relativistes.
Un certain nombre d'autres tests ont explor?? la validit?? de diff??rentes versions de la Principe d'Equivalence; ?? proprement parler, toutes les mesures de gravit?? dilatation du temps sont des tests de la version faible de ce principe, pas de la relativit?? g??n??rale elle-m??me. Jusqu'?? pr??sent, la relativit?? g??n??rale a pass?? tous les tests d'observation.
Applications astrophysiques
Les mod??les fond??s sur la relativit?? g??n??rale jouent un r??le important dans l'astrophysique , et le succ??s de ces mod??les est une preuve suppl??mentaire de la validit?? de la th??orie.
Lentille gravitationnelle

Puisque la lumi??re est d??vi??e dans un champ gravitationnel, il est possible pour la lumi??re d'un objet ??loign?? pour atteindre un observateur le long de deux ou plusieurs chemins. Par exemple, la lumi??re d'un objet tr??s lointain comme un quasar peut passer le long d'un c??t?? d'une immense galaxie et ??tre d??vi?? l??g??rement de mani??re ?? atteindre un observateur sur la Terre, tandis que la lumi??re passant le long du c??t?? oppos?? de cette m??me galaxie est d??vi?? ainsi, atteindre le m??me observateur d'une direction l??g??rement diff??rente. En cons??quence, cet observateur particulier verra un objet astronomique ?? deux endroits diff??rents dans le ciel de nuit. Ce genre de focalisation est bien connu quand il se agit de lentilles optiques, et donc l'effet gravitationnel correspondant est appel?? lentille gravitationnelle.
Astronomie observationnelle utilise des effets lenticulaires comme un outil important pour d??duire les propri??t??s de l'objet de lentille. M??me dans les cas o?? cet objet ne est pas directement visible, la forme d'une image ?? lentille fournit des informations sur la masse de distribution responsable de la d??viation de la lumi??re. En particulier, lentille gravitationnelle fournit une fa??on de mesurer la distribution de la mati??re noire , qui ne donne pas de lumi??re et peut ??tre observ??e que par ses effets gravitationnels. Une application particuli??rement int??ressante sont des observations ?? grande ??chelle, o?? les masses lenticulaires sont r??partis sur une fraction importante de l'univers observable, et peut ??tre utilis?? pour obtenir des informations sur les propri??t??s de grande envergure et de l'??volution de notre cosmos.
Les ondes gravitationnelles
Les ondes gravitationnelles, une cons??quence directe de la th??orie d'Einstein, sont des distorsions de la g??om??trie qui se propagent ?? la vitesse de la lumi??re, et peuvent ??tre consid??r??s comme des ondulations dans l'espace-temps. Ils ne doivent pas ??tre confondus avec le ondes de gravit?? de la dynamique des fluides, qui sont un concept diff??rent.
Indirectement, l'effet des ondes gravitationnelles a ??t?? d??tect?? dans les observations d'??toiles binaires sp??cifiques. Ces paires d'??toiles l'orbite de l'autre et, comme ils le font, peu à peu perdre de l'énergie en émettant des ondes gravitationnelles. Pour les étoiles ordinaires comme notre soleil, cette perte d'énergie serait trop faible pour être détectable, mais cette perte d'énergie a été observée en 1974 dans un pulsar binaire appelé PSR1913 + 16. Dans un tel système, l'une des étoiles en orbite autour d'un pulsar est. Cela a deux conséquences: un pulsar est un objet extrêmement dense connu comme un étoile à neutrons, pour lesquels l'émission d'ondes gravitationnelles est beaucoup plus forte que pour les étoiles ordinaires. En outre, un pulsar émet un faisceau étroit de rayonnement électromagnétique à partir de ses pôles magnétiques. Lors de la rotation des pulsars, ses balayages de faisceau sur la Terre, où il est considéré comme une série régulière d'impulsions radio, tout comme un navire en mer observe clignote réguliers de lumière provenant de la rotation dans un phare. Ce motif régulier de la radio impulsions fonctionne comme une "horloge" très précis. Il peut être utilisé pour chronométrer la période orbitale de l'étoile double, et il réagit de manière sensible à des distorsions de l'espace-temps dans son voisinage immédiat.
Les d??couvreurs de PSR1913 + 16, Russell Hulse et Joseph Taylor, ont reçu le prix Nobel de physique en 1993. Depuis lors, plusieurs autres pulsars binaires ont été trouvées. Les plus utiles sont ceux dans lesquels les deux étoiles sont pulsars, car ils fournissent les tests les plus précis de la relativité générale.
Actuellement, un objectif majeur de la recherche dans la relativité est la détection directe des ondes gravitationnelles. À cette fin, un certain nombre de terrestres détecteurs d'ondes gravitationnelles sont en opération, et une mission de lancer un détecteur spatial, LISA, est actuellement en cours de développement, avec une mission de précurseur ( LISA Pathfinder) dont le lancement en Juin 2013. Si les ondes gravitationnelles sont détectés, ils pourraient être utilisés pour obtenir des informations sur les objets compacts tels que les étoiles à neutrons et les trous noirs , et aussi de sonder l'état du début des univers fractions de seconde après le Big Bang .
Trous noirs

Lorsque la masse est concentrée dans une suffisamment région compacte de l'espace, la relativité générale prédit la formation d'un trou noir - une région de l'espace avec une attraction gravitationnelle si forte que même la lumière ne peut échapper. Certains types de trous noirs sont pensés pour être l'état final dans l' évolution de massives étoiles . D'autre part, trous noirs supermassifs avec la masse de millions, voire des milliards de Soleils sont supposés résider dans les noyaux de la plupart des galaxies , et ils jouent un rôle clé dans actuelle modèles de comment les galaxies se sont formées au cours des derniers milliards d'années.
Matière tombant sur ??????un objet compact est l'un des mécanismes les plus efficaces pour libérer l'énergie sous forme de rayonnement et de la matière tombant sur ??????les trous noirs est pensé pour être responsable de certains des plus brillants phénomènes astronomiques imaginables. Parmi les exemples notables de grand intérêt pour les astronomes sont les quasars et les autres types de noyaux actifs de galaxies. Dans de bonnes conditions, la chute des matières accumulant autour d'un trou noir peut conduire à la formation de jets, dans lequel les faisceaux de matière sont axés jeté loin dans l'espace à des vitesses proches de celle de la lumière .
Il ya plusieurs propriétés qui en font la plupart des trous noirs sources prometteuses d'ondes gravitationnelles. Une des raisons est que les trous noirs sont les objets les plus compacts qui peuvent orbite de l'autre dans le cadre d'un système binaire; en conséquence, les ondes gravitationnelles émises par un tel système sont particulièrement fortes. Une autre raison découle de ce que l'on appelle trou noir théorèmes d'unicité: au fil du temps, les trous noirs conservent seulement un ensemble minimal de caractéristiques distinctives (depuis différents styles de cheveux sont une partie cruciale de ce qui donne des personnes différentes de leurs différentes apparences, ces théorèmes sont devenus connus comme " pas de cheveux "théorèmes). Par exemple, dans le long terme, l'effondrement d'une question hypothétique cube ne se traduira pas dans un trou noir en forme de cube. Au lieu de cela, le trou noir résultant sera indiscernable d'un trou noir formé par l'effondrement d'une masse sphérique, mais avec une différence importante: dans sa transition vers une forme sphérique, le trou noir formé par l'effondrement d'un cube émet des ondes gravitationnelles .
Cosmologie

Un des aspects les plus importants de la relativité générale est qu'il peut être appliqué à l' univers dans son ensemble. Un point clé est que, sur de grandes échelles, notre univers semble être construit le long des lignes très simples: toutes les observations actuelles suggèrent que, en moyenne, la structure du cosmos devrait être approximativement le même, quel que soit l'emplacement ou la direction de l'observation d'un observateur : l'univers est d'environ homog??ne et isotrope. Ces univers relativement simples peuvent être décrits par de simples solutions de l'équation d'Einstein. Les actuels modèles cosmologiques de l'univers sont obtenus en combinant ces solutions simples à la relativité générale avec les théories décrivant les propriétés de l'univers de la matière de contenu, à savoir la thermodynamique , au nucléaire et la physique des particules . Selon ces modèles, notre univers actuel a émergé d'un état ??????à haute température extrêmement dense (le Big Bang ) environ 14 milliard il ya des années, et a été en pleine expansion depuis.
Les équations d'Einstein peut être généralisées en ajoutant un terme appelé constante cosmologique. Lorsque ce terme est présent, l'espace vide lui-même agit comme une source de attrayant ou, exceptionnellement, gravité répulsive. Einstein introduit à l'origine ce terme dans son travail de pionnier sur la cosmologie papier 1917, avec une motivation très spécifique: la pensée cosmologique contemporaine tenu l'univers d'être statique, et le terme supplémentaire a été nécessaire pour construire des univers de modèles statiques dans le cadre de la relativité générale. Quand il est devenu évident que l'univers est pas statique, mais en expansion, Einstein n'a pas tardé à se débarrasser de ce terme supplémentaire; prématurément, comme nous le savons aujourd'hui: Depuis environ 1998, sur un corps d'accumuler progressivement des éléments de preuve astronomique a montré que l'expansion de l'univers est l'accélération d'une manière qui suggère la présence d'une constante cosmologique ou, de façon équivalente, d'une énergie sombre avec spécifique propriétés qui imprègne tout l'espace.
La recherche moderne: la relativité générale et au-delà
La relativité générale est très réussi à fournir un cadre pour des modèles précis qui décrivent un éventail impressionnant de phénomènes physiques. D'autre part, il ya beaucoup de questions ouvertes intéressants, et en particulier, la théorie dans son ensemble est presque certainement incomplète.
Contrairement à toutes les autres théories modernes de interactions fondamentales, la relativité générale est une théorie classique: il ne comprend pas les effets de la physique quantique . La quête pour une version quantique de la relativité générale aborde l'un des plus fondamentaux des questions ouvertes en physique. Bien qu'il existe des candidats prometteurs pour une telle théorie de la gravité quantique, notamment la théorie des cordes et gravité quantique à boucles, il est à l'heure actuelle aucune théorie cohérente et complète. Il a longtemps été espéré qu'une théorie de la gravité quantique permettrait aussi d'éliminer un autre aspect problématique de la relativité générale: la présence de singularités de l'espace-temps. Ces singularités sont à laquelle la géométrie devient mal défini, avec la conséquence que la relativité générale elle-même perd son pouvoir prédictif des frontières («bords tranchants») de l'espace-temps. En outre, il ya ce qu'on appelle des théorèmes de singularité qui prédisent que ces singularités doivent existent au sein de l'univers, si les lois de la relativité générale devaient tenir sans aucune modification quantiques. Les exemples les plus connus sont les singularités associées avec les univers de modèles qui décrivent les trous noirs et le début de l'univers .
D'autres tentatives pour modifier la relativité générale ont été faites dans le cadre de la cosmologie . Dans les modèles cosmologiques modernes, plus d'énergie dans l'univers est dans les formes qui ont jamais été détectées directement, à savoir l'énergie noire et matière noire . Il ya eu plusieurs propositions controversées Pour obvier à la nécessité de ces formes énigmatiques de matière et d'énergie, en modifiant les lois régissant la gravité et la dynamique de l'expansion cosmique, par exemple la dynamique newtonienne modifiée.
Au-delà des défis d'effets quantiques et de la cosmologie, la recherche sur la relativité générale est riche de possibilités pour une exploration plus poussée: relativistes mathématiques explorent la nature des singularités et les propriétés fondamentales des équations d'Einstein, des simulations informatiques de plus en plus complets de spacetimes spécifiques (tels que ceux fusion décrivant trous noirs) sont exécutés, et la course pour la première détection directe des ondes gravitationnelles continuent de plus belle. Plus de quatre vingt dix ans après la théorie a d'abord été publié, la recherche est plus actif que jamais.