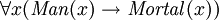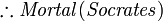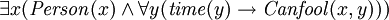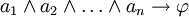Logique du premier ordre
Saviez-vous ...
SOS Enfants, un organisme de bienfaisance de l'??ducation , a organis?? cette s??lection. enfants SOS est le plus grand don de charit?? du monde enfants orphelins et abandonn??s la chance de la vie familiale.
Logique du premier ordre (FOL) est un formelle syst??me d??ductif utilis?? par les math??maticiens, des philosophes, des linguistes et des informaticiens. Il va par beaucoup de noms, y compris: premier ordre calcul des pr??dicats (FOPC), le calcul des pr??dicats inf??rieure, le langage de la logique du premier ordre ou de la logique des pr??dicats. Contrairement langues naturelles telles que l'anglais, FOL utilise un d??pourvue de toute ambigu??t?? langage formel interpr??t?? par des structures math??matiques. FOL est un syst??me de d??duction ??tendant logique propositionnelle en permettant la quantification sur des individus d'un domaine donn?? (univers) du discours. Par exemple, il peut ??tre indiqu?? dans FOL "Chaque individu a la propri??t?? P".
Bien que logique propositionnelle traite des propositions d??claratives simples, logiques de premier ordre plus couvertures pr??dicats et la quantification. Prenez par exemple les phrases suivantes: "Socrate est un homme??, ??Platon est un homme". Dans la logique propositionnelle ces deux propositions seront ind??pendants, d??sign??s par exemple par p et q. Dans la logique du premier ordre cependant, les deux peines seraient reli??s par la m??me propri??t??: Man (x), o?? l'Homme (x) signifie que x est un homme. Lorsque x = Socrate nous obtenons la premi??re proposition, p, et quand x = Platon nous obtenons la seconde proposition, q. Une telle construction permet une logique beaucoup plus puissant quand quantificateurs sont introduits, tels que "pour tout x ...", par exemple, "pour tout x, si l'Homme (x), alors ...". Sans quantificateurs, chaque argument valable dans FOL est valable dans la logique propositionnelle, et vice versa.
Une th??orie du premier ordre se compose d'un ensemble de axiomes (g??n??ralement fini ou r??cursivement ??num??rable) et les ??tats d??ductible de leur donner la relation de d??ductibilit?? sous-jacent. Habituellement ce qu'on entend par ??th??orie du premier ordre?? est un certain ensemble d'axiomes ainsi que ceux d'un (et le son) axiomatisation compl??te de la logique du premier ordre, ferm?? en vertu des r??gles de FOL. (Tout syst??me FOL donnera lieu ?? la m??me relation de d??ductibilit?? abstraite, donc nous ne avons pas besoin d'un syst??me axiomatique fixe ?? l'esprit.) Un langage du premier ordre a le pouvoir expressif suffisante pour officialiser deux th??ories math??matiques importantes: ZFC la th??orie des ensembles et Arithm??tique de Peano. Un langage du premier ordre ne peut pas, cependant, exprimer cat??goriquement la notion de responsabilisation, m??me si elle est exprimable dans la th??orie du premier ordre sous la ZFC interpr??tation voulue pour le symbolisme de ZFC. Ces id??es peuvent ??tre exprim??es avec cat??goriquement logique du second ordre.
Pourquoi logique du premier ordre est n??cessaire?
Logique propositionnelle ne est pas ad??quat pour formaliser des arguments valables qui se appuient sur la structure interne des propositions concern??es. Pour le voir, examiner la validit?? l'argument syllogistique:
- Tous les hommes sont mortels
- Socrate est un homme
- Par cons??quent, Socrate est mortel
qui, lors de la traduction en propositionnel rendements logiques:
- Un
- B
 C
C
(Prise  pour signifier ??donc??).
pour signifier ??donc??).
Selon la logique propositionnelle, cette traduction ne est pas valide: logique propositionnelle valide arguments selon leur structure, et rien dans la structure de cet argument traduit (C r??sulte de A et B, pour arbitraire A, B, C) sugg??re qu'il est valide. Une traduction qui pr??serve la validit?? intuitive (et formelle) de l'argument doit prendre en consid??ration la structure profonde de propositions, tels que les notions essentielles de la pr??dication et la quantification. Logique propositionnelle ne traite que de la v??rit?? fonctionnelle validit??: toute cession de valeurs de v??rit?? aux variables de l'argument devrait soit la conclusion vrai ou au moins l'une des pr??misses fausses. Il est clair que nous pouvons (uniforme) attribuer des valeurs de v??rit?? aux variables de l'argument ci-dessus tel que A, B sont ?? la fois vrai, mais c est faux. D'o?? l'argument est la v??rit?? fonctionnellement invalide. D'autre part, il est impossible de (uniforme) attribuer des valeurs de v??rit?? ?? l'argument "Un d??coule de (A et B)" telle que (A et B) est vraie (d'o?? A est vrai et B est vrai) et un faux .
En revanche, cet argument peut ??tre facilement traduit en logique du premier ordre:
(O?? "  "Signifie" pour tout x ","
"Signifie" pour tout x ","  "Signifie" implique ",
"Signifie" implique ",  signifie ??Socrate est un homme??, et
signifie ??Socrate est un homme??, et  signifie ??Socrate est mortel??.) En clair, cela indique que
signifie ??Socrate est mortel??.) En clair, cela indique que
- pour tout x, si x est un homme alors x est mortel
- Socrate est un homme
- donc Socrate est mortel
FOL peut ??galement exprimer l'existence de quelque chose ( 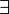 ), Ainsi que des pr??dicats (??fonctions?? qui sont vrai ou faux) avec plus d'un param??tre. Par exemple, "il ya quelqu'un qui peut ??tre dupe chaque fois" peut ??tre exprim??e comme suit:
), Ainsi que des pr??dicats (??fonctions?? qui sont vrai ou faux) avec plus d'un param??tre. Par exemple, "il ya quelqu'un qui peut ??tre dupe chaque fois" peut ??tre exprim??e comme suit:
Lorsque " 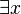 ??Signifie?? il existe (e) x ","
??Signifie?? il existe (e) x ","  ??Signifie?? et ??, et
??Signifie?? et ??, et  moyens "(personne) x peut ??tre dupe (au moment) y".
moyens "(personne) x peut ??tre dupe (au moment) y".
D??finition premier ordre logique
Un calcul des pr??dicats se compose de
- r??gles de formation (c. D??finitions r??cursives pour former formules bien form??).
- r??gles de transformation (c.-??- r??gles d'inf??rence pour d??river th??or??mes).
- axiomes ou axiome sch??mas (??ventuellement infini d??nombrable).
Les axiomes consid??r??s ici sont axiomes logiques qui font partie de FOL classique. Il est important de noter que FOL peut ??tre formalis?? dans de nombreuses mani??res ??quivalentes; il n'y a rien canonique sur les axiomes et les r??gles d'inf??rence fournies dans cet article. Il ya une infinit?? de formalisations ??quivalentes tous qui donnent les m??mes th??or??mes et les non-th??or??mes, et qui ont tous un droit ??gal vers le titre ??FOL??.
FOL est utilis?? comme "bloc de construction" de base pour de nombreuses th??ories math??matiques. FOL propose plusieurs r??gles int??gr??es, telles que l'axiome 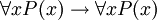 (Si P (x) est vraie pour tout x alors P (x) est vraie pour tout x). Axiomes non-logiques suppl??mentaires sont ajout??s pour produire th??ories de premier ordre sp??cifiques bas??s sur les axiomes de la FOL classique; ces th??ories construites sur FOL sont appel??s th??ories classiques de premier ordre. Un exemple d'une th??orie du premier ordre classique est Arithm??tique de Peano, qui ajoute l'axiome
(Si P (x) est vraie pour tout x alors P (x) est vraie pour tout x). Axiomes non-logiques suppl??mentaires sont ajout??s pour produire th??ories de premier ordre sp??cifiques bas??s sur les axiomes de la FOL classique; ces th??ories construites sur FOL sont appel??s th??ories classiques de premier ordre. Un exemple d'une th??orie du premier ordre classique est Arithm??tique de Peano, qui ajoute l'axiome 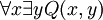 (Ce est ?? dire pour tout x il existe y tel que y = x + 1, o?? Q (x, y) est interpr??t??e comme "y = x + 1"). Cet axiome suppl??mentaire est un axiome non-logique; il ne est pas partie de FOL, mais est un axiome de la th??orie (un axiome de l'arithm??tique plut??t que de la logique). Axiomes de ce dernier type sont ??galement appel??s axiomes de th??ories de premier ordre. Les axiomes de th??ories de premier ordre ne sont pas consid??r??s comme des v??rit??s de la logique en soi, mais plut??t comme des v??rit??s de la th??orie particuli??re qui a g??n??ralement associ?? ?? une interpr??tation pr??vue de ses symboles non logiques. (Voir une id??e analogue ?? logique par rapport symboles non-logique.) Ainsi, l'axiome ?? propos de Q (x, y) ne est vrai que l'interpr??tation de la relation Q (x, y) comme ??y = x + 1", et seulement dans la th??orie de Arithm??tique de Peano. FOL classique ne ont associ?? ?? une interpr??tation destin??e de son vocabulaire non-logique (sauf sans doute un symbole d??signant l'identit??, selon que l'on consid??re un tel symbole que logique). classique th??orie des ensembles est un autre exemple d'une th??orie du premier ordre (une th??orie construite sur FOL).
(Ce est ?? dire pour tout x il existe y tel que y = x + 1, o?? Q (x, y) est interpr??t??e comme "y = x + 1"). Cet axiome suppl??mentaire est un axiome non-logique; il ne est pas partie de FOL, mais est un axiome de la th??orie (un axiome de l'arithm??tique plut??t que de la logique). Axiomes de ce dernier type sont ??galement appel??s axiomes de th??ories de premier ordre. Les axiomes de th??ories de premier ordre ne sont pas consid??r??s comme des v??rit??s de la logique en soi, mais plut??t comme des v??rit??s de la th??orie particuli??re qui a g??n??ralement associ?? ?? une interpr??tation pr??vue de ses symboles non logiques. (Voir une id??e analogue ?? logique par rapport symboles non-logique.) Ainsi, l'axiome ?? propos de Q (x, y) ne est vrai que l'interpr??tation de la relation Q (x, y) comme ??y = x + 1", et seulement dans la th??orie de Arithm??tique de Peano. FOL classique ne ont associ?? ?? une interpr??tation destin??e de son vocabulaire non-logique (sauf sans doute un symbole d??signant l'identit??, selon que l'on consid??re un tel symbole que logique). classique th??orie des ensembles est un autre exemple d'une th??orie du premier ordre (une th??orie construite sur FOL).
Vocabulaire
Avant mise en place des r??gles de formation, il faut d??crire la "vocabulaire", qui se compose de
- Un ensemble de variables sous-jacentes (ou relations) chacun avec une certaine valence (ou arit??, nombre de ses arguments) ≥1, qui sont souvent d??sign??s par des lettres majuscules P, Q, R, ....
- Par exemple, P (x) est un pr??dicat variables de valence 1. Il peut se tenir pour "x est un homme", par exemple.
- Q (x, y) est un pr??dicat variables de valence 2. Il peut se tenir pour "x est sup??rieur ?? y" en arithm??tique ou "x est le p??re de y", par exemple.
- Il est possible de permettre aux relations de valence 0; ceux-ci peuvent ??tre consid??r??es comme variables propositionnelles. Par exemple, P, qui peut se tenir pour toute d??claration.
- En utilisant les fonctions (voir ci-dessous), il est possible de se passer de toutes les variables sous-jacentes avec valence sup??rieur ?? un. Par exemple, "x> y?? (un pr??dicat de valence 2, du type Q (x, y)) peuvent ??tre remplac??s par un pr??dicat de valence 1 ?? propos de la couple (x, y).
- Un ensemble de constantes, souvent d??sign?? par les lettres minuscules au d??but de l'alphabet a, b, c, ....
- Exemples: un peut tenir pour Socrates. En arithm??tique , il peut se pr??senter ?? 0. En th??orie des ensembles , un tel constante peut tenir pour le ensemble vide.
- Un ensemble de fonctions, chacune d'un certain valence ≥ 1, qui sont souvent d??sign??e par les lettres minuscules f, g, h, ....
- Exemples: f (x) peuvent se pr??senter "le p??re de x". En arithm??tique , on peut tenir pour "-x". En th??orie des ensembles , il peut signifier ??la ensemble des x de puissance ". En arithm??tique , f (x, y) peut signifier ??x + y". En th??orie des ensembles , il peut se pr??senter ?? ??l'union de x et y".
- Une constante est vraiment une fonction de valence 0. Cependant il est de tradition d'utiliser le terme ??fonction?? que pour des fonctions de valence au moins une.
- On peut en principe renoncer enti??rement aux fonctions d'arit??> 2 et pr??dicats d'arit??> 1 se il est un symbole de fonction d'arit?? 2 repr??sentant un paire ordonn??e (ou symboles de pr??dicat d'arit?? 2 repr??sentant les relations de projection d'un paire ordonn??e). La paire ou projections doivent satisfaire les axiomes naturels.
- On peut en principe renoncer enti??rement aux fonctions et constantes. Par exemple, au lieu d'utiliser une constante 0, on peut utiliser un pr??dicat 0 (x) (interpr??t?? comme "x = 0"), et de remplacer chaque pr??dicat tel que P (0, y)
 x 0 (x)
x 0 (x)  P (x, y). Une fonction telle que f (x1, x2 ...) comportera aussi ??tre remplac?? par un pr??dicat F (x1, x2 ..., y) (interpr??t?? comme "y = f (x1, x2 ...)").
P (x, y). Une fonction telle que f (x1, x2 ...) comportera aussi ??tre remplac?? par un pr??dicat F (x1, x2 ..., y) (interpr??t?? comme "y = f (x1, x2 ...)").
- Un ensemble infini de variables, souvent d??sign?? par les lettres minuscules ?? la fin de l'alphabet x, y, z, ....
- Symboles d??signant les op??rateurs logiques (ou connecteurs):
 ( logique de ne pas),
( logique de ne pas),  ( conditionnelle logique).
( conditionnelle logique).  (Φ
(Φ 
 ψ) est logiquement ??quivalente ?? φ
ψ) est logiquement ??quivalente ?? φ  ψ ( et logique). φ
ψ ( et logique). φ  ψ peut ??tre consid??r?? comme un raccourci pour cela. Alternativement, on peut ajouter le
ψ peut ??tre consid??r?? comme un raccourci pour cela. Alternativement, on peut ajouter le  symbole comme un op??rateur logique au vocabulaire et axiomes appropri??s.
symbole comme un op??rateur logique au vocabulaire et axiomes appropri??s.  φ
φ  ψ est logiquement ??quivalente ?? φ
ψ est logiquement ??quivalente ?? φ 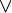 ψ ( ou logique). φ
ψ ( ou logique). φ 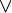 ψ peut ??tre consid??r?? comme un raccourci pour cela. Alternativement, on peut ajouter le
ψ peut ??tre consid??r?? comme un raccourci pour cela. Alternativement, on peut ajouter le 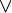 symbole comme un op??rateur logique au vocabulaire et axiomes appropri??s.
symbole comme un op??rateur logique au vocabulaire et axiomes appropri??s. - De m??me, (φ
 ψ)
ψ)  (Ψ
(Ψ  φ) est logiquement ??quivalente ?? φ
φ) est logiquement ??quivalente ?? φ 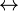 ψ ( biconditional logique), et l'on peut utiliser ce dernier comme un raccourci pour cela, ou encore ajouter ceci ?? le vocabulaire et ajouter axiomes appropri??s. Parfois φ
ψ ( biconditional logique), et l'on peut utiliser ce dernier comme un raccourci pour cela, ou encore ajouter ceci ?? le vocabulaire et ajouter axiomes appropri??s. Parfois φ 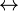 ψ est ??crit que φ
ψ est ??crit que φ  ψ.
ψ.
- Symboles indiquant quantificateurs:
 ( quantification universelle, g??n??ralement lire comme ??pour tous??).
( quantification universelle, g??n??ralement lire comme ??pour tous??). 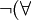 x
x  φ) est logiquement ??quivalent ??
φ) est logiquement ??quivalent ?? 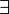 x φ ( quantification existentielle, g??n??ralement lire comme "il existe"). Ce dernier peut soit ??tre utilis?? comme un raccourci pour cela, ou ajout?? au vocabulaire avec axiomes appropri??s.
x φ ( quantification existentielle, g??n??ralement lire comme "il existe"). Ce dernier peut soit ??tre utilis?? comme un raccourci pour cela, ou ajout?? au vocabulaire avec axiomes appropri??s.
- Gauche et parenth??se droite.
- Il existe de nombreuses conventions diff??rentes sur o?? mettre entre parenth??ses; par exemple, on pourrait ??crire
 ou x (
ou x (  x). Parfois, on utilise deux points ou des arr??ts complets au lieu de parenth??ses pour faire formules sans ambigu??t??. Une convention int??ressante, mais est plut??t inhabituel " Notation polonaise ", o?? l'on omet tous les parenth??ses, et ??crit
x). Parfois, on utilise deux points ou des arr??ts complets au lieu de parenth??ses pour faire formules sans ambigu??t??. Une convention int??ressante, mais est plut??t inhabituel " Notation polonaise ", o?? l'on omet tous les parenth??ses, et ??crit  ,
,  Et ainsi de suite devant leurs arguments non entre eux. Notation polonaise est compact et ??l??gant, mais rare parce qu'il est difficile pour les humains de le lire.
Et ainsi de suite devant leurs arguments non entre eux. Notation polonaise est compact et ??l??gant, mais rare parce qu'il est difficile pour les humains de le lire.
- Il existe de nombreuses conventions diff??rentes sur o?? mettre entre parenth??ses; par exemple, on pourrait ??crire
- Un symbole de l'identit?? ou de l'??galit?? = est parfois, mais pas toujours inclus dans le vocabulaire.
- Si l'??galit?? est consid??r??e comme une partie de la logique du premier ordre, le symbole de l'??galit?? comporte syntaxiquement comme un pr??dicat binaire. Ce cas est parfois appel?? logique du premier ordre avec ??galit??.
Il existe plusieurs autres variations mineures dans la liste ci-dessous:
- L'ensemble des symboles primitifs (op??rateurs et quantificateurs) varie souvent. Il est possible d'inclure d'autres op??rateurs primitifs, tels que
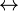 (FIF),
(FIF),  (B) et
(B) et  (Ou), la v??rit?? constantes T pour "true" et F pour "false" (ce sont les op??rateurs de valence 0), et / ou de la Sheffer course (P | Q, alias NAND). Le nombre minimum de symboles primitifs n??cessaires est une, mais si nous nous limitons aux op??rateurs ??num??r??s ci-dessus, nous avons besoin de trois, comme ci-dessus.
(Ou), la v??rit?? constantes T pour "true" et F pour "false" (ce sont les op??rateurs de valence 0), et / ou de la Sheffer course (P | Q, alias NAND). Le nombre minimum de symboles primitifs n??cessaires est une, mais si nous nous limitons aux op??rateurs ??num??r??s ci-dessus, nous avons besoin de trois, comme ci-dessus. - Certains livres et papiers utilisent φ de notation
 ψ pour φ
ψ pour φ  ψ. Cela est particuli??rement vrai en th??orie preuve lorsque
ψ. Cela est particuli??rement vrai en th??orie preuve lorsque  est facilement confondu avec la fl??che de s??quent. On voit aussi ~ φ pour
est facilement confondu avec la fl??che de s??quent. On voit aussi ~ φ pour  φ, φ et ψ pour φ
φ, φ et ψ pour φ  ψ, et une richesse de notations pour quantificateurs; par exemple,
ψ, et une richesse de notations pour quantificateurs; par exemple,  x φ peut se ??crire (x) φ. Cette derni??re annotation est commun dans les textes sur la th??orie de la r??cursivit??.
x φ peut se ??crire (x) φ. Cette derni??re annotation est commun dans les textes sur la th??orie de la r??cursivit??. - Il est souvent plus facile dans la pratique d'utiliser une notation simple qui prend en charge les op??rateurs infixes et omet parenth??ses inutiles. Ainsi, si P est une relation de valence 2, nous ??crivons souvent ??P ab" "P b" au lieu de; par exemple, nous ??crivons une <2 au lieu de <(1 2). De m??me, si f est une fonction de valence 2, nous ??crivons parfois "AFB" au lieu de "f (ab)"; par exemple, nous ??crivons 1 + 2 au lieu de + (1 2). Par convention, les op??rateurs infixes ont tendance ?? utiliser des noms de fonction non alphab??tiques. Il est ??galement courant d'omettre certains parenth??ses si cela ne conduit pas ?? l'ambigu??t?? (conduisant ?? la d??finition d'une priorit??).
- Il est parfois utile de dire que "P (x) est v??rifi??e pour exactement une x", qui peut ??tre exprim?? sous la forme
 x P (x). Cette notation ne peut ??tre prise pour abr??ger une formule telle que
x P (x). Cette notation ne peut ??tre prise pour abr??ger une formule telle que  x (P (x)
x (P (x)  y (P (y)
y (P (y)  (X = y))).
(X = y))).
Les programmes informatiques qui acceptent de premier ordre repr??sentations logiques seront g??n??ralement accepter au moins ces quantificateurs et les op??rateurs (m??me se ils peuvent utiliser diff??rents symboles pour les repr??senter):  (Pour tous),
(Pour tous), 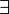 (Existe),
(Existe),  (Non),
(Non),  (Et),
(Et), 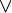 (Ou),
(Ou),  (Implique), et
(Implique), et 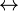 (Si et seulement si). Le exclusif ou l'exploitant "XOR" est ??galement fr??quente.
(Si et seulement si). Le exclusif ou l'exploitant "XOR" est ??galement fr??quente.
Les ensembles de constantes, les fonctions et les relations sont normalement consid??r??s comme formant une langue, tandis que les variables, les op??rateurs logiques, et quantificateurs sont g??n??ralement consid??r??s comme appartenant ?? la logique. Par exemple, le langage de la th??orie de groupe se compose d'une constante (l'??l??ment d'identit??), une fonction de valence 1 (l'inverse) une fonction de valence 2 (le produit), et une relation de valence 2 (??galit??), qui serait omis par des auteurs qui incluent l'??galit?? dans la logique sous-jacente.
r??gles de Formation
Les r??gles de formation d??finissent les termes et formules de logique du premier ordre. Lorsque termes et formules sont repr??sent??es comme des cha??nes de symboles, ces r??gles peuvent ??tre utilis??es pour ??crire un grammaire formelle pour les termes et formules. Le concept de variable libre est utilis?? pour d??finir des phrases en tant que sous-ensemble des formules.
Termes
L'ensemble des termes est r??cursive d??finies par les r??gles suivantes:
- Toute constante est un terme.
- Toute variable est un terme.
- Toute expression f (t 1, ..., t n) de n ≥ 1 arguments (o?? chaque argument t i est un terme et f est un symbole de fonction de valence n) est un terme.
- clause de Fermeture: Rien d'autre ne est un terme. Par exemple, les pr??dicats sont pas des termes.
Formules
L'ensemble des formules bien form??es (g??n??ralement appel??s s WFF ou tout simplement formules) est r??cursive d??finies par les r??gles suivantes:
- Pr??dicats simples et complexes Si P est une relation de valence n ≥ 1 et les a i sont des termes alors p (a 1, ..., a n) est bien form??. Si l'??galit?? est consid??r??e comme faisant partie de la logique, alors (a 1 = 2) est bien form??e. Toutes ces formules sont dites atomique.
- Clause inductif I: Si φ est une wff, puis
 φ est un wff.
φ est un wff. - Clause inductif II: Si φ et ψ sont s WFF, alors (φ
 ψ) est une wff.
ψ) est une wff. - Clause inductive III: Si φ est une wff et x est une variable,
 x φ est un wff.
x φ est un wff. - Fermeture article: Rien d'autre ne est un wff.
Par exemple,  x
x  y (P (f (x))
y (P (f (x)) 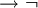 (P (x)
(P (x)  Q (f (y), x, z))) est une formule bien form??, si f est une fonction de valence 1, P un pr??dicat de valence 1 et Q un pr??dicat de valence 3.
Q (f (y), x, z))) est une formule bien form??, si f est une fonction de valence 1, P un pr??dicat de valence 1 et Q un pr??dicat de valence 3.  xx
xx  ne est pas une formule bien form??e.
ne est pas une formule bien form??e.
Dans la science informatique terminologie, une formule impl??mente un type "bool??en" int??gr??, tandis qu'un terme met en ??uvre tous les autres types.
Variables libres et li??s
- Formules atomiques Si φ est une formule atomique alors X est libre dans φ si et seulement si x se produit dans φ.
- Inductif article I: x est libre dans
 φ si et seulement si x est libre dans φ.
φ si et seulement si x est libre dans φ. - Clause inductif II: x est libre dans (φ
 ψ) si et seulement si x est libre dans φ et ne se produit pas dans ψ, ou x est libre dans ψ et ne se produit pas dans φ, ou x est libre ?? la fois φ et ψ.
ψ) si et seulement si x est libre dans φ et ne se produit pas dans ψ, ou x est libre dans ψ et ne se produit pas dans φ, ou x est libre ?? la fois φ et ψ. - Clause inductive III: x est libre dans
 y φ si et seulement si x est libre dans φ et x est un symbole diff??rent de y.
y φ si et seulement si x est libre dans φ et x est un symbole diff??rent de y. - Fermeture article: x est li?? dans φ si et seulement si x se produit dans φ et x ne est pas libre dans φ.
- Par exemple, dans
 x
x  y (P (x)
y (P (x)  Q (x, f (x), z) de variables), X et Y sont li??s, z est une variable libre, et w ne est pas, car il ne se produit pas dans la formule.
Q (x, f (x), z) de variables), X et Y sont li??s, z est une variable libre, et w ne est pas, car il ne se produit pas dans la formule.
Exemple
En math??matiques la langue de groupes ab??liens ordonn??s a une constante 0, une fonction unaire -, une fonction binaire +, et une relation binaire ≤. Donc:
- 0, x, y sont des termes atomiques
- + (X, y) + (x, + (y, - (z))) sont termes, habituellement ??crit x + y, x + y - z
- = (+ (X, y), 0) ≤ (+ (x, + (y, - (z))) + (x, y)) sont des formules atomiques, habituellement ??crit comme x + y = 0, x Y + - z ≤ x + y,
- (
 x
x  y ≤ (+ (x, y), z))
y ≤ (+ (x, y), z))  (
(  x = (+ (x, y), 0)) est une formule, g??n??ralement ??crit comme (
x = (+ (x, y), 0)) est une formule, g??n??ralement ??crit comme (  x
x  y x + y ≤ z)
y x + y ≤ z)  (
(  x x + y = 0).
x x + y = 0).
Substitution
Si t est un terme et φ (x) est une formule contenant ??ventuellement des x en tant que variable libre, puis φ (t) est d??fini comme ??tant le r??sultat de remplacer toutes les occurrences libres de x par t, ?? condition que pas variable libre de t devient li?? ?? ce processus. Si une variable libre de t est li??, puis t remplacer x il est d'abord n??cessaire de changer les noms des variables li??es de φ ?? autre chose que les variables libres de t.
Pour voir pourquoi cette condition est n??cessaire, envisager la formule φ (x) donn??e par  y y x ≤ ("x est maximale??). Si t est un terme sans y comme une variable libre, alors φ (t) signifie simplement t est maximale. Cependant, si t est l'y φ de formule (y) est
y y x ≤ ("x est maximale??). Si t est un terme sans y comme une variable libre, alors φ (t) signifie simplement t est maximale. Cependant, si t est l'y φ de formule (y) est  y y ≤ y qui ne dit pas que y est maximale. Le probl??me est que la variable y libre de t (= y) est devenu li?? quand nous avons substitu?? pour Y x dans φ (x). Donc, pour φ (y) former nous devons d'abord changer la variable li??e y de φ ?? autre chose, dire z, de sorte que φ (y) est alors
y y ≤ y qui ne dit pas que y est maximale. Le probl??me est que la variable y libre de t (= y) est devenu li?? quand nous avons substitu?? pour Y x dans φ (x). Donc, pour φ (y) former nous devons d'abord changer la variable li??e y de φ ?? autre chose, dire z, de sorte que φ (y) est alors  z z ≤ y. Oubliant cette condition est une cause notoire d'erreurs.
z z ≤ y. Oubliant cette condition est une cause notoire d'erreurs.
Les r??gles d'inf??rence
Une r??gle d'inf??rence est une fonction ?? partir d'ensembles de (bien form??s) formules, appel?? locaux, ?? des ensembles de formules appel??es conclusions. Dans les syst??mes d??ductifs les plus connus, les r??gles d'inf??rence prennent un ensemble de formules ?? une seule conclusion. (Notez que ce est vrai m??me dans le cas de la plupart s??quent calculs.)
Les r??gles d'inf??rence sont utilis??es pour prouver des th??or??mes , qui sont prouvables en mati??re de formules ou des membres d'une th??orie. Si le locaux d'une r??gle d'inf??rence sont des th??or??mes, sa conclusion est un th??or??me ainsi. En d'autres termes, les r??gles d'inf??rence sont utilis??es pour g??n??rer des ??nouveaux?? th??or??mes de ??anciens?? - ils sont theoremhood pr??servent. Syst??mes pour les th??ories de g??n??ration sont souvent appel??s calculs jacentes. Elles sont d??crites dans une section ci-dessous.
Une r??gle d'inf??rence importante, modus ponens, stipule que si φ et φ  ψ sont deux th??or??mes, alors ψ est un th??or??me. Ceci peut se ??crire de la mani??re suivante;
ψ sont deux th??or??mes, alors ψ est un th??or??me. Ceci peut se ??crire de la mani??re suivante;
- si
 et
et 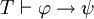 , Puis
, Puis 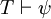
o??  indique
indique  est prouvable en th??orie T. Il existe des syst??mes d??ductifs (connus sous le nom Hilbert-style syst??mes d??ductifs) dans lequel modus ponens est la seule r??gle d'inf??rence; dans de tels syst??mes, l'absence d'autres r??gles d'inf??rence est compens??e avec une abondance de r??gimes d'axiomes logiques.
est prouvable en th??orie T. Il existe des syst??mes d??ductifs (connus sous le nom Hilbert-style syst??mes d??ductifs) dans lequel modus ponens est la seule r??gle d'inf??rence; dans de tels syst??mes, l'absence d'autres r??gles d'inf??rence est compens??e avec une abondance de r??gimes d'axiomes logiques.
Une deuxi??me r??gle d'inf??rence est importante G??n??ralisation universelle. On peut affirmer que
- si
 , Puis
, Puis 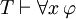
Qui se lit: si φ est un th??or??me, puis "pour tout x, φ" est un th??or??me ainsi. Le sch??ma d'aspect semblable 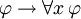 ne est pas saine, en g??n??ral, m??me si elle ne dispose cependant instances valides, comme lorsque x ne est pas libre dans φ (voir G??n??ralisation (logique)).
ne est pas saine, en g??n??ral, m??me si elle ne dispose cependant instances valides, comme lorsque x ne est pas libre dans φ (voir G??n??ralisation (logique)).
Axiomes
Ici suit une description des axiomes de la logique du premier ordre. Comme expliqu?? ci-dessus, une th??orie donn??e de premier ordre, a d'autres axiomes non-logiques. Les axiomes logiques suivants caract??risent un calcul des pr??dicats pour l'exemple de cet article de la logique du premier ordre.
Pour une quelconque th??orie, il est int??ressant de savoir si l'ensemble des axiomes peut ??tre g??n??r?? par un algorithme, ou se il existe un algorithme qui d??termine si une formule bien form??e est un axiome.
Se il ya un algorithme pour g??n??rer tous les axiomes, alors l'ensemble des axiomes est dit r??cursivement ??num??rable.
Se il est un algorithme qui d??termine apr??s un nombre fini d'??tapes si une formule est un axiome ou non, alors l'ensemble des axiomes est dit r??cursif ou d??cidable. Dans ce cas, on peut aussi construire un algorithme pour g??n??rer tous les axiomes: cet algorithme se appuie tout simplement toutes les formules possibles un par un (d'une longueur de plus en plus), et pour chaque formule l'algorithme d??termine si ce est un axiome.
Axiomes de la logique du premier ordre sont toujours d??cidable. Cependant, dans une th??orie du premier ordre axiomes non-logiques ne sont pas n??cessairement tel.
axiomes de quantificateurs
axiomes de quantificateurs changent en fonction de la fa??on dont le vocabulaire est d??fini, comment la proc??dure de remplacement fonctionne, quelles sont les r??gles de formation et dont les r??gles d'inf??rence sont utilis??s. Ici suit un exemple pr??cis de ces axiomes
- PRED-1:

- PRED-2:
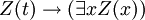
- PRED-3:

- PRED-4:
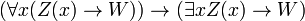
Ce sont en fait axiome sch??mas: l'expression W repr??sente tout wff dans laquelle x ne est pas libre, et l'expression Z (x) signifie toute wff ?? la convention additionnelle que Z (t) repr??sente le r??sultat de la substitution du terme t pour x dans Z (x). Ainsi, ce est un ensemble r??cursif d'axiomes.
Un autre axiome, 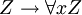 , Pour Z dans laquelle x ne se produit pas, est parfois ajout??.
, Pour Z dans laquelle x ne se produit pas, est parfois ajout??.
Egalit?? et ses axiomes
Il existe plusieurs conventions diff??rentes pour l'utilisation de l'??galit?? (ou l'identit??) dans la logique du premier ordre. Cette section r??sume les principales. Les diff??rentes conventions donnent tous essentiellement les m??mes r??sultats avec environ la m??me quantit?? de travail, et diff??rent principalement dans la terminologie.
- La convention la plus courante pour l'??galit?? est d'inclure le symbole de l'??galit?? comme un symbole logique primitive, et ajouter les axiomes pour l'??galit?? aux axiomes de la logique du premier ordre. Les axiomes d'??galit?? sont
- x = x
- x = y → f (..., x, ...) = f (..., y, ...) pour toute fonction f
- x = y → (P (..., x, ...) → P (..., y, ...)) pour toute relation P (y compris la relation d'??galit?? elle-m??me)
- Ce sont, aussi, axiome sch??mas: ils d??finissent un algorithme qui d??cide si une formule donn??e est un axiome. Ainsi, ce est un ensemble r??cursif d'axiomes.
- La prochaine convention la plus courante consiste ?? inclure le symbole de l'??galit?? comme une des relations d'une th??orie, et ajouter les axiomes d'??galit?? aux axiomes de la th??orie. En pratique, cela est presque impossible ?? distinguer de la convention pr??c??dente, sauf dans le cas inhabituel de th??ories sans notion d'??galit??. Les axiomes sont les m??mes, et la seule diff??rence est que l'on appelle certains d'entre eux axiomes ou axiomes de la th??orie logiques.
- Dans les th??ories sans fonctions et un nombre fini de relations, il est possible de d??finir l'??galit?? en termes de relations, en d??finissant les deux termes s et t d'??tre ??gaux si toute relation est inchang??e en changeant s ?? t dans ne importe quel argument.
- Par exemple, dans la th??orie des ensembles avec une relation
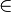 , Nous pouvons d??finir s = t ??tre une abr??viation pour
, Nous pouvons d??finir s = t ??tre une abr??viation pour  x (s
x (s 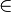 x
x 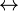 t
t 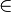 x)
x) 
 x (x
x (x  s
s  x
x  t). Cette d??finition de l'??galit?? satisfait alors automatiquement les axiomes pour l'??galit??.
t). Cette d??finition de l'??galit?? satisfait alors automatiquement les axiomes pour l'??galit??. - Sinon, si l'on ne utilise le symbole de l'??galit?? comme une relation de la th??orie ou de la logique, il faudrait alors ajouter des axiomes. Dans l'exemple pr??c??dent, il faudrait ajouter l'axiome
 s
s  t (
t (  x (x
x (x  s
s 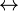 x
x 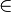 t))
t))  s = t.
s = t.
- Par exemple, dans la th??orie des ensembles avec une relation
- Dans certaines th??ories, il est possible de donner des d??finitions ad hoc de l'??galit??. Par exemple, dans une th??orie des ordres partiels avec une relation ≤ nous pourrions d??finir s = t ??tre une abr??viation pour s ≤ t
 t ≤ s.
t ≤ s.
Calcul des pr??dicats
Le calcul des pr??dicats est une bonne extension de la calcul propositionnel, qui d??termine les d??clarations de la logique du premier ordre sont d??montrables. Un grand nombre (mais pas tous) th??ories math??matiques peuvent ??tre formul??es dans le calcul des pr??dicats. Si le calcul propositionnel est d??finie par un ensemble appropri?? d'axiomes et de la r??gle unique de l'inf??rence modus ponens (ce qui peut ??tre fait de plusieurs fa??ons), puis le calcul des pr??dicats peuvent ??tre d??finies en ajoutant le calcul des propositions de plusieurs axiomes et de la r??gle d'inf??rence appel??e ??g??n??ralisation universelle". Comme axiomes pour le calcul des pr??dicats nous prenons:
- Tous les tautologies du calcul des propositions, prises sch??matiquement sorte que le remplacement uniforme d'une lettre par une formule sch??matique est autoris??.
- Les axiomes de quantificateurs, donn??s ci-dessus.
- Les axiomes ci-dessus pour l'??galit??, si l'??galit?? est consid??r??e comme un concept logique.
Une phrase est d??fini pour ??tre prouvable en logique du premier ordre se il peut ??tre d??duit des axiomes du calcul des pr??dicats, en appliquant de fa??on r??p??t??e les r??gles d'inf??rence "modus de Ponens?? et ??g??n??ralisation universelle". Autrement dit:
- Un axiome du calcul des pr??dicats est prouvable en logique du premier ordre par d??finition.
- Si le locaux d'une r??gle d'inf??rence sont prouvable en logique du premier ordre, alors il en est de son conclusion.
Si nous avons une th??orie T (un ensemble d'??nonc??s, appel??s axiomes, dans une langue) alors φ de phrase est d??fini pour ??tre prouvable dans la th??orie T si
est prouvable en logique du premier ordre, pour un certain ensemble fini d'axiomes  de la th??orie T. En d'autres termes, si l'on peut prouver dans la logique du premier ordre φ d??coule des axiomes de T. Cela signifie aussi que l'on remplace la proc??dure ci-dessus pour trouver des phrases prouvables par la suivante:
de la th??orie T. En d'autres termes, si l'on peut prouver dans la logique du premier ordre φ d??coule des axiomes de T. Cela signifie aussi que l'on remplace la proc??dure ci-dessus pour trouver des phrases prouvables par la suivante:
- Un axiome de T est prouvable dans T.
- Un axiome du calcul des pr??dicats est prouvable dans T.
- Si le locaux d'une r??gle d'inf??rence sont prouvable dans T, alors il en est de son conclusion.
Un probl??me apparent avec cette d??finition de prouvabilit?? est qu'il semble plut??t ad hoc: nous avons pris un certain collection apparemment al??atoire d'axiomes et de r??gles d'inf??rence, et il ne est pas clair que nous ne avons pas accidentellement manqu?? quelque axiome ou une r??gle essentielle. Th??or??me de compl??tude de G??del nous assure que ce ne est pas vraiment un probl??me: tout ??nonc?? vrai dans tous les mod??les (s??mantiquement vrais) est prouvable en logique du premier ordre (syntaxiquement vrai). En particulier, toute d??finition raisonnable de "prouvable" dans la logique du premier ordre doit ??tre ??quivalent ?? celui ci-dessus (se il est possible pour les longueurs d'??preuves diff??rent consid??rablement pour diff??rentes d??finitions de prouvabilit??).
Il ya plusieurs fa??ons diff??rentes (mais ??quivalents) pour d??finir prouvabilit??. La d??finition ci-dessus est typique pour un calcul "de style Hilbert", qui a de nombreux axiomes, mais tr??s peu de r??gles d'inf??rence. En revanche, un ??Style Gentzen" calcul des pr??dicats a quelques axiomes mais beaucoup de r??gles d'inf??rence.
Identit??s prouvables
Les phrases suivantes peuvent ??tre appel??es ??identit??s?? parce que le conjonctif dans chaque principale est la biconditional. Ils sont tous prouvable en FOL, et sont utiles lors de la manipulation des quantificateurs:
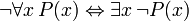

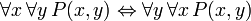
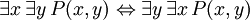


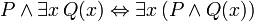 (O??
(O??  ne doit pas se produire gratuitement
ne doit pas se produire gratuitement  )
)  (O??
(O??  ne doit pas se produire gratuitement
ne doit pas se produire gratuitement  )
)
R??gles d'inf??rence prouvables
Le principal conjonctif dans les phrases suivantes, aussi prouvable en FOL, est le conditionnelle. Ces peines peuvent ??tre consid??r??s comme la justification de r??gles d'inf??rence en plus modus ponens et la g??n??ralisation universelle discut??s ci-dessus et dont la validit??:
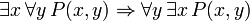
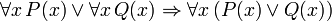
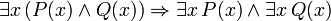
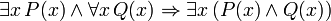
 (Si c est une variable, alors il ne doit pas ??tre quantifi?? pr??c??demment dans P (x))
(Si c est une variable, alors il ne doit pas ??tre quantifi?? pr??c??demment dans P (x)) 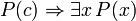 (Il doit y avoir aucune instance libre de x dans P (c))
(Il doit y avoir aucune instance libre de x dans P (c))
Th??or??mes m??talogiques de logique du premier ordre
Certains th??or??mes m??talogiques importants sont list??s ci-dessous sous forme puces. Ce qu'ils veulent dire ?? peu pr??s, ce est que la peine est valide si et seulement si elle est prouvable. En outre, on peut construire un algorithme qui fonctionne comme suit: si une phrase est prouvable, l'algorithme va nous dire que, dans une quantit?? finie, mais de temps inconnue. Si une phrase est ind??montrable, l'algorithme fonctionnera toujours, et nous ne saurons pas si la peine est ind??montrable ou d??montrable et l'algorithme que nous a tout simplement pas encore dit. Un tel algorithme est appel?? semidecidable ou r??cursivement ??num??rable.
On peut construire un algorithme qui va d??terminer en nombre fini d'??tapes si une peine est prouvable (un algorithme d??cidable) que pour les classes simples de la logique du premier ordre.
- Le probl??me de d??cision pour la validit?? est r??cursivement ??num??rable; en d'autres termes, il existe un Machine de Turing que lorsque donn?? aucune phrase comme entr??e, se arr??te si et seulement si la phrase est valable (vrai dans tous les mod??les).
- Comme Exhaustivit?? th??or??me de G??del les spectacles, pour toute formule valide P, P est prouvable. Inversement, en supposant que la coh??rence de la logique, toute formule d??montrable est valide.
- La machine de Turing peut ??tre un compos?? qui g??n??re toutes les formules d??montrables de la mani??re suivante: pour un fini ou r??cursive ensemble d??nombrable d'axiomes, une telle machine peut ??tre celui qui g??n??re un axiome, puis g??n??re une nouvelle formule prouvable par l'application d'axiomes et de r??gles d'inf??rence d??j?? g??n??r??s, puis g??n??rer un autre axiome, et ainsi de suite. Compte tenu d'une phrase comme entr??e, la machine de Turing aller simplement sur et g??n??re toutes les formules prouvables un par un, et se arr??te si elle g??n??re la phrase.
- Contrairement ?? la la logique propositionnelle, la logique du premier ordre est ind??cidable, ?? condition que la langue a au moins un pr??dicat de valence au moins deux autres que l'??galit??. Cela signifie qu'il n'y a pas proc??dure de d??cision qui d??termine correctement si une formule arbitraire est valide. Parce qu'il est une machine de Turing comme d??crit ci-dessus, le ind??cidabilit?? est li?? ?? l'insolubilit?? de la Probl??me de l'arr??t: existe pas d'algorithme qui d??termine apr??s un nombre fini d'??tapes si la machine de Turing sera jamais halte pour une phrase donn??e en entr??e, par cons??quent, si la phrase est prouvable. Ce r??sultat a ??t?? ??tabli ind??pendamment par ??glise et Turing .
- La logique des pr??dicats Monadique (c.-??-logique des pr??dicats avec seulement un argument de pr??dicats et pas de fonctions) est d??cidable.
- Le Classe Bernays-Sch??nfinkel de formules du premier ordre est ??galement d??cidable.
Traduire langage naturel ?? la logique du premier ordre
Concepts exprim??es en langage naturel doivent ??tre ??traduits?? ?? la logique du premier ordre (FOL) avant FOL peut ??tre utilis?? pour y faire face, et il ya un certain nombre de pi??ges potentiels dans cette traduction. Dans FOL, 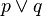 signifie "p, ou q, ou les deux", autrement dit, il est inclus. En anglais, le mot ??ou?? est parfois inclus (par exemple, "la cr??me ou de sucre???), Mais il est parfois exclusive (par exemple, "caf?? ou de th???" Est g??n??ralement destin?? ?? signifier un ou l'autre, pas les deux). De m??me, le mot anglais ??certains?? peut signifier ??au moins un, peut-??tre tous", mais d'autres fois, cela peut signifier "pas tous, peut-??tre pas". Le mot anglais "et" doit parfois ??tre traduit par "ou" (par exemple, "les hommes et les femmes peuvent se appliquer").
signifie "p, ou q, ou les deux", autrement dit, il est inclus. En anglais, le mot ??ou?? est parfois inclus (par exemple, "la cr??me ou de sucre???), Mais il est parfois exclusive (par exemple, "caf?? ou de th???" Est g??n??ralement destin?? ?? signifier un ou l'autre, pas les deux). De m??me, le mot anglais ??certains?? peut signifier ??au moins un, peut-??tre tous", mais d'autres fois, cela peut signifier "pas tous, peut-??tre pas". Le mot anglais "et" doit parfois ??tre traduit par "ou" (par exemple, "les hommes et les femmes peuvent se appliquer").
Limitations de la logique du premier ordre
Toutes les notations math??matiques ont leurs forces et leurs faiblesses;voici quelques ces questions avec la logique du premier ordre.
Difficulté représentant if-then-else
Curieusement, FOL avec l'égalité (comme généralement défini) ne comprend ni ne permet la définition d'un if-then-else prédicat ou une fonction si (c, a, b), où "c" est une condition exprimé en une formule, alors a et b sont soit les deux termes ou les deux formules, et son résultat serait "une" si c est vrai, et "b" si elle est fausse. Le problème est que dans FOL, deux prédicats et fonctions ne peuvent accepter les termes («non-booléens») en tant que paramètres, mais la représentation «évidente» de l'état est une formule ("booléen"). Cela est regrettable, car beaucoup de fonctions mathématiques sont commodément exprimées en termes de si-alors-sinon, et si-alors-sinon est fondamentale pour décrire la plupart des programmes informatiques.
Mathématiquement, il est possible de redéfinir un ensemble complet de nouvelles fonctions répondant aux opérateurs de la formule, mais cela est assez maladroite. Un prédicat si (c, a, b) peut être exprimée dans FOL se réécrit sous la forme 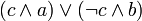 , mais cela est maladroite si la condition c est complexe. Beaucoup étendent FOL pour ajouter un prédicat cas spécial nommé "if (condition, a, b)" (où a et b sont des formules) et / ou de la fonction "ite (état, a, b)" (où a et b sont des termes ), qui tous deux accepter une formule comme la condition, et sont égaux à "a" si la condition est vraie et "b" si elle est fausse. Ces extensions font FOL plus facile à utiliser pour certains problèmes, et de faire certains types d'automatique théorème prouvant facile. D'autres l'étendent FOL davantage afin que les fonctions et prédicats peuvent accepter les deux termes et formules à toute position.
, mais cela est maladroite si la condition c est complexe. Beaucoup étendent FOL pour ajouter un prédicat cas spécial nommé "if (condition, a, b)" (où a et b sont des formules) et / ou de la fonction "ite (état, a, b)" (où a et b sont des termes ), qui tous deux accepter une formule comme la condition, et sont égaux à "a" si la condition est vraie et "b" si elle est fausse. Ces extensions font FOL plus facile à utiliser pour certains problèmes, et de faire certains types d'automatique théorème prouvant facile. D'autres l'étendent FOL davantage afin que les fonctions et prédicats peuvent accepter les deux termes et formules à toute position.
Typing (Sorts)
FOL ne comprend pas les types (sortes) dans la notation elle-même, autres que la différence entre les formules ("booléens") et des termes («non-booléens"). Certains affirment que ce manque de types est un grand avantage, mais beaucoup d'autres trouvent des avantages dans la définition et l'utilisation de types (sortes), comme aider les rejeter certaines spécifications erronées ou indésirables. Ceux qui souhaitent indiquer types doivent fournir ces informations en utilisant la notation disponible dans FOL. Cela peut faire de telles expressions plus complexes, et peut également être facile de se tromper.
Prédicats seul paramètre peuvent être utilisés pour mettre en ??uvre la notion de types le cas échéant. Par exemple, dans: 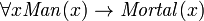 , le prédicat
, le prédicat  peut être considéré comme une sorte de "Type affirmation" (qui est, qui
peut être considéré comme une sorte de "Type affirmation" (qui est, qui  doit être un homme). Prédicats peut également être utilisé avec le "existe" quantifier pour identifier les types, mais cela devrait normalement être fait avec l'opérateur "et" à la place, par exemple:
doit être un homme). Prédicats peut également être utilisé avec le "existe" quantifier pour identifier les types, mais cela devrait normalement être fait avec l'opérateur "et" à la place, par exemple: 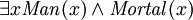 ("il existe quelque chose qui est à la fois un homme et est mortel"). Il est facile d'écrire
("il existe quelque chose qui est à la fois un homme et est mortel"). Il est facile d'écrire  , mais ce serait équivalent à
, mais ce serait équivalent à 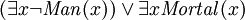 ("il ya quelque chose qui ne soit pas un homme, et / ou il existe quelque chose qui est mortel"), qui est généralement pas ce qui était prévu. De même, les affirmations peuvent être faites qu'un type est un sous-type d'un autre type, par exemple:
("il ya quelque chose qui ne soit pas un homme, et / ou il existe quelque chose qui est mortel"), qui est généralement pas ce qui était prévu. De même, les affirmations peuvent être faites qu'un type est un sous-type d'un autre type, par exemple: 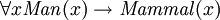 («pour tous
(«pour tous  , si
, si  est un homme, alors
est un homme, alors  est un mammifère ").
est un mammifère ").
Difficulté à finitude caractériser ou responsabilisation
Il r??sulte de ce Löwenheim-Skolem qu'il ne soit pas possible de caractériser la finitude ou de responsabilisation dans la logique du premier ordre. Par exemple, dans la logique du premier ordre on ne peut pas affirmer la propriété moins-limite supérieure pour des ensembles de nombres réels , qui stipule que tout, non vide délimité des nombres réels a une borne supérieure; Un logique du deuxième ordre est nécessaire pour cela.
Graphique accessibilité ne peut être exprimée
Plusieurs situations peuvent être modélisés comme un graphe de noeuds et de connexions dirigées (bords). Par exemple, la validation de nombreux systèmes nécessite montrant qu'un «mauvais» état ??????ne peut être atteint à partir d'un «bon» état, et ces interconnexions des Etats peut souvent être modélisé comme un graphe. Cependant, il peut être prouvé que la connectivité ne peut être pleinement exprimée dans la logique des prédicats. En d'autres termes, il n'y a pas de formule prédicat logique  et
et 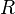 comme seul symbole de prédicat (d'arité 2) de telle sorte que
comme seul symbole de prédicat (d'arité 2) de telle sorte que 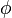 tient dans une interprétation
tient dans une interprétation 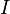 si et seulement si l'extension du
si et seulement si l'extension du 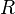 en
en 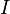 décrit un graphe connexe: qui est, graphes connexes ne peuvent pas être axiomatiser.
décrit un graphe connexe: qui est, graphes connexes ne peuvent pas être axiomatiser.
Notez que donnée une relation binaire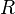 codant pour un graphe, on peut décrire
codant pour un graphe, on peut décrire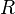 en termes d'une conjonction de formules du premier ordre, et d'écrire une formule
en termes d'une conjonction de formules du premier ordre, et d'écrire une formule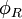 qui est satisfiable si et seulement si
qui est satisfiable si et seulement si est connecté.
est connecté.
Comparaison avec d'autres logiques
- Logique du premier ordre typé permet variables et des termes d'avoir différents types (ou sortes ). Si il ya seulement un nombre fini de types, cela ne diffère pas vraiment grand-chose de logique du premier ordre, car on peut décrire les types avec un nombre fini de prédicats unaires et quelques axiomes. Parfois, il ya un type spécial de ?? valeurs de vérité, auquel cas les formules sont seulement termes de type ??.
- Logique du premier ordre avec des conditions de domaine ajoute conditions de domaine (DC) à la logique du premier ordre classique, permettant la manipulation des fonctions partielles; ces conditions peuvent être prouvées "sur le côté" d'une manière similaire à des conditions de type exactitude de PVS. Il ajoute également si-alors-sinon de garder les définitions et les preuves gérables (ils sont devenus trop complexes sans eux).
- Le standard SMT-LIB définit un langage utilisé par de nombreux groupes de recherche pour les théories satisfiability modulo; la logique complète est basée sur FOL avec l'égalité, mais ajoute sortes (types), if-then-else pour les termes et formules (ITE () et si .. alors .. d'autre ..), un let construire pour les termes et formules ( laisser et flet), et un distincte construction déclarant un ensemble de valeurs cotées en tant que distincte. Ses connecteurs sont pas , implique , et , ou , xor , et ssi .
- Logique du deuxième ordre Faiblepermet la quantification sur des sous-ensembles finis.
- Logique du second ordre monadiquepermet la quantification sur des sous-ensembles, ou en d'autres termes plusunaireprédicats.
- Logique du deuxième ordre permet la quantification sur des sous-ensembles et des relations, ou en d'autres termes plus de tous les prédicats. Par exemple, le axiome de extensionnalité peut être indiqué dans la logique du deuxième ordre que x = y ??? def
 P ( P ( x ) ??? P ( y )). Les fortes sémantique de la logique du second ordre donnent ces phrases un sens beaucoup plus forte que la sémantique de premier ordre.
P ( P ( x ) ??? P ( y )). Les fortes sémantique de la logique du second ordre donnent ces phrases un sens beaucoup plus forte que la sémantique de premier ordre. - Ordre supérieur logiques permet la quantification sur les types plus élevés que de second ordre logiques permis. Ces types supérieurs comprennent les relations entre les relations, les fonctions de relations aux relations entre les relations, etc.
- Logique du premier ordre Intuitionistic utilise intuitionniste plutôt que le calcul propositionnel classique; par exemple, ¬¬?? ne doit pas être équivalente à ??. De m??me, logique floue de premier ordre sont des extensions de premier ordre de la logique floue propositionnelles plutôt que la logique classique.
- La logique modalea supplémentairesopérateurs modauxavec des significations qui peuvent être caractérisés de façon informelle, par exemple "il est nécessaire que ??" et "il est possible que ??".
- En prédicat monadique calculdes prédicats sont limités à avoir un seul argument.
- Logique infinitaire permet infiniment longues peines. Par exemple, on peut permettre une conjonction ou de disjonction d'une infinité de formules, ou quantification infiniment plus grand nombre de variables. Infiniment longues peines se posent dans les domaines des mathématiques, y compris la topologie et th??orie des mod??les.
- Logique du premier ordre avec des quantificateurs supplémentairesa de nouveaux quantificateursQx, ..., avec des significations telles que "il ya beaucoup dextelle que ... ". Voir aussi quantificateurs de branchement et lesquantificateurs pluriel deGeorge Boolos et d'autres.
- La logique des prédicats des définitions (PLD, ou D-logique) modifie FOL en ajoutant formellement définitions syntaxiques comme un type de valeur (en plus de formules et modalités); ces définitions peuvent être utilisés à l'intérieur des termes et formules.
- logique de l'Indépendance de l'environnementest caractérisé pardes quantificateurs de branchement, qui permettent d'exprimer indépendance entre variables quantifiées.
La plupart de ces logiques sont dans certaines extensions de sens de FOL: ils comprennent tous les quantificateurs et des opérateurs logiques de FOL avec les mêmes significations. Lindström a montré que FOL a pas d'extensions (autres qu'elle-même) qui satisfont à la fois le théorème de compacité et de la baisse théorème Löwenheim-Skolem. Une déclaration précise de théorème de Lindström nécessite quelques conditions techniques que la logique est supposé satisfaire; par exemple, en changeant les symboles d'une langue ne devrait faire aucune différence essentielle à laquelle phrases sont vraies.
Algebraizations
Trois moyens d'éliminer les variables quantifiées de FOL, et qui ne comportent pas de remplacer les quantificateurs avec d'autres opérateurs de liaison variables terme, sont connus:
- Algèbre cylindrique, parAlfred Tarski et ses collègues;
- Algèbre polyadique, parPaul Halmos;
- Logique de foncteur prédicat, principalement en raison deWillard Quine.
Cesalgèbres:
- Sont toutes les extensions propres de l'deux éléments algèbre de Boole, et sont doncréseaux;
- Faire pour FOL ceLindenbaum-Tarski algèbre fait pourla logique propositionnelle;
- Autoriser les résultats del'algèbre abstraite,algèbre universelle, etla théorie de l'ordre à être exercées sur FOL.
Tarski et Givant (1987) montrent que le fragment de FOL qui n'a pas de phrase atomique se trouvant dans le champ d'application de plus de trois quantificateurs, a le même pouvoir expressif que rapport alg??bre. ce fragment est d'un grand intérêt, car il suffit à l'arithmétique de Peano et plus la théorie des ensembles axiomatique , y compris le canonique ZFC. Ils prouvent aussi que FOL avec une primitive paire ordonnée est équivalent à une algèbre de relation avec deux paires commandées fonctions de projection.
Automatisation
Théorèmes de logique du premier ordre est l'un des sous-champs plus matures de démonstration automatique. La logique est suffisamment expressif pour permettre la spécification de problèmes arbitraires, souvent d'une manière raisonnablement naturelle et intuitive. D'autre part, il est encore semidecidable, et un certain nombre de sons et complètes calculs ont été développés, permettant systèmes entièrement automatisés. En 1965, J. Alan Robinson a réalisé une percée importante avec son approche de la résolution; pour prouver un théorème il tente de réfuter le théorème niée, d'une manière orientée vers un but, résultant dans une méthode beaucoup plus efficace pour prouver des théorèmes automatiquement dans FOL. Plus logiques expressives, comme d'ordre supérieur et de la logique modale, permettent l'expression pratique d'un large éventail de problèmes que la logique du premier ordre, mais théorèmes pour ces logiques est moins bien développés.
Une nouvelle technologie moderne et particulièrement perturbateur est que dessolveurs SMT, qui ajoutent l'arithmétique et le soutien des propositions pour les classes de puissantssolveurs SAT.