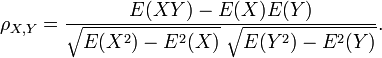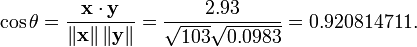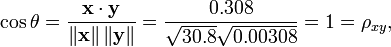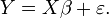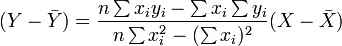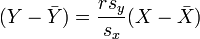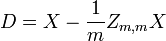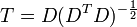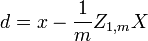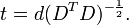Corr??lation

Saviez-vous ...

SOS croit que l'??ducation donne une meilleure chance dans la vie des enfants dans le monde en d??veloppement aussi. Parrainage d'enfants aide les enfants du monde en d??veloppement ?? apprendre aussi.

Cet article porte sur le coefficient de corr??lation entre deux variables. Le terme corr??lation peut aussi signifier la corr??lation crois??e des deux fonctions ou corr??lation d'??lectrons dans des syst??mes mol??culaires.

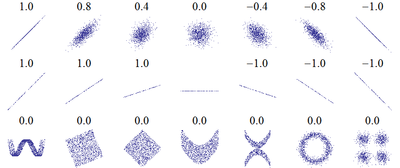
Plusieurs ensembles de (x, y) points, le coefficient de corr??lation x et y pour chaque ensemble. Notez que la corr??lation refl??te le caract??re bruyant et la direction d'une relation lin??aire (rang??e du haut), mais pas la pente de cette relation (au milieu), ni de nombreux aspects des relations non lin??aires (en bas). NB: le chiffre dans le centre dispose d'une pente de 0 mais dans ce cas, le coefficient de corr??lation est d??finie parce que la variance de Y est z??ro.

Dans la th??orie des probabilit??s et statistiques , corr??lation, (souvent mesur??e comme un coefficient de corr??lation), indique la force et la direction d'une relation lin??aire entre deux variables al??atoires . Dans l'usage statistique g??n??ral, la corr??lation ou co-relation d??signe le d??part de deux variables de l'ind??pendance. Dans ce sens large, il existe plusieurs coefficients, mesurant le degr?? de corr??lation, adapt??e ?? la nature des donn??es.

Un certain nombre de coefficients diff??rents sont utilis??s pour diff??rentes situations. Le plus connu est le Pearson coefficient de corr??lation produit-moment, qui est obtenu en divisant le covariance des deux variables par le produit de leurs ??carts types . Malgr?? son nom, il a ??t?? introduit par Francis Galton.

Le coefficient produit-moment de Pearson

Propri??t??s math??matiques

Le coefficient de corr??lation ρ _{X, Y} entre deux variables al??atoires X et Y avec valeurs attendues μ _X et _Y μ et ??carts types σ _X et _Y σ est d??finie comme:

$\ Rho_ {X, Y} = {\ mathrm {} cov (X, Y) \ over \ sigma_X \ sigma_Y} = {E ((X \ mu_X) (Y \ mu_Y)) \ over \ sigma_X \ sigma_Y} ,$

o?? E est le op??rateur de valeur attendue et cov moyens covariance. Depuis μ _X = E (X), σ _X ² = E (X ²⁾ - ² E (X) et de m??me pour Y, on peut aussi ??crire

$\ Rho_ {X, Y} = \ frac {E (XY) -E (X) E (Y)} {\ sqrt {E (X ^ 2) -E ^ 2 (X)} ~ \ sqrt {E (Y ^ 2) ^ 2 -E (Y)}}.$

La corr??lation est d??finie que si les deux des ??carts types sont limit??es et deux d'entre eux sont non nuls. Ce est un corollaire de l' in??galit?? de Cauchy-Schwarz que la corr??lation ne peut pas d??passer 1 en valeur absolue .

La corr??lation est 1 dans le cas d'une relation lin??aire croissante, -1 dans le cas d'une relation lin??aire d??croissante, et une valeur entre dans tous les autres cas, ce qui indique le degr?? de d??pendance lin??aire entre les variables. Plus le coefficient est soit -1 ou 1, plus la corr??lation entre les variables.

Si les variables sont ind??pendant puis la corr??lation est ??gal ?? 0, mais le contraire ne est pas vrai, parce que le coefficient de corr??lation ne d??tecte que des d??pendances lin??aires entre les deux variables. Voici un exemple: Supposons que la variable al??atoire X est r??parti uniform??ment sur l'intervalle -1 ?? 1, et Y = X ^2. Alors Y est compl??tement d??termin??e par X, de sorte que X et Y d??pendent, mais leur corr??lation est ??gal ?? z??ro; ils sont d??corr??l??es. Toutefois, dans le cas particulier o?? X et Y repr??sentent conjointement normale, non corr??lation est ??quivalent ?? l'ind??pendance.

Une corr??lation entre deux variables est dilu?? en pr??sence d'erreur de mesure autour des estimations de l'un ou les deux variables, auquel cas disattenuation fournit un coefficient plus pr??cis.

Interpr??tation g??om??trique de corr??lation

Le coefficient de corr??lation peut ??galement ??tre consid??r?? comme le cosinus de l' angle entre les deux vecteurs d'??chantillons tir??s des deux variables al??atoires.

Attention: Cette m??thode fonctionne uniquement avec des donn??es centr??es, ce est ?? dire, les donn??es qui ont ??t?? d??cal??es de la moyenne de l'??chantillon de mani??re ?? avoir une moyenne de z??ro. Certains praticiens pr??f??rent une (non-conforme Pearson) coefficient de corr??lation d??centr??. Voir l'exemple ci-dessous pour une comparaison.

A titre d'exemple, supposons que cinq pays sont trouv??s d'avoir des produits nationaux bruts de 1, 2, 3, 5 et 8 milliards de dollars, respectivement. Supposons que ces cinq m??mes pays (dans le m??me ordre) sont trouv??s d'avoir 11%, 12%, 13%, 15%, et 18% la pauvret??. Ensuite, laissez x et y ??tre command??s vecteurs 5 ??l??ments contenant les donn??es ci-dessus: x = (1, 2, 3, 5, 8) et y = (0,11, 0,12, 0,13, 0,15, 0,18).

Par la proc??dure habituelle pour trouver l'angle entre deux vecteurs (voir point produit), le coefficient de corr??lation est d??centr??:

$\ Cos \ theta = \ frac {\ gras {x} \ cdot \ gras {y}} {\ left \ | \ gras {x} \ right \ | \ left \ | \ gras {y} \ right \ |} = \ frac {2,93} {\ sqrt {103} \ sqrt {}} = 0,0983 0,920814711.$

Notez que les donn??es ci-dessus ont ??t?? d??lib??r??ment choisis pour ??tre parfaitement corr??l??s: y = 0,10 + 0,01 x. Le coefficient de corr??lation de Pearson doit donc ??tre exactement un. Centrage des donn??es (d??calage x par E (x) = 3,8 et y par E (y) = 0,138) rendements x = (-2,8, -1,8, -0,8, 1,2, 4,2) et y = (-0,028, -0,018, -0,008, 0,012, 0,042), ?? partir de laquelle

$\ Cos \ theta = \ frac {\ gras {x} \ cdot \ gras {y}} {\ left \ | \ gras {x} \ right \ | \ left \ | \ gras {y} \ right \ |} = \ frac {0,308} {\ sqrt {30,8} \ sqrt {}} = 0,00308 1 = \ {xy} rho_,$

comme pr??vu.

Motivation pour la forme du coefficient de corr??lation

Une autre motivation pour la corr??lation vient d'inspecter la m??thode d'une simple r??gression lin??aire . Comme ci-dessus, X est le vecteur des variables ind??pendantes, 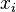$x_i$ Et Y des variables d??pendantes, 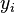$y_i$ Et une relation lin??aire simple entre X et Y est recherch??e, par une m??thode des moindres carr??s sur l'estimation de Y:

$\ Y = X \ beta + \ varepsilon. \,$

Ensuite, l'??quation de la droite des moindres carr??s peut ??tre d??riv?? ?? ??tre de la forme:

$(Y - \ bar {Y}) = \ frac {n \ sum x_iy_i- \ sum x_i \ sum y_i} {n \ sum x_i ^ 2 - (\ sum x_i) ^ 2} (X - \ bar {X})$

qui peuvent ??tre r??organis??s sous la forme:

$(Y - \ bar {Y}) = \ frac {} {r s_y s_x} (X \ bar {X})$

o?? r a la forme famili??re mentionn?? ci-dessus: 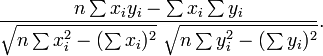$\ Frac {n \ sum x_iy_i- \ sum x_i \ sum y_i} {\ sqrt {n \ sum x_i ^ 2 - (\ sum x_i) ^ 2} ~ \ sqrt {n \ sum y_i ^ 2 - (\ sum y_i) ^ 2}}.$

Interpr??tation de la taille d'une corr??lation

Corr??lation	N??gatif	Positif
Petit	-0,3 ?? -0,1	0,1 ?? 0,3
Moyen	-0,5 ?? -0,3	0,3 ?? 0,5
Grand	-1,0 ?? -0,5	0,5 ?? 1,0

Plusieurs auteurs ont propos?? des lignes directrices pour l'interpr??tation d'un coefficient de corr??lation. Cohen (1988), par exemple, a sugg??r?? les interpr??tations suivantes des corr??lations dans la recherche psychologique, dans le tableau sur la droite.

Comme Cohen lui-m??me a observ??, toutefois, tous ces crit??res sont en quelque sorte arbitraire et ne doivent pas ??tre observ??s de mani??re trop stricte. En effet, l'interpr??tation d'un coefficient de corr??lation d??pend du contexte et des objectifs. Une corr??lation de 0,9 peut ??tre tr??s faible si l'on v??rifie une loi physique en utilisant des instruments de haute qualit??, mais peut ??tre consid??r?? comme tr??s ??lev?? dans les sciences sociales, o?? il peut y avoir une plus grande contribution des facteurs de complication.

Le long de cette veine, il est important de rappeler que ??grande?? et ??petite?? ne devrait pas ??tre pris comme synonymes de ??bon?? et ??mauvais?? en termes de d??terminer qu'une corr??lation est d'une certaine taille. Par exemple, une corr??lation de 1,0 ou -1,0 indique que les deux variables sont analys??es calibrage modulo ??quivalent. Scientifiquement, cela signifie plus fr??quemment le r??sultat trivial qu'un fracassant une. Par exemple, consid??rez la d??couverte d'une corr??lation de 1,0 entre le nombre de pieds de hauteur un groupe de personnes sont et le nombre de pouces du fond de leurs pieds au dessus de leurs t??tes.

Les coefficients de corr??lation non param??triques

Le coefficient de corr??lation de Pearson est un statistique param??trique et lorsque les distributions ne sont pas normaux, il peut ??tre moins utile que des m??thodes de corr??lation non param??triques, tels que Chi-carr??, Pointez corr??lation bis??riale, La ρ de Spearman et Le τ de Kendall. Ils sont un peu moins puissant que les m??thodes param??triques si les hypoth??ses sous-jacentes ce dernier sont remplies, mais sont moins susceptibles de donner des r??sultats fauss??s lorsque les hypoth??ses ??chouent.

Autres mesures de d??pendance entre les variables al??atoires

Pour obtenir une mesure de plus de d??pendances g??n??rales dans les donn??es (??galement non lin??aire), il est pr??f??rable d'utiliser la rapport de corr??lation qui est capable de d??tecter presque toute d??pendance fonctionnelle, ou la bas??e sur l'entropie information mutuelle / corr??lation totale qui est capable de d??tecter des d??pendances m??me plus g??n??rales. Ces derniers sont parfois appel??s mesures de corr??lation multi-moments, par rapport ?? ceux qui consid??rent seulement 2e instant (par paires ou quadratique) la d??pendance.

Le polychoric corr??lation est une autre corr??lation appliqu??e aux donn??es ordinales qui vise ?? estimer la corr??lation entre les variables latentes th??oris??s.

Copules et corr??lation

L'information fournie par un coefficient de corr??lation ne est pas suffisant pour d??finir la structure de d??pendance entre les variables al??atoires; pour capturer pleinement, nous devons envisager une copule entre eux. Le coefficient de corr??lation d??finit compl??tement la structure de d??pendance que dans des cas tr??s particuliers, par exemple lorsque le fonctions de r??partition sont les distributions normales multivari??es. Dans le cas des distributions elliptiques elle caract??rise les (hyper) ellipses de densit?? ??gale, cependant, il ne caract??rise pas compl??tement la structure de d??pendance (par exemple, les degr??s de libert?? de l'un multivari??e t de distribution d??terminent le niveau de d??pendance de queue).

matrices de corr??lation

La matrice de corr??lation des variables al??atoires X ₁ n, ..., X _n est la matrice n ?? n dont i, j est entr??e corr (X _i, X _j). Si les mesures de corr??lation sont utilis??s coefficients produit-moment, la matrice de corr??lation est le m??me que le matrice de covariance des variables al??atoires normalis??es X _i / SD (X _i) pour i = 1, ..., n. Par cons??quent, il est n??cessairement un matrice semi-d??finie positive.

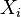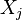La matrice de corr??lation est sym??trique car la corr??lation entre $X_i$ et $X_j$ est la m??me que la corr??lation entre 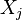$X_j$ et $X_i$ .

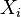Retrait corr??lation

Il est toujours possible de supprimer la corr??lation entre les variables al??atoires de moyenne nulle avec une transformation lin??aire, m??me si la relation entre les variables est non lin??aire. Supposons un vecteur de variables al??atoires n est ??chantillonn?? m fois. Soit X une matrice o?? 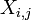$X_ {i, j}$ est le j e variable de l'??chantillon i. Laisser 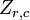$Z_ {r, c}$ ??tre un r par la matrice de c avec chaque ??l??ment 1. Alors D est les donn??es transform??es de sorte que chaque variable al??atoire a moyenne nulle, et T est les donn??es transform??es de fa??on toutes les variables ont une moyenne nulle, de variance unit??, et de z??ro corr??lation avec toutes les autres variables. Les variables transform??es seront pas corr??l??es, m??me si elles peuvent ne pas ??tre ind??pendante.

$D = X - \ frac {1} {m} Z_ {m, m} X$

$T = D (D ^ T D) ^ {- \ frac {1} {2}}$

o?? un exposant de -1/2 repr??sente la racine carr??e de la matrice inverse d'une matrice. La matrice de covariance de T sera la matrice identit??. Si un nouvel ??chantillon de donn??es x est un vecteur ligne de n ??l??ments, la m??me transformation peut ??tre appliqu??e ?? x pour obtenir les vecteurs transform??s D et T:

$d = x - \ frac {1} {m} Z_ {1, m} X$

$t = d (D ^ T D) ^ {- \ frac {1} {2}}.$

Id??es fausses sur la corr??lation

Corr??lation et causalit??

Le dicton classique qui " corr??lation ne implique pas causalit?? "signifie que la corr??lation ne peut ??tre valablement utilis??e pour d??duire une relation de causalit?? entre les variables. Cette maxime ne devrait pas ??tre interpr??t?? comme signifiant que les corr??lations ne peuvent pas r??v??ler des relations causales. Toutefois, les causes sous-jacentes de la corr??lation, le cas ??ch??ant, peut ??tre indirecte et inconnus. Par cons??quent, l'??tablissement d'une corr??lation entre deux variables ne est pas une condition suffisante pour ??tablir une relation causale (dans les deux sens).

Voici un exemple simple: temps chaud peut provoquer les achats de criminalit?? et de glaces. Par cons??quent la criminalit?? est en corr??lation avec les achats glaces. Mais le crime ne provoque pas achats glaces et les achats glaces ne causent pas de crime.

Une corr??lation entre l'??ge et la hauteur chez les enfants est assez causalement transparent, mais une corr??lation entre l'humeur et la sant?? dans la population est moins. Am??lioration de l'humeur ne conduisent ?? une meilleure sant??? Ou est bonne avance de sant?? ?? la bonne humeur? Ou ne un autre facteur sous-tendent les deux? Ou est-ce une pure co??ncidence? En d'autres termes, une corr??lation peut ??tre consid??r?? comme une preuve d'un lien de causalit?? possible, mais ne peut pas indiquer quelle est la relation de cause ?? effet, le cas ??ch??ant, pourrait ??tre.

Corr??lation et lin??arit??

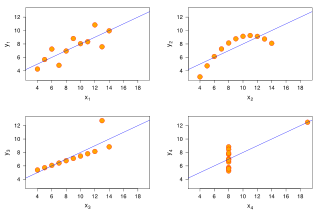
Quatre ensembles de donn??es avec le m??me corr??lation de 0,81

Bien que la corr??lation de Pearson indique la force d'une relation lin??aire entre deux variables, sa valeur seule peut ne pas suffire pour ??valuer cette relation, en particulier dans le cas o?? l'hypoth??se de normalit?? est incorrect.

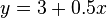L'image sur la droite affiche nuages de points Quartet d'Anscombe, un ensemble de quatre paires diff??rentes de variables cr????es par Francis Anscombe. Les quatre $y$ variables ont la m??me moyenne (7,5), l'??cart-type (4,12), la corr??lation (0,81) et la ligne de r??gression ( $y = 3 + 0.5x$ ). Cependant, comme on peut le voir sur les emplacements, la distribution des variables est tr??s diff??rente. La premi??re (en haut ?? gauche) semble ??tre distribu?? normalement, et correspond ?? ce que l'on pourrait se attendre lorsque l'on consid??re deux variables corr??l??es et apr??s l'hypoth??se de normalit??. Le second (en haut ?? droite) ne est pas distribu??e normalement; alors une relation ??vidente entre les deux variables peut ??tre observ??, il ne est pas lin??aire, et le coefficient de corr??lation de Pearson ne est pas pertinent. Dans le troisi??me cas (en bas ?? gauche), la relation lin??aire est parfait, sauf une aberrante qui exerce une influence suffisante pour abaisser le coefficient de corr??lation de 1 ?? 0,81. Enfin, l'exemple quatri??me (en bas ?? droite) montre un autre exemple o?? une valeur aberrante est suffisante pour produire un coefficient de corr??lation ??lev??, m??me si la relation entre les deux variables ne est pas lin??aire.

Ces exemples montrent que le coefficient de corr??lation, comme une statistique sommaire, ne peut pas remplacer l'examen individuel des donn??es.

Le calcul de corr??lation avec pr??cision en une seule passe

L'algorithme suivant (en pseudo) calculera Corr??lation de Pearson avec une bonne stabilit?? num??rique.

 sum_sq_x = 0 = 0 sum_sq_y sum_coproduct = 0 mean_x = x [1] mean_y = y [1] for i in 2 ?? N: balayage = (i - 1,0) / i delta_x = x [i] - mean_x delta_y = y [i ] - mean_y sum_sq_x + = delta_x * * delta_x balayage sum_sq_y + = delta_y * * delta_y balayage sum_coproduct + = delta_x * * delta_y balayage mean_x + = delta_x / i mean_y + = delta_y / i pop_sd_x = sqrt (sum_sq_x / N) pop_sd_y = sqrt (sum_sq_y / N) = cov_x_y sum_coproduct / N = corr??lation cov_x_y / (pop_sd_x * pop_sd_y)

R??cup??r?? ?? partir de " http://en.wikipedia.org/w/index.php?title=Correlation_and_dependence&oldid=199055311 "